指向思维发展的小学生“数学微演讲”

朱向明

【摘   要】数学微演讲作为数学综合实践活动的一种形式，其重要价值之一在于促进儿童思维的发展：在数学阅读中培养思维的广阔性和深刻性，在数学写作中培养思维的灵活性和批判性，在口语表达中培养思维的敏捷性和创新性。

【关键词】数学微演讲;思维品质;数学阅读;数学写作;口语表达

数学微演讲是数学综合实践活动的一种创新形式。数学微演讲往往起始于数学阅读——信息输入，准备体现在数学写作——信息加工，结果呈现为数学表达——信息输出。提高数学微演讲水平的过程，就是提高思维水平的过程。广阔性、深刻性、灵活性、批判性、敏捷性、创新性等思维品质的发展贯穿于数学微演讲始终。

一、在数学阅读中培养思维的广阔性和深刻性

数学阅读是数学学习的重要途径，尤其提倡在独立自主状态下，学生选择感兴趣的数学内容进行阅读。数学微演讲的起点在数学阅读，阅读的过程是信息输入的过程，这一过程中既能丰富一定“量”的积累，也有助于演讲者围绕某一问题进行“深度品读”。

（一）在博观约取中培养思维的广阔性

数学思维的广阔性是指学生能够多角度概括、表征、分析和解决现实情境中的数学问题，能够将数学方法广泛应用到现实情境和其他相关的数学问题中的能力。[1]阅读是广阔性思维品质形成的基础，有主题的数学微演讲，有助于学生围绕某一专题进行广博的主题性阅读。

例如，教学“圆”这一单元，教师引导学生围绕“圆”这一主题，在自主搜集材料广泛阅读的基础上，从不同角度寻找主题作为自己微演讲的内容，有助于学生在保持充足兴趣的前提下增加阅读量。

在准备的过程中，学生可以细致梳理“圆”的悠久历史，感受“圆”中的数学文化;可以看到“π的前世今生”;可以发现“无处不在的圆”;甚至可以结合课本上高频出现的“正方形内最大的圆”，想到如何去研究“方与圆”的关系。这样在广泛阅读资料的基础上确定演讲主题，选择演讲的素材，学生对丰富的材料进行概括、表征、分析，其思维的广阔性得到了极大的培养和训练。

（二）在品读追问中培养思维的深刻性

数学思维的深刻性是指学生能够透过事物的表面现象，认识事物的本质以及事物间的本质联系，反映思维活动的抽象和逻辑推理水平。[2]对于小学生而言，透过现象看本质的要求偏高，教师可以借助数学微演讲，在对某一问题的品读追问中让学生体会知识间的本质联系，从而提升思维的深刻性。

还以前文提到的“正方形内最大的圆”为例，在单元复习中，教师引导学生以“方与圆”为微演讲的主题，将教材中的相关图形进行整理并品读。学生由简单的方与圆的组合，提出新的问题：“在正方形中，还能设计出怎样的图形，使涂色面积不变？”由方与圆的简单变式，提出新的问题：“怎样在长方形内画最大的圆，圆的面积与长方形的面积有怎样的关系？”由方与圆的重复变式，提出新的问题：“在正方形内还可以画出多少个同样大的圆？剪下的铁皮面积相等吗？剪下的圆的个数有什么特点？……”学生的思维在对图形观察、计算、比较与追问中逐渐走向深刻。

二、在数学写作中培养思维的灵活性和批判性

如果说数学阅读是在信息输入的同时，对数学信息进行简单的“粗加工”，那么数学写作则是对数学信息的精细加工。学生通过加工阅读材料，形成演讲文本初稿，然后在对初稿反复修改打磨中，对知识的理解逐步深入，对方法的运用更加灵活，对问题的认识更加全面，思维的灵活性和批判性得以培养和训练。

（一）在形成初稿中培养思维的灵活性

数学思维的灵活性是指数学思维过程的灵活程度。[3]学生写演讲稿就是熟练运用数学语言灵活表达自己想法的过程。在这一过程中，学生能否正确、合理地使用数学语言，正是其思维灵活性的表现。

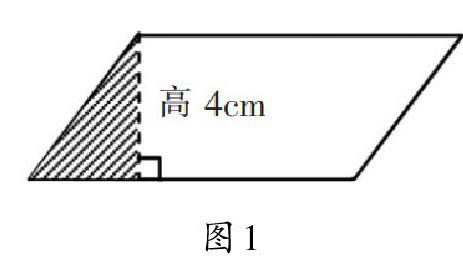
以常规的微演讲——“好题我讲”为例。有学生选择了这一问题：在平行四边形中（如图1），阴影部分的面积是6平方厘米，平行四边形底是三角形底的3倍。空白部分的面积是多少平方厘米？学生一般会选择常规解决办法：先求三角形的底，再求平行四边形的底，最后根据梯形面积公式求出空白部分面积。在对图形整体观察分析的基础上，有学生找到新的解题思路：根据所给的“平行四边形底是三角形底的3倍”这一条件在图中分一分、画一画，发现空白部分的面积就是阴影部分面积的5倍，从而直接解决问题，形成了“根据关系巧解题”的演讲初稿。在上述初稿形成过程中，学生运用所学的数学语言——图形概念、公式、关系，表达自己对问题的理解，锻炼了思维的灵活性。

（二）在修改润色中培养思维的批判性

数学思维的批判性是指学生对数学思维过程和思维结果的反思分析改进的特征。[4]学生在形成初稿后一般会反复审读，不断修改润色，通过自我提问、自我完善等方式形成自认为最佳的演讲稿，这一过程是对资料、对自我不断反思与批判的过程。

如，在上述“根据关系巧解题”演讲初稿的基础上，可以将初稿中的一道题讲解，进一步修改为一类题的讲解。初稿作为其修改和润色的对象，通过确认“根据关系求面积”方法引发思考：还有哪些图形的面积可以用這样的方法来解答？学生在分别解答这几个问题后，对解答方法进行总结提炼，从而实现了从一道题到一类题的跨越。这样的跨越，正是源自学生对自己解答方法和思路的主动监控、反思和调整，源自学生的自我追问质疑和总结完善，而学生的批判性思维也在这个跨越过程中得到了发展。

三、在口语表达中培养思维的敏捷性和创新性

思维和语言密不可分。在演讲稿修改完成后，需要通过“演讲”将内化的思维用语言外化出来，这时，语言不仅是交际的工具，更是思维的“物质外壳”。具体表现在运用数学语言将问题或故事“讲流畅”，以此培养思维的敏捷性，进而“讲生动”，以此培养思维的创新性。

（一）在流畅“演讲”中培养思维的敏捷性

思维的敏捷性，是指思维过程的速度或迅速程度。[5]微演讲与写演讲稿的不同在于要把修改后的演讲稿流利地讲出来。这需要学生能够准确、迅速地提取演讲稿中的数学信息，将演讲稿中的数字、符号以及与文字相结合的书面语言转化为面向听众的口头语言。在数学语言与演讲语言互译的过程中，保持流利表达。而这一过程正是学生思维敏捷性的体现。

（二）在生动“演讲”中培养思维的创新性

小学生思维品质的创新性，更多体现在独创性和新颖性上，它不是指创造出新思想、新方法，而是其有别于他人或自己曾经的思考，具有一定新颖成分的思维品质。演讲的目的是以生动形象的语言及形式吸引听众，使其接受自己的观点和思想。数学微演讲仅停留在讲清晰、讲流畅的层面是不够的，而应在所写稿件、PPT制作、视频录制、语言运用等方面精益求精，力求生动有趣。而这真正体现了演讲者的智慧，是有别于他人或自己任何一次演讲的独创性所在。

数学微演讲作为综合实践活动的新形式，是打开儿童认知、促进儿童思维品质高质量发展的数学学习方式。在实践中，我们真切地感受到儿童思维品质获得的实实在在的提升，这正是我们开展数学微演讲的初心所在！

参考文献：

[1][2][3][4]冯回祥.思维方法与数学教学[M].武汉：华中科技大学出版社，2018.

[5]朱智贤，林崇德.思维发展心理学[M].北京：北京师范大学出版社，1986.

（江苏省苏州高新区实验小学校   215011）