矩阵奇异值不等式的一些广义结果

杨 巍， 张 峰

（1.广西工业职业技术学院基础教学部，广西南宁 530001；2.东北林业大学理学院，黑龙江哈尔滨 150040）

1 引言

在本文中，我们记Mn为n 阶复矩阵的全体，I为Mn上的单位矩阵.对于任意的A∈Mn，记s（A） 为A的奇异值的集合，即s（A）= {s1（A），…，sn（A）}，其中si（A） 为A的奇异值，且s1（A）≥ … ≥ sn（A）；对于任意的自共轭矩阵A∈Mn，记λ（A）为A的特征值的集合，即λ（A）= {λ1（A），…，λn（A）}，其中λi（A）为A的奇异值，A≥0 表示A是半正定矩阵，如果I-A*A≥0 ，则称A是可压缩的.可以证明，A是压缩矩阵当且仅当s1（A）≤1 .

其中A，B∈Mn是半正定矩阵，m≥2 是一个正整数.著名的Lieb-Thirring 不等式[9]说明了对于半正定矩阵A，B以及正整数m，都有tr（AB）m≤trAmBm，当m≥2 时 ，Lieb-Thirring 不等式是不等式（2）的一个特殊情况.以上都说明了压缩矩阵的重要性.

下面介绍向量优超的定义.假设一个实向量x=（x1，x2，…，xn）∈Rn，重新排列顺序使得x[1]≥x[2]≥ …≥x[n].对于x=（x1，x2，…，xn），y=（y1，y2，…，yn）∈Rn，如果

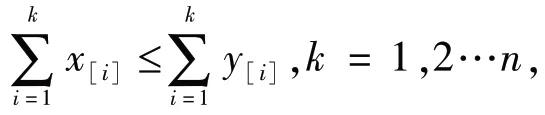
正如文献［4］中所说，这些方法似乎很难推广到更多矩阵，本文的目的向量就是提供这样一种扩展，将上述结果与压缩矩阵相结合，得到了

进一步，在（6）中，给出了AiCi=CiAi，AiDi=DiAi这个条件的必要性.

2 引理

在证明主要结果之前，我们需要一些引理.

引理 2.1 （Exercise1.5.1[5]）.令Ai∈ Mn（i=1，2，…k） 是半正定矩阵，则有

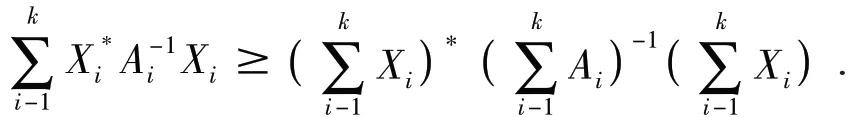
引理 2.2 （Theorem4.2.3[5]）令Ai∈ Mn（i=1，2，…k） 是半正定矩阵，对于0 ≤r≤1 ，则有

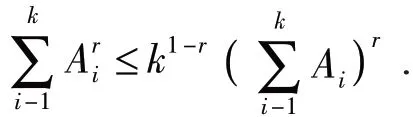
引理 2.3 （Corollary3.2.3[6]）令A，B，C，D∈Mn是半正定矩阵，且A≤C，B≤D，对于任意j=1，2，…n ，有λj（AB） ≤λj（CD） .

值得注意的是，即使A，B是正定的，如果特征值被奇异值代替，引理2.3中的不等式也不成立.

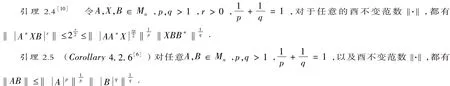
引理 2.6 （Theorem3.4.5[6]）对于任意Ai∈ Mn（i=1，2，…，k） ，都有

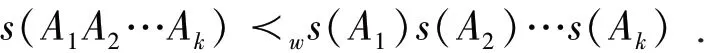
引理 2.7 （Example2.3.5[6]）对于任意的酉不变范数‖·‖ ，以及任意A，B∈Mn，p≥1 ，‖A‖≤‖B‖⇒‖A‖p≤‖B‖p.

3 主要结果

定理3.1 设Ai∈ Mn（i=1，2） 为半正定矩阵，C1，D1∈ Mn是压缩矩阵，则对于任意的酉不变范数‖·‖，

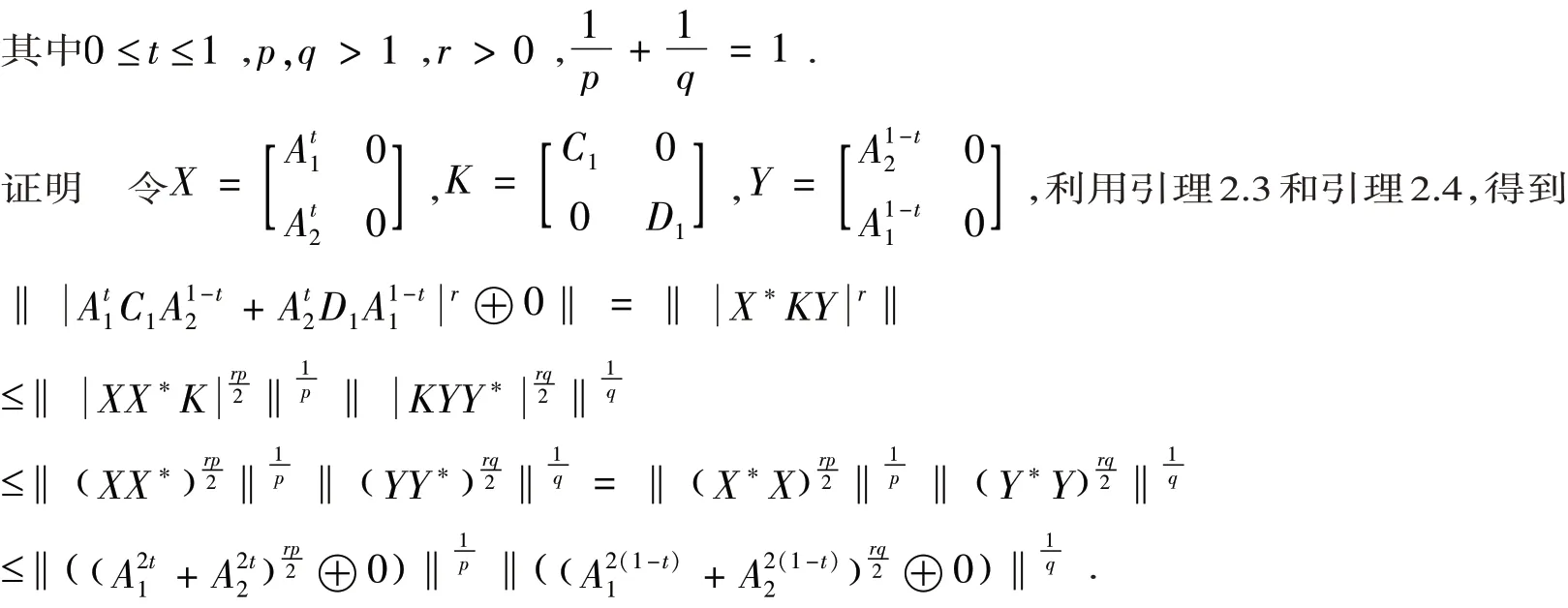
再根据引理2.2，得到

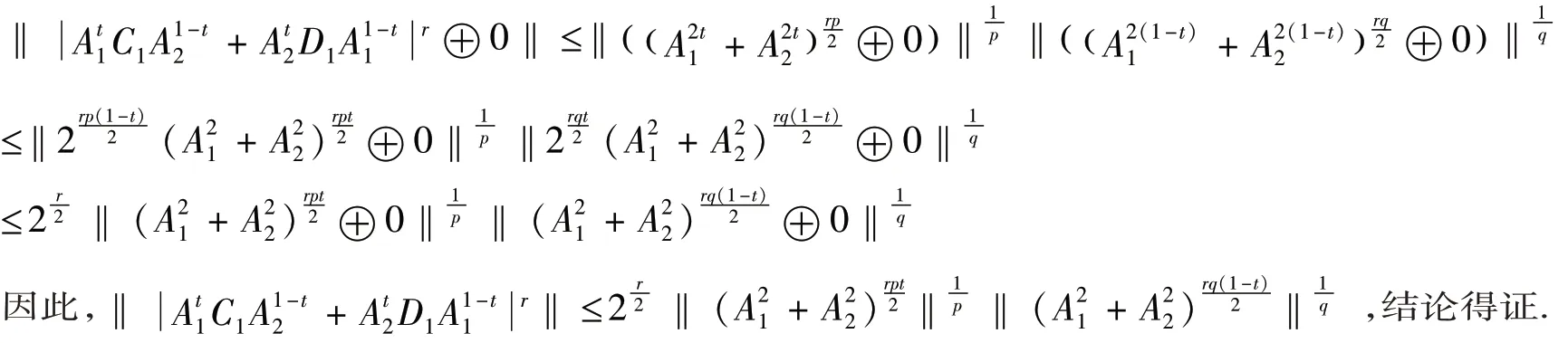
注释3.1 在定理3.1中令p=q=2 ，则有

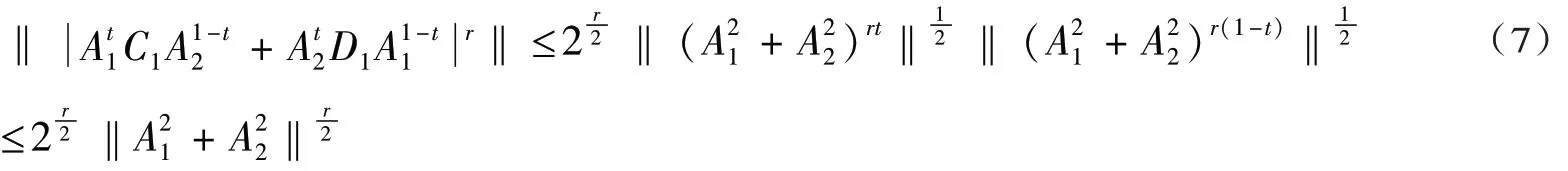
我们观察到不等式（3）是不等式（7）的特例，另一方面，得到下面的不等式成立：

定理3.2 设Ai∈ Mn（i=1，2，…，k） 为半正定矩阵，Ci，Di∈ Mn（i=1，2，…，k） 是压缩矩阵，则对于任意的酉不变范数‖·‖，都有

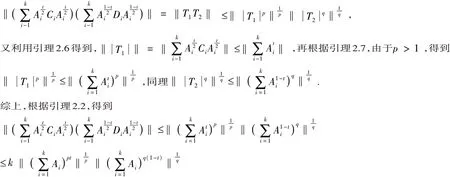
结论得证.

注释 3.2 利用不等式（4）和（9），得到

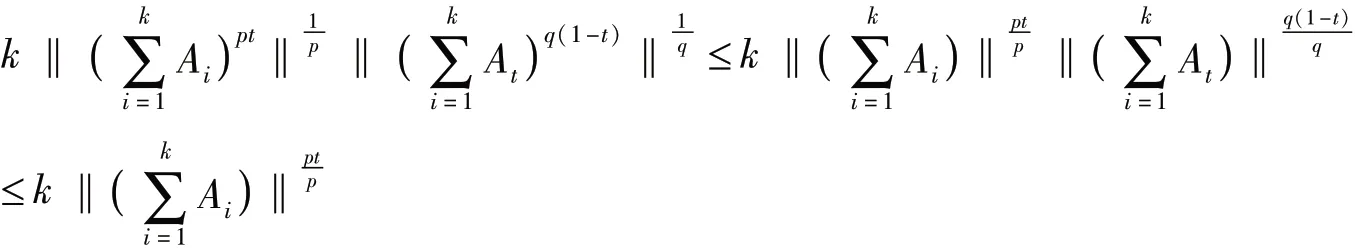
因此不等式（9）是（4）的改进，而这些结果都是（5）的扩展.

定理 3.3 设Ai∈ Mn（i=1，2，…，k） 为半正定矩阵，Ci，Di∈ Mn（i=1，2，…，k） 是压缩矩阵，满足AiCi=CiAi，AiDi=DiAi，则对于任意的0 ≤t≤1 ，都有

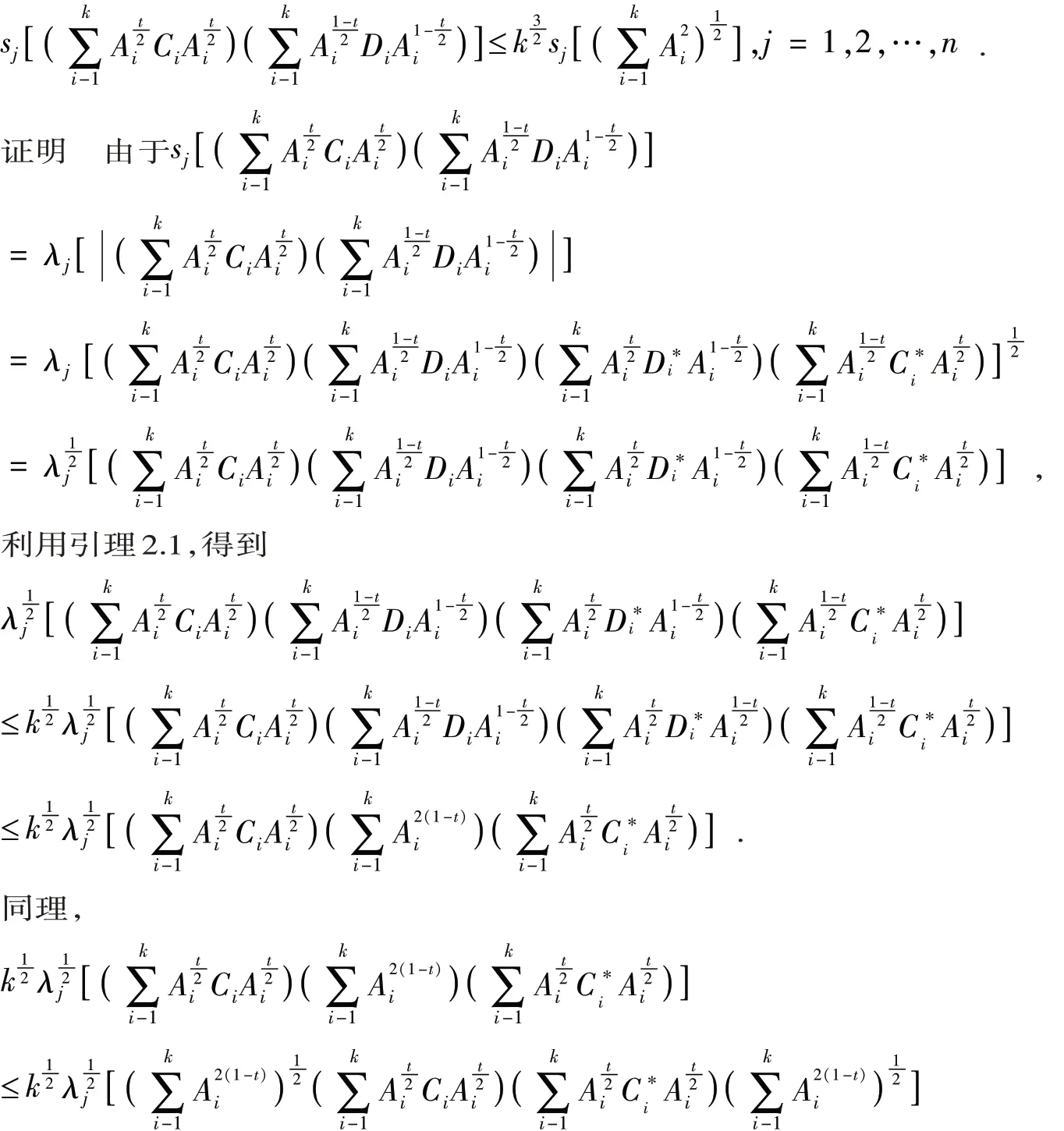
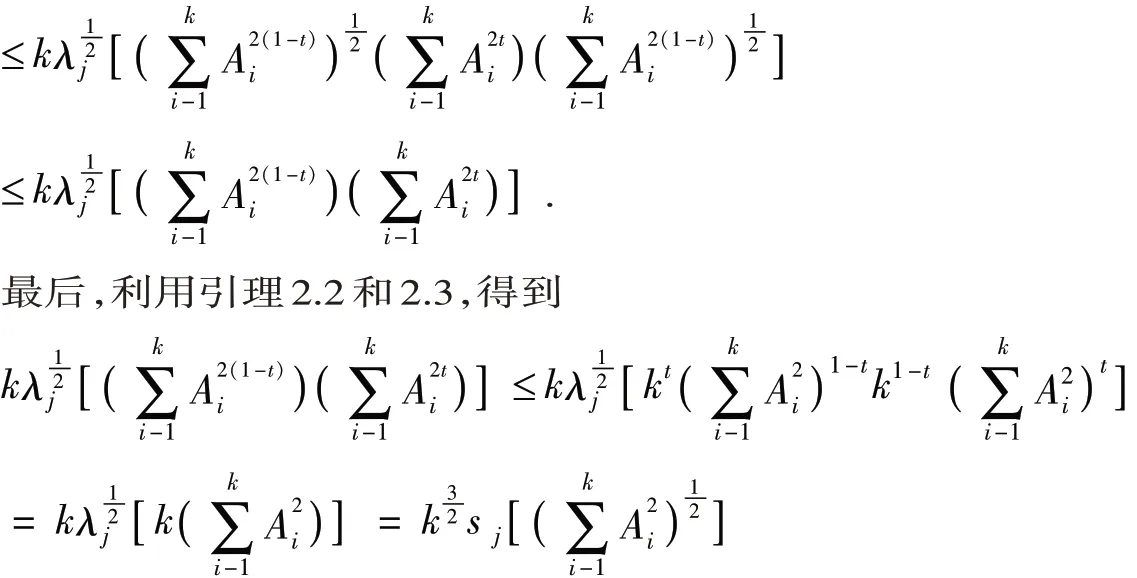
结论得证.

注释3.3 举例证明的必要性AiCi=CiAi，AiDi=DiAi.

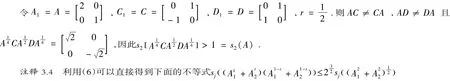
这个结果正是（4）的一个结论.