本征边界积分方程法模拟含流体粒子固体的性能

周吉成， 和东宏， 马 杭

(1. 上海大学上海市应用数学和力学研究所， 上海200072; 2. 上海大学理学院， 上海200444)

自然界中的许多材料， 如生物组织、饱和岩土、胶体材料、发泡塑料以及烧结陶瓷等通常都是流体与固体材料的复合体. 在这类含流体夹杂的弹性介质中， 流体粒子与基体之间存在复杂的相互作用， 其形状、体积分数和内压等都会对材料的有效力学性能产生影响. 显然， 这类材料的力学行为不同于含有固体粒子的材料. 近年来流体粒子对材料宏观有效性能影响规律的研究受到力学及复合材料研究者的关注[1-3].

对于夹杂粒子和非均质体的研究， 从1957 年Eshelby[4]创造性地提出等效夹杂理论后获得快速发展， 出现了大量对夹杂物和非均质体的研究[5-6]， 以及基于Eshelby 等效夹杂和本征应变解的各种理论分析[7-8]和数值计算[9]的研究. 在各种物理问题中， 本征应变解可适用于非协调热应变、相变、塑性应变以及残余应力的固有应变[10]等问题. 通过对Eshelby等效夹杂物的替换， 本征应变还可用来处理固体基体中的异质体如夹杂粒子、孔洞[11]等问题. Eshelby 等效夹杂理论在材料科学、力学、物理、工程等问题中均有广泛的应用. 近年来， 通过将边界积分方程与Eshelby 等效夹杂理论相结合， 已有研究者提出了本征应变边界积分方程的计算模型， 并成功地对含有大量固体粒子的固体进行了二维和三维数值模拟[12-13].

本工作将Eshelby 本征应变和等效夹杂理论与边界积分方程相结合， 提出了含大量流体粒子固体的本征应变边界积分方程的计算模型及迭代算法， 拓宽了模型的应用范围. 通过数值算例， 验证了计算模型的正确性和计算方法的可行性， 讨论了材料参数如流体粒子分布、孔隙率及压缩系数等对含流体粒子固体材料整体性能的影响.

1 计算模型

1.1 本征应变形式的边界积分方程

在本模型中， Ω 为求解域即固体基体， 其外边界为Γ; 基体中流体粒子总数NI所在的区域为 ΩI(I =1，2···，NI)， 其边界即粒子与基体的界面 ΓI(ΓI= ΩI∩Ω). 对于问题的求解域Ω，位移和应力边界积分方程[9，12-13]分别为

式中:

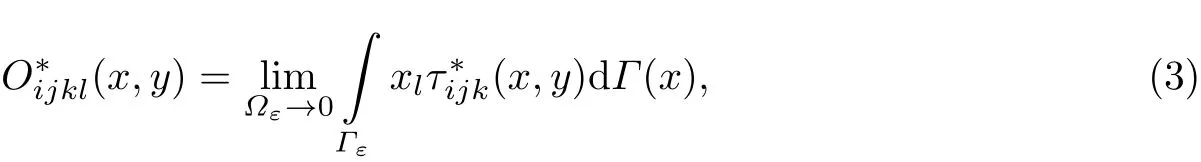
为式(2)域积分的自由项， Ωε为ΩI中ε无穷小域， 其边界为Γε， xl为场点 x 和源点 y 之间距离的粒子后， 区域ΩI中的本征应变.

在上述边界积分方程中， 本征应变及流体粒子的状态都是未知的， 需要在数值求解过程中逐步加以确定. 每个粒子的本征应变取决于外加应力(或者应变)、粒子的几何形状、粒子和基体的材料参数等因素. 需要指出的是， 边界积分方程(1)和(2)描述的是弹性均匀介质的应力场和位移场， 要描述含有非均质流体粒子的固体， 必须借助Eshelby 张量进行夹杂物的等效替换.

1.2 Eshelby 张量和等效夹杂理论

依据Eshelby 理论， 考虑二维全空间中的单个粒子， 在粒子域ΩI上存在的本征应变ε0kl满足

式中: δjl为 Kronecker 符号; μ 和 ν 分别为基体的剪切模量和泊松比. 需要说明的是， 式(5)的适用条件是本征应变在域ΩI内均匀分布， 并利用以下积分恒等式[12-13]，

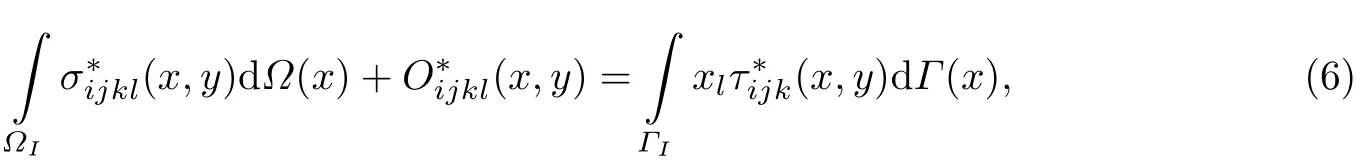
使得区域型积分转化为边界型积分. 假设流体为线性非黏性可压缩流体， 其本构关系可表示为

其中外加应变、拘束应变和本征应变三者应变偏量的表达式为

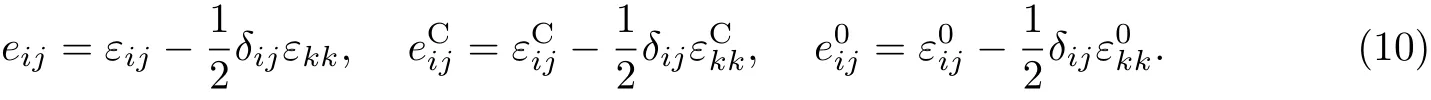
将式(8)和(9)改写为

式中:

将式(4)代入式(11)， 便得到流体粒子的本征应变与外加应变的关系，

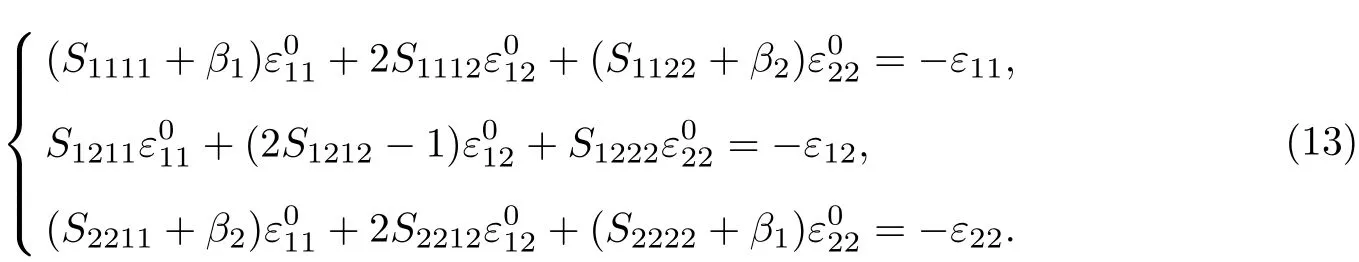
将式(13)改写成矩阵形式， 即

1.3 局部Eshelby 矩阵

当弹性固体中含有大量流体粒子时， 粒子间存在相互作用， 其大小取决于粒子间距离. 因此， 通过外加应力计算当前粒子的应变时， 除了要考虑远场荷载， 还需要考虑其他粒子对当前粒子的作用. 准确地说， 这种相互作用产生了两个因素需要考虑. 首先， 多粒子条件下本征应变不再是常数. 但是计算实践证明， 当粒子间无量纲距离满足一定条件时， 本征应变的常数假定能够近似成立[12-13]. 按本征应变的常数假定， 本模型中本征应变和外加应变都在粒子的几何中心处进行计算. 第二个需要考虑的因素是， 迭代计算的收敛性受到粒子间相互作用的影响. 为了考虑这一影响， 特别是处理近距离粒子间较强的相互作用， 将计算区域的粒子分成两组， 即近场群和远场群.

如图1 所示， 以当前粒子I 为中心， 将虚线所围成的圆内粒子定义为近场群粒子， 其他为远场群粒子. 假设全空间中近场群粒子数为N， 暂时忽略远场群粒子的作用， 利用式(2)， 当前粒子的应力边界积分方程可以表示成

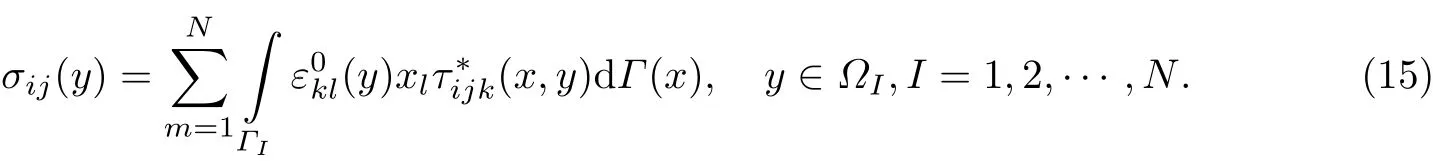
图1 全空间中当前粒子I 的近场群定义Fig.1 Definition of the near-field group for the current pore I in full space

运用Eshelby 张量和等效夹杂理论以及式(11)， 仿照1.2 节对单个粒子的推导过程， 将近场群粒子进行离散， 得到本征应变边界积分方程的矩阵形式

式中: {ε0}={ε01，ε02，··· ，ε0N}T表示近场群粒子的本征应变向量; {ε}={ε1，ε2，··· ，εN}T表示近场群粒子的外加应变向量; 矩阵[S]的表达式为

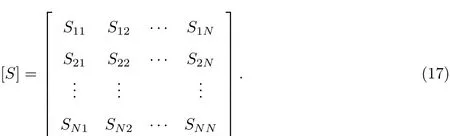
在矩阵[S]中， 主对角线元素Skk反映了粒子本身的本征应变和外加应变的关系， 非主对角线元素Sjk(j ／=k)表示近场群中k 粒子的外加应变对于j 粒子本征应变的影响. 矩阵[S]的结构与方程(14)中的矩阵S 相似， 其表达式参见式(13). 需要指出的是， 当粒子随机分布时， 每个粒子的近场群都是不同的. 假设当前粒子的编号为I， 每个粒子的本征应变向量ε0I都可通过其近场群粒子群的矩阵表达式和外加应变向量 {εI}={ε1， ε2，··· ，εN}TI计算得到，

式中: TI是对矩阵[S]求逆和缩并得到的， 称为局部Eshelby 矩阵. 这样， 基于本征应变边界积分方程和局部Eshelby 矩阵的算法， 固体中每个流体粒子的本征应变由以下三部分组成: 第一部分在外加载荷的作用下产生; 第二部分由近场群粒子之间的相互作用而产生， 通过式(18)计算得到; 第三部分由远场群粒子的弱相互作用产生， 通过迭代来计算[12-13].

2 数值算例

在数值算例中， 所有数值计算结果都通过本征应变边界积分方程法和子域边界积分方程法[14]获得. 利用边界点法对边界积分方程进行离散时， 对于奇异边界单元采用二次移动单元来离散， 对于非奇异边界单元采用常数单元来离散[15]. 对于粒子的边界或界面， 本征应变边界积分方程法和子域边界积分方程法分别用20 和40 节点来离散. 在所有的算例中， 泊松比取0.3， 杨氏模量取1. 圆形流体粒子的半径用r0表示， 椭圆形粒子的短轴与长轴之比定义为纵横比.

2.1 全空间中的单个圆形流体粒子

对于远场均布单位压力(p0=1)下全空间中的单个圆形流体粒子， 流体粒子的内部压力p、固体基体径向位移ur和径向应力σr的理论解[14]为

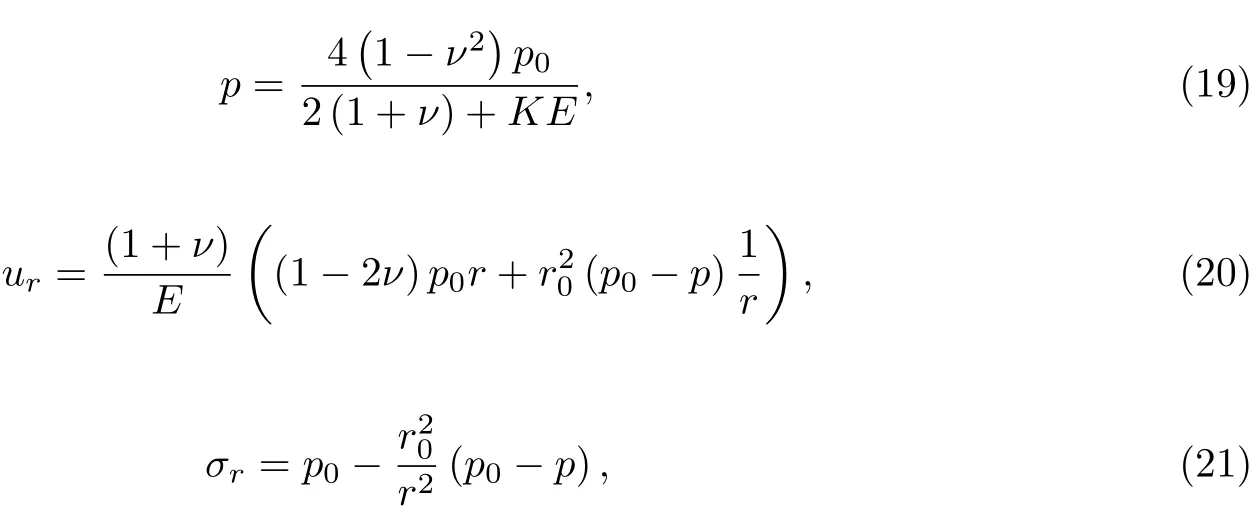
式(19)～(21)中: E 表示固体基体的弹性模量; K 表示流体粒子的压缩系数; r0为流体粒子半径; r 为全空间中粒子外部一点到流体粒子中心的距离.

表1 列出了分别采用本征应变边界积分方程法和子域边界积分方程法对单个圆形流体粒子的数值计算结果以及与理论解的对比， 表中负值表示压缩. 在表2 和3 中分别比较了3 种方法计算得到的基体内一点(x1=2r0， x2=r0)的径向位移和径向应力. 从表1～3 可以看出， 两个数值程序的结果与理论解的对比均具有很好的一致性， 虽然本征应变边界积分方程法使用了较少的节点， 但其计算结果比子域边界积分方程法更接近理论解， 显示了计算模型的正确性和可行性. 从理论上来说， 由于在本征应变边界积分方程法中， 边界未知量不直接出现在系统矩阵中， 因此较少的节点数不会明显降低其计算精度.

表1 单个圆形流体粒子内部压力的对比Table 1 Comparison of inner pressures in a single circular fluid-filled pore

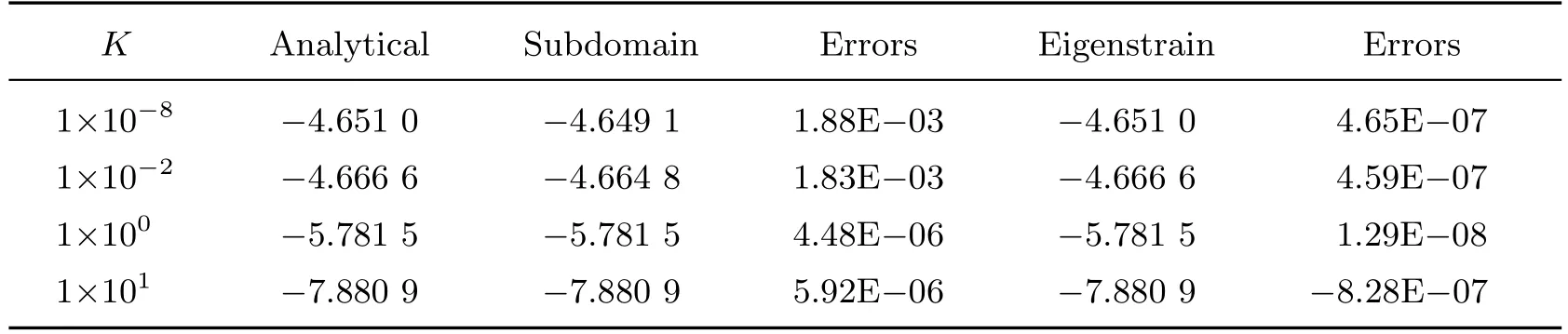
表2 固体基体中一点(x1 =2r0， x2 =r0)的径向位移对比Table 2 Comparison of radial displacements at the point (x1 =2r0， x2 =r0) in solid media

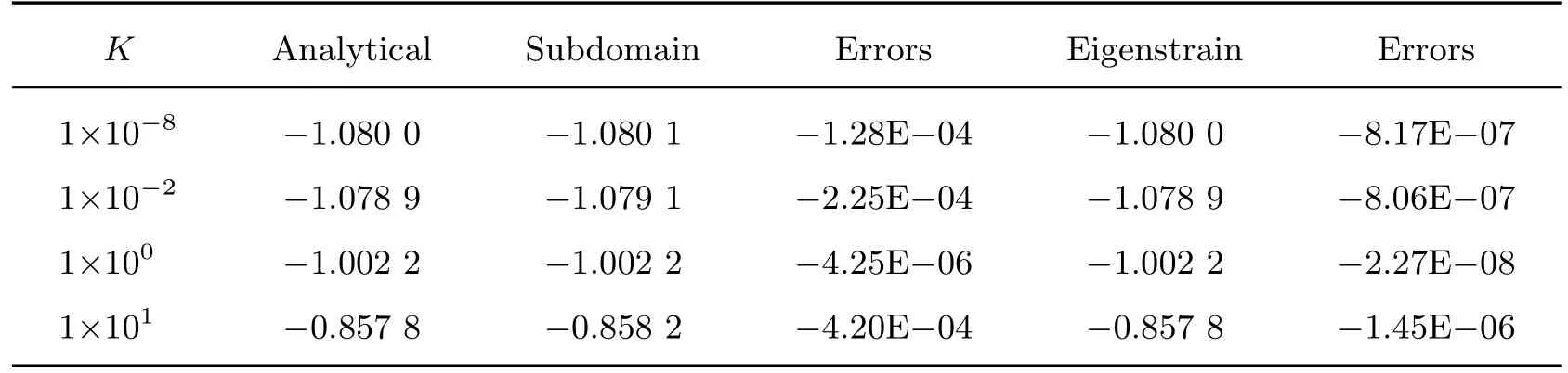
表3 固体基体中一点(x1 =2r0， x2 =r0)的径向应力对比Table 3 Comparison of radial stresses at the point (x1 =2r0， x2 =r0) in solid media

2.2 粒子附近处基体的应力

图2(a)和(b)分别比较了全空间远场均布双轴单位压缩荷载情况下， 2 和4 个圆形流体粒子附近基体的应力. 从图2 中可以看出， 本征应变边界积分方程法和子域边界积分方程法的结果相互吻合， 验证了本工作提出的计算模型的正确性和可行性.

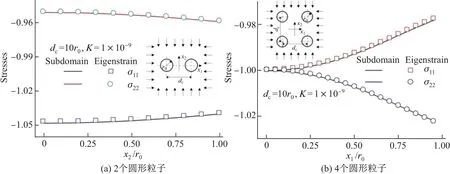
图2 全空间2 和4 个圆形粒子双向受压时粒子附近的应力Fig.2 Dimensionless stresses at solid media adjacent to the two and four fluid-filled pores under uniform biaxial compression in full space

2.3 含单个流体粒子的代表性体积单元的整体性能

在单轴压缩荷载条件下， 分别采用本征应变边界积分方程法和子域边界积分方程法对含有单个流体粒子(NI= 1)的正方形代表性体积单元(representative volume element， RVE)的整体性能进行计算和比较. 在两种数值方法中， 代表性体积单元的边界都用200 个节点进行离散.

图3(a)和(b)分别给出了含有单个圆形流体粒子的代表性体积单元的无量纲弹性模量E*/E 及泊松比ν*随孔隙率的变化. 孔隙率定义为流体粒子与代表性体积单元的面积之比.图4(a)和(b)分别给出了含有单个椭圆流体粒子的代表性体积单元的无量纲弹性模量E*/E 及泊松比ν*随孔隙率的变化， 其中E1*和ν1*分别表示加载方向和椭圆长轴都平行于x1方向时的整体性能， E2*和ν2*分别表示加载方向和椭圆短轴都平行于x2方向时的整体性能. 显然， 含有椭圆粒子时， 代表性体积单元的整体性能表现出各向异性. 图4 和5 表明两种计算方法得到的结果吻合良好.

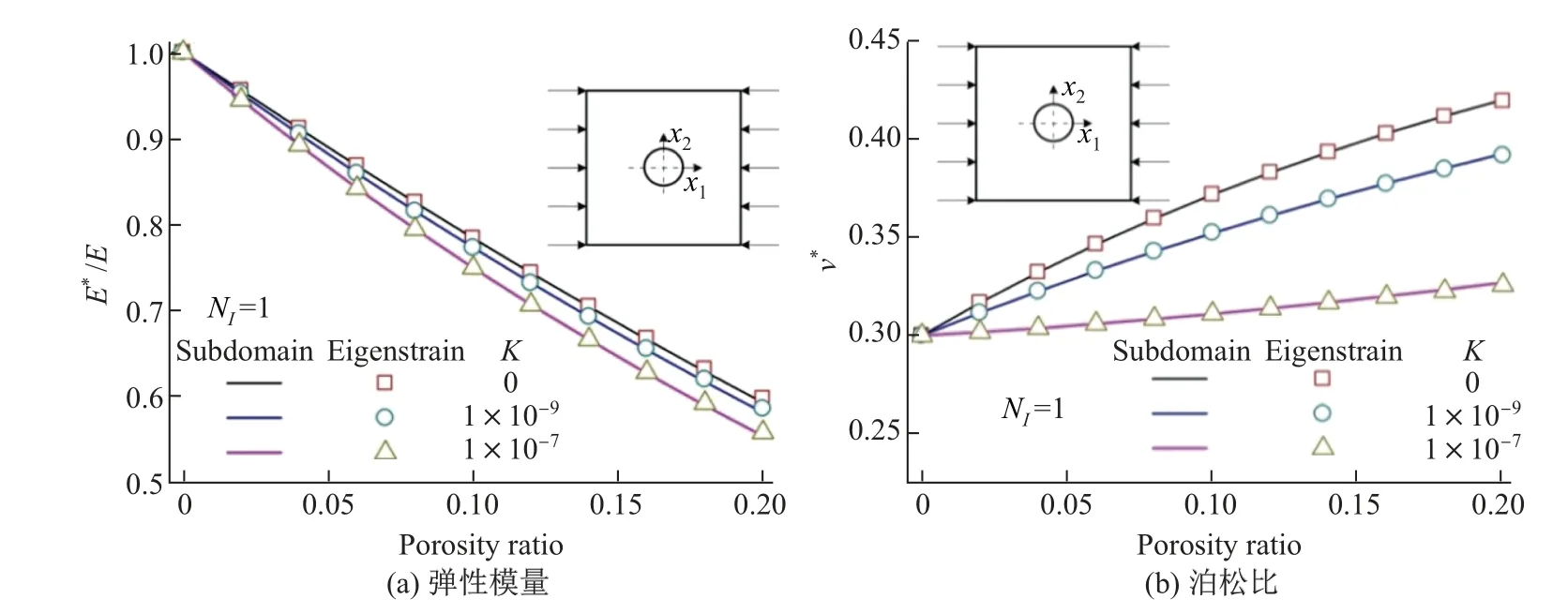
图3 RVE 中含单个圆形粒子时弹性模量和泊松比与孔隙率的关系Fig.3 Overall elastic modulus and Poisson’s ratio of RVE with a single circular pore as a function of porosity ratio

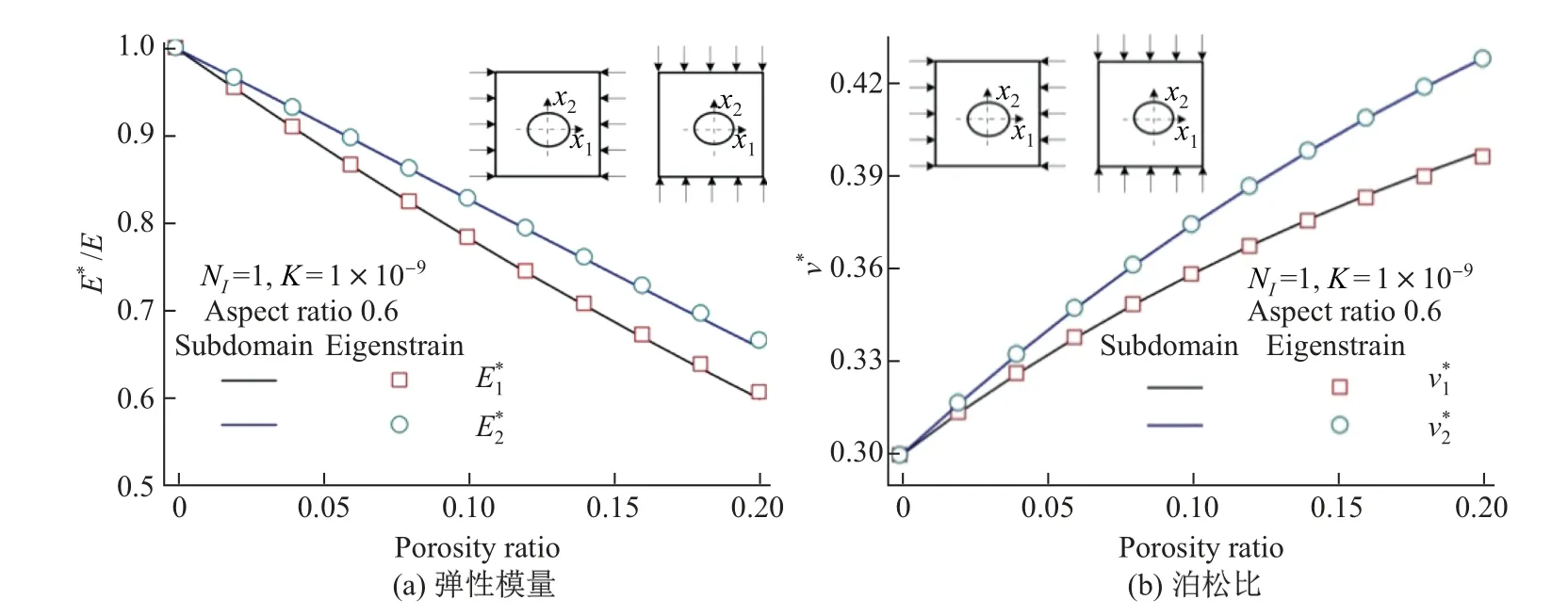
图4 RVE 中含单个椭圆粒子时弹性模量和泊松比与孔隙率的关系Fig.4 Overall elastic modulus and Poisson’s ratio of RVE with an elliptical pore as a function of porosity ratio

2.4 含多个流体粒子的代表性体积单元的整体性能

本工作计算分析了代表性体积单元中含有多个规则分布的流体粒子时的整体性能， 粒子的分布如图5(a)所示. 根据当前流体粒子位置的不同， 近场群的定义也有所不同(见图5(b)).图5(b)中编号1 的情况最常见， 其近场群包含9 个粒子. 而编号2 和3 的粒子分别靠近边界或角点， 近场群包含粒子数相对较少. 多粒子条件下代表性体积单元边界的离散、孔隙率的定义与2.3 节相同.

在保持孔隙率不变的条件下， 粒子数目对代表性体积单元整体性能的影响如图6 所示. 计算结果表明， 当流体粒子的数目增加到足够大， 即大约400 时， 若继续增加粒子的数目， 计算得到的代表性体积单元的弹性模量E*/E 和泊松比ν*均保持了相对稳定. 根据这一结果， 当讨论多粒子代表性体积单元的整体性能时， 选取的粒子数NI=1 089.

在单轴压缩条件下， 含多个圆形流体粒子的代表性体积单元的弹性模量和泊松比随孔隙率的变化如图7 所示. 在图7(b)中， 泊松比随孔隙率的变化表现出不同的趋势， 这一现象与流体的性质有关. 静态流体内部不存在切应力和切应变， 不存在对于形状改变的抵抗力， 而体积改变则与压缩系数有关. 随着压缩系数的减小， 流体粒子的力学性能将逐渐接近空洞的力学性能， 所以泊松比随孔隙率的增加而增大. 当压缩系数较大时， 随着孔隙率的增加， 粒子间的相互作用也随之增大， 使得泊松比反而减小. 这一整体性能的变化趋势与Kachanov 等[2]和Huang等[14]的计算结果也是一致的.

图5 RVE 中含有多个规则分布的圆形流体粒子示意图及3 种不同情况下近场群的定义Fig.5 Schematics of the RVE with multiple circular fluid-filled pores in regular distribution and the definitions of the near-field group in three different cases

图6 RVE 中含有多个圆形流体粒子时整体弹性模量和泊松比随粒子数NI 的变化Fig.6 Overall elastic modulus and Poisson’s ratio of RVE with multiple circular pores as a function of pore number NI

2.5 粒子随机分布对RVE 整体性能的影响

在实际问题中， 更常见的是固体中流体粒子的参数如位置、形状、大小和压缩系数等随机分布的情况， 这些参数可通过Fortran 语言中的伪随机函数random 来生成， 图8(a)中示意地给出了多粒子代表性体积单元中粒子位置随机分布的一种情况. 对于椭圆粒子， 其倾角θ 如图8(b)所示. 本工作计算了两种不同随机粒子分布时的代表性体积单元的体积模量， 并与流体粒子规则分布的代表性体积单元的体积模量进行了比较. 第一种为压缩系数在10-9～100范围内随机变化且流体粒子的位置随机变化; 在此基础上， 第二种随机分布增加了粒子大小以及椭圆粒子倾角的随机变化， 计算中椭圆粒子的纵横比保持不变(0.6).

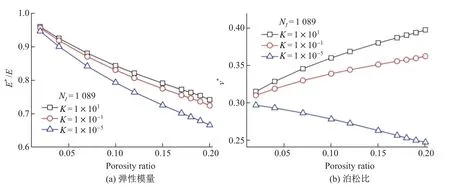
图7 双向受压时含多个圆形流体粒子的RVE 的弹性模量和泊松比与孔隙率的关系Fig.7 Overall elastic modulus and Poisson’s ratio of RVE with multiple circular pores as a function of porosity ratio under uniaxial compression

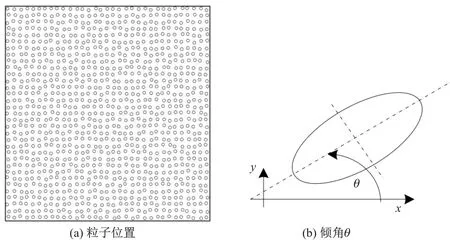
图8 RVE 中含有多个位置随机分布的流体粒子示意图及椭圆粒子倾角θ的定义Fig.8 Schematics of the RVE with multiple fluid-filled pores in random distribution by position and the definition of tilting angle θ of elliptic pore

在双轴均匀受压荷载下， 本工作计算了两种不同随机粒子分布时的代表性体积单元的体积模量随孔隙率的变化， 并与粒子规则分布时的结果进行了比较， 如图9 所示. 结果表明， 两种随机分布时的体积模量分别与压缩系数K =8.75×10-2和4.55×10-2的规则分布时的代表性体积单元的体积模量相吻合. 由此可知， 在一定条件下， 随机分布流体粒子固体的整体性能可以借助于具有规则分布粒子的固体来进行研究. 然而这一做法的效果是有限的， 因为粒子参数与固体力学性能的关系比较复杂， 需要借助数值计算的手段进行研究， 特别是粒子随机分布的情况. 本工作提出的计算模型为这一研究提供了有效的工具.

2.6 计算效率

图10 给出了本征应变边界积分方程法和子域边界积分方程法CPU 时间的对比. 可以看出， 随着粒子数的增加， 本征应变边界积分方程法计算模型的效率远高于子域边界积分方程法， 因为在子域边界积分方程法中， 系统矩阵的维数随着粒子数的增加而呈几何级数增长， 当粒子数超过百位数时， 由于计算机内存的限制， 程序已无法运行. 而在本征应变边界积分方程法计算模型中， 系统矩阵的维数与粒子数无关， 只有局部Eshelby 矩阵的数量与粒子数成正比，计算量随着粒子数的增加按算术级数增加， 因此本工作提出的计算模型具有极高的计算效率.

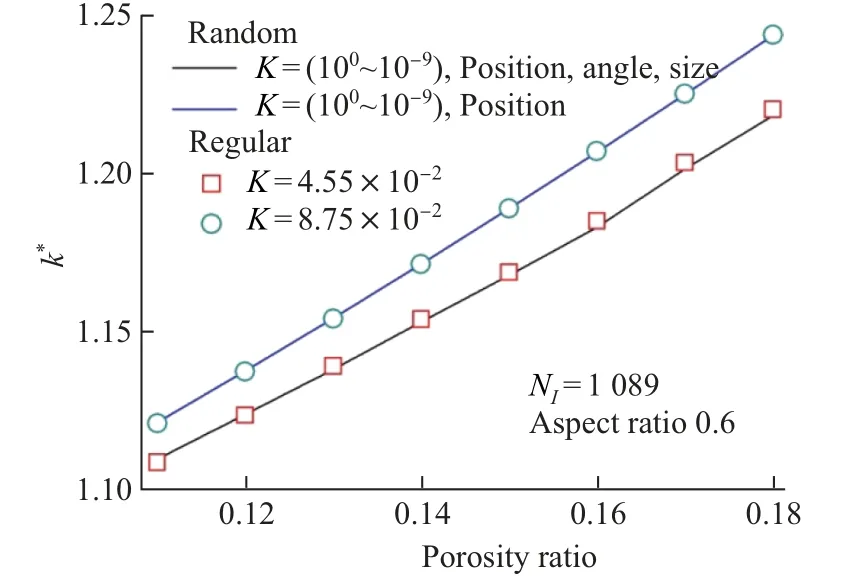
图9 RVE 中含有多个流体粒子时随机分布和规则分布的体积模量随孔隙率变化的对比Fig.9 Comparison of overall bulk modulus of RVE with multiple pores between random and regular distributions as a function of porosity ratio

图10 两种计算模型(本征应变法和子域法)CPU 时间随粒子数NI 变化的对比Fig.10 Comparison of CPU times for the two computing procedures，the Eigenstrain and the Subdomain， as a function of total pore numbers NI

3 结束语

本工作将Eshelby 本征应变和等效夹杂理论引入边界积分方程中， 提出了含大量流体粒子固体的本征应变边界积分方程的计算模型及迭代算法. 通过全空间中近场群的定义和局部Eshelby 矩阵的引入， 解决了粒子间相互作用的问题， 保证了迭代计算的收敛性. 通过数值算例的比较， 不仅验证了所提出计算模型的正确性和计算方法的可行性， 也证明计算模型具有很高的计算效率， 为含有大量流体粒子固体的数值模拟提供了新的有效的研究手段.