基于机器学习方法的二维材料带隙预测

游 洋， 杜 婉， 李惟驹， 陈竞哲

(1. 上海大学理学院， 上海200444;2. 上海大学量子与分子结构国际研究中心， 上海200444;3. 上海大学材料基因组工程研究院， 上海200444)

二维材料， 又称单层材料， 是由单层或少数几层原子组成的， 是在垂直方向上不具备平移周期性的晶体材料. 二维材料具有诸多令人瞩目的物理、化学性质， 使其成为目前材料科学研究的前沿焦点. 二维材料通常可以归类为各种元素或化合物的二维同素异形体， 其电子能带结构和三维的母体材料往往有很大不同. 由于二维材料只具有单层或少数几层原子， 尺寸受限会带来量子限域效应， 而且原子都暴露在表面， 更容易被调控. 二维材料主要有石墨烯、磷烯、硼墨烯、过渡金属硫化物[1]、过渡金属卤化物[2]等， 其中以MoS2， MnCl2为代表的过渡金属硫化物(transition metal chalcogenides， TMCs)和过渡金属卤化物(transition metal halides，TMHs)成为研究热点. TMCs 和TMHs 的化学通式为MX2， 其中M为第四到第十族过渡金属元素， X 为硫族或卤族元素. 相较于石墨烯， TMCs， TMHs 因为具有更多的组分和结构， 从而具有许多独特的物理和化学特性.

带隙是表征半导体和绝缘体用于光学和电子应用的简单而重要的参数[3]. 由于准确测量带隙需要高质量的单晶， 所以从实验获得的带隙数据非常少. 随着计算机技术的进步， 第一性原理方法(first-principles method)成为计算大量化合物带隙的常用方法[4]. 大部分材料的电子结构都是基于密度泛函理论(density functional theory， DFT)计算， 将得到的Kohn-Sham 带隙[5]， 即最低未占据和最高占据能量特征值之间的差异作为近似带隙. 但由于理论局限， 基于DFT 计算出的带隙往往都小于真实值. 为了获得更准确的带隙， 经常采用一些更复杂的方法，例如基于多体扰动理论的GW 方法[6]. 但高精度的G0W0计算耗时长， 占用资源多， 计算的体系原子数较少. 因此， 希望寻找一种在计算成本上可承受且能较为准确估计带隙的替代方法.

随着人工智能的发展， 很多研究者提出将机器学习方法应用在基础学科上. 在目前所产生的大量材料数据集上使用不同的机器学习方法进行新材料的性能预测， 可以有效提高材料性能预测准确率， 节约计算成本， 也可为材料实验和应用提供指导.

本工作以COMPUTATIONAL MATERIALS REPOSITORY 数据库[7]中基于第一性原理和密度泛函理论计算的化学通式为MX2的二维材料数据集为蓝本， 提取化合物的总能量(energy)、形成热(heat of formation)、带隙(bandgap)， 分别基于广义梯度近似(general gradient approximation， GGA)-Perdew-Burke-Ernzerhof (PBE) (GGA-PBE)和 G0W0计算作为特征变量， 并加入M， X 原子电负性(electronegativity)、第一电离能(first ionization energy)和原子的有效原子半径(radius)等性质， 来预测更为精确的带隙. 如图1 所示， 将原始数据集随机分为训练集(training set)和测试集(testing set)， 然后分别选用套索回归， 即最小绝对值收敛和选择算子(least absolute shrinkage and selection operator， LASSO)[8-9]、支持向量回归(support vector regression， SVR)[10-12]、梯度树提升回归(gradient boosting regression，GBR)[13-14]三种机器学习方法对数据进行训练， 同时采用交叉验证的方法建立带隙的预测模型. 最后， 利用所得模型对测试集进行预测， 并对预测结果进行评估. 这种方法避免了第一性原理计算， 从而能够提高研究效率并降低研究成本.

图1 机器学习预测模型的基本流程Fig.1 Basic flow of machine learning prediction model

1 机器学习原理和方法

机器学习是一类从数据中自动分析获得规律， 并利用规律对未知数据进行预测的算法[15-16]， 即从给定的含有输入(特征)和输出(目标)的训练数据中学习得出一个模型， 当添加新的数据时， 可以根据这个模型来预测结果. 对于连续性目标变量的分析预测， 一般采用回归模型(regression model)方法[17].

1.1 LASSO 算法

LASSO 算法是一种同时进行特征选择和正则化的回归分析方法， 旨在增强统计模型的准确性和解释性， 常用于广义线性回归模型.

线性回归模型描述特征(特征变量xi)与连续输出(目标变量y)的关系为

式中: w0为权值; wi为特征变量的系数. 要拟合带有系数wi的线性模型， 最简单的方法是使用普通最小二乘法(ordinary least squares， OLS). 然而， 普通最小二乘的系数估计依赖于模型各项的相互独立性， 当各项相关时， 会导致最小二乘估计对于随机误差非常敏感， 从而产生很大的方差. 而LASSO 通过强制使回归系数绝对值之和小于某固定值， 有效地构建了不包括这些回归系数对应协变量的更精准的模型， 从而改善模型的预测偏差. 在数学表达上， LASSO 由一个带有L1 先验的正则项[8]的线性模型组成， 其最小化目标函数为

LASSO 回归复杂度由参数λ 来控制， λ 越大， 对变量较多的线性模型的惩罚力度就越大， 从而最终获得一个变量较少的模型.

1.2 SVR 算法

SVR 是基于支持向量机(support vector machine， SVM)发展而来的. SVR 的基本思想是通过一个非线性映射Φ， 将数据x 映射到高维特征空间， 并在这个空间进行线性回归. 假设一个样本集 {(xi，yi)}Ni， 其中输入数据xi∈ Rn， yi∈ R， 在高维空间中构造的最优线性模型函数为

式中: ω 为权重; b 为偏置项. 这样， 在高维特征空间的线性回归便对应于低维输入空间的非线性回归.

利用SVR 解决回归问题时， 需要根据问题选择适当的核函数来代替内积， 以便隐式地把高维特征空间的点积运算转化为低维原始空间的核函数运算[18]. 核函数不仅要在理论上满足Mercer 条件[19]， 而且在实际应用中要能够反映训练样本数据的分布特性. 常用的核函数有线性(linear)核、径向基(radial basis function， RBF)核等.

SVM 泛化为SVR 是通过在高维空间最小化ε 不敏感损失函数来解决回归问题[12]， 同时通过最小化‖ω‖2来降低模型的复杂度. 常用的损失函数有线性ε 不敏感损失函数、二次ε 不敏感损失函数等.

SVR的目标函数为

式中: ξ 和ξ*是非负的松驰变量; 正则项C 是控制对超出误差的样本的惩罚程度. 使用支持向量回归构建模型， 首先要明确模型的输入与输出， 然后选择合适的核函数、损失函数以及调整参数如核参数σ、正则项C、不敏感损失参数ε， 最终根据样本训练集得到训练模型.

1.3 GBR 算法

GBR 属于Boosting 算法的一种改进. Boosting 是一类将弱学习器提升为强学习器的集成学习算法. Boosting 算法初始为每一个样本赋上一个相等的权重值， 由于每一次训练都会使数据点的估计有所差异， 所以在每一步结束后， 通过增加错分点对权重值进行处理， 然后进行N 次迭代， 得到 N 个简单的基分类器(basic learner)， 最后将 N 个基分类器加权组合起来， 得到一个最终模型.

GBR 与Boosting 的区别在于， GBR 的每一次计算都是为了减少上一次的残差(residual)，而为了减少这些残差， 需要在残差减少的梯度方向上建立一个新模型. 所以在GBR 中， 每个新模型的建立是为了使得先前模型残差往梯度方向减少， 再利用当前模型中损失函数的负梯度值作为GBR 算法中残差的近似值， 进而拟合出回归树[13].

梯度树提升回归算法一般使用固定大小的回归树作为弱分类器， 回归树本身拥有的一些特性使其能够在提升过程中变得更准确， 即处理混合类型数据以及构建具有复杂功能模型的能力. GBR 模型为

式中: rm表示权重; T(x;Θm)表示回归树， Θm为回归树的参数; m 为树的个数.

1.4 性能评估

本工作利用平均绝对误差（mean absolute error， MAE）、均方误差（mean squared error，MSE）和R2值作为机器学习预测结果的评估标准.

式(6)～(8)中: n 为样本数量; ^yl为真实值; yi为预测值.

2 数据处理与模型建立

使用机器学习方法进行带隙预测的过程中， 研究对象及其数据的选取尤为重要. 为了建立可靠的二维材料数据集， 本工作选取了主族金属元素、过渡金属元素、氧族与卤族元素组成的结构类似的MX2型二维材料为研究对象， 根据不同的相态分为1-T 和2-H 类型[20]， 这样共得到约几百种化合物， 挑选其中具有一定带隙的化合物进行研究.

从数据库COMPUTATIONAL MATERIALS REPOSITORY 中选取基于第一性原理和密度泛函理论计算得到的136 个MX2型二维金属化合物数据作为原始数据集. 提取M， X 位元素的电负性(EN)、第一电离能(I)和原子的有效半径(R)， 以及化合物的形成热(Hf)、总能量(E)、晶体体积(V)、晶体质量(m)， 基于GGA-PBE 计算的低精度带隙(PBE)等性质为特征参数， 以G0W0的带隙为预测目标， 组成标准数据集， 进行机器学习.

根据获得的数据集和预测变量， 基于机器学习的二维材料带隙预测模型构建方法如下.

(1) 数据准备: 将136 组数据的数据集随机分成120 组数据组成的训练集和16 条数据构成的测试集.

(2) 模型训练: 设置 10 折交叉验证[21]， 分别建立 GBR， SVR， LASSO 算法模型， 利用 3 种模型对训练集的G0W0带隙进行训练.

(3) 模型效果评估: 使用MAE， MSE， R2等评价指标对模型效果进行评估.

(4) 模型应用: 利用训练后的多个算法模型对测试集的带隙进行独立预测， 并简单评估.

为了提高模型预测精度， 在模型训练之前通常要对算法进行参数寻优. 例如， 采用GBR算法时， 通过迭代选择可以得到最佳的弱学习器个数大致在190～200 之间; 对于SVR 算法， 通过迭代选择最佳的惩罚项参数为0.5. 由于样本集数量不大， 因此将模型算法的其他参数设置为默认值.

3 实验结果与分析

本工作结合136 个样本材料的特征参数， 通过热图(heatmap)表示数据集中材料性质特征之间的关系(见图2(a)). 另外， G0W0带隙与PBE 带隙的关系如图2(b)所示.

从图2(a)中可以看出， G0W0带隙与PBE 带隙的相关性最强， 而且X 位元素的电负性和电离能与带隙也具有一定的相关性. 从图2(b)中更能看出， PBE 带隙与G0W0带隙之间具有很强的线性关系， 且G0W0带隙总要高于PBE 带隙. 因此， 可以将PBE 带隙值作为计算代价较高的G0W0带隙的预测模型的重要特征.

图2 样本各特征之间的相关性以及PBE 带隙与G0W0 带隙之间的关系Fig.2 Correlation between features and relationship between PBE bandgap and G0W0 bandgap

利用SVR， LASSO， GBR 三种机器学习方法对训练集进行学习训练， 可以得到如图3 所示的模型， 图中横坐标为G0W0的理论计算值， 蓝点的纵坐标为对应的G0W0带隙预测值， 黄点为对应的PBE 带隙. 可以看出， G0W0带隙预测值明显比PBE 带隙更准确， 即比PBE 的带隙值更接近G0W0带隙. 进行10 折交叉验证后， 得到3 种算法在交叉验证过程中的准确度如表1 所示.

图 3 SVR， LASSO， GBR 回归模型Fig.3 SVR， LASSO， and GBR regression models

表1 不同模型的10 折交叉验证准确度Table 1 10-fold cross-validation results for different models

从表1 中可知， 3 种算法训练出的模型效果都比较理想， 其中SVR 算法选用的核函数为线性核函数， 而LASSO 本身就是带有惩罚项的线性回归. 所以可以断定， 采用线性回归的机器学习方法更符合数据集的特点， 从表2 所示的误差分析中也可以得到相同的结论. 当选取核函数时， 如果用最常用的径向基核函数， 那么得到的结果反而非常差， 这是因为SVR 算法对于核函数的高维(11 维)映射解释力不强， 尤其是RBF 核函数的SVR 算法.

表2 训练集拟合结果比较Table 2 Comparison of training set fitting results

图 4 SVR， LASSO， GBR 回归模型对测试集的预测结果Fig.4 Prediction of the testing set by SVR， LASSO， and GBR regression models

用训练好的模型对测试集的16 个样本进行预测， 图4 直观地反映出预测结果并与PBE带隙相比较. 从图中可以看出， LASSO 和SVR(基于线性核)对测试集的预测与模型预测趋势符合较好. 而GBR 预测的结果误差要比模型误差大， 说明GBR 这种集成学习算法数据的敏感度更高， 虽然可以得到拟合很好的模型， 但对于未知模型， 过拟合的风险会更大. 表3 显示了测试集测试结果的比较.

表3 不同测试集算法预测结果比较Table 3 Comparison of the prediction by different models in testing set

从表4 数据可以看出， 3 种模型在二维材料带隙极小(≤0.8 eV)的情况下进行预测， 得到的预测带隙误差较大; 但在合理的范围(1 eV≤G0W0≤8 eV)内， 预测值与真实值非常接近，平均误差为0.5 eV. 在选取模型时， 基于线性核函数的SVR 模型和带有惩罚项线性回归的LASSO 模型预测得到的带隙值非常相似， 而且由于采用了线性回归的方法， 算法的复杂度并不高， 更能提高今后大数据量研究的计算效率. 而由图3 可以看出， GBR 模型的线性相关度更高， 但是结合测试集预测结果的对比与误差分析， 虽然在少数情况下GBR 的预测精度在SVR与LASSO 之间， 但在大多数情况下SVR 和LASSO 的预测精度更好， 而造成这种结果的原因是GBR 对未知数据过拟合的概率更大.

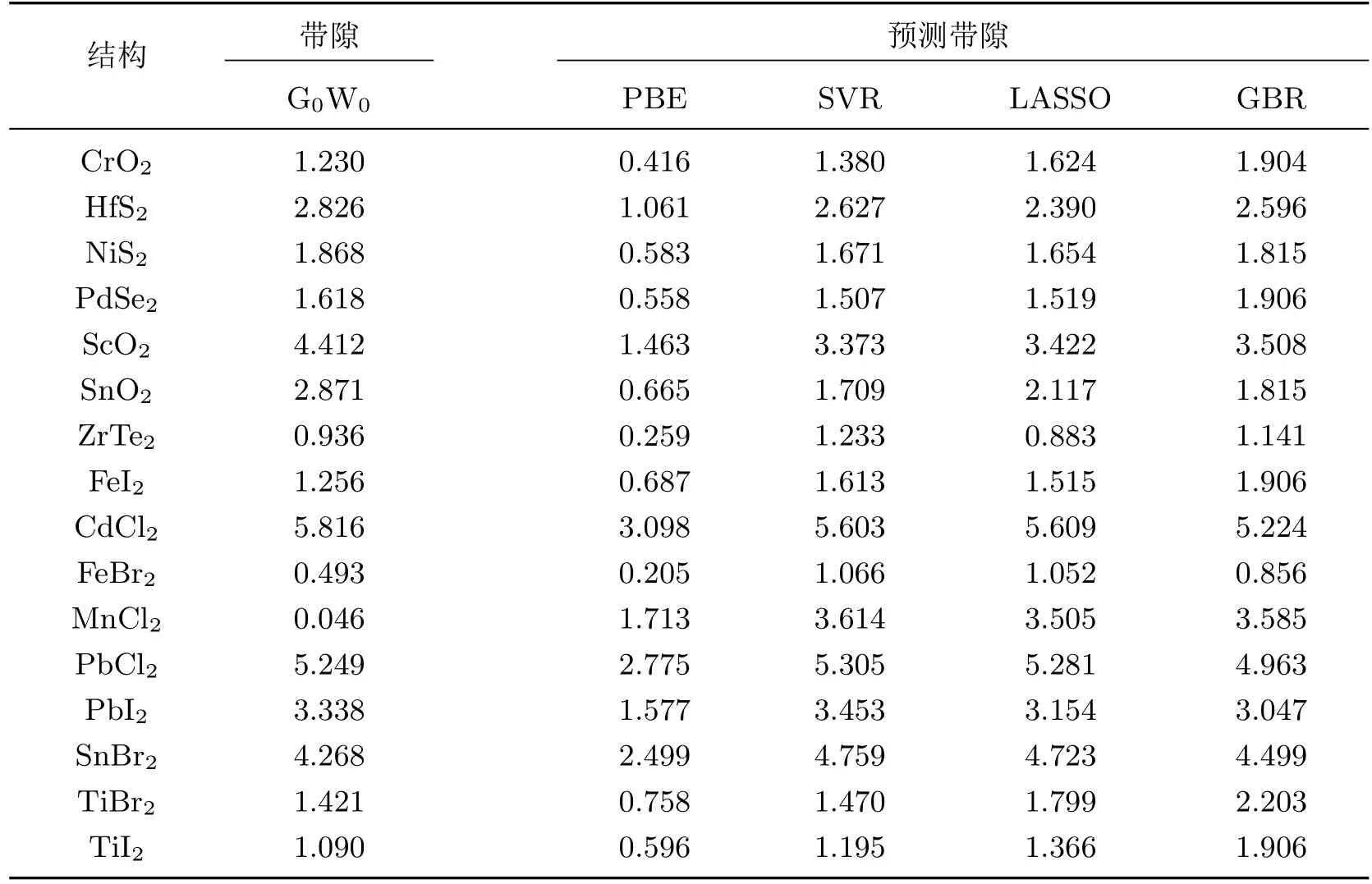
表4 测试集预测带隙的比较Table 4 Comparison of bandgap’s prediction in testing set

4 结束语

本工作利用机器学习方法结合密度泛函理论， 探索了预测二维半导体材料基本带隙的方法. 所选取的二维材料具有相似的晶体结构， 带隙值约为0～8 eV. 基于机器学习方法， 训练了可以预测带隙值的模型. 本工作讨论的模型中， 当PBE 结果和元素信息被用作预测因子时，运用SVR 算法建立的模型具有最佳性能， 训练集与测试集的MAE 分别为0.335 和0.540 eV.而具有惩罚项的线性回归算法LASSO 在二维材料带隙的预测中也表现出极好的效果. 因此，基于机器学习方法对二维材料的带隙预测是可行的.

另外， 本工作所提出的预测模型可用于更复杂系统(如多元化合物和合金)的电子性质预测， 为今后对新型材料的探索和研究提供了一种新的方法.