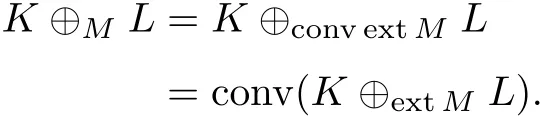极体算子与M-加算子的极表示

刘 畅， 冷岗松

(上海大学理学院， 上海200444)

经典的Brunn-Minkowski 理论的研究对象是凸体， 极体是一个十分重要的概念， 与极体相关的著名的Mahlar 猜想仍是一个公开问题. 事实上， 对于原点对称的凸体， 都有一个赋范线性空间(Rn，||·||)与其一一对应. 而与该凸体的极体一一对应的， 是赋范线性空间(Rn，||·||)的对偶空间. 对Rn中的集合， Schneider[1]定义极体如下.

定义1 K 是Rn的非空子集， K 的极体定义为

Brunn-Minkowski 理论是凸几何中的核心理论， 与Minkowski 问题相关的研究参见文献[1-3]. Minkowski 加法在经典的Brunn-Minkowski 理论中具有重要作用， 也在计算机和机器人领域有一定的应用. 对于两个给定的凸体K，L， Minkowski 加法定义如下:

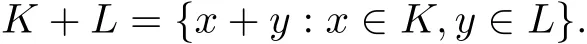
Minkowski 加法的一个重要推广是 M-加. M-加是Protasov[4]首先引入的， 对中心对称的紧凸集K 和L 以及R2中的无条件凸体M， 在范数代数中研究联合谱半径时用到K ⊕ML. Green等[5]和Motakin[6]都对M-加进行了广泛的研究， 而´Curgus等[7]应用Green等[5]和Motakin[6]的结果实现了Gauss-Lulas 定理在多项式根上的改进. 当m =2，n ≥ 2 时， Gardner等[8]定义 ⊕M如下.

定义 2 K，L 是 Rn的子集， M 是 R2的子集， K，L 的 M-加定义为

通过比较M-加和Minkowski 加法得到M-加的等价定义为

由文献[1]中的定理， 即每个凸体K 是它的极值点的凸包， 即K = conv ext K ， 可知一个凸体可以用比它更小集合的凸包表示. 基于此思想， 本工作 探究集合K 的极体能否用比 K 更小集合的极体表示， M-加算子能否用 M′-加表示， 其中 M′⊂ M. 尽量找到 M′， 使 M′最小.

本工作主要得到以下结论.

定理1 对Rn中的有界闭子集K， K°=(bd K)°.

定理 2 对Rn中的凸体K， K°=(ext K)°.

定理 3 当 M ⊂ Λ1且 M ∈ K2， K，L ∈ Kon时， K ⊕ML=K ⊕bdML.

定理 4 当 M ⊂ Λ1且 M ∈ K2， K，L ∈ Kn时， K ⊕ML=conv(K ⊕extML).

1 预备知识

本工作用 Rn表示 n 维欧式空间， 赋予了标准内积 〈·，·〉. B，Sn-1为 Rn上的单位球和单位球面. 将Rn中具有非空内点的紧凸集称为凸体. Kn表示Rn中的所有凸体的集合， Kno表示所有包含原点的凸体的集合(下述记号和定义参考文献[1，9]).

对于Rn中的子集A， 记bdA， cl A， int A 分别为A 的边界、闭包、内部. A 的凸包定义为

若 z 不可以表示成 z =(1- λ)x+ λy， 其中 x，y ∈ A，x ／=y，λ ∈ (0，1)， 则 z 是 A 的极值点.所有A 的极值点构成的集合记为extA.

对 A 的一个凸子集 F， 若对任一线段 [x，y]⊂ A 满足 F ∩ relint[x，y]／= ∅ 仍包含在 F 中，则称F 是A 的一个面.

A 的极射线是一条射线， 且这条射线是A 的一个面. 所有A 的极射线的并集记为extrA.

令 Λn1={(λ1，λ2，··· ，λn)∈ Rn|λi≥ 0， i=1，2，··· ，n}， 表示 n 维欧氏空间第一象限点的集合. 若 n=2， 将 Λ21简记为 Λ1.

2 极体的极表示

这一节探究凸几何中的极体算子K°能否用比K 更小的集合的极体表示. 探究K 的极体是否等于bd K 的极体， 进一步考虑是否等于ext K 的极体， 并探究取等条件.

下面的定理1 说明了当K 是Rn中有界闭子集时， 有K°=(bd K)°. 例1 说明当K 无界时， 二者不一定相等.

定理 1 当K 是Rn中的有界闭子集时， K°=(bd K)°.

证明 首先证 K°⊂ (bd K)°.

由定义1 知

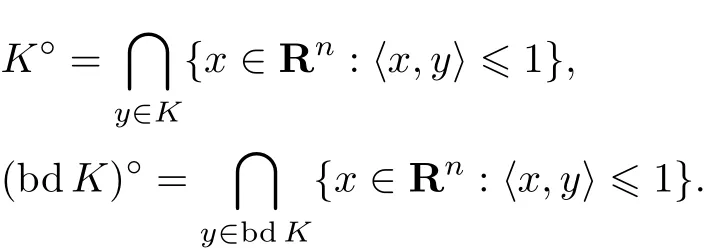
因为 bd K ⊂ K，故 K°⊂ (bd K)°.

再证 (bd K)°⊂ K°.

对 ∀x ∈ (bd K)°， 下面证明 ∀y ∈ int K 和 ∀y ∈ bd K 都有 〈x，y〉≤ 1.

当 y ∈ int K，∃ y1，y2∈ bd K， 使得

从而有

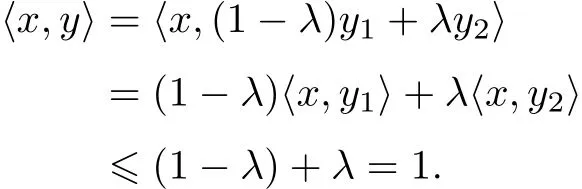
当 y ∈ bd K， 显然 〈x，y〉≤ 1.

故对 ∀y ∈ K， 有 〈x，y〉≤ 1， 由定义 1 知 (bd K)°⊂ K°.

因此 K°=(bd K)°.

例 1 在 R2中 K = {(x，y) : y ≥ 0}， 由极体的定义可知 (bd K)°= {(x，y) : x = 0}. 而K°={(x，y):x=0，y ≤ 0}. 故 K°／=(bd K)°.

由例1 知K 有界是K°=(bd K)°的一个必不可少的条件. 定理1 说明了当K 为有界闭集时 K°=(bd K)°. 下面的推论 1 探究 K°和 (int K)°是否相等. 为此， 先证明 K°=(cl K)°(引理1)和cl K =cl int K (引理2).

引理1 对Rn中的非空集合K， 有K°=(cl K)°.

证明 首先证 (cl K)°⊂ K°.

因为 K ⊂ cl K， 故由定义知 (cl K)°⊂ K°.

再证 K°⊂ (cl K)°.

对 ∀x ∈ K°， 由于 ∀z ∈ cl K，∃{zn} ⊂ K， 使得 zn→ z(n → ∞)， 故

故 x ∈ (cl K)°， 因为 x ∈ K°是任意的， 故 K°⊂ (cl K)°.

因此 K°=(cl K)°.

引理2[1]当K 是Rn中具有非空内点的凸集时， cl K =cl int K.

推论1 当K 是Rn中具有非空内点的凸集时， K°=(int K)°.

证明 由引理1 和引理2 可得到结果.

通过上面的证明可得， 对有界闭集K， K°等于(bd K)°; 当K 是具有非空内点的凸集时，K°等于 (int K)°. 由此猜想， K°可能与 (ext K)°有关系， 由定理 2 得到当 K 为 Rn中的凸体时， K°=(ext K)°; 定理 2 的证明用到了引理 3， 因此首先引入引理 3， 再来证明定理 2.

引理3[1]每个凸体K 是它的极值点的凸包， 即K =conv ext K.

定理 2 当 K ∈ Kn时， K°=(ext K)°.

证明 由极体的定义知K°⊂(ext K)°.

再证 (ext K)°⊂ K°.

对 ∀x ∈ (ext K)°， 由引理 3 知 K =conv ext K. 注意到对 ∀y ∈ K， 有

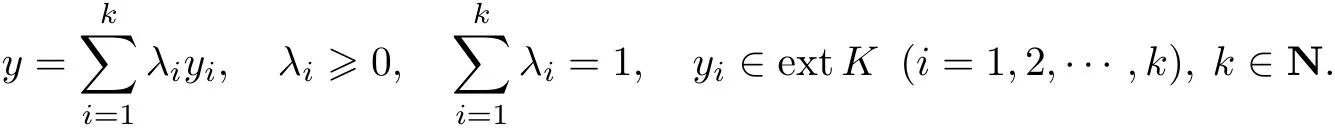
从而

故 x ∈ K°. 因为 x ∈ (ext K)°是任意的， 故得 (ext K)°⊂ K°.

因此 K°=(ext K)°.

下面探究K 不包含直线的闭凸集的情形. 为证明推论2， 需要先证明引理4 和引理5.

引理4 对Rn中的非空集合K， 有K°=(conv K)°.

证明 首先由定义知(conv K)°⊂K°显然成立.

再证 K°⊂ (conv K)°.

对 ∀x ∈ K°， 有 〈x，y〉≤ 1 对 ∀y ∈ K 成立.

因此 K°=(conv K)°.

引理5[1]当K 是Rn中不包含直线的闭凸集时， K =conv(ext K ∪extr K).

推论 2 当K 是Rn中不包含直线的闭凸集时， K°=(ext K ∪extr K)°.

证明 由引理5 可知，

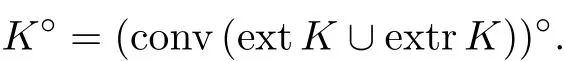
由引理4 可知，

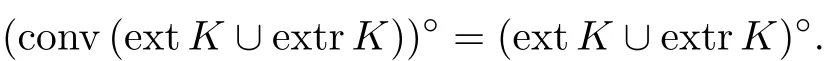
故

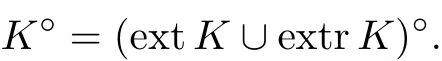
综上， 对 Rn中的有界闭子集 K， K°= (bd K)°; K 是 Rn中具有非空内点的凸集，K°= (int K)°， 对 Rn中的凸体 K， K°= (ext K)°; 对不包含直线的闭凸集 K， K°=(ext K ∪ extr K)°.

3 M-加的极表示

这一节研究M-加算子能否用M′-加表示， 其中M′⊂M. 考虑M 的边界点和极值点构成的集， 探究 K ⊕ML 和 K ⊕bdML 是否相等， 以及等号取得时对 M，K，L 的限制. 进一步考虑K ⊕extML 能否用来表示K ⊕ML.

首先讨论 K ⊕ML 和K ⊕bdML 是否相等， 定理 3 证明了当M 为凸体且位于R2的第一象限， K，L 为 Rn中包含原点的凸体时， 有 K ⊕ML=K ⊕bdML.

定理 3 当 M ⊂ Λ1且 M ∈ K2， K，L ∈ Kno时， K ⊕ML=K ⊕bdML.

证明 因为 bd M ⊂ M， 故 K ⊕bdML ⊂ K ⊕ML.

下证 K ⊕ML ⊂ K ⊕bdML.

对任意 α1x+ α2y ∈ K ⊕ML， 因为 0 ∈ K ∩ L， 故对 ∀λ ≤ 1， 有

且 M ⊂ Λ1， 必存在 λ ≤ 1， 使得

则

故 K ⊕ML=K ⊕bdML.

若将 M，K，L 的限制移除， K ⊕ML 和 K ⊕bdML 不一定相等. 反例参见例 2 和例 3.

例 2 令 M = [-1，1]× [-1，1]，K = {e1}，L = {e2}，P1，P2，P3，P4是集合 M 中的点， 坐标分别为 (-1，1)，(1，1)，(-1，-1)，(1，-1).因为 (0，0)∈ M， 故

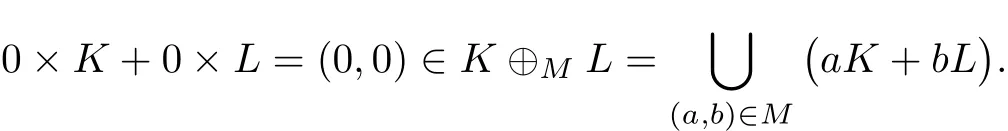
下证 (0，0)不在 K ⊕bdML 中.令 PiPj(1 ≤ i，j ≤ 4)表示连接 Pi，Pj的闭线段(见图1).

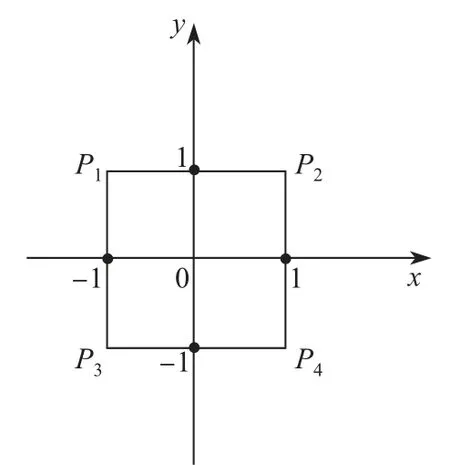
图 1 闭线段PiPj 示意图Fig.1 Diagram of closed segment PiPj

因为

同理可得，

结合

故

因为(0，0) /∈bd M， 故

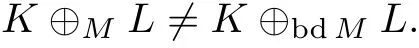
例 3 K = {e1}，L = {e2}，M = [1，3]× [1，3].P1，P2，P3，P4是集合 M 中的点， 坐标分别为 (1，3)， (3，3)， (1，1)， (3，1). 可验证

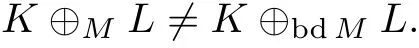
证明 由于(2，2)∈K ⊕ML，(2，2) /∈K ⊕bdML， 证明可仿照例2.

当 M ⊂ Λ1且 M ∈ K2， K，L ∈ Kno时， 有 K ⊕ML=K ⊕bdML. 进一步研究 K ⊕ML 和K ⊕extML 是否相等时， 发现在相同的约束下， K ⊕ML 和 K ⊕extML 不一定相等.

例 4 如图 2 所示， 在 R2中， K =B+e2，L=B+e1， 其中 B 是以原点为中心， 1 为半径的单位球， e1= (1，0)，e2= (0，1).M = △OP1P2， 其中 P1= (0，1)，P2= (1，0)，O = (0，0). 下证 K ⊕ML ／=K ⊕extML.

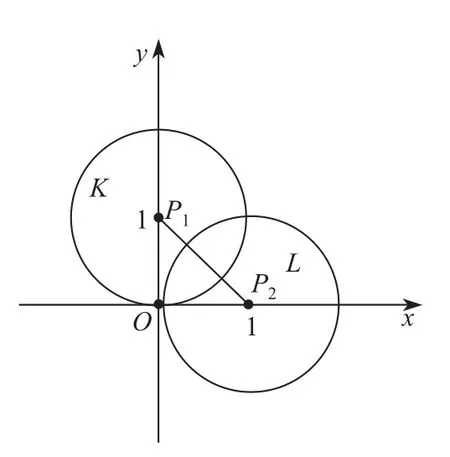
图 2 K， L， M 表示图Fig.2 Diagram of K， L and M

证明 显然 M 的极值点 ext M ={O，P1，P2}. 一方面， 因为

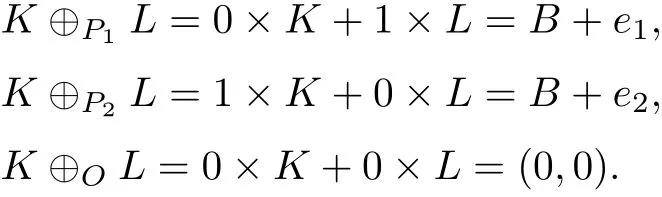
结合

故

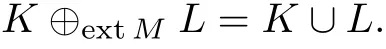
另一方面， 线段 P1P2⊂ M， 设 P1P2上的点坐标为 (a，1-a)，0 ≤ a ≤ 1. 故

由于

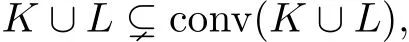
故

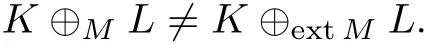
虽然没有得到K ⊕ML 和K ⊕extML 相等的充要条件，但在相同的限制下仍有K ⊕ML=conv(K ⊕extML)成立(定理 4).

引理 6[10]对 M ⊂ Rm，A1，A2，··· ，Am⊂ Rn，

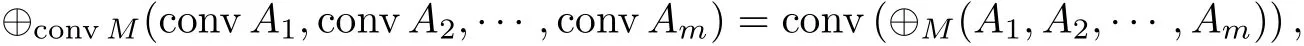
当且仅当M 被包含在Rm的某个闭象限中.

定理 4 当 M ⊂ Λ1且 M ∈ K2， K，L ∈ Kn时，

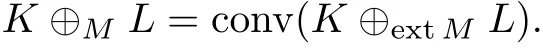
证明 由引理3 知M =conv ext M， 再由引理6 知