运价呈几何布朗运动规律的班轮运输期权决策

宋 巍，刘李鹏，杨华龙，王大元

(大连海事大学 交通运输工程学院， 辽宁 大连 116026)

集装箱运输是国际工业品贸易的主要运输方式，在国际海运班轮市场中占有重要地位。[1]为满足客户的需求，船公司(承运人)需在固定的航线上，按特定的发船频率和船舶挂靠港口顺序，以公布的船期为托运人提供规则的集装箱班轮运输服务。[2]受船舶运力固定、运输服务不可存储、固定成本高和边际成本低等因素的影响，为提高舱位利用率和运营效益，承运人通常采取与货运代理人或大客户签订长期合同的策略[3]，以较为固定的运价为客户提供集装箱货物班轮运输服务；承运人对大多数普通客户(托运人)采取以包箱费率为主的均一定价[4]，即对托运人的集装箱货物只区分集装箱尺寸和相应的航线，按统一标准计收运费。这种固定或均一的定价越来越不适应当今竞争日益激烈的班轮运输市场。此外，在面对运输需求剧烈波动变化时，这种运价策略缺乏应对的灵活性和有效性。班轮运输期权作为一种新的补充策略已受到承托双方的高度关注，其是将金融衍生工具应用到航运服务市场的产物，既可在远期确定舱位预售量，又兼具应对市场需求变化的灵活性和有效性。[5]因此，研究集装箱班轮运输期权决策问题具有重要的理论和现实意义。

运价是关乎集装箱船公司班轮运输效益的关键指标之一，班轮定价一直是学者们研究的热点问题。代表性的研究包括： GARRIDO[6]考虑到运输需求对运价决策的影响，针对弹性需求的班轮定价问题，通过复式拍卖的方法确定运价，达到提高船公司运输收益的目标；曾庆成等[7]考虑到承、托双方之间的博弈关系，基于差价补偿策略构建序贯决策博弈模型，研究托运人订舱行为和承运人的定价决策；YIN等[8]研究价格折扣对托运人的影响，构建班轮公司的折扣定价模型。这些研究结合运输需求、承托双方的博弈行为特征和运输成本等诸多不确定性影响因素，研究班轮定价问题，但都是在垄断环境下进行的，即运价是由承运人控制且未考虑市场供需变化和未来不确定因素对运价产生的波动影响，因而其适用范围均较为有限。

为研究如何更好地应对未来市场的剧烈波动，专家开始借鉴期权理论在航空领域的研究成果，将其引入到海运领域。例如：文献[9]通过将运费期权引入海运服务市场中，建立托运人收益优化模型，对其在海运服务供应链中的最优化决策进行分析；文献[10]基于期权理论提出国际集装箱海运企业运输协议动态定价的决策方法，建立附带美式认购/认沽期权的国际海上集装箱运输协议动态定价决策模型。这些有关海运期权问题的研究不仅丰富了海运定价策略，而且在一定程度上推动了海运风险的分担和防控。然而，刚刚起步的海运期权问题研究仅考虑托运人(文献[9])或承运人(文献[10])应对市场变化时单方面的决策行为，并没有考虑承托双方的博弈决策行为，这在一定程度上影响了海运期权的实际应用效果。鉴于此，本文将运价作为外生随机变量，通过分析集装箱班轮运输承运人和托运人的博弈行为，构建承运人期权定价和托运人最优期权认购量的Stackelberg博弈模型，在海运运价服从几何布朗运动规律[11]的条件下，研究承运人和托运人的最优决策行为，以期丰富和完善集装箱班轮运输的定价理论和实践。

1 问题描述

在集装箱班轮运输的某个港口航线上，承运人通常会将一部分运力以长期合同的方式预售给与其具有长期稳定合作关系的货运代理人或大客户，剩余的运力通过直接售舱方式销售给托运人，或期权等以远期方式销售给托运人。为规避未来市场波动的风险，承运人通过发行期权鼓励托运人在远期市场购买期权运力，并在期权到期日即期市场(简称“即期市场”)销售其余运力。托运人可根据承运人的期权定价，选择在即期市场购买运力或从远期市场上认购期权获得运力。由此可见，集装箱班轮运输期权决策主要涉及承运人与托运人之间的决策。

由于班轮运输垄断性逐渐淡化，运价主要由市场供需状况决定，承运人和托运人都是市场价格的接受者。运输服务是一种在期货市场上的标准商品，由MCCARDIE等[12]和BRENNAN等[13]的分析可知：在期货市场上，标准商品的短期价格服从几何布朗运动规律。此外，KOEKEBAKKER等[14]采用几何布朗运动对运价进行建模，该方法在蒙特卡罗试验中获得了较为准确的结果。据此，本文论述均假定海运运价服从几何布朗运动规律。

基于期权理论，承运人是期权决策的领导者，而托运人是跟随者，承运人与托运人双方形成一个Stackelberg博弈关系。

1) 承运人需推断托运人的期权认购量才能制订合理的期权执行价格和期权费。若期权执行价格和期权费过高，托运人更倾向于在即期市场直接购买舱位；若期权执行价格和期权费过低，托运人会购买并选择执行期权，此时承运人收益会遭受损失。

2) 当承运人给出期权执行价格和期权费之后，托运人需确定合理的期权认购量。期权认购量若过多，则在即期市场运价下跌时，会造成因托运人放弃执行期权而产生期权费损失；期权认购量若过少，则在即期市场运价上升时，会造成托运人的运费增加。

因此，解决集装箱班轮运输期权决策问题的关键是承、托双方在Stackelberg博弈下，承运人制定合理的期权执行价格和期权费，托运人确定合理的期权认购量，以实现承、托双方的利益最大化。

2 期权定价模型

2.1 符号说明

x为单位运力期权执行价格；r为期权费；Q为托运人的期权认购量；D为托运人的舱位需求量；p为即期市场上的单位运价；p0为期初运价；pmax为运价波动上限；pmin为运价波动下限；T为期权到期日；b为单位运输成本；K为承运人在某一港口航线上的运力；m为承运人在即期市场剩余运力的销售比例。

2.2 托运人期权决策

根据海运运价的几何布朗运动规律特征ln(p/p0)～N(μT,σ2T)，ln(p/p0)的概率密度函数为

(1)

式(1)中：μ和σ均为几何布朗运动规律的系数。即期市场上单位运价的概率密度函数为

(2)

当承运人的期权定价为(x,r)，托运人的期权认购量为Q时，托运人的期望运费为

(3)

式(3)中：f(D)为托运人舱位需求量D的概率密度函数；第一项为期权运费；第二项为当市场价格低于期权执行价格时，托运人执行期权时的订舱成本；第三项为当市场价格高于期权执行价格时，托运人在即期市场上订舱的成本。

托运人的期权决策模型M1为

minM1(Q)

(4)

s.t.Q≥0

(5)

Q≤K

(6)

1) 模型M1是一个凸规划。

对式(1)求M1(Q)关于Q的一阶导数和二阶导数，可得

(7)

(8)

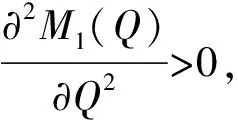
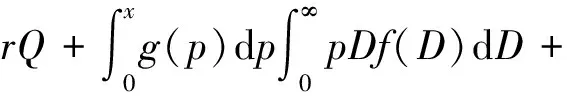
(9)

式(9)中：λ和u为拉格朗日乘子。

模型M1的最优解满足条件为

(10)

(11)

(12)

u,λ≥0

(13)

由此可得：

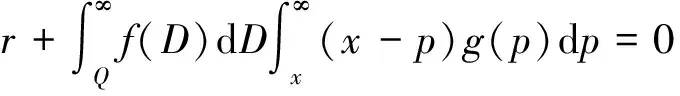
(14)

式(14)中：F(Q)为托运人期权认购量Q的分布函数；F-1(Q)为F(Q)的逆函数。

4) 当λ≠0,u≠0时，式(11)与式(12)矛盾，不存在解。

由于M1是一个凸规划模型，根据库恩塔克条件求得的解即为模型的最优解，可得托运人的最优期权认购量为

(15)

2) 托运人最优期权认购量Q*关于期权执行价格x和期权费r单调递减。

由最优期权认购量Q*满足关系式

(16)

有

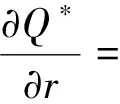
(17)

(18)

由式(17)可知：托运人最优期权认购量Q*关于期权执行价格x单调递减。由式(18)可知：托运人最优期权认购量Q*关于期权费用r单调递减。得证。

2.3 承运人期权决策

承运人在远期市场上以期权的形式销售部分运力，剩余运力只能在即期市场上销售。假设承运人在即期市场的销售比例为m，m是即期市场价格p的减函数，且与承运人的运力规模、服务水平等有关，即

(19)

式(19)中：β为与承运人的运力规模和服务水平等有关的竞争力系数，β∈(0,1]。

考虑托运人的最优期权认购量时，承运人的期望利润为

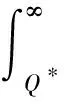
(20)

式(20)中：第一项为期权费用收入；第二项为当期权执行价格高于即期市场价格时，托运人放弃执行期权，承运人在即期市场销售剩余运力获取的利润；第三项为当期权执行价格低于即期市场价格且托运人购买的期权运力能满足需求时，承运人获得的利润；第四项为当期权执行价格低于即期市场价格且托运人购买的期权运力未能满足需求时，承运人获得的利润。

由此可得承运人定价模型M2为

maxM2(x,r)

(21)

s.t.x+r≥pmin

(22)

x+r

(23)

综上，根据承运人与托运人双方之间Stackelberg博弈关系，当承运人给定一个期权定价(x,r)之后，由式(21)可知托运人最优期权认购量Q*是关于(x,r)的函数。因此，将式(15)代入式(21)中，利用模型M2便可求得承运人的最优期权定价，再利用式(15)可求得托运人的最优期权订购量。

3 算法设计

由于定价模型M2的目标函数是一个带有积分的复杂非线性函数，本文设计改进的遗传算法求解。为克服传统遗传算法存在局部搜索能力差、种群多样性逐渐降低和“早熟收敛”等缺陷，本文从2个方面对遗传算法进行改进：

1) 结合适应度定标法和Boltzmann适应度调节策略调节不同时期的选择压力，加大局部搜索能力。

2) 在每一代新种群中定期补充一定数量的新个体，保持种群多样性。

改进的遗传算法步骤如下：

1) 选择编码方式，生成初始种群。本文选择二进制编码方式，并设置最大迭代次数、交叉率和变异率，随机生成初始种群。

2) 适应度评价。为动态调整种群的选择压力，对定价模型M2的目标函数进行线性变化，结合Boltzmann调节策略选择适应度函数

(24)

式(24)中:α为调整参数;W为一个控制参数，随着迭代的进行逐渐变小。记录适应度最优的个体，若种群达到最大迭代次数，则执行步骤7)，否则执行步骤3)。

3) 选择。本文采用轮盘赌法进行选择操作，选择概率由个体适应度决定，适应度低的个体也具有“生存”机会，从当前种群中选择一定比例的个体。同时，采用精英保留策略，使当前代中最优秀的个体保留到下一代，确保种群向高适应度进化。对种群进行选择操作，生成新群体。

4) 交叉。本文采用均匀交叉法，同时为保证种群的多样性和避免过早收敛，在种群中补充新个体，禁止重复个体进行交叉。对种群进行交叉操作，生成新种群。

5) 变异。本文随机选择变异位，然后取反。原基因位值为1，变异为0；反之，原基因位值为0，变异为1。通过变异操作，生成新种群。

6) 局部搜索。本文设计局部搜索算法，运用two-opt对部分个体进行局部搜索，选择最好的个体替换当前个体，以生成下一代。

7) 结束迭代。输出最优个体和解码后的最优结果，得到承运人期权定价结果。

4 算例

为验证所建模型和算法的有效性，本文参照文献[15]，选取某承运人在某个港口航线(起、讫港口)上的运力600 TEU，竞争力系数0.8，单位运输成本680美元/TEU。假设起初运价 795美元/TEU，运价波动下限为600美元/TEU，上限为1 000美元/TEU，托运人的舱位需求量服从均值为30 TEU、标准差为6 TEU的正态分布，期权到期日期为30 d，期权到期日运价的几何布朗运动规律系数μ=0.000 3，σ=0.016 0。算法的主要参数设置如下：种群大小N=80；最大迭代次数GENMAX=80；交叉概率Pc=0.8；变异概率Pm=0.3。算例测试结果见表1。

表1 算例测试结果

由表1可知：承运人采用期权售舱，最优期权执行价格为743美元，最优期权费为55美元，托运人最优期权认购量为24 TEU，承运人期望利润为22 296美元，托运人期望运费为23 711美元。当承运人在即期市场直接售舱时，其期望利润为20 770美元，托运人期望运费为23 894美元。显然，承运人采用期权售舱可增加利润1 526美元，期望利润增长约7.35%；而托运人通过期权获得运力可节省183美元，期望运费节省约0.76%。由此可见，运用期权决策既可增加承运人的期望利润，又可减少托运人的期望运费。

遗传算法收敛图见图1。由图1可知：算法在第15次迭代后搜索到最优值。由此可见，本文设计的改进遗传算法在集装箱班轮运输期权决策问题的求解中具有良好的搜索性能，能搜索到问题的最优解。

由于班轮运输期权决策既与即期市场运价有关，又与承运人的规模和服务水平等市场竞争力因素有关，根据承运人的市场竞争力系数，对期权决策进行敏感性分析，在同竞争力系数下的承运人期权定价和托运人期权认购量变化情况见图2。由图2可知：随着承运人竞争力系数的变大，除承运人的最优期权费保持基本不变以外，承运人的最优期权执行价格会增长，托运人的最优期权订购量相应减少。究其原因，主要是由于承运人在即期市场竞争力越强，其更有能力在期权到期日即期市场直接售舱，减少期权售舱的数量，并提高期权的执行价格，托运人的期权认购量将会减少。

在不同竞争力系数下，采用直接售舱或期权售舱时，承运人的期望利润和托运人的期望运费结果见表2。由表2可知：随着承运人竞争力系数的变大，其市场占有率增大；在期权售舱下，承运人期望利润和托运人的期望运费虽然都会增大，但承运人的利润增长率和托运人的运费降低率会变小。例如：当承运人市场竞争力系数由0.2增大到0.8时，承运人采用期权售舱比直接售舱获得的期望利润增长率由41.47%降为7.35%，托运人的期望运费降低率也从1.19%降为0.77%。承运人在即期市场竞争力越强，其市场占有率越高，期权售舱对承运人和托运人的益处越不明显。

表2 不同竞争力系数下的期望利润和期望运费结果

5 结束语

本文针对运价呈几何布朗运动规律的集装箱班轮运输期权决策问题进行研究，基于承、托双方Stackelberg博弈原理，构建承运人和托运人期权决策模型，并设计改进的遗传算法求解。研究结果表明：应用班轮运输期权决策可提高承运人的期望利润，并降低托运人的期望运费。同时，班轮运输市场竞争越激烈，即承运人在即期市场的竞争力系数越低，采用期权决策，承运人的期望利润越大，托运人的期望运费越低；反之，承运人在即期市场的竞争力系数越大，采用期权决策对承运人和托运人双方的益处越不显著。由此可见，在当今竞争日益激烈的集装箱班轮运输市场环境下，期权决策不仅能抵御集装箱班轮运输需求波动等风险，而且能实现承、托双方的共赢。鉴于班轮运输期权问题的复杂性，本文只研究了单个起、讫港口对航线上的期权决策问题，后续研究将考虑市场竞争环境，研究托运人与承运人之间在整条班轮航线(包含多个起、讫港口)上的期权决策问题应是进一步的方向。