基于数据驱动控制的船舶自动靠泊
2020-12-09余嘉俊牟军敏张本任朱奇舸
熊 勇,余嘉俊,牟军敏,张本任,张 加,朱奇舸
(武汉理工大学 a.航运学院; b.湖北省内河航运技术重点实验室;c.国家水运安全工程技术研究中心, 武汉 430063)
船舶在靠泊过程中,由于受到风、流干扰以及浅水、岸壁效应的影响,会产生复杂的动力学行为,难以精确操控[1],需要通过人的经验来完成靠泊过程。因此,从理论和实践上研究自动靠泊技术具有重要的意义。自动靠泊技术的研究始于20世纪90年代初,杨盐生[2]提出一种靠离泊操纵的数学模型,并设计出计算作用在船体上的流体力及桨力、舵力、拖船力、缆绳和锚链张力的实用算法。卜仁祥等[3]结合增量反馈技术,设计一种无需估计风、流干扰的自动靠泊算法。MIZUNO等[4]在非线性规划最短时间靠泊方法的基础上,改进非线性模型预测控制器。张强等[5]通过总结船舶靠泊技术的发展现状,提出未来船舶自动靠泊的研究方向。闫晓飞等[6]利用三维激光扫描仪工作原理和三维点云数据的处理方法,研发一种能为实现自动靠泊提供航海动态信息的船舶靠泊监测技术。ABLYAKIMOV等[7]提出一种可用于自动靠泊的局部导航测距系统。YANG等[8]设计一种船基绞缆控制装置,可利用分布在艏部和艉部的2根缆绳实现平行靠泊。
船舶在临近泊位时处于低速航行状态,且受到浅水和岸壁效应的影响,难以对船舶进行精确建模,因此基于船舶运动模型的运动控制方法具有局限性,不能满足船舶自动靠泊的要求。国内外学者尝试采用不依赖船舶运动模型的方法来控制船舶的运动。YAMATO等[9]利用ANN(Artificial Neural Network)算法设计靠泊控制器。ZHANG等[10]利用多参数神经网络算法设计在线调参的靠泊控制器。IM等[11-12]和TRAN等[13]利用神经网络设计靠泊控制器,并设计考虑侧推器和拖船等辅助设备的自动靠泊控制器。NGUYEN 等[14]利用自适应神经网络分别训练舵、桨控制信号,由此实现自动靠泊。AHMED 等[15-16]利用神经网络技术并结合虚拟窗口理论设计自动靠泊控制器,采用自由船模试验验证其有效性。张强等[17]使用ANN算法对船舶的自动靠泊控制进行仿真试验。在船舶低速运动控制领域,龚征华等[18]基于喷水推进操舵控制系统的工作原理,设计干扰观测器和全局滑模控制器。VAN等[19]改进ANN算法,并将其应用于实船控制中。
综上所述,船舶自动靠泊方法的研究历史较早,这些方法也很少被应用于实船自动靠泊,且现有的不依赖船舶运动模型的控制方法多为ANN算法,还停留在仿真阶段。在实际的船舶靠泊过程中,该方法的实时性难以保障,较难获得参数训练的样本,而船舶在靠泊过程中允许的控制收敛时间较短,使人工神经网络控制方法难以应用于船舶实际靠泊中。为此设计一种基于船载微波雷达阵列,检测船舶与泊位岸线的相对位置和姿态,并采用基于数据驱动控制的无模型自适应控制方法以实现船舶的靠泊控制,并通过实船试验验证该算法的可行性和控制效果。
1 自动靠泊系统的硬件设计
船舶的自动靠泊需以试验船舶作为载体,完成试验船舶的硬件设计,然后搭建自动靠泊系统试验平台,通过设计试验验证系统的适用性,各模型、算法的稳定性和可靠性,其中船舶硬件设计是实现船舶自动靠泊的基础。船舶自动靠泊的硬件结构主要由以下3个单元组成。
1.1 姿态传感器
船舶在靠泊过程中需获取船舶的实时姿态信息。采用高精度惯导模块,为船舶的自动靠泊提供X、Y和Z等3个方向上的加速度值、角度值和角速度值。
1.2 电子航向仪
船舶在水面航行时,需通过设备获取当前所在位置的经纬度数据,同时需判断其当前的方位和航向,采用电子航向仪实时获取全球定位系统(Global Positioning System,GPS)的数据和航向角数据,利用解析后的数据对船舶进行位置监测和靠泊控制等。
1.3 微波雷达
船舶自动靠泊不同于传统的船舶运动控制,靠泊时距离岸线较近,精度要求较高,因此采用微波雷达阵列来辅助船载GPS进行高精度定位。在船体上分别安装6个微波雷达(见图1),通过各微波雷达采集到的距岸线距离来计算船舶的精确位置和GPS数据,完成船舶的精确定位,并结合船载姿态传感器精确计算出船舶的姿态。
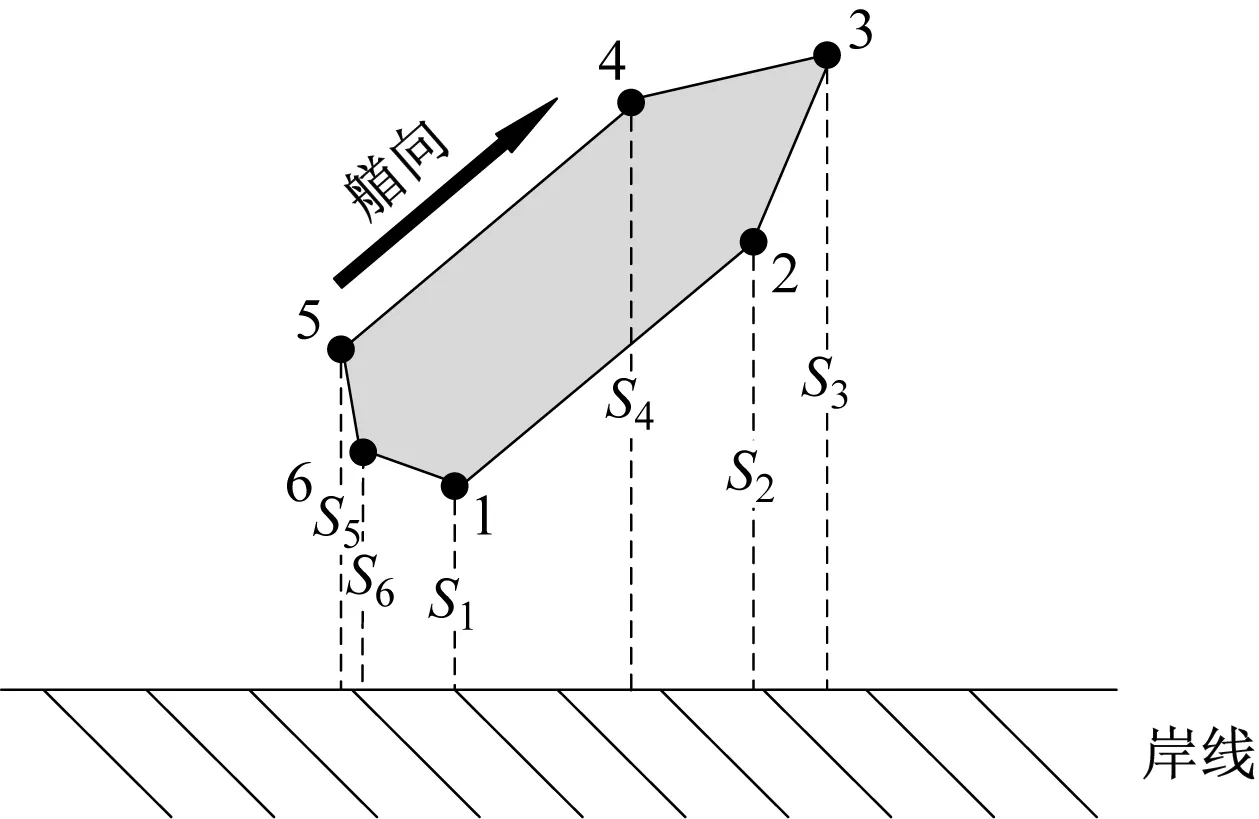
图1 船载微波雷达示意
图1中:S1~S6为各微波雷达距岸线的距离,根据船上各微波雷达的具体位置,结合船载GPS设备精确定位船舶的位置。同时,通过各船载微波雷达测得的距岸线的距离,结合船舶上电子航向仪获得的船舶艏向角判断船舶当前的姿态。
2 船舶自动靠泊流程设计
本文研究的是在静水条件下的船舶自动靠泊问题,船舶在自动靠泊过程中,需根据船舶的各项参数定义其靠泊状态。
2.1 船舶靠泊规则
船舶的靠泊过程可分为船舶抵达泊位前的运动过程和船舶从泊位前向码头靠拢的运动过程2个阶段。
船舶在水流平缓、风力较小、码头下方水域宽阔的条件下航行时,应至少保持与码头1.0~1.5倍船长的安全横距。慢车航行,当艏向与码头下端点距离为2~3倍船长时停车,用舵机使艏艉线与码头外延长线夹角不大于15°,借助船舶惯性滑行前进。[20]
2.2 船舶靠泊的数学定义
在船舶靠泊规则的前提下,定义船舶在靠泊的过程中要实现靠泊,需满足
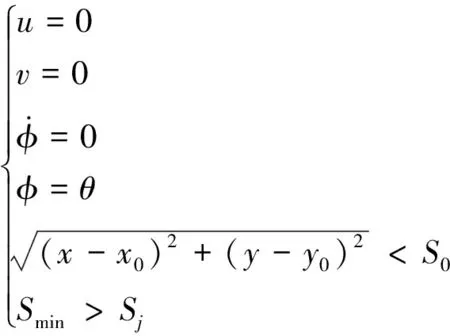
(1)
船舶最终的靠泊状态如式1所示,船舶姿态角为固定值;船舶到达泊位(即船舶重心距泊位小于阈值S0)。在船舶的靠泊过程中,保持船舶边界距岸线始终大于固定值Sj,Smin为各微波雷达采集到的距离信息的最小值。
2.3 船舶自动靠泊整体流程
利用船载电子航向仪和微波雷达阵列获取船舶各微波雷达距岸线的距离,并结合船舶的GPS数据判断船舶相对于泊位的位置,进而得到船舶相对岸的姿态。利用微波雷达和姿态传感器实时反馈船舶的位置信息和姿态角,根据上层的调度算法,并结合下层的无模型自适应控制算法实现船舶的自动靠泊,见图2。

图2 船舶靠泊流程图
自动靠泊算法结构分为上层的靠泊调度算法和下层的运动控制算法。由上层的调度算法计算出船舶目标航向角和航速,由下层的运动控制算法计算出船舶当前指令舵角信息和指令螺旋桨转速信息,从而实现航向和航速控制,完成自动靠泊。
3 船舶自动靠泊调度算法
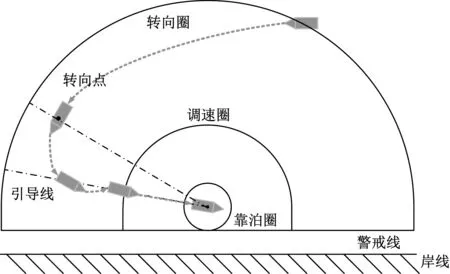
根据《船舶操纵》中的船舶靠泊规则,本文采用的路径规划算法将船舶自动靠泊分为2个阶段,其中:第一阶段是将船舶行驶至设定的转向点处;第二阶段是船舶到达转向点后调整船舶的姿态,并将其沿着引导线驶入泊位。
各微波雷达距离岸线的距离分别为S1~S6,各雷达距离岸线最近距离为Smin,船舶各雷达距岸线的警戒距离为Sj(1.5倍船长),船舶进入该范围时,立即向反方向航行,远离岸线;转向圈半径为Sz(10倍船长),船舶在进入转向圈时转向,先向设置的转向点运动,当船舶到达转向点后,调整航速至5 kn。调速完成后,调整航向,使船舶到达引导线上,再将其艏向角调整为θ(10°),沿着引导线航行,并保持航速为4~5 kn;调速圈半径为St(4倍船长),船舶在调速圈中开始减速至1~2 kn,并保持艏向角为θ,使得船舶缓缓驶入泊位;靠泊圈半径为S0(1倍船长),当船舶进入靠泊圈时,调整姿态,关闭电机,使得船舶到达泊位,即认为船舶完成靠泊操作。引导线与岸线的夹角为θ,转向点位于引导线上距泊位中心8倍船长的位置。船舶靠泊各项阈值示意见图3。

图3 船舶靠泊各项阈值示意
以下为船舶分别从左侧和右侧自动靠泊时的具体流程。
3.1 船舶左侧靠泊
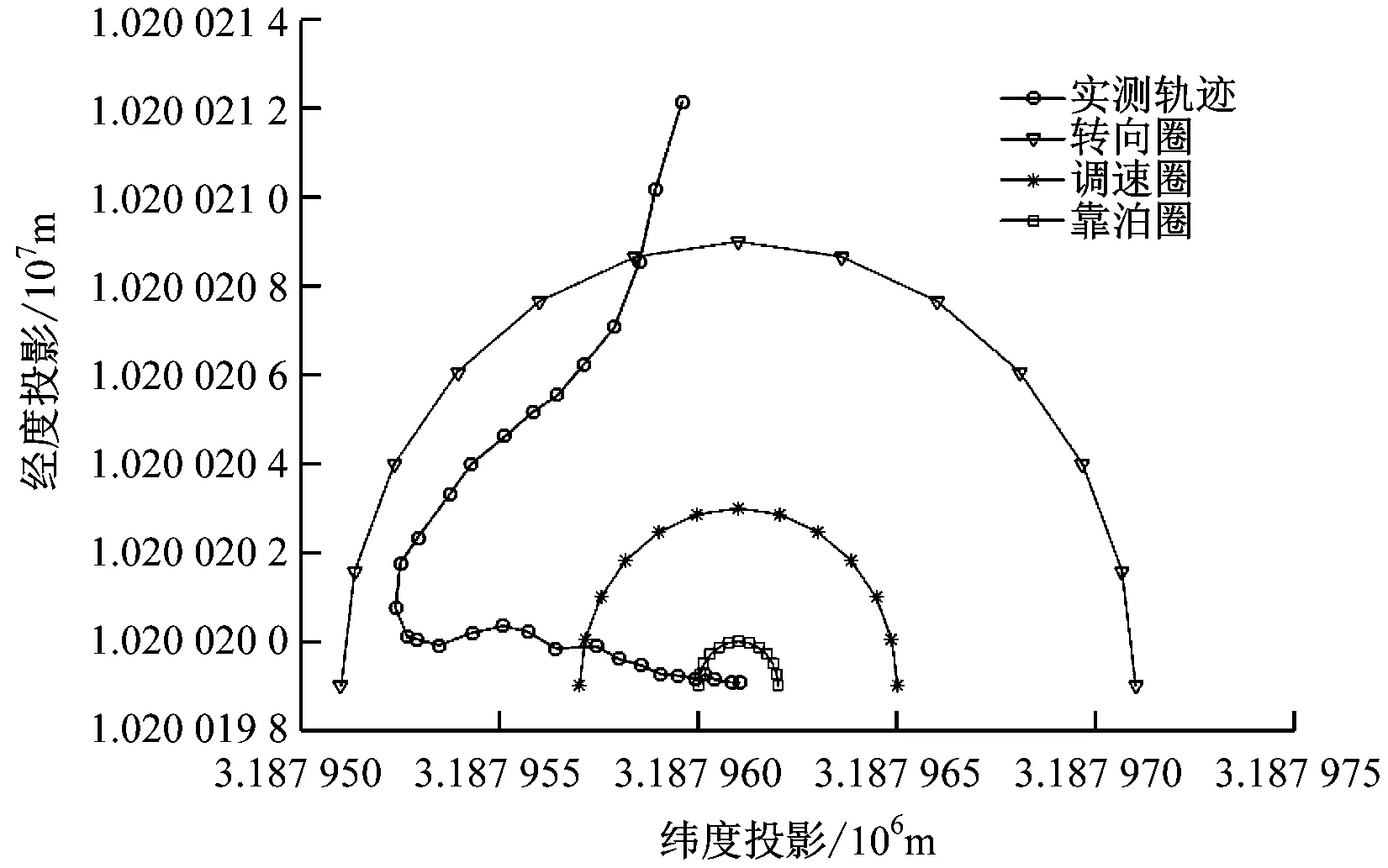
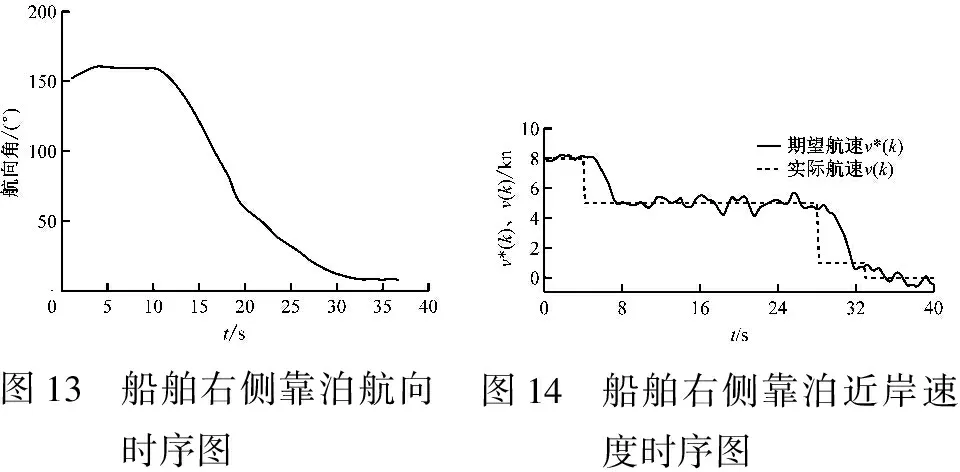
当船舶从左侧靠近转向圈时(见图4),先通过船舶上GPS数据计算出船舶与泊位中心的距离S。当S>Sz(船舶在转向圈外)时,船舶正常向泊位行进;当St 图4 船舶左侧靠泊示意 图5 微波雷达航向调节示意 以Smin=S4为例,当前船舶姿态与定义的靠泊姿态有较大的差距,见图6。靠泊调度算法将大角度左转的控制指令输出到船舶的航向控制器中,完成调向后,继续根据微波雷达的实时数据对船舶的当前姿态进行判断,直至船舶满足靠泊姿态要求。 图6 微波雷达转向示意 调整好船舶姿态后进入调速圈(Sk 当船舶从右侧靠近转向圈时,先算出船舶距泊位中心的距离S。当S>Sz时,船舶正常向泊位航行;当St 图7 船舶右侧靠泊示意 在自动靠泊过程中,需要设计船舶航向和航速2个控制器。 船舶在自动靠泊过程中,会有高速和低速运动2种情况,船舶在低速航行时,较难建立船舶运动模型,从而影响船舶运动控制的精度。数据驱动控制不基于机理模型,而是仅利用被控对象的输入和输出数据实现控制器的设计。[21]因此,在靠泊过程中,采用数据驱动控制分别设计船舶的航向和航速控制器。 考虑一般的离散时间下的非线性系统为 y(k+1)=f(y(k),…,y(k-n),u(k),…, u(k-m)) (2) 式(2)中:y(k)为控制器的测量值,即被控系统的输出;u(k)为控制器的输出,即被控系统的控制量,亦为被控系统的输入;k为釆样时间;n和m分别为系统输出和输入的阶数;…为未知的非线性的函数,可代表一般的无噪声干扰作用的非线性系统。对于式(2)表达的非线性受控系统作以下3点基本假设: y(k+1)=φ(k)Δu(k)+y(k) (3) 1) 系统对于输入、输出均可观测,可控制。 3) 系统满足广义Lipschitz条件,即输入变量变化有界,则输出变量变化有界。[21] 在船舶航向控制中,控制器的输入是船舶的目标航向角,输出是船舶的舵角。这2个控制量均满足上述假设。 设计准则函数为 (4) (5) Δu(k-1)=u(k-1)-u(k-2) (6) (7) (8) Δy(k)=y*-y(k) (9) 式(8)和式(9)中:y*为期望的航向角;ρ1和λ1为无模型控制律的控制参数;式(8)为无模型自适应控制的控制律公式,只有1个需要通过输入输出数据进行辨识的参数,即φ(k);u为输出的舵角信息;y为输入的当前航向角。 船舶的航速控制系统也是一个典型的非线性系统,其输入是船舶的螺旋桨转速,系统的输出是船舶的航速。这2个控制量均满足无模型自适应控制的假设。 设计非线性受控系统为 v(k+1)=φ(k)Δn(k)+v(k) (10) 设计准则函数为 (11) (12) Δn(k-1)=n(k-1)-n(k-2) (13) (14) (15) Δv(k)=v*-v(k) (16) 式(15)和式(16)中:v*为期望的航速;ρ2和λ2为无模型控制律的控制参数;式(15)为无模型自适应控制的控制律公式;式(16)只有1个需要通过输入输出数据进行辨识的参数,即φ(k);n为控制器输出,即输出的螺旋桨转速;v为控制器输入,即船舶当前的航速。 试验船舶参数见表1,实船见图8。 表1 试验船舶参数 图8 试验船舶 船舶航向角控制器参数为:ρ1=0.25;λ1=3;η1=0.001;μ1=1。 船舶航速控制器参数为:ρ2=0.2;λ2=2.6;η2=0.001 5;μ2=0.8。 设计2组船舶靠泊试验,分别为船舶位于转向圈外左侧驶向泊位和船舶位于转向圈外右侧驶向泊位。 船舶初始状态为转向圈外左侧,按设计的靠泊算法停在泊位(见图9),船舶左侧靠泊航向时序图见图10,速度变化时序图见图11。 图9 船舶左侧靠泊轨迹图 图10 船舶左侧靠泊航向时序图图11 船舶左侧靠泊速度时序图 船舶初始航向为101.2°,到达转向点后,调整航向,驶向引导线后保持航向角为10°进入调速圈,最终航向角保持约为9°如图10所示。 步长为0.2 s,船舶记录的初始航速约为8 kn(如图11所示),此时无期望航速要求,在8 s后,船舶调整完成航向时根据调度算法,期望航速为5 kn,船舶完成调速后保持5 kn航速继续行驶,在进入调速圈后,调整航速为1 kn,缓慢向泊位靠拢,到达泊位后停止电机运行,完成靠泊。 船舶初始状态为转向圈外右侧,试验中按设计的船舶调度算法,依次进入转向圈、调速圈和靠泊圈,最终停在泊位,完成自动靠泊(见图12),船舶右侧靠泊航向时序图见图13,船舶右侧靠泊近岸速度时序图见图14。 船舶初始航向为151.5°,到达转向点后,调整航向,驶向引导线后保持航向角为10°进入调速圈,最终航向角保持约为9°如图13所示。 图12 船舶右侧靠泊轨迹图 图13 船舶右侧靠泊航向时序图图14 船舶右侧靠泊近岸速度时序图 步长为0.2 s,船舶记录的初始航速约为8 kn,此时无期望航速要求,在大约4 s后,船舶航向调整完成,根据调度算法,期望航速为5 kn,船舶航速调整完成后保持航速为5 kn继续航行,在进入调速圈后,调整船舶航速为1 kn,缓慢向泊位靠拢,到达泊位后停止电机,完成靠泊如图14所示。试验结果表明:船舶在自动靠泊过程中,无模型自适应控制有良好的控制效果,虽然有些许的误差,但考虑到测量设备的精度问题,这些误差也在可接受的范围内,尤其是在船舶即将靠岸时,船舶处于低速状态,但仍有良好的控制效果,能实现船舶的自动靠泊。 本文设计一套自动靠泊算法,基于微波雷达阵列,结合船载GPS数据,在准确获取船舶的实时位置的基础上,使用无模型自适应控制控制船舶航向和航速,从而实现船舶自动靠泊。同时,设计实船试验,证明按本文介绍的船舶自动靠泊算法,试验船舶能完成自动靠泊。本文采用的船舶为小型无人艇,并未验证大型无人艇能否采用该方法完成靠泊,但该方法具有一般性,可为大型船舶的自动靠泊技术研究提供参考。


3.2 船舶右侧靠泊
4 无模型自适应控制
4.1 船舶航向控制器


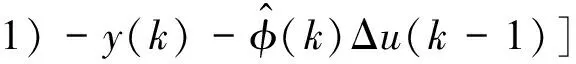


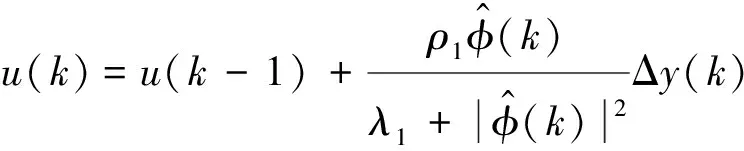
4.2 船舶航速控制器

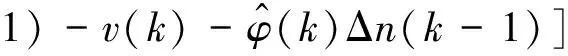

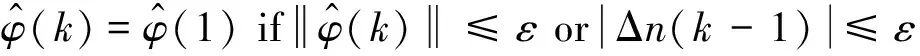
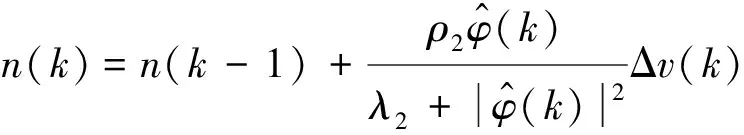
5 实船试验

5.1 船舶左侧靠泊

5.2 船舶右侧靠泊

6 结束语
