定航线下考虑ECA的船舶航速多目标优化模型

甘浪雄，卢天赋，郑元洲，束亚清

(武汉理工大学 a.航运学院； b.内河航运技术湖北省重点实验室， 武汉 430063)

船舶在营运过程中会消耗大量的能源，产生不可忽视的废气排放问题。2016年美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration，NOAA)的研究报告指出：目前每年全球海上船舶排放的颗粒污染物总量相当于全球汽车排放颗粒污染物的50%，每年全球排放的氮氧化物气体中30%来自于海上船舶。[1]针对以上情况，国际海事组织(International Maritime Organization，IMO)于2008年10月通过国际防止船舶造成污染公约(International Convention for the Prevention of Pollution From Ships,MARPOL)(简称《MARPOL公约》)附则VI，提出建立排放控制区(Emission Control Area，ECA)的建议。2018年12月发布的《船舶大气污染物排放控制区实施方案》，将我国沿海和内河水域划为ECA，并给出燃油硫含量的限制。该方案指出,船舶在ECA内航行时应使用含硫量(质量分数,下同)不高于0.1%的轻质燃油。轻质燃油的价格通常远高于船舶使用的重油价格，这意味沿海航行船舶的营运成本将大幅上涨。

目前，多数船公司采用换油的策略应对ECA法规，即在ECA内使用轻质燃油，而在ECA外使用普通的重油。此外，在船舶航行过程中，船舶航行单位时间内的耗油量与航速的三次方成正比[2]，降低航速可有效减少燃油消耗和污染物排放。因此，在一定的时间限制下，在ECA内降低航速，相应地在ECA外加速可有效减少船舶的营运成本。然而，降低航速会增加航行时间,从而导致租船成本增加，单位时间增加的贸易吞吐量的经济附加值下降，同时,延误交货的概率增大。因此，在进行航速优化时，船舶降低营运成本和航行时间是2个互相冲突的目标，需要建立一种有效折中的航速优化方案，以合理降低船舶的营运成本和航行时间。

现有的航速多目标优化方案大都没考虑ECA法规，因此难以实施现有的减排政策。另外，海上气象条件(风向、风速等)会在一定程度上影响航速多目标优化决策，现有优化方案对此欠缺考虑。综上，针对现有研究缺乏考虑ECA法规的问题,基于船舶营运成本和航行时间，综合考虑ECA和气象条件的影响，建立一种综合考虑ECA和气象条件的航速多目标优化模型,以满足ECA法规背景下船公司对经济效益和时间效益的需求。

1 模型建立

1.1 船舶营运成本模型

船舶营运成本主要包括主机燃油成本和与时间成正比的财务项目、折旧费用和船员工资等。

1.1.1燃油成本

由于船舶在ECA内使用的燃油单价CE高于控制区外的燃油单价CN,因此燃油成本为2种燃油的成本之和,即

(1)

式(1)中:QE(vi)为低硫燃油消耗量,QN(vi)为重油消耗量。QE(vi)和QN(vi)可通过以下模型计算[3]

(2)

(3)

(4)

P=ω(Ps+Pw+Pd)

(5)

(6)

(7)

(8)

式(2)～式(8)中：vi,E、vi,N、Di,E和Di,N分别为航段i的ECA内航速、ECA外航速、ECA内航程和ECA外航程，在ECA内vi=vi,E，在ECA外vi=vi,N；K和P分别为船舶主机燃油消耗率和主机功率；Ps、Pw和Pd分别为静水中的主机功率、克服波浪消耗功率和克服风力消耗功率；ω为螺旋桨推进效率；Cts、Cw、Cd、ρ和ρd分别为静水阻力系数、波浪阻力系数、空气阻力系数、水密度和空气密度；S、M和tDW分别为湿面积、货物重量常数和船舶载重量；H1/3、B和L分别为有效波高、船宽和船长；u、ud和A分别为波速、风速和船舶受风面积；vd为设计航速；η为航速是vd时的推进效率；a=0.3,β=0.7;r为波浪系数。

1.1.2单位时间成本

单位时间成本主要包括财务项目、折旧费用和船员工资。

(9)

式(9)中：δ为船舶每天的固定成本。

1.1.3营运成本目标模型

船舶总运营成本是燃油成本和单位时间成本的总和，即

minF1=C1+C2=

(10)

约束条件为

(11)

vi,E,vi,N∈[vmin,vmax],i=1,…,n

(12)

式(11)和式(12)中：t为最大总航行时间；vmin和vmax分别为航速的最小值和最大值。

1.2 船舶营运期间航行时间模型

船舶营运期间的航行时间取决于航程和航速,即

(13)

约束条件如式(11)和式(12)所示。

1.3 多目标优化模型

针对船舶营运成本和航行时间2个冲突的目标,在考虑ECA的影响下建立多目标优化模型。对于m个目标函数的多目标优化问题[4]，通常有

(14)

s.t.:{x∈R|gk(x)≤0(k=1, …,P),

ht(x)=0(l=1,…,Q)}

(15)

R={x:xL≤x≤xU}

(16)

多目标优化问题中1个目标性能的改善可能会引起其余多个目标性能的下降，因此各目标不可能同时达到最佳，只能在这些目标之间权衡和折中。

2 求解算法和流程

如何有效平衡船舶营运成本和航行时间是船公司面临的重要问题之一。以往研究[5-9]表明求解多目标优化模型主要有2种方式:通过线性加权的方法，将多目标优化问题转换为单目标优化问题，进而求解出一组最优解;利用非支配排序的方法，结合启发式算法求解，结果是一组最优解集。

由于人工设置的权重较为主观，因此本文采用基于非支配排序的启发式方法。

基于精英策略的非支配排序的遗传算法(Nondominated Sorting Genetic Algorithm Ⅱ,NSGAⅡ)作为一种较为成熟的多目标寻优算法，相比其他多目标启发式算法，得到的非劣解在目标空间内分布均匀，收敛性和鲁棒性好。[10]因此，本文采用NSGAⅡ算法求解船舶营运成本和航行时间的Pareto最优解集，在此基础上,采用模糊隶属度函数法,从Pareto最优解集中筛选出最佳的折中解。

2.1 NSGAⅡ

NSGAⅡ是一种基于精英策略的非支配排序的多目标遗传算法，其步骤如下：

1) 种群初始化，根据问题范围和限制条件随机初始化种群，种群大小为N。

2) 计算种群内所有个体的适应度值。

3) 快速非支配排序，并根据个体的非支配等级对种群进行分层。首先找出群体中的非支配解集，记为第1非支配层irank=1，(irank为个体i的非支配值)，将其从群体中除去，继续寻找群体中的非支配解集;然后令irank=2,重复上述操作，直到后续每一个非支配层级被找到。

4) 个体i的拥挤度是目标空间上与i相邻的2个个体i+1与i-1之间构成矩形的周长,即拥挤距离。

5) 拥挤度比较算子，此时种群中的每个个体都有非支配层级和拥挤度2个属性。在对2个解进行排名时，优先选择非支配层级较低的解，若2个解属于同一个非支配层级，优先选择拥挤度较大的解。

6) 组合与选择，父代种群和子代种群结合构成新的种群，新种群大小为2N，并通过个体选择来设置下一代种群的个体。当第1非支配层级中个体数小于N时，由下一非支配层级中的个体依次补充，直到种群规模超过目前的种群规模N为止。

7) 选择、交叉和变异操作,根据非支配关系和个体的拥挤度选取合适的个体组成新的父代种群,通过遗传算法的基本操作产生新的子代种群。依此类推，直到满足程序结束的条件。

2.2 模糊隶属度函数

采用NSGAⅡ算法求得的最终结果是一组Pareto最优解集，需要进一步从中找到船公司所需的最佳折中解。本文建立一种模糊隶属度函数，进而确定最佳折中解。

令fi,max和fi,min分别为Pareto解集中目标函数的最大值和最小值，定义目标函数对非支配的一组解vj的满意度为γi,j,有

(17)

将满意度γi,j归一化,可得

(18)

式(20)中：M为目标个数；Z为Pareto解集中解的个数。

2.3 求解过程

1) 由于船舶营运成本和航行时间的量纲与数量级不一致，因此先运用max-min归一化的方式对2个目标函数进行处理，i为第i个目标函数,有

(19)

2) 生成随机规模为N的种群，每个个体的染色体即为对应的1组可行解。同时,定义最大迭代次数tmax等参数。

3) 根据式(10)和式(13)计算个体对应的营运成本和航行时间的目标值。

4) 比较同一代个体之间的适应度值，保留不被支配的解;将不被支配的解与历史非支配解相对比，若历史非支配解不被新的个体支配则保留，若被支配则进行替换，彼此互相不支配则随机选择。

5) 合并非支配的父代和子代，进行选择、交叉和变异操作。

6) 判断迭代次数是否小于最大迭代次数，若是,则返回步骤继续迭代，否则输出Pareto最优解集。

7) 根据船舶参数分别计算出船舶营运成本和航行时间的最大值F1,max、F2,max和最小值F1,min、F2,min，结合式(17)和式(18)计算出Pareto解集中各解的满意度。

8) 满意度最大的解即为最佳折中解。

求解流程见图1。

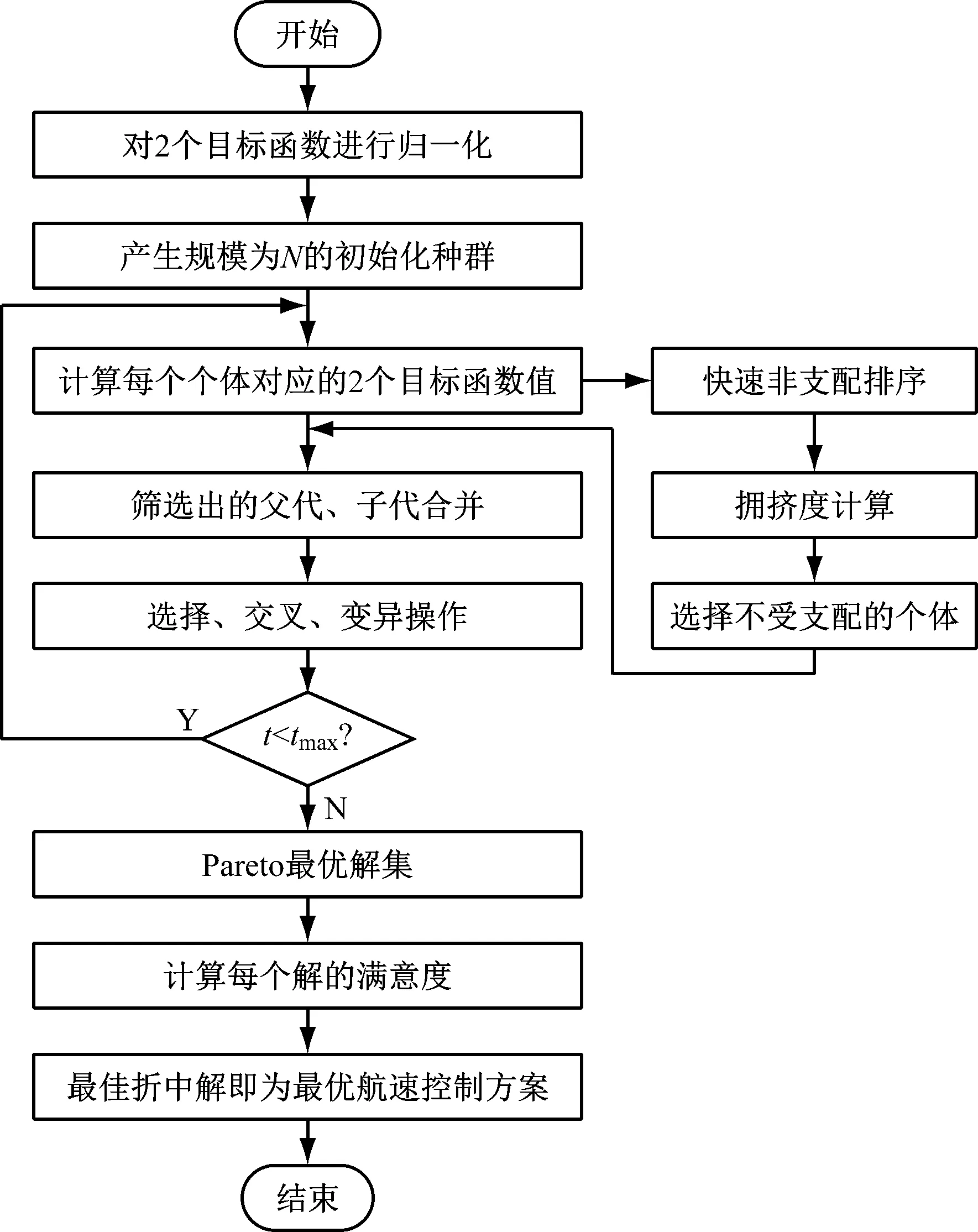
图1 求解流程

3 案例分析

3.1 案例概况

为验证该航速优化方案的有效性，以1艘45 000 t的散货船为例，选定2018年06月08日09:08—2018年06月10日17:30由上海港至营口港的航线进行案例分析。实际航线和实测的气象条件信息分别见图2和图3,对应的航线数据见表1。

3.2 航速优化结果

将气象数据、ECA边界信息、船舶静态数据、航线数据、重油和低硫燃油市场油价数据输入建立的航速多目标优化模型。对应的Pareto最优前沿见图4。由图4可知:该算法可有效折中船舶营运成本和

图2 上海港至营口港航线示意

a) 风速

c) 波速

航行时间2个目标，得出权衡之后的航速优化控制方案。相应的航速优化结果见表2。由表2可知:当船舶以优化航速航行时，相比实际情况可节省1 524美元的营运成本，可减少约1.5 h的航行时间。若该船1 a执行30次该航行任务，能节省超过45 000美元的营运成本，减少约45 h的航行时间,对于船公司而言经济效益相当可观。

有效折中的航速优化控制方案见图5。由图5可知:成本下降主要是由于船舶在ECA内减速，从而有效减少价格较为昂贵的低硫燃油的消耗量。此外，船舶在ECA外加速，能保证船舶运营效率。

表1 给定航线的实船数据

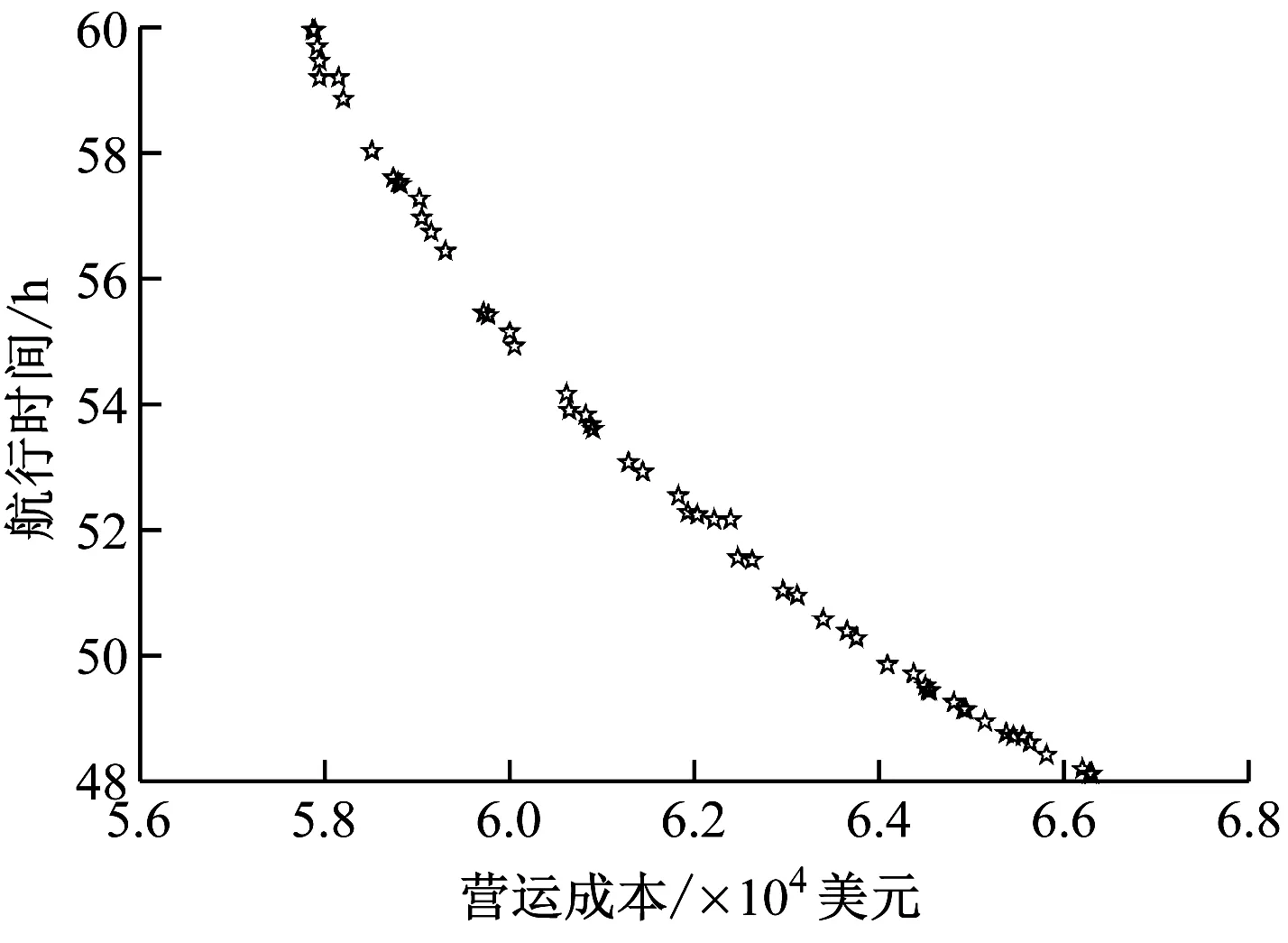
图4 船舶营运成本和航行时间的Pareto前沿

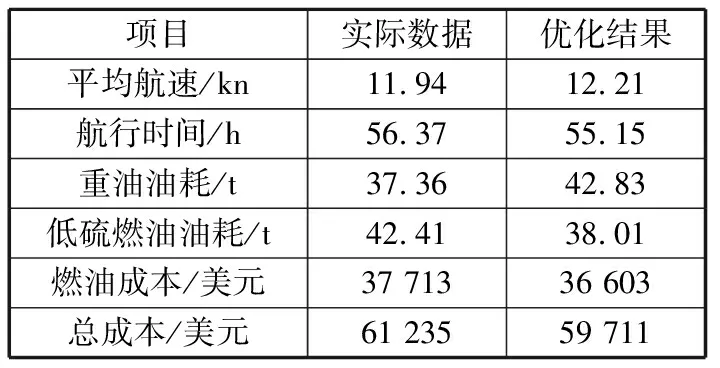
表2 船舶航速多目标优化结果

图5 有效折中的航速优化控制方案

4 结束语

针对船舶营运成本和航行时间2个冲突的目标，在考虑ECA的影响下,建立一种综合考虑ECA和气象条件的航速多目标优化模型。运用NSGAⅡ算法求出降低营运成本和减少船舶航行时间2个目标的Pareto最优解集;在此基础上,采用模糊隶属度函数法,从Pareto最优解集中筛选出最佳折中解。以我国沿海一艘散货船运营航线为例,对建立的模型进行仿真计算，结果表明:求解算法能有效求出相应气象条件下的船舶最佳折中航速，当船舶以优化航速航行时，可有效降低船舶营运成本，缩短船舶航行时间，给船公司带来可观的收益。通过降低航速可有效权衡船舶营运成本和船舶航行时间2个目标，有效实现航运低迷背景下经济效益的最大化。