Ti-Al-Nb 合金的热变形与动态再结晶行为研究

亓耀国，郭子鹏，王兆天，刘延辉,2，宁永权

（1.西北工业大学 材料学院，西安 710072；2.陕西科技大学 机电工程学院，西安 710021）

随着航空航天、车辆、舰船等发动机性能的不断提高，对高温结构材料的性能提出了越来越高的要求。常规的高温合金不仅密度较高，而且其使用温度也已接近目前先进发动机各主要零部件的使用极限。与传统的金属材料相比，金属间化合物材料的强度、硬度、抗蚀和高温性能等颇佳，可补充传统金属材料的不足，成为近年来重点开发应用的新型结构材料。据推测，下一代飞行器发动机中质量占20%以上的部件均可能采用金属间化合物制造[1—2]。

Ti3Al 基合金是一种金属间化合物，具有较高的高温强度、比弹性模量、抗氧化性能以及密度小、比强度高的特点，同时它还具有较好的蠕变抗力等，与钛合金和镍基合金相比优势明显，因此引起了材料科学界的极大兴趣，Ti3Al 基合金将应用于航空航天、能源等高科技领域，极其适合在600～750 ℃环境下工作，代替钛基合金可提高结构的使用温度，且构件可减轻40%左右，从而对增强航空发动机推重比具有重要的意义。从20 世纪50 年代开始，一些国家就展开了Ti3Al 基金属间化合物的研究，但由于脆性问题迟迟未被突破，曾一度处于低潮。此后一些年，很多国家在克服Ti3Al 基合金的室温脆性方面做了大量的研究，主要是添加Nb 元素[3]。

美国已将Ti3Al 基合金应用于制造喷气发动机的尾喷燃烧器、高压压气机机匣与航空发动机后几级压气机转子等结构；日本已将Ti3Al 基合金应用于制造汽车关键零部件，我国在相关领域将Ti3Al 基合金用于制备关键结构件，如涡轮壳体组件、发动机键零部件、支承环等[4]。

材料在热加工过程中通过动态回复及动态再结晶细化晶粒，改善显微组织及力学性能。Ti-14Al-21Nb是Ti3Al 基合金的一种新型钛合金。目前研究主要关注Ti-14Al-21Nb 合金的机械加工性能，而对其动态再结晶演变规律研究较少[5]。

1 试验

1.1 材料及方法

Ti-14Al-21Nb 相变温度为1160～1180 ℃，最高工作温度可达700～800 ℃，综合性能良好[6]。将棒状材料制成Ф8 mm×12 mm 的试样，在Gleeble-1500 热模拟机上完成热压缩试验。把试样加热至设定温度，保温3 min 之后进行等温变形，结束后喷液冷却。应变速率分别为0.005，0.05，0.5，5 s−1，变形温度为1353，1383，1413，1443 K，变形量为50%。

1.2 结果

不同变形条件下Ti-14Al-21Nb 合金的真应力-应变曲线如图1 所示分为2 个阶段。首先以加工硬化为主，流动应力增大至临界值，在各温度下的应变速率为0.005 s−1和0.05 s−1时，此临界值为其应力峰值，应变速率为0.5 s−1和5 s−1时先经过初始应力后，应力与应变关系呈正比然后达到峰值；其次，在各温度下达到峰值应力后，应变速率为0.005，0.05，0.5 s−1时，随应变增大应力逐步降至某一稳定值，应变速率为5 s−1时应力随应变的增加逐步下降。

由图1 可知，变形温度一定时，应变速率越大，应力值越高；应变速率一定时，变形温度越高，应力值越低。随着变形温度的降低，位错爬升或交叉滑移等位错的运动驱动力减小；随着应变速率的增大，动态再结晶形核、长大的过程所需时间将会减少。变形温度一定时，应力值随应变速率的增大而上升；应变速率一定时，应力值随变形温度的升高而降低。应变速率的增大会导致动态再结晶形核、长大过程所需时间减少；变形温度降低会导致位错爬升或交叉滑移等位错的运动的驱动力减小，这两种情况均会抑制再结晶的形核与长大。

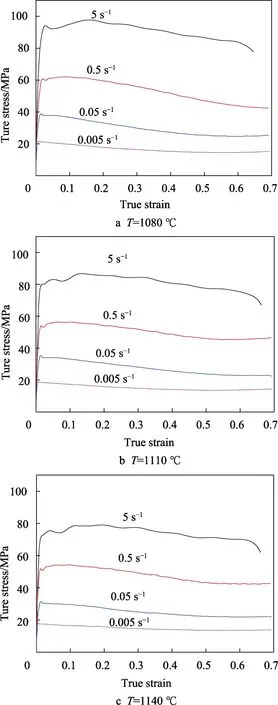
图1 温度及应变速率不同的真应力-应变曲线Fig.1 True stress-strain curves at different temperatures and strain rates

1.3 分析讨论

Poliak 和Jonas[7]等定义加工硬化率θ=dσ/dε，认为动态再结晶发生的临界条件为加工硬化率-应力曲线出现拐点，且一般在峰值应变之前[8]。

图2 为不同变形条件下，在峰值应力出现拐点之前的加工硬化率曲线，说明这些试验条件下试样的动态再结晶均发生在峰值应力出现之前，将得到的临界应变、临界应力列于表1。由表1 可见，随着变形温度的降低与应变速率的提高，钛合金发生动态再结晶所需的临界应变将增大。

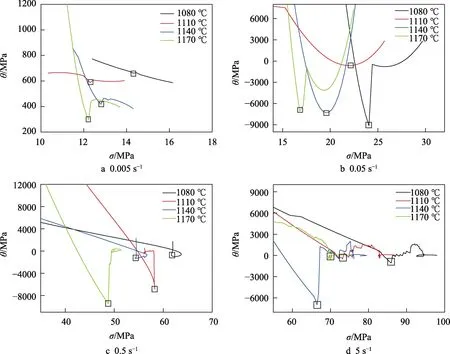
图2 峰值应力出现之前的加工硬化率曲线Fig.2 Hardening rate curve before peak stress

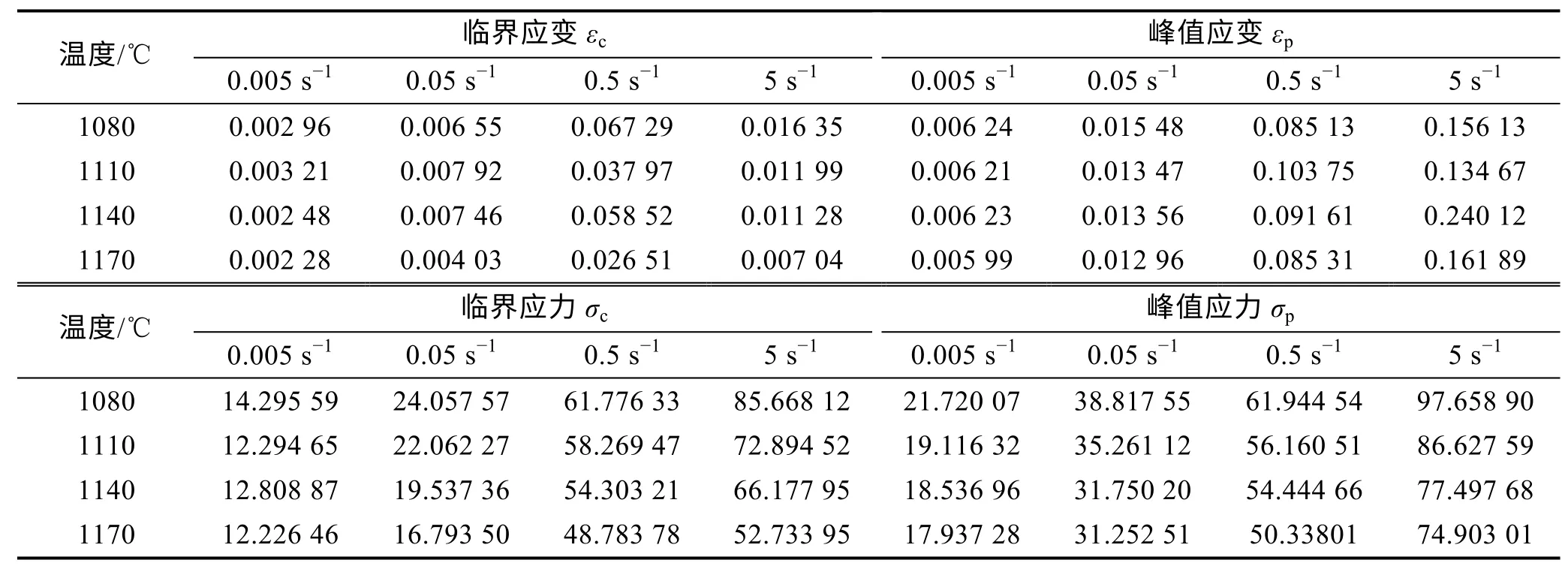
表1 不同变形条件下的临界应变、临界应力、峰值应变、峰值应力Tab.1 Critical strain,critical stress,peak strain,peak stress under different deformation conditions

2 建立模型

2.1 流变应力的本构模型

动态再结晶激活能的大小决定着动态再结晶是否能够发生。文中采用Zener-Hollomon 参数Z来反映变形温度、应变速率之间的关系，然后用双曲正弦函数表征参数Z和流变应力之间的关系式[9—12]：

式中：R为气体常数；T为热力学温度；Q为动态再结晶激活能；F(σ)为应力函数；A，α及n是与材料相关的系数，且α=β/n。将式（3）中应力函数F(σ)代入式（2）中，可得到：

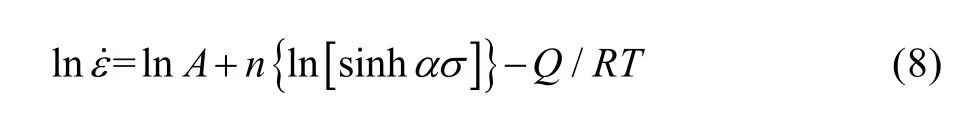
当是一定时，不同的应力状态下，ln［sinhασ］ 与1/T的线性关系如图4 所示，Q/RT为所有斜率的平均值，可求得Q=197.626 kJ/mol。

将所得结果代入式（8）中，得到材料常数A的平均值为3.173×106，因此，，T及σ的关系可用式（9）表示：

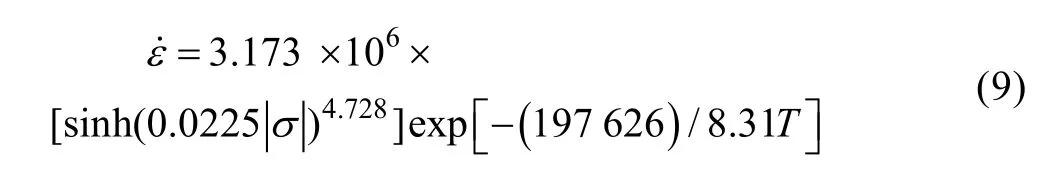
将式（1）代入式（9）中，求得包含Arrhenius项的Z参数流动应力：

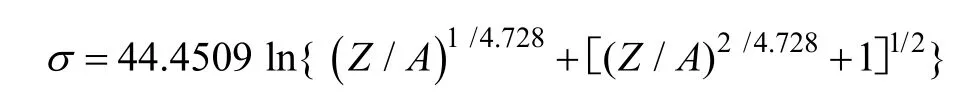
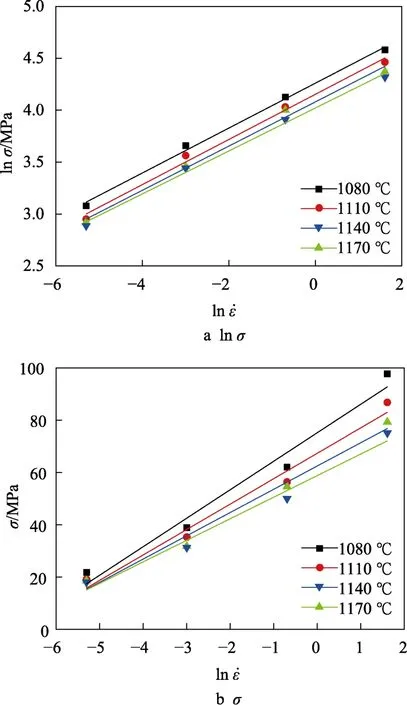
图3 ln σ，σ 与lnε˙的关系Fig.3 Relationship between ln σ,σ and lnε˙

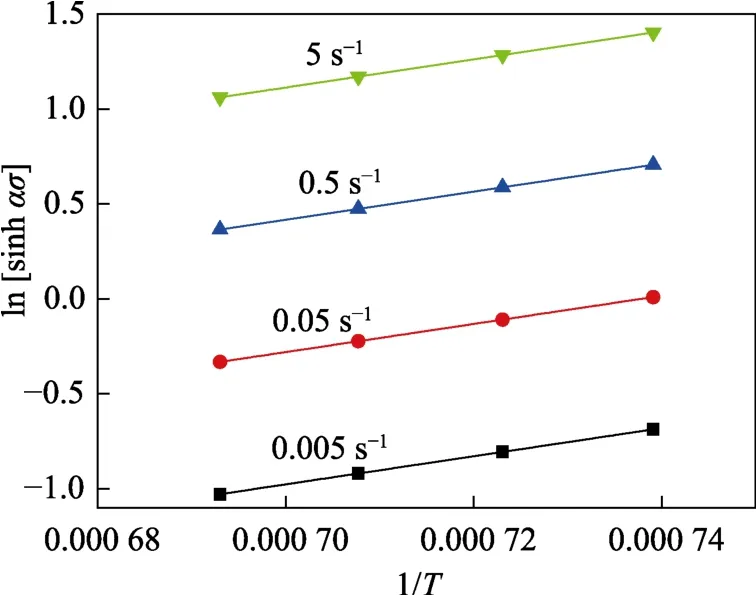
图4 ln[sinh ασ]与1/T 的关系Fig.4 Relationship between ln[sinh ασ] and 1/T

2.2 动态再结晶动力学模型

热塑性变形过程中，临界应变出现前，动态再结晶晶粒将在原始晶粒边界、孪晶界、变形带处形核、长大，位错不断积聚。继续变形，位错增殖（加工硬化引起）及位错湮灭（动态再结晶引起）由始至终存在。当加工硬化的作用与动态软化的影响基本一致时，流动应力值保持不变，变形将处于稳定状态[13]。在本研究中采用与时间呈S 型关系的典型曲线表征动态再结晶动力学演变，在应变速率恒定条件下，时间由应变表示，动态再结晶体积分数由已修正的Avrami 方程表述，因此在高温变形条件下，可由式(10)描述动态再结晶演变的动力学[14]：

式中：XDRX为动态再结晶晶粒的体积分数；m为Avrami 常数，最大软化速率应变ε*在加工硬化率曲线的谷值处，如图5 所示。

在图5 中，应变为5 s−1的加工硬化率曲线在峰值应变之后先上升然后在0 以下波动，动态回复软化作用发挥主要作用；应变为0.5 s−1的加工硬化率曲线呈现先下降再上升的趋势，最后值为负，其加工硬化产生的能量累积被消耗完之后，没有新的能量累积，加工硬化作用较动态回复软化作用更明显；应变为0.005 s−1和0.05 s−1的加工硬化率曲线则呈现明显拐点之后接近于0，此时加工硬化和软化基本相当。

将临界应变εc及由图5 得到的ε*（列于表2），与无量纲参数Z/A联系，利用最小二乘法线性拟合得到图6，可列下式：

假定XDRX=1 代表流动应力达到稳定，然后将与XDRX=1 对应的变形条件带入式（10），得到m的平均值为6.912 02，将动态再结晶动力学模型列于表3。

图5 峰值应力出现之后的硬化率曲线Fig.5 Hardening rate curve after peak stress appears

表2 由图5 得到最大软化速率对应的应变ε＊Tab.2 Strain corresponding to the maximum softening rate ε* from Fig.5

图6 无量纲参数Z/A 与ε*和εc 的关系Fig.6 Relationship between dimensionless parameter Z/A and ε*,εc

表3 基于应力-应变曲线的动态再结晶动力学模型Tab.3 Dynamic recrystallization kinetics model based on stress-strain curve

根据动态再结晶动力学模型，计算变形条件对动态再结晶体积分数的影响，如图7 所示。动态再结晶的体积分数随应变增大至1，证明发生了完全动态再结晶。根据图7 可以看出，当变形温度一定，达到相同动态再结晶体积分数时，应变速率越大所对应应变值越大；当应变速率一定，达到相同动态再结晶体积分数时，变形温度越低所对应应变值越大，说明应变速率的增加及温度的下降都会导致动态再结晶发生延后。动态再结晶晶粒在形核与长大过程中，由于应变速率增大，变形量达到一定程度所需时间缩短，位错回复运动不能充分进行，位错不均匀分布使得应力集中，抑制了动态再结晶的形核速率；而变形温度降低，使合金中位错移动等减少，大量的孪晶、位错难以发生运动，从而不会发生重组，导致材料动态再结晶延后发生。

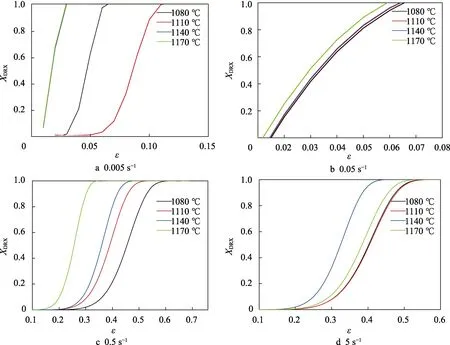
图7 不同温度、不同应变速率下预测的XDRX 体积分数Fig.7 Volume fraction of XDRX predicted by strain rates of 0.005,0.05,0.5 and 5 s−1 at different temperatures

2.3 动态再结晶对应力软化的影响

金属材料发生动态再结晶能够改善其合金组织、提高机械性能。在热塑性变形过程中，当还没有发生动态再结晶时，位错增殖及位错间相互作用导致应力变化较剧烈，在临界应变后新的晶粒形核长大即发生动态再结晶。在随后的变形中，变形不断产生的位错增殖及在热和外力作用下、由动态再结晶引起位错的滑移、攀移并发生合并重组，使材料发生动态软化。当加工硬化的作用与动态再结晶软化的影响相当时，流动应力值不受应变的影响保持稳定，此时动态再结晶晶粒呈现等轴状，并保持一定的大小[12—14]。

如图8a—d 所示，在较大的应变速率下，曲线降到最低点后呈上升趋势，在较小的应变速率下，曲线降到最低点后基本趋于稳定。说明在在高应变速率下材料先经加工硬化，然后软化作用占主导地位；在低应变速率条件下经加工硬化后硬化和软化作用相当，其中软化作用在剧烈变形后的晶粒内，硬化作用于相邻晶粒，同时发生使得呈现一个动态平衡。

图8 动态再结晶对应力软化的影响Fig.8 Effect of dynamic recrystallization on stress softening

3 结论

1）材料在峰值应力出现之前均发生了动态再结晶；在高应变速率下，材料在稳定前会发生强烈的软化，并显现双峰，为动态回复型曲线；在低应变速率下，材料加工硬化和软化作用达到平衡后逐渐稳定，显现单峰，为动态再结晶型曲线。钛合金的流变应力对变形温度与应变速率变化敏感，应力软化作用对应变速率敏感，材料动态再结晶能促进应力软化。

2）通过分析应力-应变曲线获得了Ti-14Al-21Nb合金动态再结晶激活能参数，建立热变形本构模型，获得了动态再结晶演变的动力学Avrami 方程。