斜拉拱式协作体系结构参数变化对受力性能的影响

耿帆

(长沙理工大公路工程试验检测中心， 湖南 长沙 410076 )

现阶段桥梁设计研究中不断突破传统结构形式的约束，力求在桥梁跨度与造型上不断突破，让桥梁与城市文化融合，成为城市的标志性建筑。斜拉拱式协作体系作为一种新型结构体系应用到桥梁建设中，它将拱结构和斜拉索结构体系相结合，充分发挥拱受压、梁受弯、索受拉、塔受压的特点，实现跨径和造型上的突破。已建斜拉拱式桥梁分为两类，一类在主梁上锚固斜拉索，如马来西亚Putrajaya桥；另一类在拱肋上锚固斜拉索，如湘潭市莲城大桥。方磊以莲城大桥为例开展斜拉拱式体系桥梁成桥索力和稳定性研究，对多种优化索力方式进行了对比分析；吕建根等以莲城大桥为例，借助ANSYS建模，分析了斜拉拱式体系桥梁的极限承载能力；王莲香等对Putrajaya桥的结构组成、施工过程进行了详细说明；余海燕以翔凤河桥为例，分析了斜拉拱式结构静力性能与参数的敏感性。该文以莲城大桥为研究对象，通过MIDAS有限元软件建立模型，分析斜拉拱体系结构在活载作用下对材料性质、构件刚度等参数变化的内力、位移响应，为斜拉拱式桥梁设计、施工、运营及维修提供数据支撑。

1 工程概况

莲城大桥采用斜拉拱组合体系，主桥跨度布置为(120+400+120) m，边跨与主跨跨度比为0.3。主桥拱式结构采用飞燕式钢管砼系杆拱桥，主拱采用中承式双肋无铰平行拱，拱轴线形采用7倍抛物线，矢跨比为1/5.19，每8 m布置1道吊杆，共设置39道吊杆。斜拉结构主跨斜拉索锚固在拱肋上，主梁水平以上塔高67.5 m，边跨斜拉索锚固在主梁上，共40对斜拉索。主跨主梁采用钢结构，由3道纵梁、每隔8 m 1道横梁及桥面板构成(见图1)。

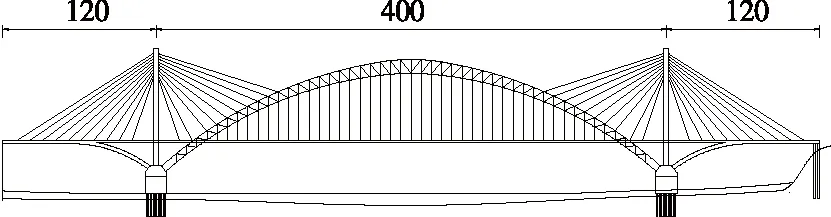
图1 湘潭市莲城大桥(主桥)立面布置示意图(单位：m)

2 有限元模型

采用MIDAS/Civil 2019有限元软件建立空间杆系有限元模型，全桥共建立6 592个单元。斜拉索和吊杆采用桁架单元，其余构件采用梁单元。其中：主拱圈共4 267个单元，拱肋共1 668个单元，主梁共736个单元，斜拉索共112个单元，吊杆共78个单元。模型的边界条件：在桥墩处为固结，边拱支承处为铰接，斜拉索与边拱采用刚臂连接，斜拉索与主拱肋采用共节点模拟。建模时考虑斜拉拱式体系存在的几何非线性因素(见图2)。

图2 湘潭市莲城大桥有限元模型

3 参数变化时结构响应分析

斜拉拱式体系桥主要由主梁、拱肋、吊杆、主塔、斜拉索组成，桥梁施工中主塔和斜拉索可为主拱圈架设提供支承，降低主拱圈架设费用。桥梁运营过程中，充分发挥主拱圈受压、斜拉索受拉、索塔受压、主梁受弯的受力特点，活载由主梁经过吊杆传递到主拱圈，再由主拱圈传递至主塔，其中一部分吊杆竖向力由斜拉索传递至主塔，既减小主拱圈吊杆锚固处弯矩，也降低主塔弯矩，提高体系整体稳定性和拱桥跨越能力。

为探究斜拉拱设计中控制参数，为斜拉拱式桥设计与施工提供优化方案，采用单一参数调整法变化某项参数，识别各参数在结构设计和运营中的敏感性与重要性，进而探究斜拉拱式体系在各阶段的主要受力方式及各构件在荷载作用下的承载能力。

3.1 结构刚度对体系受力性能的影响

分析结构刚度敏感性，采用单一参数调整法控制某一项结构刚度变化，识别结构在承载能力极限状态下的响应，获得结构关键截面的内力、位移(主拱圈截面跨中位移和内力、主梁跨中截面位移和内力、主塔塔顶位移、主塔底部弯矩、斜拉索索力、吊杆拉力)等变化比值，以此反映结构刚度参数的敏感性。

3.1.1 拱肋刚度对体系受力的影响

为识别拱肋刚度在斜拉拱式体系结构中的敏感性与重要性，通过调整拱肋弹性模量为原设计中初始值的0.5、0.75、1.0、1.25、1.5来改变拱肋刚度，获得斜拉拱体系关键截面的位移和内力。选取原设计体系中各关键截面位移和内力作为基本值，获得结构位移和内力与基本值的比值，结果见图3、图4。

由图3、图4可知：拱肋刚度比值在0.5～1.5变化时，拱肋刚度逐渐增加，斜拉拱式体系整体刚度也增加。承载能力极限状态下，拱肋刚度变化对主拱圈跨中截面轴力和弯矩、主梁跨中截面弯矩、跨中吊杆拉力、主塔顶部位移、塔底弯矩的影响很小，结构内力变化在1%以内。随着拱肋刚度的增加，主拱圈跨中截面位移逐渐减小，位移比值由2.02减小至0.67；主梁跨中位移逐渐减小，位移比值由1.45减小至0.85；斜拉索索力也逐渐减小，索力比值由1.10减小至0.96。

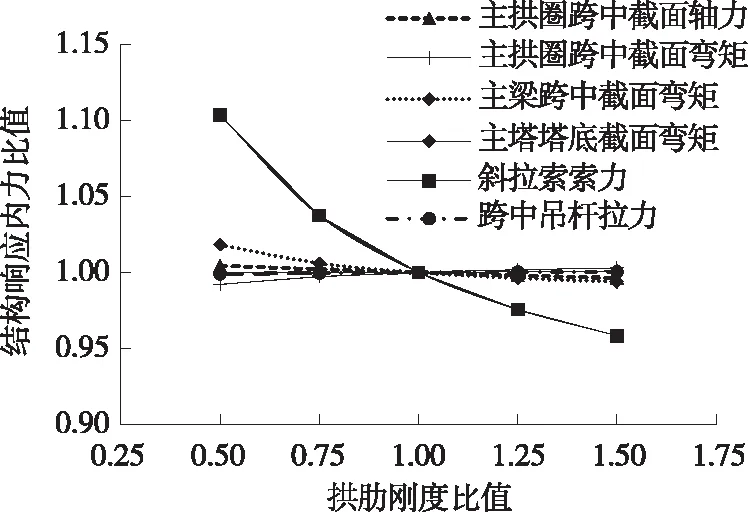
图3 拱肋刚度变化时结构响应内力比值

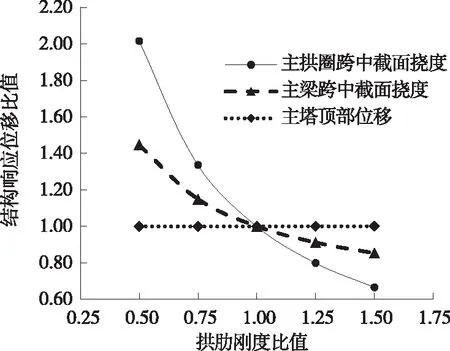
图4 拱肋刚度变化时结构响应位移比值

该桥斜拉拱式体系将斜拉索与主拱圈锚固，斜拉索的内力值与拱肋刚度、位移密切相关，拱肋刚度增加，主拱圈变形减小，从而使斜拉索变形减小、索力减少，符合理论及工程结构响应情况，拱式结构在该体系中作为承力结构。

3.1.2 斜拉索刚度对体系受力的影响

为识别斜拉索刚度在斜拉拱式体系结构中的敏感度和重要性，采用3.1.1节参数设置和分析方法进行研究，结果见图5、图6。

图5 斜拉索刚度变化时结构响应内力比值

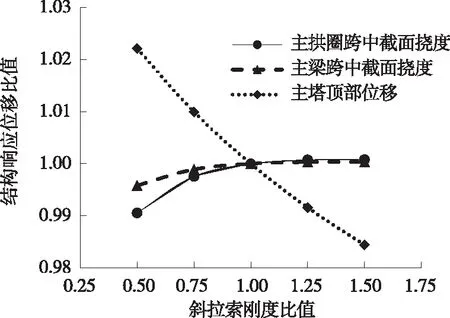
图6 斜拉索刚度变化时结构响应位移比值

由图5、图6可知：斜拉索刚度比值为0.5～1.5时，承载能力极限状态下，主拱圈跨中截面轴力和弯矩、主梁跨中截面弯矩、跨中吊杆拉力、主塔塔底弯矩的变化很小，结构内力变化在1%以内。随着斜拉索刚度的增加，斜拉索索力逐渐增大，内力比值由0.92增加至1.06；主塔顶部位移减小，位移比值由1.02减小至0.98。斜拉索刚度小于初始设计值(刚度比值为0.5～1.0)时，主拱圈跨中截面和主梁跨中截面挠度小于初始设计值，原因是斜拉索锚固于近塔侧1/4拱肋上，斜拉索索力对主拱圈产生一定水平力，使主拱圈跨中截面挠度大于无索时挠度。

由此可见，在承载能力极限状态下，斜拉索刚度参数对斜拉拱式体系整体结构响应及刚度变化的影响不大，斜拉结构在该斜拉拱体系桥梁中承受的荷载比例较小。

3.1.3 主梁刚度对体系受力的影响

为识别主梁刚度在斜拉拱式体系结构中的敏感度和重要性，采用3.1.1节参数设置和分析方法进行研究，结果见图7、图8。

图7 主梁刚度变化时结构响应内力比值

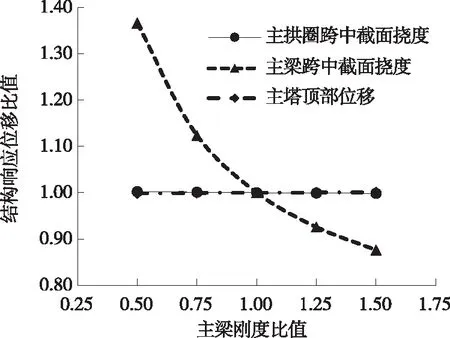
图8 主梁刚度变化时结构响应位移比值

由图7、图8可知：主梁刚度比值在0.5～1.5变化时，承载能力极限状态下，只有主梁结构响应较明显，其他关键截面内力、位移变化量均在1%以内。随着主梁刚度的增加，主梁跨中弯矩逐渐增大，内力比值由0.89增加至1.10；主梁跨中轴力逐渐增加，内力比值由0.60增加至1.39；主梁跨中挠度逐渐减小，位移比值由1.37减小至0.88。原因是拱式结构体系中，主梁在吊杆作用下可近似看作等间距连续梁结构，荷载作用下，吊杆力基本不变，主梁刚度变化主要影响自身受力情况。该体系中拱脚处拱肋与主梁刚接，主梁分担一部分系杆力。

由此可见，主梁刚度参数在承载能力极限状态下对斜拉拱式体系整体结构响应及刚度变化的影响不大，对自身内力和挠度的影响较大。实际工程中主梁需维持一定刚度，以减少主梁挠度，保障行车舒适性。

3.1.4 吊杆刚度对体系受力的影响

为识别吊杆刚度在斜拉拱式体系结构中的敏感度和重要性，采用3.1.1节参数设置和分析方法进行研究，结果见图9、图10。

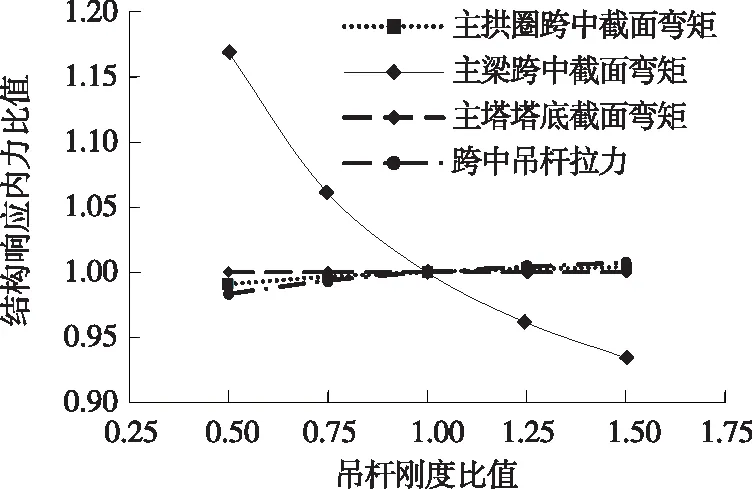
图9 吊杆刚度变化时结构响应内力比值

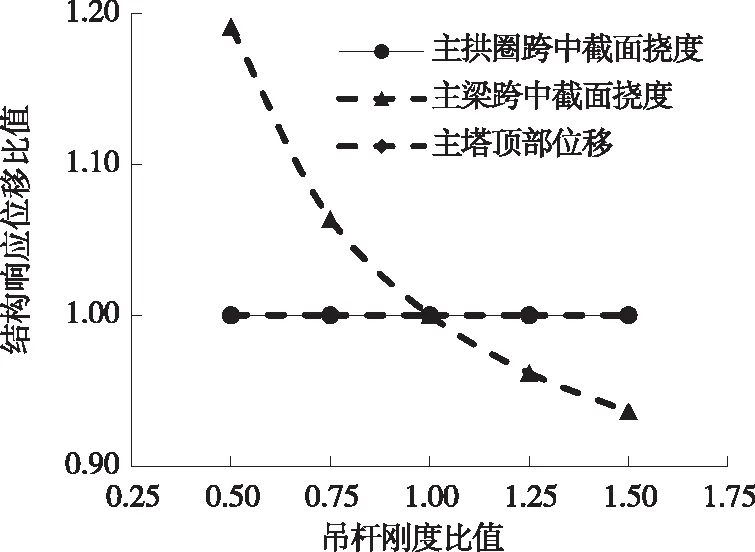
图10 吊杆刚度变化时结构响应位移比值

由图9、图10可知：吊杆刚度比值为0.5～1.5时，承载能力极限状态下，只有主梁和吊杆结构响应较明显，其他关键截面的内力和位移变化量均在1%以内。随着吊杆刚度的增加，跨中吊杆拉力逐渐增大，内力比值由0.98增加至1.01；主梁跨中弯矩逐渐减小，内力比值由1.17减少至0.93；主梁跨中截面挠度逐渐减小，位移比值由1.17减小至0.94。原因是拱式结构体系中，主梁在吊杆作用下可近似看作等间距连续梁结构，荷载作用下，吊杆刚度增加，吊杆力基本不变，吊杆弹性变形减小，主梁挠度减小。

由此可见，吊杆刚度参数在承载能力极限状态下对斜拉拱式体系整体结构响应及刚度变化的影响不大，对吊杆弹性变形、主梁挠度的影响较大。实际工程中吊杆需维持一定刚度，将吊杆自身弹性变形维持在较小值，以减少主梁挠度。

3.2 结构变化对体系受力的影响

大跨度桥梁体系中，结构恒载内力在桥梁体系运营阶段荷载中占比较大。考虑斜拉拱式体系设计中结构材料类型的选择对结构运营阶段内力、位移的影响，通过调整主梁结构和主拱圈结构容重进行分析，采用与3.1节相同关键截面和研究方法。

3.2.1 主梁容重对体系受力的影响

选择原设计方案中主梁结构容重的0.8、0.9、1.0、1.1、1.2分别建立有限元模型，获得各模型在承载能力极限状态下的响应。选取原设计体系中各关键截面位移和内力作为基本值，获得结构响应位移和内力与基本值的比值，结果见图11、图12。

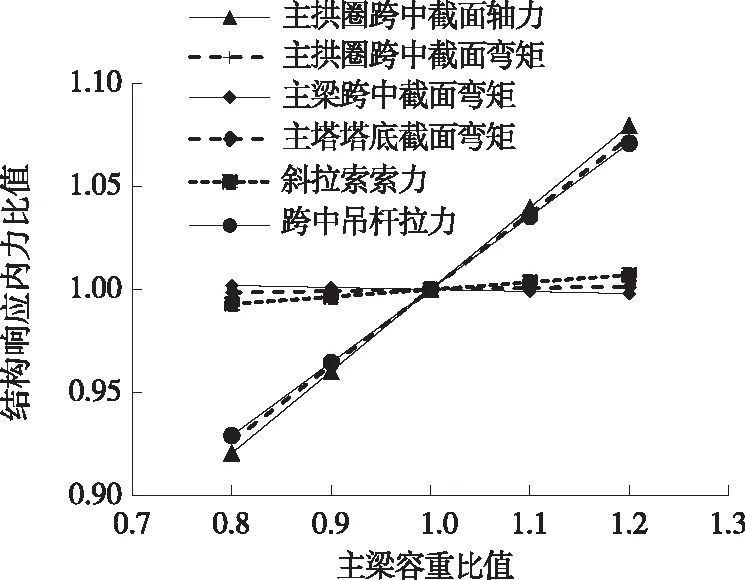
图11 主梁容重变化时结构响应内力比值

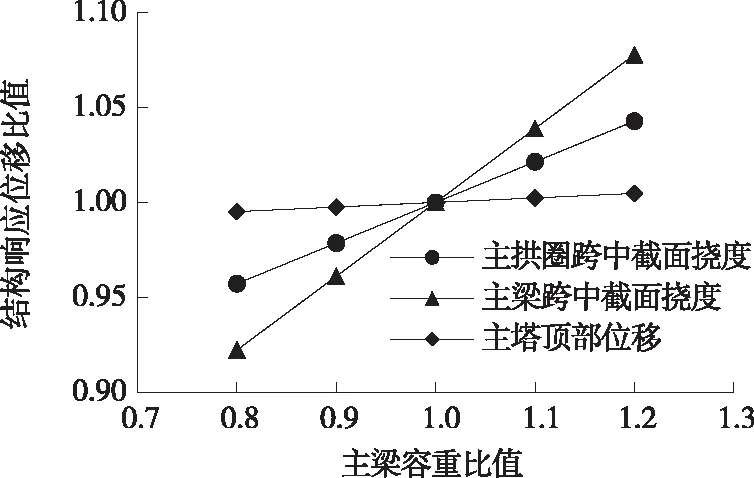
图12 主梁容重变化时结构响应位移比值

由图11、图12可知：主梁容重比值在0.8～1.2变化时，承载能力极限状态下，结构响应变化较明显，吊杆拉力、主拱圈跨中轴力、主拱圈跨中弯矩与主梁容重成正比例增加，近似于同一线性比例，内力比值由0.93增加至1.07。随着主梁容重的增加，主梁跨中挠度成比例增加，位移比值由0.92增加至1.08；主拱圈跨中挠度同样成比例增加，位移比值由0.96增加至1.04；其他关键截面的内力、位移变化量均在1%以内。

由此可见，主梁容重参数在承载能力极限状态下对斜拉拱式体系整体结构响应及刚度变化的影响较大，主梁容重变化荷载通过吊杆传输至主拱圈，较大程度影响主拱圈的受力，并引起斜拉索内力小幅变动，说明斜拉拱式体系中结构自重恒荷载主要由拱式结构承受，斜拉式结构承受少部分恒荷载。

3.2.2 主拱圈容重对体系受力的影响

采用3.2.1节相同的参数设置与研究方法，对主拱圈容重变化下体系受力进行分析，结果见图13、图14。

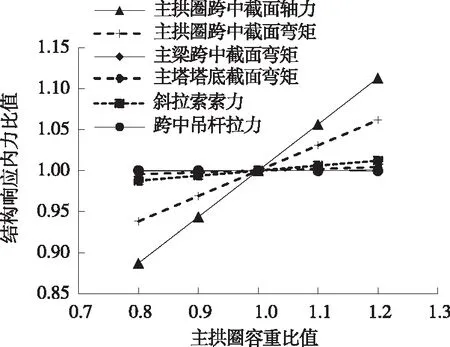
图13 主拱圈容重变化时结构响应内力比值

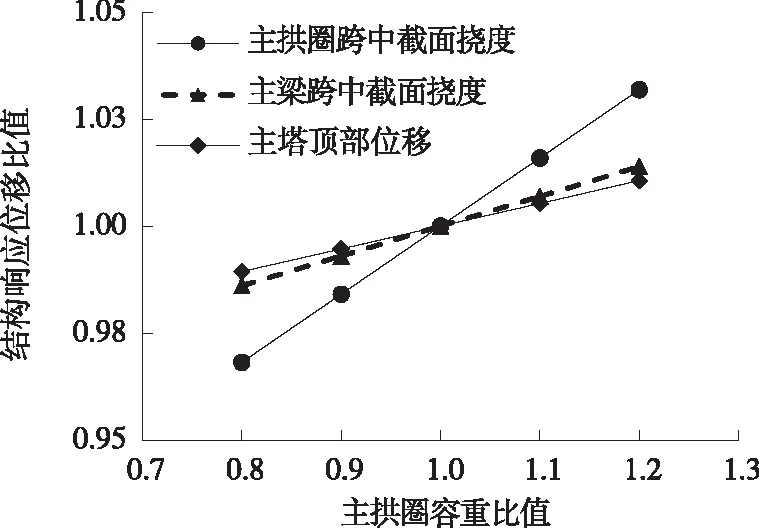
图14 主拱圈容重变化时结构响应位移比值

由图13、图14可知：主拱圈容重比值在0.8～1.2变化时，承载能力极限状态下，结构响应变化较明显。随着主拱圈容重的增加，主拱圈跨中轴力成线性比例增加，内力比值由0.89增加至1.11；主拱圈跨中弯矩成线性比例增加，内力比值由0.94增加至1.06；主拱圈跨中挠度同样成比例增加，位移比值由0.97增加至1.03，并引起主梁跨中挠度小幅增加；其他关键截面内力、位移变化量均在1%以内。

由此可见，主拱圈容重参数在承载能力极限状态下对斜拉拱式体系主拱圈自身受力的影响较大，并对其他结构产生小幅影响，说明斜拉拱式体系中结构自重恒荷载主要由拱式结构承受，斜拉式结构承受少部分恒荷载。

4 结论

以湘潭市莲城大桥为工程实例，通过MIDAS/Civil有限元软件建立模型，从材料性质、构件刚度等角度分析斜拉拱体系结构在承载能力极限状态下各参数变化对结构受力的影响，得出以下结论：1) 只改变拱肋刚度时，桥梁体系在相同荷载作用下的内力、位移响应明显，斜拉拱式体系整体刚度对拱肋刚度变化的响应较大，主拱圈挠度、主梁挠度与拱肋刚度成反比且变化明显，斜拉索索力与拱肋刚度成反比且变化较明显。2) 只改变斜拉索刚度时，斜拉索索力与斜拉索刚度成正比，主塔顶部位移与斜拉索刚度变化成反比，其他结构响应很小且关键截面内力、位移变化值均在1%以内。3) 分别只改变主梁、吊杆刚度时，桥梁体系主拱圈、斜拉索、主塔的内力和位移变化均很小，只对主梁内力和挠度产生较大影响，对结构整体刚度影响不大。主梁和吊杆需具有一定强度、刚度储备，以保证行车安全与行车舒适度。4) 分别只改变主梁容重、主拱圈容重时，桥梁体系在荷载作用下响应变化明显，结构自重在大跨度桥梁体系荷载中占比较大，设计中应减少结构自重，以增强活载承载能力。

综上，在桥梁运行阶段，拱肋刚度、主拱圈容重、主梁容重变化对斜拉拱式体系结构受力的影响较大，斜拉索刚度、吊杆刚度、主梁刚度变化对结构受力的影响较小。在桥梁运营阶段，主要以拱式结构受力为主，斜拉式结构受力为辅。因此，在斜拉拱式桥梁设计、运营、维护等环节以拱式结构为主。