螺旋桨激励水下艇体振动的试验及数值研究*

徐 野，熊 鹰，黄 政

(海军工程大学 舰船与海洋学院， 湖北 武汉 430033)

潜艇振动的激励源主要有艇内设备、螺旋桨和艇体表面湍流脉动等。近几十年来，各种主被动控制技术的应用使主机等机电设备的机械噪声得到了有效控制，潜艇在低速巡航时，艇体表面湍流脉动较弱，此时螺旋桨非定常负载通过轴系激励艇体的振动就凸显出来。国内外学者针对该问题开展了大量机理分析及控制措施的研究。Pan等[1]通过试验研究了水箱中螺旋桨激振力沿轴系到支撑板的传递特性，证明了推力轴承刚度对系统特性影响显著，试验中螺旋桨运转于静水中，其激振力的合理性还有待研究。Dylejko等[2]建立描述螺旋桨-轴系-艇体系统的传递矩阵，采用四端参数法研究了耦合系统的振动特性，认为建立桨轴系统动力模型时应考虑艇体的影响。Merz等[3]采用有限元和边界元方法对螺旋桨-轴系-艇体耦合系统的振动声辐射进行了研究。Caresta等[4]建立组合壳体及桨轴系统的运动方程，采用解析法计算了耦合系统在纵向及横向简谐激励力作用下的结构响应与声辐射，并探讨了结构参数的影响。曹贻鹏[5]采用空气中台架试验的方法研究了螺旋桨纵向激励力引起艇体振动的控制措施。吴仕昊[6]开展了吊放于水中的壳体在激振器作用下振动响应的试验研究。上述研究中的试验方式大多为空气中的台架试验，即使是文献[1]将螺旋桨置于水箱中，也无法考虑艇尾伴流场对螺旋桨的作用；计算方法多是采用单位简谐力作为激励源的谐响应分析，无法反应螺旋桨真实激励特性，适用于分析结构振动特性，但不利于振动响应的准确预报。

针对以上研究现状，本文在循环水槽中开展了艇尾伴流场中螺旋桨诱导艇尾脉动压力及螺旋桨激励水下艇体振动响应的测量试验，分析了脉动压力和振动响应的特性和变化规律；在验证了螺旋桨水动力性能和艇体伴流场计算准确性的基础上，采用计算流体动力学(Computational Fluid Dynamics, CFD)方法计算艇后螺旋桨的非定常负载；建立试验装置耦合系统整体有限元模型，采用模态叠加法计算其在螺旋桨激励作用下的强迫振动响应，并与试验值进行对比分析。

1 螺旋桨脉动压力及艇体振动响应测量试验

1.1 试验模型

试验对象的艇体为1 ∶1.25的SUBOFF主体+尾翼模型，如图1所示，主体采用钢制，整艇水密；尾翼采用聚四氟乙烯制作；螺旋桨模型为铝制，分为四叶桨INSEAN E779A和五叶桨DTMB 4382两种，由伺服电机驱动。模型主要参数为：总长L=3.485 m，直径D=0.406 m，螺旋桨直径d=0.180 m。试验场地为循环水槽，如图2所示。模型通过两个钢制剑杆吊装于水槽上方支架上，支架立柱直接安装于地面，不与水槽接触，可减小试验时水槽振动的干扰。

(a) 艇体(a) Hull

(b) E779A螺旋桨(b) E779A propeller (c) 4382螺旋桨(c) 4382 propeller图1 试验模型Fig.1 Test model

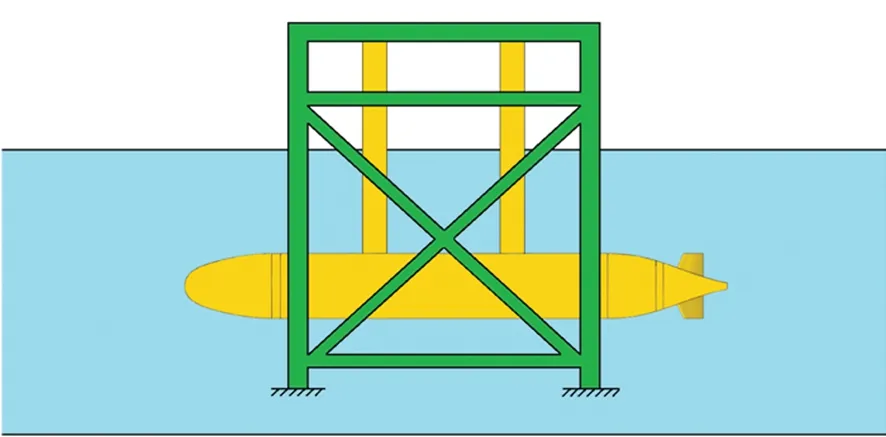
(a) 模型在循环水槽中的安装(a) Installation of the model in circulating water channel

(b) 水下艇体(b) Underwater hull图2 试验场地Fig.2 Test site

在螺旋桨前方的艇尾壳板底部布置4个压力传感器，用于测量螺旋桨诱导的艇尾脉动压力。其中1#、2#测点位于艇体正下方(尾翼后高伴流区)，3#、4#测点位于斜下方45°(尾翼间低伴流区)，1#、3#测点与桨盘面的轴向距离为0.58d，2#、4#测点与桨盘面的轴向距离为0.93d，具体布置情况如图3(a)所示。

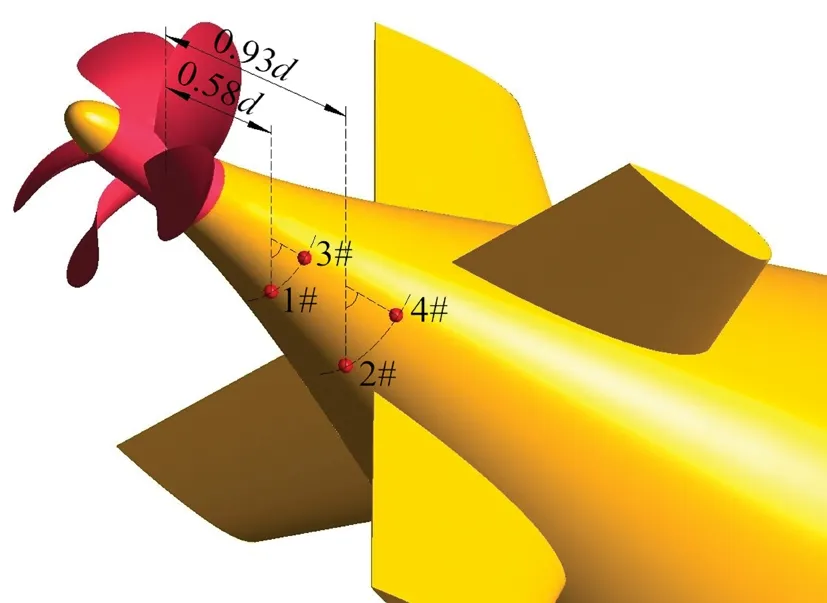
(a) 压力传感器(a) Pressure sensors

(b) 加速度传感器(b) Acceleration sensors图3 传感器布置Fig.3 Distribution of sensors

在艇体内部布置加速度传感器，在一些位置处还布置了若干不同方向的传感器，具体布置情况如图3(b)及表1所示(表中x为轴向，y为横向，z为垂向)。

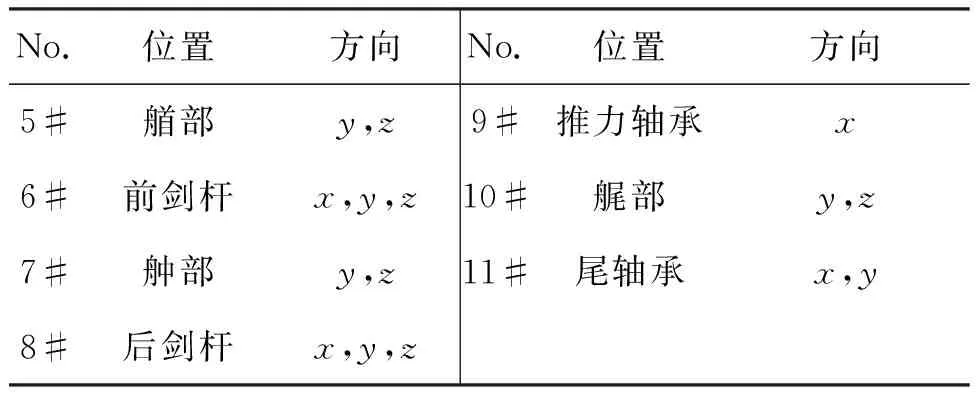
表1 加速度传感器位置及方向

1.2 试验内容

根据循环水槽和电机能力确定水槽的四个流速工况(流速V分别取1 m/s，1.5 m/s，2 m/s，2.5 m/s)及每个流速工况下螺旋桨的五个转速工况(转速n分别取8 r/s，10 r/s，12 r/s，14 r/s，16 r/s)，共20种工况。首先测量安装E779A桨时每种工况下的艇尾脉动压力和艇体振动加速度，然后换装4382桨，重复上述试验。将测得的脉动压力和振动加速度时域信号进行快速傅里叶变换(Fast Fourier Transform, FFT)，得到其频谱，用于进一步分析。

1.3 试验结果分析

取V=1 m/s、n=8 r/s为工况1，V=1.5 m/s、n=12 r/s为工况2，V=2 m/s、n=16 r/s为工况3，三种工况下螺旋桨进速系数相同，负载逐渐增大，选取以上三种工况进行分析。由于频谱中轴频、叶频和2阶叶频处峰值较为明显，且均在本文研究的低频范围内，因此选取以上三个频率处的幅值进行分析。分析时将幅值的单位换算为dB，参考压力取1×10-6Pa，参考加速度取1×10-6m/s2。脉动压力p测量结果如图4所示，图中每个测点处的三组数据从左至右分别为轴频、叶频和2阶叶频处幅值，可见脉动压力幅值在叶频处最大，且随螺旋桨负载增加而增大，随与螺旋桨距离增大而减小，E779A桨脉动压力在尾翼后的高伴流区(1#)幅值最大，4382桨则在尾翼之间的低伴流区(3#)幅值最大。

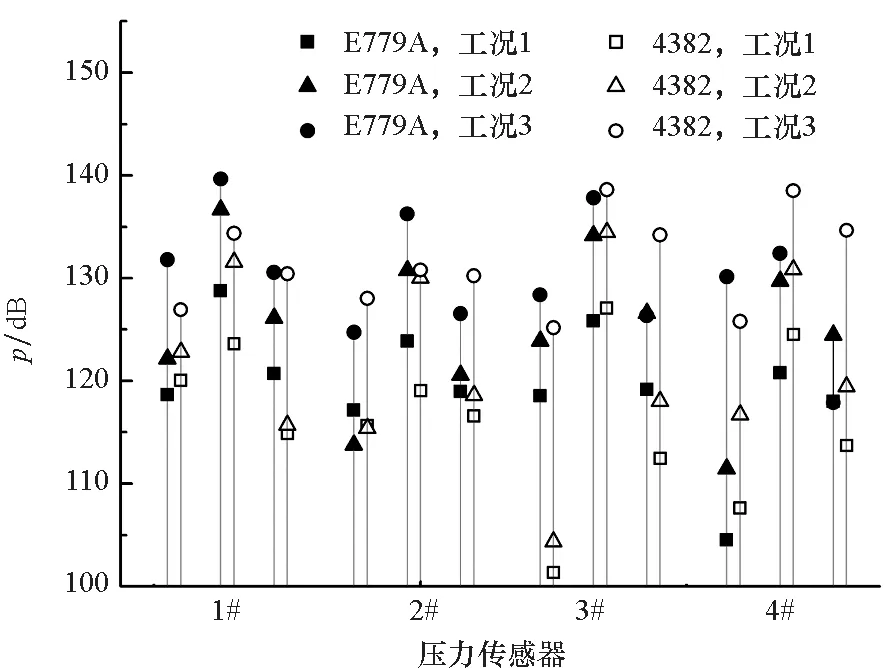
图4 脉动压力测量结果Fig.4 Measuring results of fluctuating pressure

E779A桨部分测点振动加速度La测量结果如图5所示，每个测点处的三组数据从左至右分别为轴频、叶频和2阶叶频处幅值。由图可见：大部分测点的振动响应随螺旋桨负载增加而增大；受模型本身的复杂振动特性以及电机和环境振动等干扰因素的影响，部分测点叶频处幅值比轴频、2阶叶频处更小，且少数测点的振动响应并未随螺旋桨负载增加而增大。

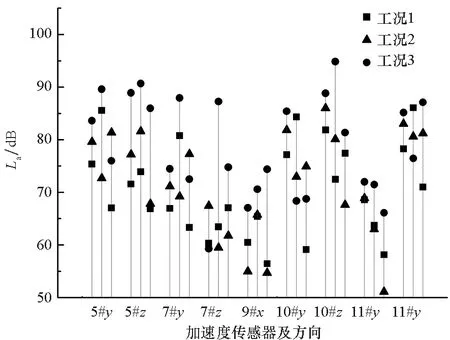
图5 振动加速度测量结果Fig.5 Measuring results of vibration acceleration

为研究螺旋桨激励特性与桨叶数的关系，同时测量了轴向及侧向(侧向包括横向和垂向)振动响应的测点(6#、8#、11#)进行分析。将两桨所有工况下的叶频处侧向加速度al与轴向加速度aa的比值进行对比，如图6所示。由图可见：大部分4382桨的al/aa大于E779A桨，说明其激励引起的侧向振动响应比E779A桨更强；大部分E779A桨的aa/al大于4382桨，说明其激励引起的轴向振动响应比4382桨更强；受电机及环境振动等干扰因素的影响，图中也有少部分数据并未呈现此规律。该现象与桨叶数和伴流场的关系有关，艇体尾翼产生四周期伴流场，当螺旋桨为四叶时，周向对称的四片桨叶同时进入高或低伴流区，各叶片的推力将同时达到高或低值，产生的轴向激振力较大，而侧向激振力因周向对称性可以相抵消而较小；当螺旋桨为五叶时，五片桨叶不能同时进入高或低伴流区，各叶片的推力高低值会因错位而补偿，产生的轴向激振力较小，而侧向激振力因周向非对称性无法相抵消而较大。

(a) al/aa

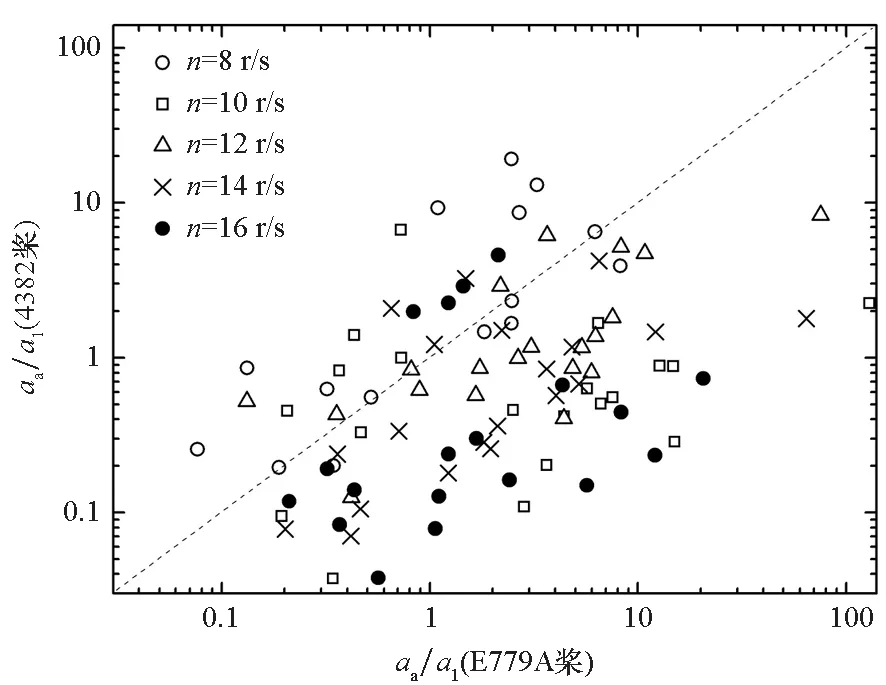
(b) aa/al图6 两桨al与aa比值的对比Fig.6 Comparison between the two propellers′ ratio ofal and aa

通过分析各测点横向及垂向振动响应频谱，能够看出特定谱峰频率处的振动响应与测点位置之间具有一定的关系。图7给出了工况2时艇体各测点在特定谱峰频率处的横向及垂向振动响应(E779A桨)，从图中可以看出，这些频率处的加速度幅值在艇首、中、尾部较大，在剑杆处较小，基本呈一阶弯曲振型。有限元计算得到的艇体一弯模态振型如图8所示，其中图8(a)～(b)为横向一弯模态，固有频率在80 Hz左右；图8(c)～(f)为垂向一弯模态，固有频率在70～75 Hz之间。由此可见，其范围与测量结果中的一阶弯曲振型频率较为一致，说明本文试验与计算结果吻合较好，都能够较为准确地反映出艇体振动特性。

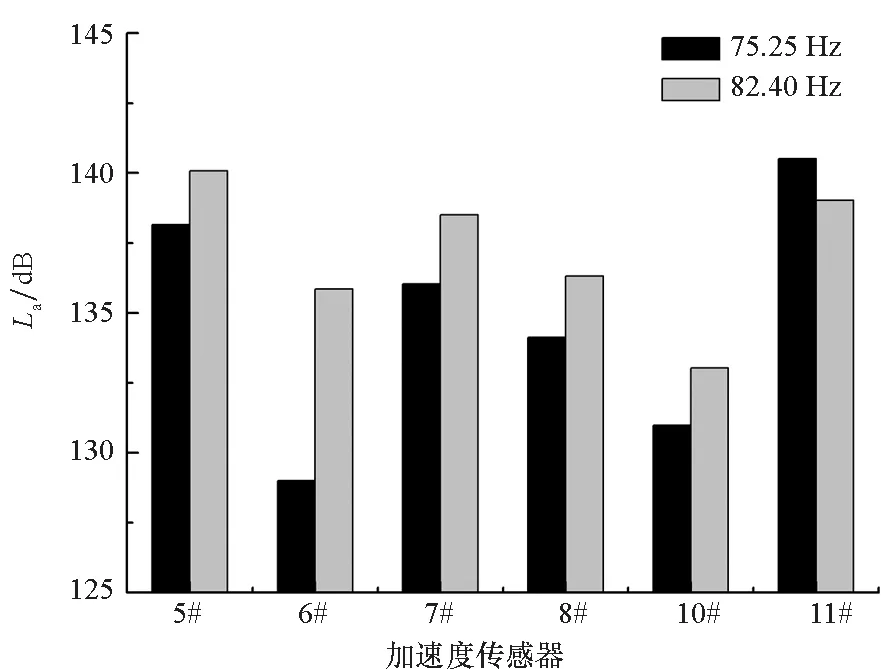
(a) 横向(a) Lateral

(b) 垂向(b) Vertical图7 艇体在特定谱峰频率处的振动加速度(E779A桨)Fig.7 Vibration acceleration of the hull at specific peak frequency(E779A propeller)

(a) 79.04 Hz

(b) 82.96 Hz

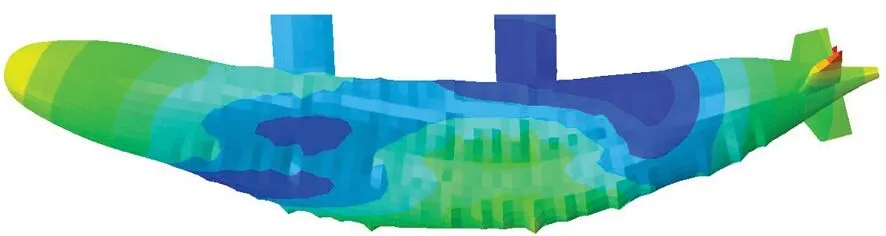
(c) 70.21 Hz

(d) 70.57 Hz

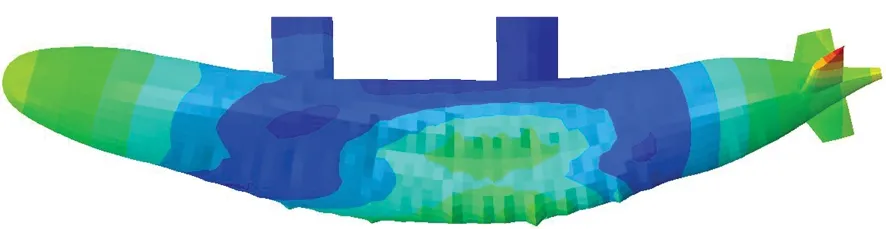
(e) 72.1 Hz

(f) 73.66 Hz图8 有限元计算得到的艇体一阶弯曲模态振型Fig.8 The 1st order bending mode of the hull calculated by finite element method

2 螺旋桨水动力性能及艇尾伴流场数值计算

2.1 计算模型与网格划分

采用CFD方法对螺旋桨敞水性能和艇尾伴流场进行数值计算，并与文献[7-9]中的试验结果对比，以验证本文计算方法的可靠性。计算模型的尺寸均与上述文献中相同。

黏性流体计算基于对N-S方程的求解，螺旋桨流场为湍流流场，湍流模拟采用RANS方法。为求解湍流方程，需选择合适的湍流模型以解决方程的封闭性问题，本文使用的湍流模型为剪切应力输运(Shear-Stress Transport，SST)k-ω模型[10]，该模型在近壁面区有较好的精度和算法稳定性。

螺旋桨敞水计算域采用结构化网格进行划分，分为静止域和旋转域，均为圆柱体。静止域前端位于桨盘面前2d处，设为速度入口；后端位于桨盘面后7d处，设为压力出口；圆柱面直径为10d，设为自由滑移壁面，网格数量约100万。旋转域直径为1.2d，前后端各距桨盘面0.25d，E779A和4382两桨网格数量分别约220万、250万，桨叶近壁面第一层网格厚度y+≤50。敞水计算域设置及网格划分如图9(a)～(c)所示。

艇尾伴流场计算对象为SUBOFF主体+围壳+尾翼模型，计算域为圆柱体，采用结构化网格进行划分，前端位于艇首前L处，后端位于艇尾后2L处，直径为2L，边界条件设置与前文静止域类似，网格数量约300万，艇体近壁面第一层网格厚度y+≤50。艇尾伴流场计算域设置及网格划分如图9(d)～(e)所示。

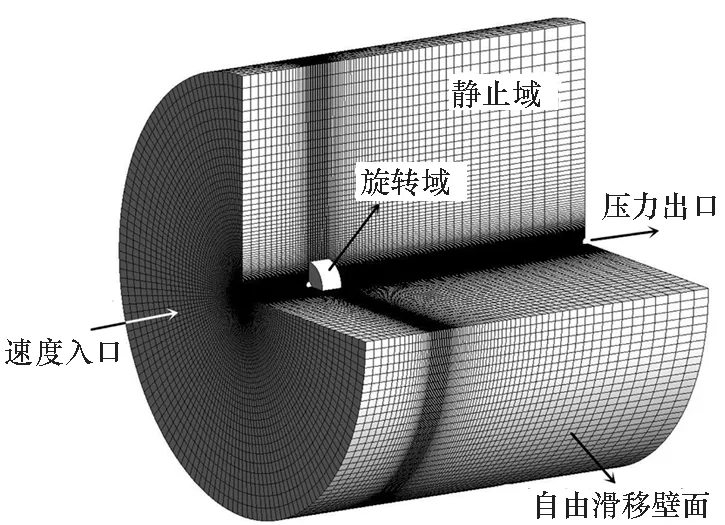
(a) 螺旋桨敞水计算域(a) Computational region of open water propeller

(b) E779A螺旋桨(b) E779A propeller (c) 4382螺旋桨(c) 4382 propeller

(d) SUBOFF伴流场计算域(d) Computational region of SUBOFF wake field

(e) SUBOFF艇体(e) SUBOFF hull图9 计算域设置及网格划分Fig.9 Computational region and grid

2.2 计算结果分析

使用成熟的CFD软件CFX进行数值计算。将螺旋桨转速设为10 r/s，采用多重参考系(Multiple Reference Frames, MRF)方法对一系列进速下的螺旋桨推力、转矩进行定常计算，结果如图10所示，其中J为进速系数，可见计算值与文献[7-8]试验值吻合较好，推力系数KT、转矩系数KQ的相对误差均小于5%。计算得到稳定的艇体伴流场后，取Re=1.2×107时，x/L=0.978，r/R=0.25处SUBOFF伴流的计算结果与文献[9]中风洞尾流场测量试验结果进行对比，如图11所示，其中u、v、w分别为轴向、径向、周向速度，U为来流速度，θ为周向角，可见计算值与试验值吻合较好。螺旋桨水动力性能和艇体伴流场的准确计算保证了螺旋桨在艇体伴流场中非定常负载计算的可靠性。

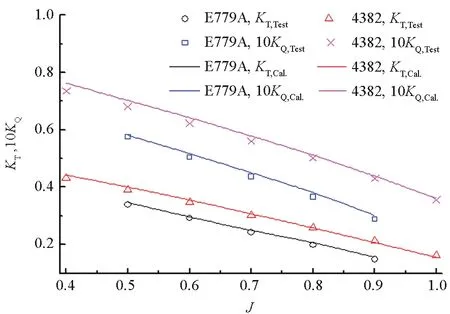
图10 螺旋桨敞水性能计算值与试验值的对比Fig.10 Comparison between numerical and experimental results of propeller open water performance

图11 SUBOFF伴流场计算值与试验值的对比Fig.11 Comparison between numerical and experimental results of SUBOFF wake field

3 艇后伴流场中螺旋桨激励艇体振动响应数值计算

3.1 螺旋桨非定常负载计算

本文计算方法的可靠性经过验证后，采用相同方法对工况2(V=1.5 m/s，n=12 r/s)下的艇后螺旋桨非定常负载进行计算。此时静止域横截面尺寸设为与循环水槽实际尺寸相同，其前端位于艇首前0.5L处，设为速度入口；后端位于艇尾后L处，设为压力出口；上端面设为对称面，其余边界均设为壁面，静止域网格数量约360万，艇体近壁面第一层网格厚度y+≤50。旋转域除修改桨毂形状外其余设置基本不变。计算域设置及网格划分如图12所示。

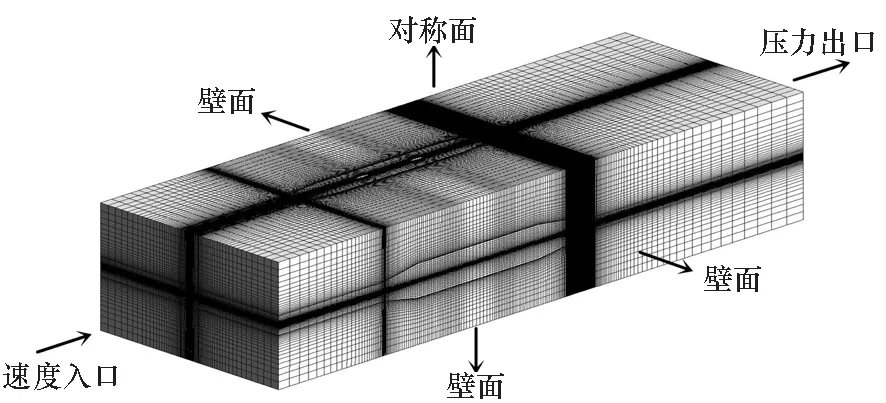
(a) 计算域(a) Computational region

(b) 艇体及螺旋桨(b) Hull and propeller图12 艇后螺旋桨计算域及网格划分Fig.12 Computational region and grid of behind hull propeller

采用滑移网格方法计算艇后螺旋桨的非定常负载，时间步长取螺旋桨旋转1(°)/步，结果收敛后，再计算1 s，将时域结果进行FFT后得到频域幅值。螺旋桨推力T计算结果如图13所示，图中以BPF表示叶频，以SF表示轴频，可明显看出两桨叶频及其谐频的各阶幅值，其中叶频幅值最大；由于螺旋桨处于四周期伴流场中，四叶桨E779A对称的两片桨叶同时进入高或低伴流区，其推力幅值比五叶桨4382更大；同时受四周期伴流场影响，4382桨在4的整数倍轴频处也可见较小的幅值。在240 Hz处，由于4382桨4阶叶频和20阶轴频两种作用的叠加，此处幅值略大。

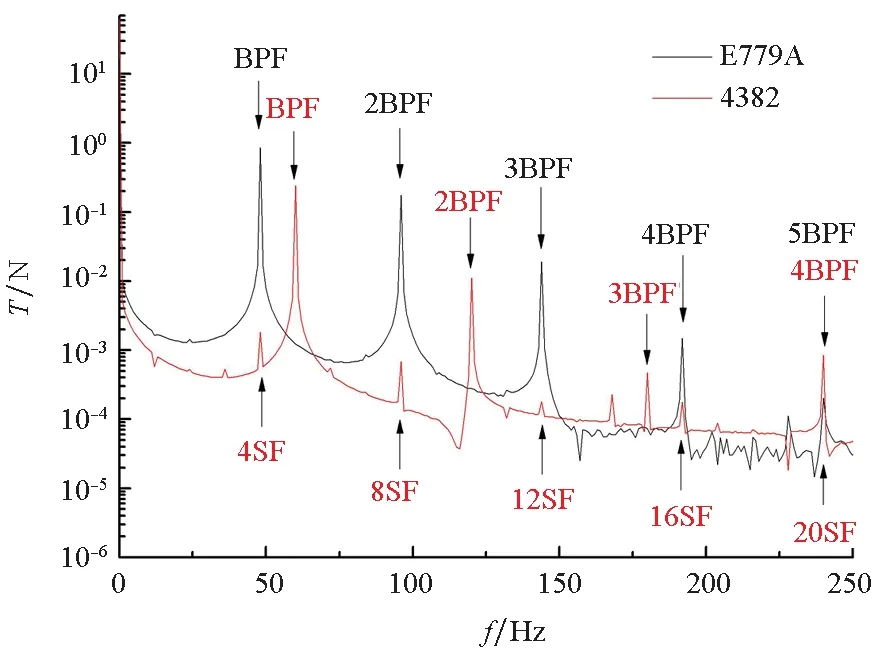
图13 螺旋桨推力计算结果Fig.13 Numerical results of propeller thrust

3.2 艇体振动响应计算

建立包括螺旋桨、轴系、艇体、支架的试验装置耦合系统整体有限元模型，采用添加附加流场的方式考虑水下艇体的流固耦合作用。其中轴系、骨架采用梁单元，单元数量约0.1万；艇体壳板、剑杆、支架采用壳单元，单元数量约1.2万；尾翼、艇内机械、附加流场采用实体单元，单元数量约3.7万；螺旋桨、压载等采用集中质量表示。有限元网格如图14所示。

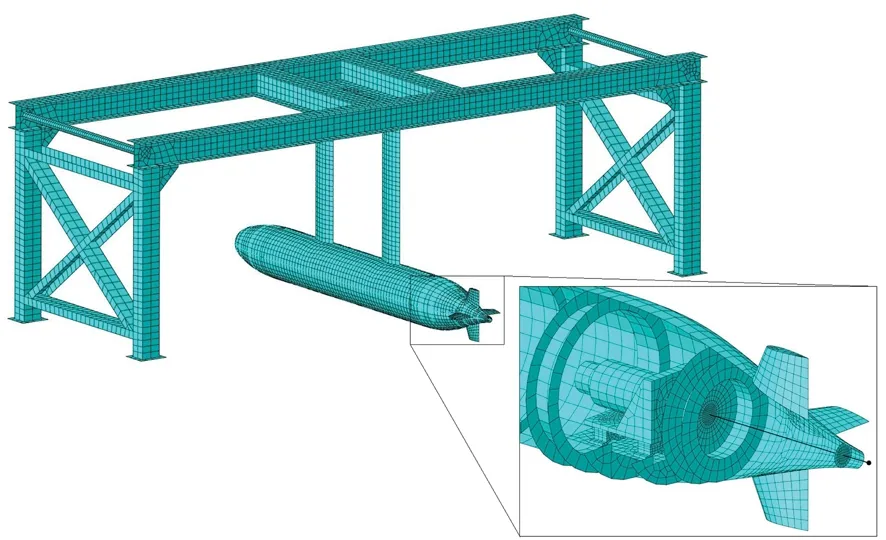
(a) 艇体及支架(a) Hull and support

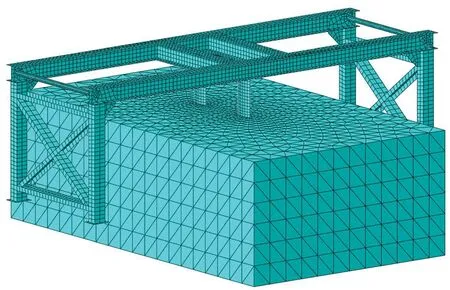
(b) 附加流场(b) Additional fluid field图14 有限元网格Fig.14 Finite element mesh

首先计算得到耦合系统模态并与试验数据进行对比，研究振动响应与测点位置之间的关系；然后采用模态叠加法[11]计算耦合系统在螺旋桨及电机等激励作用下的强迫振动响应。将计算得到的螺旋桨三个方向的非定常力Fpx、Fpy、Fpz及非定常转矩Mx、My、Mz加载于螺旋桨处；电机振动对试验结果的影响较大，在计算时不能将其忽略，因此将测量得到的电机三个方向的激振力Fmx、Fmy、Fmz加载于电机处，如图15所示。

图15 激振力的加载Fig.15 Loading of excitation force

3.3 计算结果分析

计算得到艇体振动响应后，取尾轴承处(11#)横向振动响应的计算值与试验值进行对比，如图16所示。由于电机激振力在各阶轴频处均有峰值，振动响应中也能观察到相应峰值，计算结果能够捕捉到试验结果频谱中的大部分峰值。两桨叶频(E779A桨为48 Hz，4382桨为60 Hz)处振动响应对比如图16(c)所示，可见计算值与试验值吻合较好，图中4382桨振动响应较E779A桨在48 Hz处较小而在60 Hz处较大，体现出两桨在叶频处的激励作用。艇体振动能量大部分集中于谱峰频率处，本文方法对此处振动响应的计算精度较高，说明该方法能够较为准确地预报艇尾伴流场中螺旋桨激励下艇体的振动响应，相比于采用单位简谐激励的谐响应分析方法更加接近水下艇体振动的真实情况。

(a) E779A螺旋桨(a) E779A propeller

(b) 4382螺旋桨(b) 4382 propeller

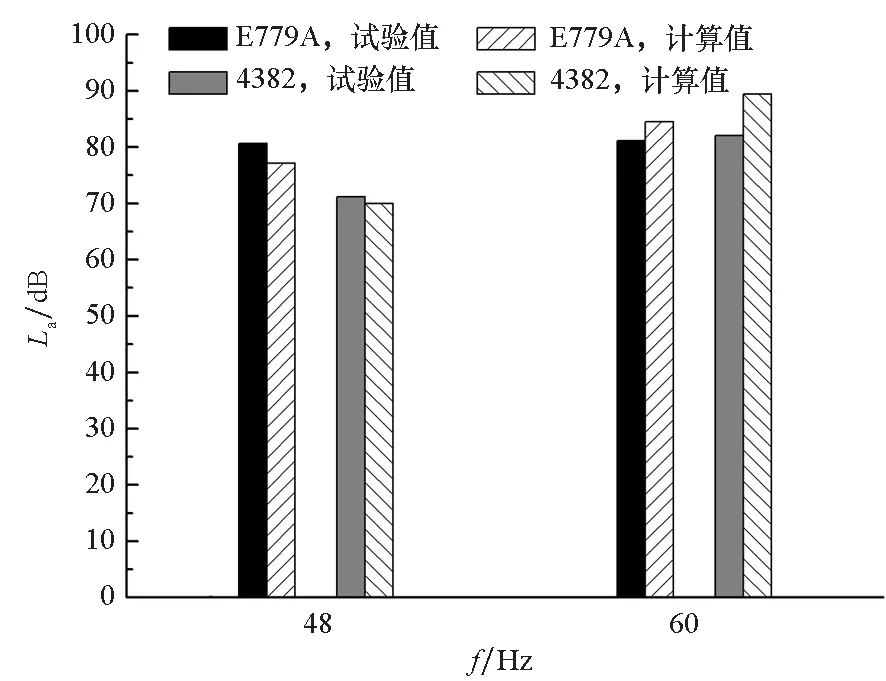
(c) 两桨叶频处振动响应对比(c) Comparison between vibration response of the two propellers at BPF图16 尾轴承处振动响应计算值与试验值的对比Fig.16 Comparison between numerical and experimental results of vibration response at stern bearing

4 结论

在循环水槽中开展了艇尾伴流场中螺旋桨诱导艇尾脉动压力及螺旋桨激励水下艇体振动响应的测量试验，综合采用CFD方法、有限元和模态叠加法建立了螺旋桨激励水下艇体振动响应的数值计算方法，并将计算与试验结果进行对比分析，得到如下结论：

1)螺旋桨诱导艇尾脉动压力幅值在叶频处最大，且随螺旋桨负载增加而增大，随与螺旋桨距离增大而减小，四叶桨脉动压力在尾翼后的高伴流区幅值较大，五叶桨则在尾翼之间的低伴流区幅值较大。

2)大部分测点的振动响应随螺旋桨负载增加而增大，受模型本身的复杂振动特性以及电机和环境振动等干扰因素的影响，部分测点叶频处幅值比轴频、2阶叶频处更小，且少数测点的振动响应并未随螺旋桨负载增加而增大。五叶桨激励引起的侧向振动较四叶桨有所增强，而轴向振动则有所减弱。

3)特定频率处的侧向振动响应在艇首、中、尾部较大，在剑杆处较小，呈一阶弯曲振型，且频率范围与有限元计算结果较为一致，试验与计算结果吻合较好，都能够较为准确地反映出艇体振动特性。

4)本文采用了更能反映螺旋桨真实激励特性的激励源，相比于采用单位简谐激励的谐响应分析方法更加接近水下艇体振动的真实情况，振动响应计算值与试验值吻合较好，尤其是能够捕捉到频谱中的大部分峰值，说明本文方法能够较为准确地预报艇尾伴流场中螺旋桨激励水下艇体的振动响应，可为相关研究提供参考，有助于实现水下艇体的减振降噪。