近地一次环月两次交会的载人登月任务规划*

2020-12-07贺波勇沈红新彭祺擘

国防科技大学学报 2020年6期

贺波勇，沈红新，彭祺擘

(1. 西安卫星测控中心宇航动力学国家重点实验室，陕西西安 710043；2. 载人航天总体研究论证中心，北京 100094)

载人登月是目前人类太空活动的巅峰之作，是世界高端科技和大国力量的展示平台，具有不凡的科学探索意义和重大的社会经济价值。Apollo任务是人类第一次成功载人登月任务，截至1972年12月，美国共有12名航天员登上月球，采集样品381.7 kg，完成科学实验约270项，产生了惠及后续至少50年的显著经济效益[1-2]。Apollo-17后，由于世界政治格局变化，载人登月进入静谧期。直到2004年，美国提出重返月球的“星座计划”，各航天大国也都加大了各自载人航天技术的研发力度。2010年，由于财政预算超支，美国重返月球计划被国会取消[3]。近年来，随着月球极地水冰及地下熔岩管道被发现[4-5]，美国鼓励商业力量进入该领域[6-7]，引起了世界其他国家关于地外空间及其他资源开发利用等问题的一次大讨论[8]。2016年，主题为“立足地月空间技术创新，推动载人航天持续发展”的第四届载人航天学术大会在哈尔滨工业大学召开，大会促进了我国载人登月基础技术的交流[9]。2017年，美国再次确立了重返月球计划[10]。

载人登月飞行模式设计是载人登月工程任务实施前期，总体研究和综合论证的重点工作。合理地设计飞行方案可以降低工程研发难度、缩短工期、提高任务可靠性，并节约经费。与Apollo任务近地一次发射的飞行模式相比，近地一次环月两次交会(RendezVous and Docking, RVD)的载人登月飞行模式具有相对较高的安全性和较小的运载火箭能力需求的优点，但其飞行阶段多、周期长、约束复杂，导致各阶段飞行窗口与轨道衔接匹配复杂的难题，给全任务规划带来了全新挑战。

假定任务基本需求与工程约束，设计了一种分层分解、正逆向结合的全任务标称飞行方案规划策略与轨道窗口衔接设计策略。

1 飞行模式特点与任务背景描述

1.1 飞行模式特点

按照地月转移过程中飞行器模块是否交会组装，交会所在轨道将现阶段比较成熟的载人登月飞行模式分为四类(Apollo经验：月面动力上升后均有一次环月交会对接[11])，分别是[12-19]：地面一次发射模式、低地球轨道(Low Earth Orbit, LEO)(或地球同步轨道)交会组装模式、环月低轨轨道(Low Lunar Orbit, LLO)(绕月大幅值逆行轨道幅值减小后为环月轨道[20])交会组装模式和LEO+LLO均交会组装模式。除了上述比较成熟的四类载人登月飞行模式外，近几年学者也研究了一些新型载人登月飞行模式，如地月L1点(拟)周期轨道交会组装模式[21-23]、地月L2点(拟)周期轨道交会组装模式[21,24]、周期重访轨道交会组装模式[25-27]和分步式人货分落模式(将月面人机联合模式归于此类)[28-30]。

新型载人登月飞行模式中：L1点和L2点是三体问题的鞍点，附近(拟)周期轨道不稳定，在真实空间引力环境中更易发散，需要长期测控；周期重访轨道目前面临的月心双曲轨道交会和地心大偏心率椭圆轨道交会问题燃料消耗较大，短期内难以实现；分步式人货分落模式需要解决月面定点着陆难题，目前还处于概念研究阶段。成熟的载人登月飞行模式中：地面一次发射模式发射阶段和地月转移过程均不能实现“人货分离”，风险最大；LEO交会组装模式地月转移过程不能实现“人货分离”，存在类似于Apollo-13任务的风险；LEO + LLO交会组装模式相比LLO交会组装模式对货运火箭能力的需求大幅度降低，是超重型运载火箭欠缺国家实施载人登月的首选模式。图 1 给出了近地一次环月两次交会的载人登月飞行过程，相比较于Apollo任务近地一次发射模式，该飞行模式阶段多、周期长、约束复杂，造成各阶段飞行窗口与轨道衔接匹配复杂的难题，给全任务规划带来了全新挑战。

1.2 任务背景描述

研究基于LEO + LLO交会对接组装的全任务规划方法，具有现实的工程价值。假定任务基本需求如下：

1)送3～4名航天员到月面进行科学考察；

2)任务实施年份约在2025年后；

3)月面科学考察活动时长约3 d；

4)月面着陆区域具备科学考察意义、资源利用价值及工程可实现性；

5)优先考虑在海南文昌基地发射，射向角可在90°～110°范围内调整；

6)优先考虑在四子王旗进行陆上中长航程着陆回收。

图1 近地一次环月两次交会组装飞行过程[12-13]Fig.1 Process of the manned lunar mission flight mode based on once LEO and twice LLO RVDs[12-13]

载人飞船与推进飞行器在LEO上交会组装后进行地月转移，近月制动后与先期停泊在LLO上的着陆器交会对接组装，航天员从载人飞船进入着陆器，与月面科学考察设备下降月面科考。完成月面考察后，着陆器上升级从月面上升，与载人飞船在LLO上进行第二次交会对接，航天员和月球样品转移至载人飞船，然后一起定点返回地球着陆场。以任务中三枚火箭地面发射、地月转移、交会对接、月面活动和月地返回等为主线，建立全任务飞行阶段剖面，如图2所示。

图2中：A代表月面着陆器，分为A1下降级、A2上升级；B代表推进飞行器；C代表载人飞船，C1为飞船服务舱，C2为飞船返回舱。关键窗口时刻均用T表示，上标A、B、C用以区别飞行器，下标0～13为任务主要窗口或轨道机动节点排序。着陆器近地停泊时长小于12 h，采用飞行时长约5 d的地月转移轨道。推进飞行器在着陆器月球捕获制动数天后发射入轨，近地停泊约3 d，调相配合载人飞船入轨相位，2 d之内完成近地交会对接，形成载人飞船与推进飞行器组合体，重新进行姿轨测控及必要准备后(用时约12 h)，采用绕月自由返回轨道进行地月转移，到达近月点后，24 h内完成三脉冲月球捕获制动，为环月第一次交会对接做准备，2 d之内完成环月第一次交会对接，航天员及月球科考设备向着陆器转移。任务设计月面动力下降前环月等待时长最多5 d，用来调整减小三脉冲月球捕获速度增量消耗。忽略月面动力下降和动力上升时长，月面科考3 d后，着陆器抛弃下降级，动力上升，2 d之内与载人飞船在环月轨道进行第二次共面交会对接，将航天员和月球样品转移至载人飞船。考虑月球公转和地球自转同向，预留25 h匹配着陆场经度，采用三脉冲完成月球逃逸加速制动，使载人飞船进入月地定点返回轨道，预定时间到达指定再入点，安全着陆地面。

由于该飞行模式全任务规模大、过程复杂、历时长，任务规划更注重在满足全任务所有约束条件的前提下，各阶段飞行窗口与轨道衔接匹配设计问题，给出科学合理的标称飞行过程。该飞行模式中决定全任务飞行窗口与轨道参数的关键窗口时刻、飞行任务和关键参数见表1。全任务规划问题是一个比较复杂的系统规划问题，目前并没有成熟的普适数学理论，也不能通过简单建立非线性规划模型直接优化计算，而需要根据经验，分析各个阶段约束条件的性质，制定一定的策略，分层逐步分解计算。

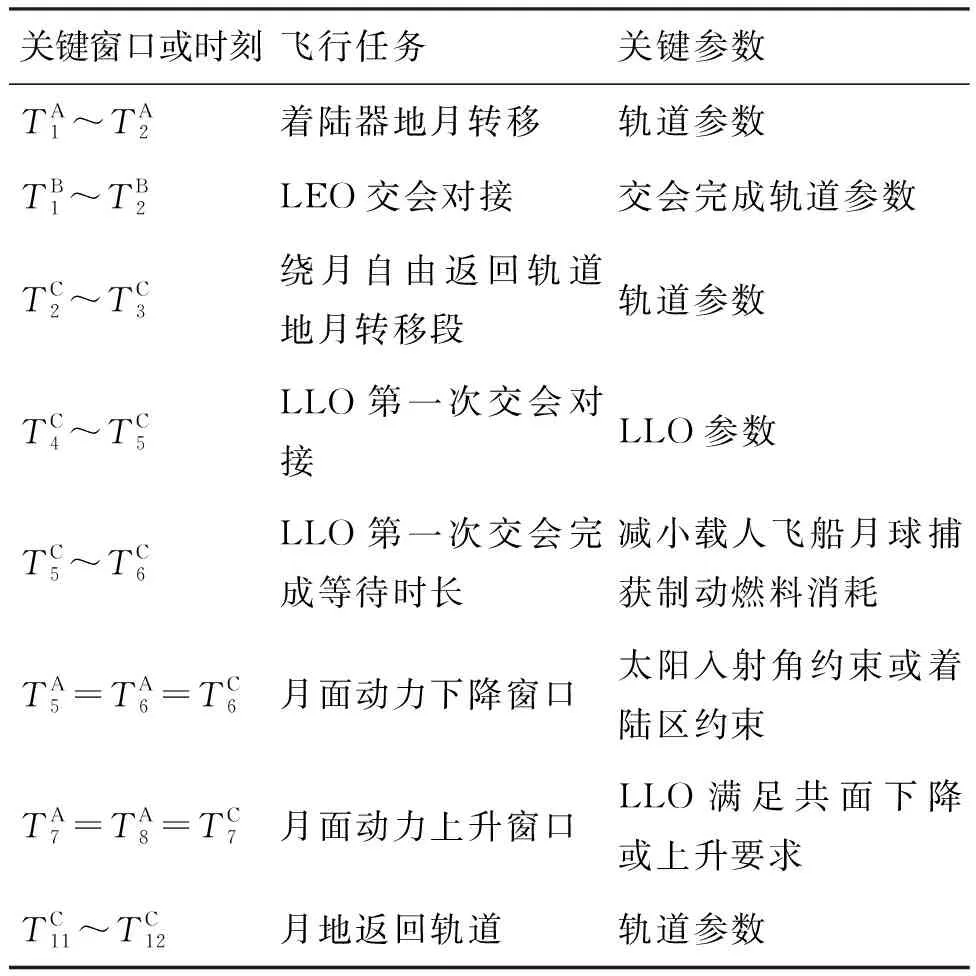
表1 全任务飞行阶段剖面中的关键参数

2 轨道动力学模型与主要工程约束

2.1 轨道动力学模型

载人登月轨道动力学模型中，最接近真实地月空间环境的是高精度轨道动力学模型。J2000地心坐标系中，采用微分方程描述的高精度轨道动力学模型如式(1)所示。

图2 全任务飞行阶段剖面Fig.2 Full mission flight phase profile

(1)

其中：r，v分别表示位置和速度矢量；μE表示地心引力常数；aN表示多体引力摄动加速度，地月系一般需要考虑太阳和月球中心天体摄动，相对位置采用JPL实验室公布的DE405/LE405星历插值计算；aNSE表示地球非球形摄动加速度，aNSL表示月球非球形摄动加速度；aSR表示太阳光压摄动加速度；aDrag表示地球大气摄动加速度，一般超过地球120 km高度即可忽略；aProp表示推进系统产生的加速度；O(aOther)表示木星摄动、相对论效应、潮汐及固体潮摄动等高阶小量，工程设计时一般予以忽略。

当飞行器接近月球时，为避免数值积分计算轨道时产生积分截断误差积累问题，宜采用J2000月心坐标系中的位置和速度矢量进行积分运算。此时，需要将J2000地心坐标系中的位置和速度矢量与J2000月心坐标系中的位置和速度矢量进行切换，切换方法一般是在飞行器穿越月球影响球时刻，通过JPL星历计算月地相对位置和速度矢量，并进行矢量相加。J2000月心坐标系中的轨道动力学模型与J2000地心坐标系中的形式类似，此处不赘述。

2.2 主要工程约束

载人登月任务需要考虑很多约束，一般而言，约束条件包括轨道运动学约束、光照约束和测控约束[31-37]。

2.2.1 轨道运动学约束

基于LEO+LLO交会对接的载人登月任务中，地月或月地转移轨道共有三种，分别为着陆器地月转移轨道、载人飞船地月转移轨道和月地返回轨道，除此之外，载人飞船与推进飞行器在LEO交会对接轨道和LLO轨道交会对接的环月目标轨道(Lunar Destination Orbit， LDO)都受到轨道运动学约束。按照时间先后顺序论述不同阶段约束条件。

1)着陆器地月转移轨道约束：着陆器地月转移飞行时长可在5 d左右选择，不严格限制，采用近地点切向单脉冲加速奔月和近月点切向单脉冲减速制动方式，瞄准LLO上第一次交会对接轨道LDO。

2)LEO交会约束：载人飞船和推进飞行器在LEO共面近圆轨道交会对接，且满足交会相位差约束。LEO交会轨道面倾角iE需与地面发射场纬度B0和射向角A0匹配，如式(2)所示。

cosiE=sinA0cosB0

(2)

3)载人飞船地月转移轨道约束：载人飞船采用绕月自由返回轨道进行地月转移(“星座计划”推荐载人地月转移方式[38])，与着陆器地月转移轨道不同的是，除采用近地切向单脉冲加速奔月外，近月端采用月心椭圆轨道三脉冲实现月球捕获，绕月自由返回轨道还需满足绕月自由返回地球再入点再入走廊约束。

4)月面共面下降和上升约束：由于月面动力下降和上升分别约消耗2 km/s速度增量，如果采取非共面动力下降和上升，速度增量将快速增长，工程中不可取。一般利用月球自转，设计LDO星下点轨迹经过目标探测区域，如图3所示。

图3 LDO共面下降和上升示意图Fig.3 Schematic of LDO coplanar descend and ascend

5)载人飞船月地返回轨道约束：考虑正常情况下返回我国四子王旗着陆场，直接再入大气减速后开伞着陆。由于四子王旗地理纬度约42°，宜采用跳跃式长航程再入弹道，要求月地返回出发时刻，月球位于赤纬南纬绝对值较大的时段。

2.2.2 光照约束

光照约束即为太阳入射角约束，一般包含两种约束：

1)月面动力下降时刻着陆点太阳入射角约束：月球自转和公转同周期，恒星月周期平均长度约为27.32 d，月昼和月夜各一半。月球没有大气，受太阳直晒，加之反照率仅7%左右，昼夜温差很大，白天太阳直射处高达127 ℃，夜晚最低可降至-183 ℃。受视觉和保温条件限制，月面科考均安排在月昼早晨。Apollo-11 任务动力下降过程中，受地形匹配导航敏感器反照率限制，太阳入射角βS∈[5°,14°][34]，如图4所示。

图4 着陆点太阳入射角约束示意图Fig.4 Schematic of the sun angle at landing site

2)地月或月地转移轨道太阳入射角约束：为了保证长时间转移飞行过程中飞行器电源补给，要求太阳帆板具有较好的受晒能力，即要求太阳入射角满足上下限约束。

βS∈[βSmin,βSmax]

(3)

地月或月地转移轨道大部分阶段贴近白道面，飞行器大部分时间处于巡航状态，帆板与体轴垂直且具有单轴自由度，考虑热电耦合的帆板在阳光入射角约大于36°时即可到达额定发电功率要求(βS∈[36°,90°])[35]。黄白夹角仅5°09′，所以，除非月食，绝大多数情况转移轨道太阳入射角都满足约束，只需避开月食即可，如图5所示。

图5 月食太阳入射角对航天器受晒示意图Fig.5 Schematic of the sun angle on the spacecraft when moon eclipse

2.2.3 测控约束

对于载人登月过程中，测控要满足任意时刻至少有一个地面站满足观测要求，在飞行过程中的关键制动点(包括地月转移加速、近月制动、月面动力下降或上升、月地返回出发等)前3 h、后4 h连续测控，精确定轨[36]。

3 全任务规划方法

3.1 总体规划步骤

全任务规划需要分层分解，逐步实施。本节分析各个阶段约束条件，制定总体规划策略。

所有约束中，月面动力下降时刻太阳入射角是由着陆区域在月固系中的经纬度决定，任务事先给定着陆点，动力下降时刻太阳入射角约束只能通过窗口调节。因此，月面动力下降窗口受到强约束。

主要约束条件中，载人飞船月地返回轨道约束是较强的约束。要想以较长航程直接再入大气返回我国四子王旗着陆场，月地返回出发时刻，月球赤纬值需为负值(南纬)绝对值较大处。对于载人飞船绕月自由返回轨道而言，可以采用月心椭圆轨道三脉冲捕获制动形成LLO。通过LLO第一次交会完成等待时长调节三脉冲捕获制动所需速度增量和从近地出发匹配LEO轨道倾角的日窗口。着陆器地月转移轨道虽然采用近地点切向加速出发，近月点切向减速制动，但制动后等待时长有很大调整空间，只需LLO在第一次交会对接时与载人飞船共面即可。

考虑上述因素，设计如下全任务规划策略：

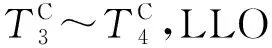
步骤2：计算目标着陆区域该时刻太阳入射角βS，判断是否满足约束条件βSmin≤βS≤βSmax：是，转入步骤3；否，返回步骤1。

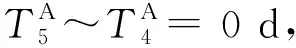
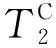
3.2 主要阶段轨道窗口计算方法

全任务规划按照上述7个步骤顺序反馈迭代。其中步骤1和步骤2只需通过简单的日-地-月空间几何方位即可判断，步骤3～6需要计算环月目标轨道LDO参数、载人飞船月地定点返回轨道参数、绕月自由返回轨道参数、着陆器地月转移轨道参数，本节着重介绍这4段轨道窗口规划方法，推进飞行器LEO交会调相研究比较成熟，本节不展开讨论。

3.2.1 环月目标轨道窗口计算方法

1)月固系中轨道面解析计算模型

一般而言，月面短期科考时长小于14 d(半个阴历月)，载人飞船采用绕月自由返回轨道或混合轨道进行地月转移，近月制动后形成月心逆行LDO，与着陆器交会对接。

月固系中倾角和升交点经度几何关系如图6所示，在球面三角△ABC中和△ADE中，分别存在如式(4)所示直角球面三角关系。

(4)

对于着陆点在月球北半球的情况而言，着陆时处于轨道降轨段，月固系中轨道倾角、升交点经度和近拱点角距分别为：

(5)

对于着陆点在月球南半球的情况而言，着陆时处于轨道升轨段。此时，月固系中倾角、升交点经度和近拱点角距分别为：

(6)

2)J2000月心系LDO计算方法

求解了着陆时刻月固系中的LDO倾角、升交点经度和近拱点角距之后，只需知道LDO高度hLDO，即可通过坐标转化计算此时J2000月心系中的轨道参数。月固系中修正轨道六根数近月距、偏心率和真近点角分别为：

(7)

将修正轨道六根数转化为位置及速度矢量(rL,vL)，通过J2000月心系和月固系转化关系(转化方法详见文献[37])，可以得到J2000月心系中该时刻LDO位置和速度矢量(rMJ2,vMJ2)。

3)月面动力下降窗口计算方法

月面动力下降窗口只需计算着陆区域太阳入射角是否满足约束。图7给出了虹湾(43° N, 31° W)2025年1月太阳入射角5°≤βS≤14°的窗口，可见，每个阴历月有两个窗口期，一个是月昼早晨，另一个是月昼黄昏(不可用)，每月一次的月面动力下降窗口可持续约24 h。

3.2.2 月地定点返回轨道窗口计算方法

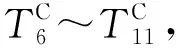
图6 月固系中倾角和升交点经度几何关系Fig.6 Geometry of the inclination and the ascending node longitude in the lunar-centric fixed coordination system

图7 2025年1月虹湾太阳入射角满足动力下降约束窗口Fig.7 Window satisfied solar elevation angle for lunar descend constraint in Jan.2025

(8)

式中，ωE,ωM分别为地球自转和月球公转角速度。

1)定点返回地球对月球赤纬要求

月地返回再入一般采用长航程(>6000 km)，再入角ϑ≈-6°，再入点到真空近地点地心扫角Δf满足：

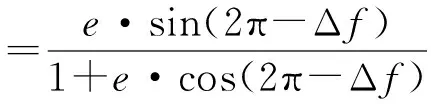
(9)

式中，e为月地返回轨道偏心率，一般约等于0.97。计算可得Δf= 12.2°。

(10)

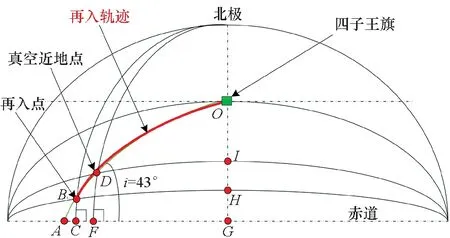
图8 月地返回再入真空近地点纬度估算示意图Fig.8 Schematic of the latitude estimation of the re-entry vacuum orbit from the moon

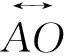
(11)

2)月面下降着陆与定点返回窗口耦合

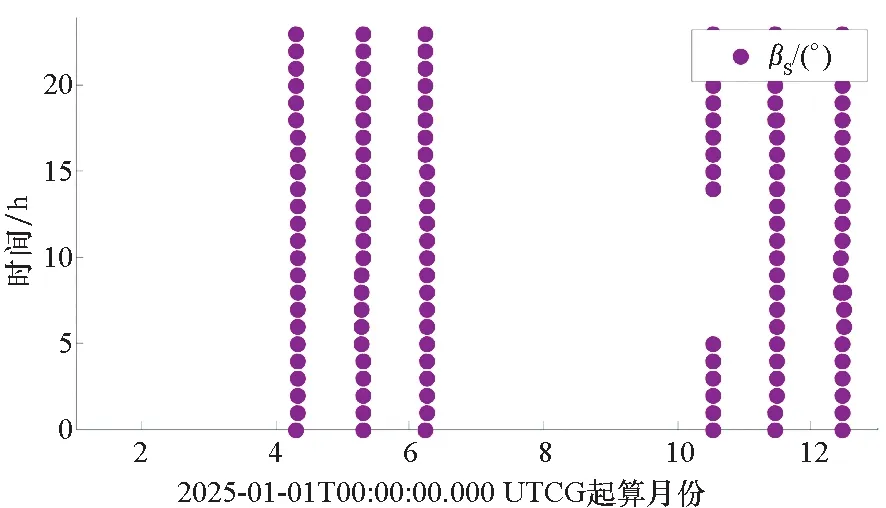
图9 2025年着陆虹湾且返回四子王旗的月面动力下降窗口Fig.9 Lunar descend window for landing Sinus Iridum and return Siziwang Banner in 2025

由图9可见，由于考虑返回地球中高纬四子王旗约束，虹湾月面动力下降窗口减小。2025年只有4、5、6、10、11和12共6个月存在为期约24 h窗口。再向后推算7.5 d，即可得到月地返回出发窗口区间。

3)月地返回轨道设计模型与求解方法

要想定点返回四子王旗着陆场，需在月地返回出发窗口区间前25 h范围内，匹配地固系中的着陆场经度。匹配着陆场经度时以15 (°)/h地球自转角速度为Newton迭代割线斜率，可迭代2～3次匹配目标经度值，轨道设计方法及算例验证如文献[40]所述，此处不再赘述。

值得讨论的是，由于LLO轨道面相对于惯性空间摄动运动范围有限，而月球在围绕地球以约13.2 (°)/d角速率公转，并非任意LLO任何时候都存在单脉冲月地返回轨道[32,39]。此时，需要三脉冲异面变轨，步骤如下：

步骤1：第1次脉冲先将应急返回飞船从LLO切向加速进入月心椭圆轨道，该椭圆轨道面与初始LLO轨道面法向一致。

步骤2：待飞行至椭圆轨道远月点，实施第二次变轨脉冲，调整椭圆轨道面法向与地月连线延长线方向垂直。

步骤3：飞行至与地月连线延长线的交线和近月点附近，寻找最优时机，实施第三次变轨脉冲，进入月地返回轨道。

图10给出了最差情况，即环月轨道面与月地连线垂直的三脉冲变轨示意图。

图10 LLO应急返回变轨方案示意图Fig.10 Schematic of emergency return plan form LLO

LLO应急返回变轨可以采用月心二体轨道解析计算初值，再进一步计算高精度轨道动力学模型解。已有研究表明：对于LLO高约111 km、月心椭圆周期为24～48 h的情况而言，最差情况下，三脉冲变轨速度增量值小于1450 m/s，椭圆周期为48 h相比24 h情况能减少约134 m/s的速度增量[17,41]。

3.2.3 绕月自由返回轨道窗口计算方法

载人登月任务初期，为了保证航天员在地月转移段任务中止后仍能安全返回地球，载人飞船通常采用绕月自由返回轨道进行地月转移。技术成熟度增加后可以考虑采用混合轨道方式进行地月转移。NASA注重工程实施安全性，推荐采用绕月自由返回轨道，并在近月点减速制动成月心大椭圆轨道，在远月点附近轨道面交线处变轨，再次飞抵近月点轨道机动圆化的三脉冲变轨方式[38]。

1)绕月自由返回轨道设计模型与求解方法

绕月自由返回轨道在近地出发、近月点和返回地球再入时刻都存在较为苛刻的约束，约束参数类型不同，敏感度不同，且分布在三个可变时间点。绕月自由返回轨道再入点参数与近地出发参数敏感度高，对轨道动力学模型精度要求较高，导致直接采用非线性优化算法和高精度模型的求解策略往往不能计算出结果。作者在文献[42]中提出了采用近月点参数作为设计变量，采用逆向和正向高精度数值积分相结合的方式设计绕月自由返回轨道。并在后续研究中，消除了逆向数值积分插值近地点截断误差导致再次正向积分误差放大的问题[43]，此外不再赘述。

2)自适应LEO相位精确窗口计算方法

(12)

3)月心大椭圆三脉冲变轨方案

NASA充分吸收Apollo-13任务的经验和教训，特别强调绕月自由返回轨道对于航天员安全保障的必要性，提出通过月心椭圆轨道扩展月面可达域的方案[41]，如图11所示。

图11 二体模型估算月心椭圆变轨轨道示意图Fig.11 Schematic of the estimation of lunar ellipse orbit using two-body model

在绕月自由返回轨道近月点施加一次切向月球捕获减速制动脉冲，形成月心椭圆轨道，在远月点附近轨道面交线处实施第二次脉冲，待再次飞回近月点时，第三次脉冲将轨道圆化。这种方案需要增加月心大椭圆过渡轨道飞行时长和一定速度增量等额外的代价，但是保留了地月转移段的绕月自由返回安全特性，变轨后也具有良好的飞行稳定性。易知，椭圆轨道远月点高度与周期正相关，远月点速度与周期反相关，远月点附近第二次脉冲尽可能小与椭圆变轨额外飞行时长尽可能短二者是对立而不可兼得的。

椭圆轨道变轨方案设计变量多，直接采用高精度模型优化计算存在初值猜测的困难。宜先利用月心二体轨道模型估算初值，再用高精度模型优化修正求解。月心二体模型解析计算公式和高精度模型计算方法详见文献[17]，研究表明，第一次和第三次速度增量和不变(该算例恒为947.648 m/s)，即从一个固定的绕月自由返回轨道近月点变轨形成环月目标圆轨道的总能量消耗不变。

调整轨道面的第二次速度增量脉冲大小受两轨道异面差和变轨处真近点角值影响很大，如图12所示，异面差越大，速度增量脉冲越大，变轨处真近点角距离近月点越近，速度增量脉冲越大。椭圆变轨方案理论上可以实现全月面到达，需携带约2550 m/s速度增量对应的燃料用于月球捕获制动。而实际工程中，飞行器很难携带这么多速度增量对应的燃料用于近月制动。因此，应采用环月等待时长和尽可能将绕月自由返回轨道近月段轨道面设计的接近LDO轨道面等其他方式，调整交线变轨处的真近点角，用来减小第二次速度脉冲，减小全月面到达需要的额外代价，这也是NASA推荐的策略[41]。

图12 第二次调整轨道面速度脉冲与交线和异面差关系Fig.12 The second velocity impulse amplitude versus intersecting-line and the angle of two different orbital planes

3.2.4 着陆器地月转移轨道窗口计算方法

仿真算例表明：高精度轨道动力学模型中，LDO轨道摄动演化范围较大且不规律，采用高精度轨道动力学模型数值积分计算是十分必要的。一个朔望月存在两个着陆器月窗口区间，窗口区间大小与LEO出发倾角正相关。

4 算例

仍以2025年实施载人登月，探测目的地为虹湾，从海南文昌发射场发射，并返回四子王旗为假想场景为例，任务背景描述详见1.2节。

4.1 环月目标轨道

表2 月面动力下降时刻环月目标轨道六根数

表2中：κ、e、i、Ω、ω、f分别为修正轨道六根数中的近心距、偏心率、倾角、升交点赤经、近拱点角距、真近点角。下标“MJ2”表示月心J2000坐标系。

4.2 月地定点返回轨道

月地定点返回时刻为月面动力下降时刻2025-04-08T18:35:00.000 UTCG之后7.5 d：2025-04-16T17:35:00.000 UTCG。此时，月球赤纬值为-26.4° S，小于-14.2°，符合定点返回四子王旗条件。按照3.2.2节方法可以得到如表3 所示的月心J2000坐标系中的月地返回轨道修正轨道六根数。

表3 月地返回轨道入轨时刻月心J2000坐标系中的六根数Tab.3 Orbital parameters of trans-earth injection in moon-centered J2000 coordination

该条轨道约于2025-04-19T6:43:41.250 UTCG抵达真空近地点，真空近地点在地球固连坐标系中经度为79.39° E，地心J2000坐标系中的修正轨道六根数如表4所示。

表4 月地返回轨道真空近地点时刻地心J2000坐标系中的六根数Tab.4 Orbital parameters of trans-earth orbit at the moment of vacuum perigee in earth-centered J2000 coordination

表4中，下标“EJ2”表示地心J2000坐标系。采用三脉冲方案实施月地定点返回的速度增量分别为0.562 73 km/s, 0.191 39 km/s和0.359 35 km/s。

4.3 绕月自由返回轨道

为尽可能提升运载能力，使海南文昌发射的射向角接近90°，且考虑降低近地一次交会的燃料消耗，采用3.2.3节自适应LEO相位调整的载人飞船绕月自由返回轨道设计方法，计算得到一条2025-03-29T4:14:18.750 UTCG近地出发的绕月自由返回轨道，近地出发时刻地心J2000坐标系中的轨道六根数如表5所示。

表5 绕月自由返回轨道近地出发时刻地心J2000坐标系中的六根数Tab.5 Orbital parameters of circumlunar free-return orbit at the moment of trans-lunar injection in earth-centered J2000 coordination

该条轨道约于2025-03-31T18:35:00.000 UTCG抵达200 km高近月点，近月点时刻月心J2000坐标系中的修正轨道六根数如表6所示。

表6 绕月自由返回轨道近月点时刻月心J2000坐标系中的六根数Tab.6 Orbital parameters of circumlunar free-return orbit at the moment of perilune in moon-centered J2000 coordination

到达近月点后，采用周期为24 h的月心大椭圆调整轨道面与LDO轨道面一致，三脉冲变轨的速度增量分别为0.365 02 km/s、0.266 90 km/s 和0.560 64 km/s。

推进飞行器的发射窗口和轨道参数需根据载人飞船近地加速进入绕月自由返回轨道之前的LEO轨道参数和LEO交会对接相位要求逆向推算。我国已经掌握LEO交会对接技术，相关文献较多，此处不再赘述相关方法和轨道窗口参数。

4.4 着陆器地月转移轨道

表7 着陆器地月转移轨道近地出发时刻地心J2000坐标系中的六根数Tab.7 Orbital parameters of lunar lander trans-lunar orbit at the moment of trans-lunar injection in earth-centered J2000 coordination