驱动控制对太阳帆板驱动系统动力学特性的影响*
2020-12-07朱仕尧雷勇军
朱仕尧,郭 欣,雷勇军
(国防科技大学 空天科学学院, 湖南 长沙 410073)
太阳帆板驱动系统(Solar Array Drive System,SADS)一般由太阳帆板及其驱动装置(Solar Array Drive Assembly,SADA)组成。SADA内部激扰因素会产生附加的扰动力矩,造成太阳帆板运动不平稳,引起结构振动扰动;而太阳帆板结构振动又会反过来影响太阳帆板运行平稳性和扰动力矩幅值,降低高精度航天器指向精度、成像质量或通信频率等性能指标[1]。开展驱动系统扰振特性分析和有效抑制扰动力矩都需要首先准确分析驱动系统动力学特性。
太阳帆板驱动系统包括太阳帆板转动引入的刚柔耦合效应、SADA闭环伺服驱动控制以及SADA和太阳帆板之间的动力耦合等多种耦合因素[2],这些因素会对其系统动力学特性产生影响,增加系统动力学特性的分析难度。在早期研究中,SADA往往被考虑为刚性体,不考虑SADA与太阳帆板的动力耦合,驱动系统动力学特性仅表现为太阳帆板结构模态特征,可以采用集中参数模型[3]、模态坐标模型[4]、悬臂欧拉梁模型[5]、固支-自由-自由-自由边界的基尔霍夫板模型[6]以及有限元模型[7-8]等表征。随着SADA研究不断深入,研究人员开始关注SADA自身的刚度和阻尼特征。这些研究往往采用刚性附件代替柔性太阳帆板。Low[9]、Yang[10]和Middleton[11]等主要研究了由步进电机内部机电耦合引起的电磁刚度和阻尼特性。Cabilic[12]和Wood[13]等证明了SADA内部滑环结构的摩擦会引入额外的阻尼。Lu等[14]研究了驱动系统减速装置齿轮咬合间隙对扰动特性的影响。近些年,研究人员开始探索在系统动力学分析中综合考虑SADA和太阳帆板的结构特性。Sattar[15]、Chen[16]和Li[17]等研究了带有柔性负载的驱动系统扰动特性问题,其中采用集中参数模型模拟柔性负载,对步进电机进行线性化处理,获得其等效电磁刚度。Zhu等[2, 18]在理想控制假设和稳态运动假设下,推导了SADA的等效刚度和等效阻尼,并提出了一种驱动系统动特性分析方法。以上研究往往将驱动系统限定在低转速模式,对驱动控制进行理想化假设,以简化问题难度。Zhou等[19]利用输入成形器对驱动控制指令进行预处理,以减少快速驱动后的残余振动扰动,但未对快速捕获或转角归零等高转速模式下的驱动系统动力学特性进行讨论。
针对上述问题,本文摒弃驱动控制理想化假设,重点推导考虑驱动控制因素的SADA等效力学特性参数,构建SADS动力学特性等效分析模型,通过仿真和试验验证模型正确性,并研究不同转速条件下驱动控制增益对SADS动力学特性的影响规律,对工程型号改进设计、扰振特性分析以及振动控制研究具有重要参考价值。
1 驱动系统动力学特性等效分析模型
1.1 驱动系统动力学模型
SADS坐标系定义如图1所示,其中OXYZ为惯性坐标系,oxyz为太阳帆板随体坐标系。航天器本体的质量和频率特性均明显大于SADS,可将其简化为固定约束的刚性体。根据SADS工作流程(如图2所示)可知,系统动力学模型可由驱动控制、驱动装置和太阳帆板等子模型组成。
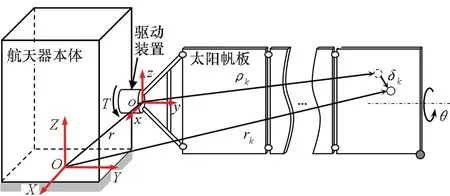
图1 太阳帆板驱动系统组成Fig.1 System composition of SADS

图2 驱动系统工作流程Fig.2 Typical workflow of SADS
1.1.1 驱动控制
SADA一般采用步进电机作为驱动执行部件。由于其每个输入脉冲所对应的转角是定值,因此脉冲信号的频率与驱动速度成正比,可以通过开环控制实现驱动速度控制。为避免步进驱动引起较大幅度的力矩波动,电流细分器对步进电机参考电流进行微步阶跃形式的三角函数细分。如图3所示,随着电流细分数的增加,参考电流细分阶跃幅度逐渐减小。

图3 电流细分数对参考电流的影响Fig.3 Relationship between current fraction and reference current

(1)

在参考电流细分基础上,电流控制器通过步进电机绕组电流与参考电流之间的偏差反馈调整驱动电压(以下简称为电流环),使绕组电流跟随参考电流变化,从而保证驱动速度与实际转速趋于一致。根据电机的电压平衡方程可以得到实际电流ij的表达式:

(2)
式中:R和L分别为绕组阻抗和电感系数;Km为电磁力矩系数;ωm和θm分别为电机转子转速和转角。设定电流控制器采用PI控制律调整驱动电压uj:
(3)
式中:KP和KI分别为比例和积分控制增益。
1.1.2 驱动装置
含有减速装置的SADA力矩平衡方程[20]为:
(4)
式中:Tl为驱动力矩;Jm为转子转动惯量;ρg为减速装置传递效率;电磁力矩Te和摩擦力矩Tf分别表示为
(5)
Tf=σ0ωl-[Tc+(Ts-Tc)e-(ωl/ωs)]sgn(ωl)
(6)
其中:σ0为黏性摩擦系数;Tc和Ts分别为库伦摩擦力矩和最大静摩擦力矩;ωs为临界Strebeck转速。
含有减速装置的SADA运动方程为:
(7)
其中:ωl和θl分别为太阳帆板转速和转角。
1.1.3 太阳帆板
根据虚功原理,当不考虑高阶小量时,可以建立考虑太阳帆板刚体转动、柔性振动以及两者耦合的柔性太阳帆板结构动力学模型[2]:
(8)
式中:Hl为模态角动量矩阵H第一行向量;Jl为转动惯性矩阵J第一个对角元;η为太阳帆板模态坐标;D和Λ分别为模态阻尼矩阵和特征值矩阵。 将式(4)代入式(8),并结合式(1)~(3)得SADS动力学模型。
1.2 步进电机绕组电流表达式
稳态太阳帆板驱动系统运动具有如下特点:
(9)
此时电机实际转速和平均驱动速度之间的误差很小,即电机转动的运动规律满足如下关系:
(10)
将式(10)代入式(2),可近似得到:

(11)
再将式(11)代入式(3),可整理得到:
(12)
如图4所示,充分细分后的稳态绕组电流可以近似为与参考电流同频振荡、但幅值和相位不同的三角函数,因此第j相绕组电流为:

(13)
式中,γc和φc分别为绕组电流相对参考电流的幅值比和延迟相位,其与参数P和Q的关系式为:
(14)

图4 绕组电流和参考电流时间历程曲线Fig.4 Time history curves of winding and reference current

(15)
式(15)只有在正弦项和余弦项系数同时为0的情况下才能成立,可以列写代数方程组并求解得到:
(16)
进一步将式(16)代入式(14),可以得到驱动控制增益、绕组特性以及转速等参数与绕组电流幅值和相位的关系。
1.3 驱动装置等效力学特性
以两相混合式步进电机为例,将式(13)代入式(5)可得电磁力矩为:
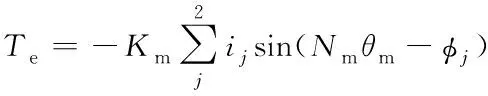
(17)
因此式(4)中的驱动力矩可整理为:
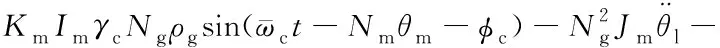
σ0ωl-[Tc+(Ts-Tc)e-(ωl/ωs)]sgn(ωl)
(18)
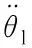

(19)
式中:转速ωl系数的绝对值σ0为考虑驱动控制后的SADA等效阻尼;转角θl系数的绝对值K′d为SADA等效刚度,具体表达式为
(20)
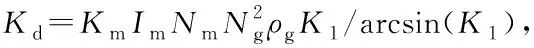
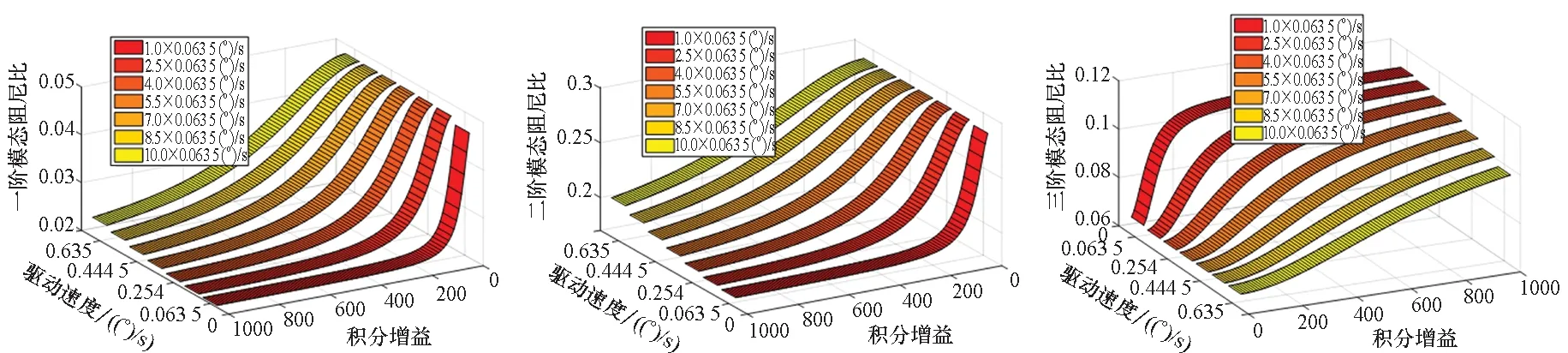
由于0 将式(19)代入式(8),可得SADS动力学特性等效分析模型: (21) 图5 驱动系统动力学特性等效模型Fig.5 Dynamic-characteristics equivalent model of SADS 图6给出了分别采用参数辨识方法、考虑驱动控制的等效模型和基于理想驱动控制假设的等效模型得到的驱动系统一阶扭转模态固有频率和模态阻尼比随驱动速度的变化曲线。由图可知:①在驱动速度趋近0.063 5 (°)/s且控制增益为700时,三者计算得到的驱动系统动力学特性参数吻合较好。②随着驱动速度逐渐增大,参数辨识结果与考虑驱动控制的等效模型所得动特性变化规律一致,固有频率均随驱动速度增大而逐渐减小,模态阻尼比随驱动速度增大而逐渐增大;且控制增益越小,模态参数变化幅度越大。然而,基于理想驱动控制假设的等效模型所得系统模态参数均不随转速和控制增益变化,其与参数辨识的相对误差随驱动速度增大和控制增益减小而增大。③在驱动速度趋近0.635 (°)/s时,参数辨识和考虑驱动控制的等效模型所得固有频率的相对误差为-2.32%,阻尼比相对误差为-1.88%;而基于理想驱动控制假设的等效模型所得固有频率和阻尼比与参数辨识方法的相对误差分别可达4.71%和-57.11%。以上分析说明:基于理想驱动控制假设的等效模型在驱动速度增大后出现应用局限性,而考虑驱动控制的等效模型可以适应驱动速度和控制增益的变化。 (a) 一阶固有频率(a) 1st natural frequency (b) 一阶模态阻尼比(b) 1st model damping ratio图6 系统动力学特性参数与转速关系曲线Fig.6 Relationship curve between dynamic characteristic of SADS and rotational speed 试验件为驱动装置和太阳帆板模拟件构成的驱动系统(如图7所示)。驱动装置为低轨直接型SADA;太阳帆板由两块铝合金薄板组成,用于模拟太阳帆板在驱动方向的质量和刚度特征,满足转动惯量等效和结构基频等效原则。为抵消模拟件对驱动装置轴承的压力,在驱动系统的转动轴线方向配备龙门吊和吊装组件以卸载重力。 测试系统由Kistler六自由度测力平台、Polytec激光测振仪、信号放大器、数据采集器、计算机和SADA外置驱动器以及动力学试验分析软件等组成,如图7所示。测力平台通过螺栓与SADA转接工装固定连接,用于测量驱动系统的扰动力矩分量。激光测振仪测量驱动装置转速,激光测点布置在太阳帆板刚性转接工装上。测量结果分别经过信号放大器和测振仪后置端进行处理,并通过数据采集器传递给计算机。SADA外置驱动器用于产生脉冲信号控制太阳帆板转动。 图7 驱动系统扰动特性测试系统Fig.7 Disturbance-characteristics test system of SADS 在驱动系统匀速驱动后增加停止指令,记录驱动系统在停止段的残余振动响应,并对该段自由振动数据(如图8所示)进行傅里叶变换得到频谱分布特征。扰动力矩衰减曲线表现为单频震荡特点,幅度随时间增加而逐渐减小;在频谱曲线低频段存在明显峰值,所对应频率0.656 Hz即为驱动系统基频。参考试验状态建立太阳帆板模拟件与驱动装置等效刚度和阻尼模型。根据文献[2]参数确定驱动装置等效刚度为680 N·m/rad,等效阻尼为60 N·m·s/rad。通过模态分析得到其在固定支撑边界条件下的动力学特性,其中一阶模态振型同为围绕驱动方向的一阶扭转振动,对应基频为0.610 Hz,与试验结果相对误差为-7.01%。 (a) 时间历程(a) Time history (b) 频谱分布(b) Frequency spectrum图8 驱动系统停止段扰动力矩Fig.8 Disturbance torque in the stop phase of SADS 图9给出了不同驱动速度下SADS各阶扭转模态固有频率随比例增益的变化曲线。由图可知:①驱动速度大于4倍0.063 5 (°)/s时,前两阶固有频率先随比例增益显著增大而后逐渐趋于稳定,最小的固有频率取值位于最小的比例增益位置并随驱动速度减小而增大,且固有频率趋于平稳时的临界比例增益取值随模态阶数增大而增大;第三阶固有频率在所见区域内始终与比例增益成正相关关系,未出现稳定阶段。②驱动速度小于4倍0.063 5 (°)/s时,固有频率均随比例增益先微幅减小而后趋于稳定。以上分析说明:驱动系统固有频率仅在驱动速度较大且比例增益较小时才会变化;当比例增益增大后,固有频率不随驱动速度和比例增益而改变。 图10给出了不同驱动速度下SADS各阶扭转模态阻尼比随比例增益的变化曲线。由图可知:①驱动速度大于4倍0.063 5 (°)/s时,前两阶模态阻尼比随比例增益增大而显著减小,随后保持稳定;在驱动速度小于4倍0.063 5 (°)/s时,模态阻尼比先小幅增大而后趋于平稳,且稳定值按模态阶次顺序逐渐增大。②第三阶模态阻尼比的变化趋势与前两阶相反,其在驱动速度大于4倍0.063 5 (°)/s时,随比例增益增大而增大;在驱动速度小于4倍0.063 5 (°)/s时,第三阶模态阻尼比先小幅减小然后趋于稳定;模态阻尼比最小值对应比例增益的最小值,并随驱动速度增大而减小。以上分析说明:各阶模态阻尼比的变化趋势并不相同,但是都会在比例增益较小且驱动速度较大时发生变化,在比例增益大于特定值后趋于稳定。 图11为不同驱动速度下SADS各阶扭转模态固有频率随积分增益的变化曲线。由图可知:①当驱动速度较小时,固有频率逐渐增大并最终达到稳定取值;②随着驱动速度的增大,固有频率增大速度在逐渐减小,特别是当驱动速度大于5.5倍0.063 5 (°)/s后,固有频率在所研究范围内始终随积分增益增大,而未趋于稳定。 图12为不同驱动速度下SADS各阶扭转模态阻尼比随积分增益的变化曲线。由图可知:①前两阶模态阻尼比均随积分增益增大而减小,且减小速率随驱动速度增大而逐渐减小;同阶模态阻尼比最大值均对应积分增益最小值;驱动速度增大会使模态阻尼比最小值不断增大。②第三阶模态阻尼比随着积分增益的增大而增大;在最小驱动速度工况下,其首先随积分增益显著增大,然后趋于稳定;随驱动速度增大,模态阻尼比增大速率不断减小;在最大驱动速度工况下,模态阻尼比随积分增益增大而平稳增加。 (a) 第一阶固有频率(a) 1st natural frequency (b) 第二阶固有频率(b) 2nd natural frequency (c) 第三阶固有频率(c) 3rd natural frequency图9 比例控制增益对系统固有频率的影响Fig.9 Relationship between the proportional gain and the natural frequency of SADS (a) 第一阶模态阻尼比(a) 1st model damping ratio (b) 第二阶模态阻尼比(b) 2nd model damping ratio (c) 第三阶模态阻尼比(c) 3rd model damping ratio图10 比例控制增益对系统模态阻尼的影响Fig.10 Relationship between the proportional gain and the model damping ratio of SADS (a) 第一阶模态阻尼比(a) 1st model damping ratio (b) 第二阶模态阻尼比(b) 2nd model damping ratio (c) 第三阶模态阻尼比(c) 3rd model damping ratio图12 积分控制增益对系统模态阻尼的影响Fig.12 Relationship between the integral gain and the model damping ratio of SADS 针对驱动控制对太阳帆板驱动系统动力学特性影响问题,构建了动力学特性等效分析模型,开展了模型正确性验证,分析了控制增益和驱动速度对驱动系统动力学特性的影响规律。主要结论如下: 1)驱动控制不会改变驱动装置的等效阻尼,但会使驱动装置等效刚度减弱,且减弱程度与驱动速度成正比,与控制增益成反比。 2)所构建的等效分析模型能够在不同驱动速度和控制增益情况下准确预示驱动系统动力学特性,分析结果与试验数据误差小于10%。 3)驱动系统固有频率与控制增益成正相关关系,与驱动速度成负相关关系。 本研究扩展了驱动系统动力学特性分析理论的工程适用范围,可以为具体工程型号的扰振特性分析以及振动控制方案设计提供理论支撑和技术参考。1.4 动力学特性等效分析模型
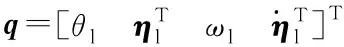

2 动力学特性分析模型正确性验证
2.1 仿真验证


2.2 试验验证



3 驱动控制对系统动力学特性的影响分析
3.1 驱动速度和比例增益对系统动力学特性影响
3.2 驱动速度和积分增益对系统动力学特性影响


4 结论
