自修复型微胶囊内部微裂纹损伤特性的仿真分析
2020-12-07李伯男
夏 宇,李伯男,李 熙,蔚 超,刘 洋
(1.重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044;2.国网江苏省电力公司电力科学研究院,江苏 南京 211103)
0 引言
电力工业是关系国计民生的基础产业,随着我国经济持续快速的发展,人民生活水平不断提高,对稳定可靠安全的电力需求日益增大。电缆由于其受外界因素影响小、可靠性高、对市容环境影响小、相对更安全等优点得到了越来越广泛的应用。但电缆成本高、难于检修、接头施工工艺复杂等特点又限制着电缆的应用。并且电缆深埋地下,一旦发生事故,就会造成人力物力等的较大损失。电缆聚乙烯绝缘层在长期运行条件下会产生微孔和微裂纹等损伤,并且电缆接头处绝缘外表面也会因操作产生划痕损伤。在电场的持续作用下,固体绝缘材料内部的微裂纹处会出现微放电现象,长期的微放电会引发电树枝的生长,导致绝缘材料击穿,从而引发事故。
现有的检测技术难以发现电缆绝缘层中的微孔和微裂纹等微小缺陷,并且在电缆绝缘层损伤后除停电更换外无其他可靠的修复方式,这无疑给电力供应带来了巨大的损失。
自修复概念为解决电缆绝缘层微损伤提供了一个很好的思路。通过微胶囊自修复体系制备的自修复型聚乙烯材料能够在损伤发生的初期自行对这些损伤进行修复,在理论上能很好地解决电缆绝缘层出现微孔和微裂纹这一问题,具有重要的研究价值。
微胶囊应具有足够的强度,在电缆受到外力作用时能保持完好,不会出现破裂;此外,当电缆产生微裂纹等微小损伤时,微胶囊能及时破裂,释放出愈合剂,防止裂纹扩展并起到一定的修复作用。因此,了解和掌握微胶囊材料在电缆中的受力情况、微裂纹扩展情况以及微胶囊在微裂纹作用下的破裂行为是非常关键的。
1 聚乙烯/微胶囊复合材料模型参数获取
1.1 聚乙烯/微胶囊复合材料制备
微米级双环戊二烯(DCPD)微胶囊采用较为复杂的原位聚合“两步法”来制备。这种制备方法总体反应过程稳定,并且可控性高,产物形态和性能也较优越。
在成功制备得到性能较优的微米级DCPD微胶囊后,模仿原始聚乙烯薄膜制备方法,通过熔融共混的方法制备LDPE/微胶囊复合材料薄膜样品。
1.2 复合材料的观测与模型几何参数的选择
使用扫描电子显微镜对微胶囊进行测试,结果如图1所示。

图1 微胶囊形态SEM图Fig.1 SEM images of microcapsule morphology
从图1(a)可以看出,微胶囊整体形态呈现较好的球状,并且分散性良好,粒径分布较为集中;进一步放大后,从图1(b)可以看出,多数微胶囊呈现良好的球形,且无明显损伤或裂纹,同时表面有细微凸起,微胶囊粒径大多维持在100 μm左右。图1(c)是破损的微胶囊壁材结构,可以看出壁材外表面粗糙,内表面光滑,有研究指出粗糙的外表面有利于微胶囊与基体的界面啮合作用,而光滑的内表面更有利于囊芯内修复剂的流出过程,增强浸润效果,提升修复速度。由图1(d)可以观察出其壁厚约为3 μm,因此,之后的仿真环节设定微胶囊的壁材厚度为3 μm。
为了更精确地定量分析微胶囊的粒径大小,使用激光粒度仪对微胶囊的粒径分布进行了分析,结果如图2所示。从图2可以看出,微胶囊粒径分布较窄,集中于100 μm两侧,两侧有小峰存在,证明尺寸过大和过小微胶囊占总体的比例很小,可看出自修复型复合绝缘材料的整体性能主要受100 μm尺寸的微胶囊影响。
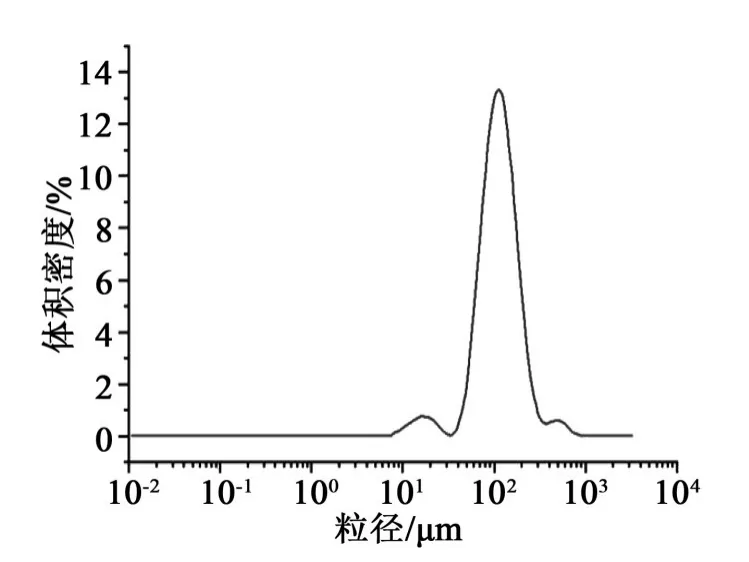
图2 微胶囊粒径分布图Fig.2 Particle size distribution of microcapsules
综上所述,制得的微胶囊以及微胶囊复合材料满足材料要求。同时,根据材料的观测,选定微胶囊直径为100 μm,微胶囊壁厚为3 μm。
1.3 复合材料模型力学性能参数选择
本研究中材料LDPE的力学性能参数在制备前后几乎没有变化,所建模型选定其杨氏模量为0.172 GPa,泊松比为0.439。
2 复合材料中微胶囊的受力分析
2.1 微胶囊受力模型
微胶囊是通过聚合物膜材料将液体或气体包裹起来制造成的微小颗粒,本研究中的微胶囊囊壁材料是脲醛树脂,囊芯材料为液体愈合剂。
2.1.1 微胶囊模型的几何参数
本研究采用的微胶囊模型与实际试验中制备的模型形状大小均相同,其内部是囊芯,囊芯物质可视为不可压缩的液体,并且在作用过程中微胶囊体积保持不变。
2.1.2 微胶囊模型的材料属性
建立的微胶囊受力模型有以下几个设定:①微胶囊囊壁厚度均匀,即各处厚度均相同,不承受弯矩的作用;②微胶囊囊壁材料为弹性材料且是各向同性的线性材料;③复合材料基质各处弹性模量相同,泊松比相同。在以上假定条件下,微胶囊和LDPE基质的参数可以采用杨氏模量和泊松比进行描述。本研究设置囊壁材料的弹性模量为2 GPa,泊松比为0.3。
因为囊芯是液体材料,在受力过程及微胶囊的破裂过程中造成的影响非常小,并且在软件仿真中液体材料的设定非常困难,所以在模拟微胶囊受力仿真时微胶囊采用仅有外层微胶囊壳的模型。
2.1.3 微胶囊的受力分析
微胶囊在电缆绝缘层材料中,主要受到LDPE压缩和拉伸力的作用,这两种形式的作用力都可以通过作用于包裹微胶囊的LDPE来传导给微胶囊。由于受力的复杂性难以通过理论分析求得,本研究采用的仿真方法是提供给微胶囊一定的形变位移,当形变位移与材料属性都确定时,材料的应力分布与所受载荷大小均能通过仿真得到。微胶囊除受载荷作用,也会受到约束作用,即微胶囊与LDPE间会存在一定的力干扰微胶囊的移动,故本研究在微胶囊周围施加一定的力的作用对其进行约束。
2.1.4 微胶囊仿真模型的建立
微胶囊仿真模型是由微胶囊囊壁壁和包裹微胶囊的LDPE基体组成,为计算方便,将基体设置为挖去微胶囊部分的圆柱体,如图3所示。
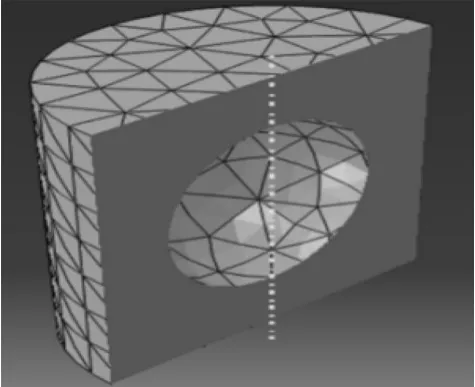
图3 LDPE基体仿真模型Fig.3 Simulation model of LDPE matrix
2.2 微胶囊的仿真结果分析
在本研究的有限元仿真分析中,默认的应力是Mises应力标量结果。仿真的目的是找到最大的受力区域与受力数值。同时,力在不同方向、不同区域的不同形式也是需要密切关注的,因此也分析了不同方向上微胶囊壁的应力变化,其中受拉为正,受压为负。
2.2.1 拉伸作用下微胶囊的应力分布状况
仿真时设置材料的形变位移分别为0.08 μm和0.04 μm(相对于基体长度,形变率分别为0.1%和0.05%),微胶囊壁拉伸等效应力分布云图如图4所示。由图4可知,当形变位移增大时,微胶囊壁各处的位移和应力也随之增大,对于微胶囊囊壁材料来说,其最大屈服力出现在中间区域。从图4可以看出,囊壁材料的应力分布图类似于同心圆结构,在最中间的一圈区域上有较大的应力,在0.08 μm形变位移量下,应力可以达到1.19~1.29 MPa,而在形变拉伸量减小一半时,其应力值范围也随之相应减小。因为Mises应力是标量,无法从上述云图中得知微胶囊囊壁的各个区域是受拉还是受压,亦无法分析哪种应力占主导,所以对X、Y、Z 3个方向的应力进行分析,结果如图5~7所示。
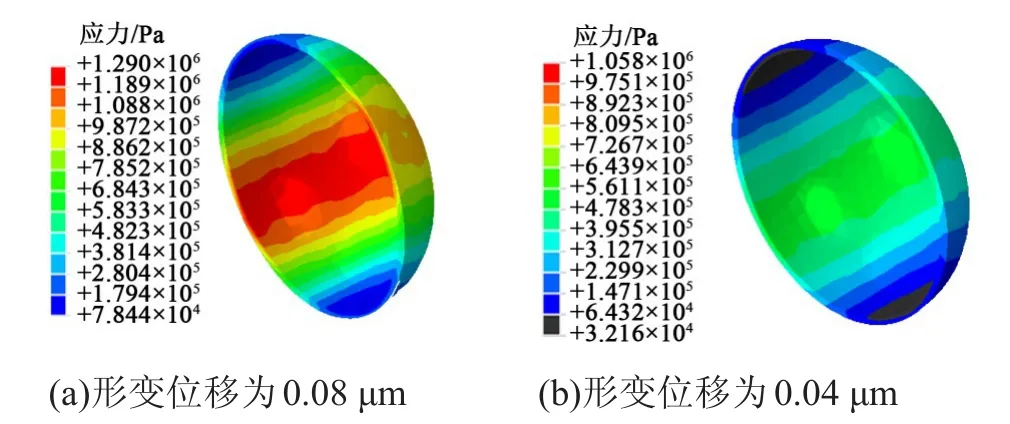
图4 微胶囊壁拉伸等效应力分布云图Fig.4 Cloud charts of tensile equivalent stress distribution of microcapsule wall
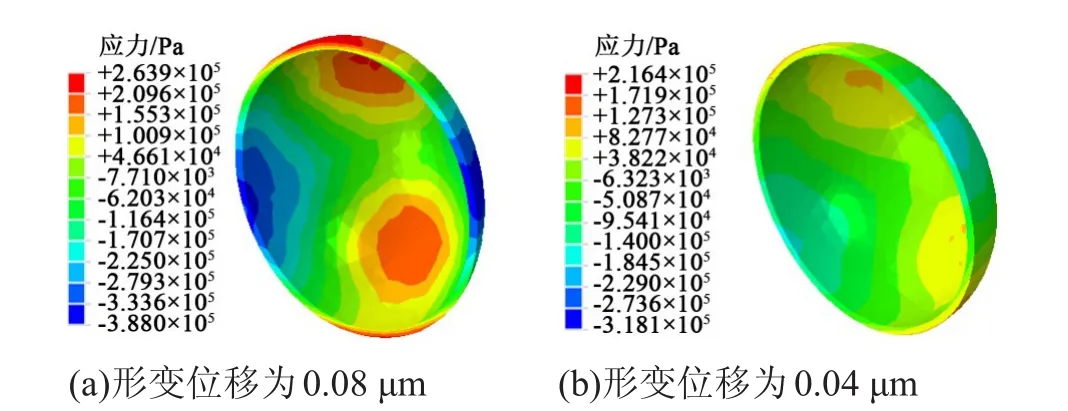
图5 微胶囊壁拉伸X方向上的应力分布云图Fig.5 Cloud charts of stress distribution in the X direction of microcapsule wall
由图5可以看出,在囊壁材料外侧的接触区域产生了较大的拉应力,而内侧区域的最大拉应力明显小于外侧。同时,微胶囊壁中间受到压应力,且最大压应力大于最大拉应力。
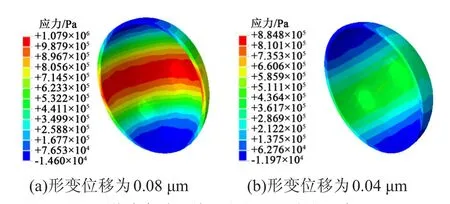
图6 微胶囊壁拉伸Y方向上的应力分布云图Fig.6 Cloud charts of stress distribution in the tensile Y direction of microcapsule wall
由图6发现囊壁材料两端受压应力作用,中间受拉应力作用,但两者数值相差不大。
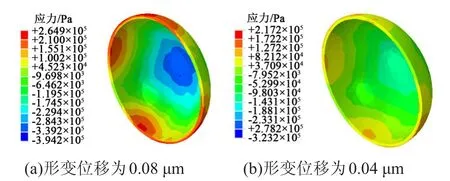
图7 微胶囊壁拉伸Z方向上的应力分布云图Fig.7 Cloud charts of stress distribution in the tensile Z direction of microcapsule wall
由图7可以看出,对比X、Y两个方向的云图,Z方向上的云图更复杂,最大拉应力值集中在囊壁材料外侧的两端,最大压应力值出现在材料内侧的中间区域。同时可以发现,拉应力的变化不是特别大,变化范围为0.1~0.265 MPa。
2.2.2 压缩作用下微胶囊的应力分布状况
图8是微胶囊壁压缩等效应力分布图。从图8可以看出,当形变位移增大时,微胶囊壁各处的位移和应力也随之增大,微胶囊囊壁材料的最大屈服力出现在中间区域。
2.2.3 微胶囊的应力分布状况总结
对比材料拉伸作用和压缩作用下的应力分布状况,可以发现两种情况下囊壁材料的应力分布情况十分相似。图9是两种情况下的应力分布云图。对比图9(a)与(b)可以发现,LDPE基体在拉伸和压缩两种情况下的应力分布是一样的。因此,接下来模型的位移分析和多参数分析均只研究在压缩形变下的情况。
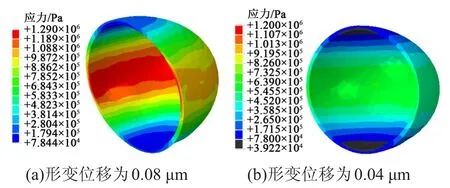
图8 微胶囊壁压缩等效应力分布云图Fig.8 Cloud charts of equivalent stress distribution in compression of microcapsule wall
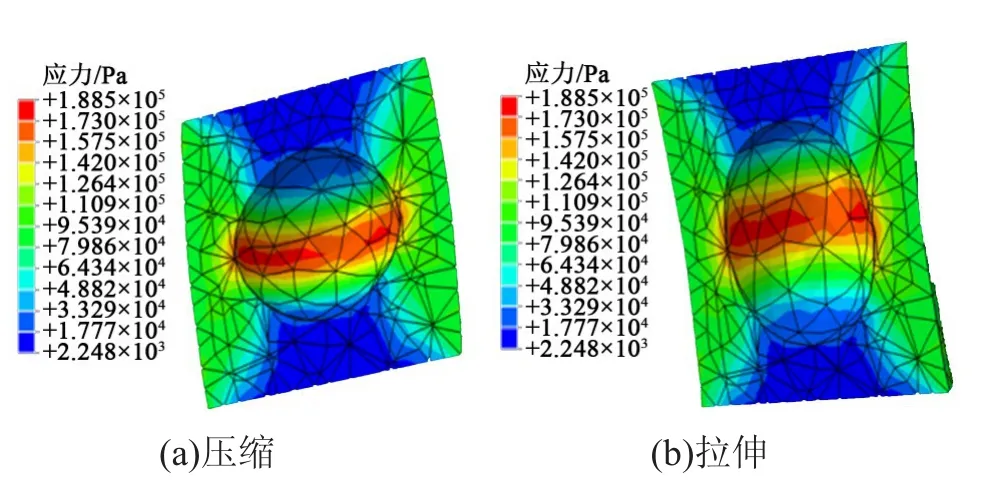
图9 LDPE基体两种情况下的Mises应力分布云图Fig.9 Clouds charts of Mises stress distribution in LDPE matrix
2.2.4 不同形变下微胶囊的位移分布状况
选取X和Y方向上的空间位移来分析,其中X方向上的位移分布如图10所示。从图10可以看出,囊壁材料在X方向上的最大位移为0.015 6 μm,且在微胶囊壁最外端。通过对比形变为0.08 μm和0.04 μm两种情况下位移云图的位移数值,可以发现在X方向上各个点的位移与形变大小成比例。从图10还可以看出,微胶囊壁内、外侧的位移存在一定差距,这是因为外层囊壁材料直接接触基体且与基体有相互作用,而囊壁内侧无接触,造成微胶囊内、外侧材料X方向上的位移不同。
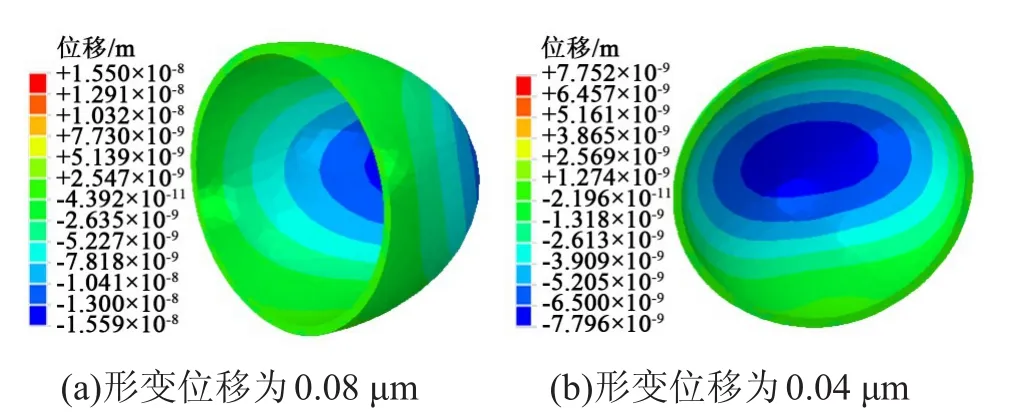
图10 微胶囊壁X方向上的位移分布云图Fig.10 Cloud charts of displacement distribution in X direction of microcapsule wall
为进一步分析囊壁上各点的位移情况,选取囊壁上的几个点,并作了位移-时间曲线图,分别如图11和图12所示。
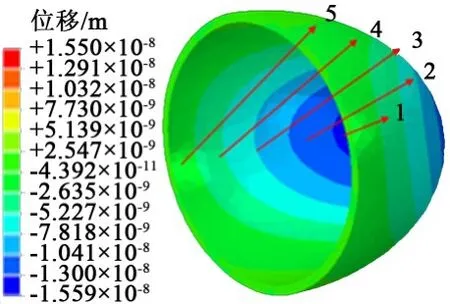
图11 囊壁选点示意图Fig.11 Schematic diagram of selecting points on capsule wall
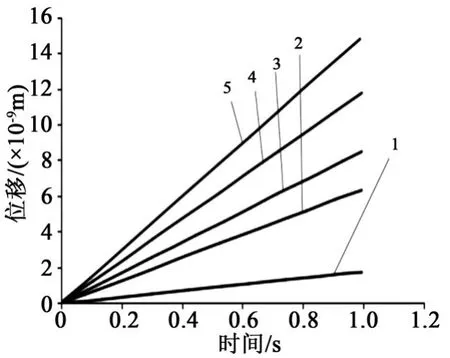
图12 X方向的位移曲线图Fig.12 Displacement curves in X direction
从图11和12可以看出,越靠近Z轴的点,其在X方向上的位移越小,反之则越大。图中5个点的位移曲线均为直线,说明微胶囊的形变是连续均匀的。
图13是微胶囊囊壁材料在形变过程中Y方向上的位移分布云图,从图中可以看出微胶囊壳上部区域的位移总是要大于下部区域。因为在仿真时是下部固定,上部施加位移,所以这一结果是合理的。对比不同位移形变下两者在Y方向上的位移,可以发现其位移仍然成一定比例关系。
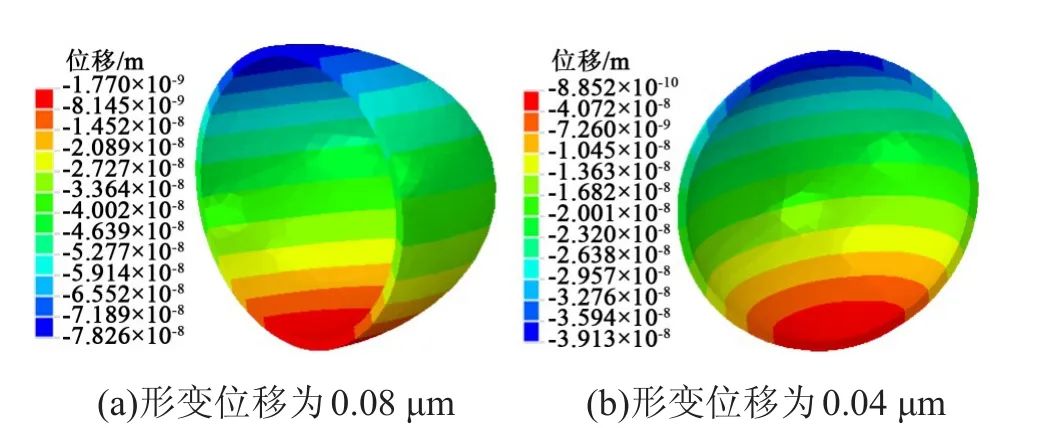
图13 微胶囊壁Y方向上的位移分布云图Fig.13 Cloud charts of displacement distribution inY direction of microcapsule wall
2.2.5 微胶囊的总体分析
通过以上分析可知,微胶囊囊壁材料中间是应力最大区域,即主要承载部位,上下两端一般承受的压力较小。最大应力处不一定是最先破坏的地方,需结合第一强度理论分析。
根据仿真结果取了囊壁上多个内侧和外侧的点,记录其应力大小以及其与微胶囊上端点的距离,如图14所示。
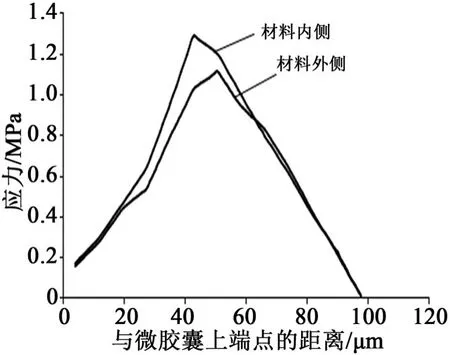
图14 囊壁材料内外侧主应力变化曲线Fig.14 Change curves of main stress on the inside and outside of the wall material
从图14可以看出,囊壁材料内外侧所受应力的大小不同,囊壁内侧区域所受应力普遍大于外侧所受应力,同时囊壁内、外侧应力最大值区域也不一致。预测微胶囊可能破裂的位置大概为图15圆圈内所示区域且为内侧先出现损伤。
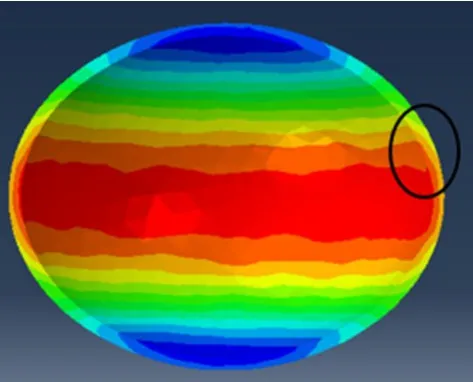
图15 微胶囊可能首先破裂的区域Fig.15 Areas where microcapsules may first break
2.3 微胶囊模型的多参数综合分析
微胶囊整体的机械强度与微胶囊囊壁材料的杨氏模量、微胶囊大小和微胶囊囊壁厚度等有关。在电缆绝缘层受力下,应使微胶囊在具有可裂性的前提下,尽量保持较高的力学性能。因此,分别研究3个因素对微胶囊受力的影响。
2.3.1 囊壁材料杨氏模量对微胶囊受力的影响
首先建立微胶囊囊壁材料杨氏模量为1 GPa和2 GPa的两个模型,保持其他参数不变进行仿真,应力分布和Y方向上的位移分布分别如图16和图17所示。
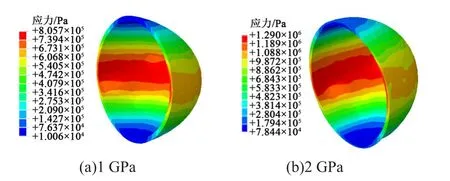
图16 微胶囊囊壁材料不同杨氏模量下的应力分布云图Fig.16 Cloud charts of stress distribution of microcapsule wall material under different Young’s modulus
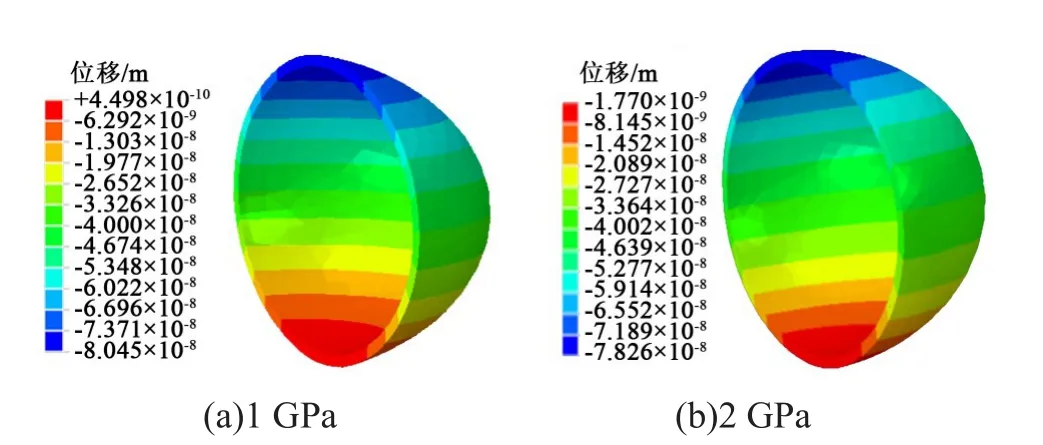
图17 微胶囊囊壁材料不同杨氏模量下Y方向上的位移分布云图Fig.17 Cloud charts of displacement distribution in Y direction under different Young’s modulus of microcapsule wall material
从图16可以看出,随着杨氏模量的减小,微胶囊的主应力相应减小,最大主应力从1.29 MPa减小为0.806 MPa。从图17可以看出,当材料杨氏模量增加时,微胶囊的压缩形变量显著降低。
综合上述分析可知,虽然杨氏模量的提升对微胶囊刚度的加强有帮助,但却造成了局部应力集中的提升过快,因此很难准确判断微胶囊壁弹性模量对微胶囊抗裂性的效果。
2.3.2 囊壁材料杨氏模量对微胶囊受力的影响
微胶囊的直径是微胶囊最直观的参数,本研究针对直径分别为80、100、130、150 μm的微胶囊进行仿真分析,微胶囊囊壁材料的杨氏模量保持为2 GPa,微胶囊厚度保持为3 μm不变。但在改变微胶囊直径大小之后,也改变了微胶囊在LDPE内的体积占比,与控制变量法的原则矛盾。因此,同时改变LDPE基体的大小,以保持体积占比相同。测试结果如图18~19所示。
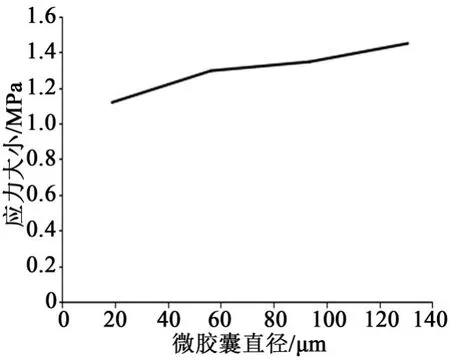
图18 应力最大值-微胶囊直径曲线图Fig.18 Maximum stress-microcapsule diameter curve
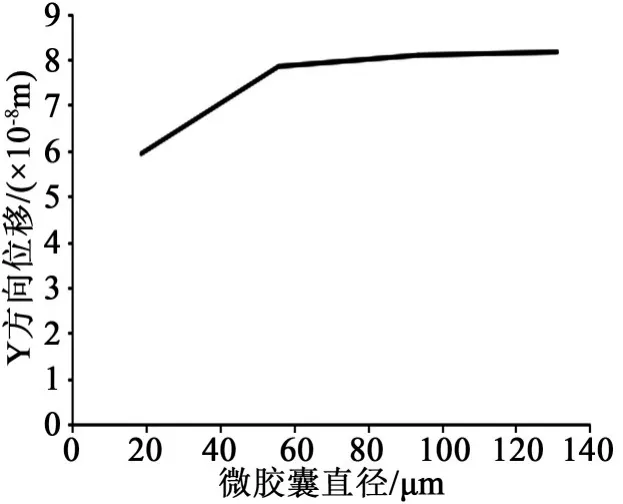
图19 Y方向最大位移-微胶囊直径曲线图Fig.19 Curve of maximum displacement-microcapsule diameter in Y direction
从图18~19可以看出,当直径增大后,表面的应力变化范围变大,且变化更加剧烈,同时在Y方向上的位移变大,可见微胶囊尺寸变大对其力学性能不利。
2.3.3 微胶囊囊壁厚度对微胶囊受力的影响
选择直径为100 μm,囊壁厚度分别为3、4、5、6 μm的微胶囊数值模型,保持其他参数不变,囊壁材料的杨氏模量取值为2 GPa进行微胶囊受力测试,结果如图20~21所示。
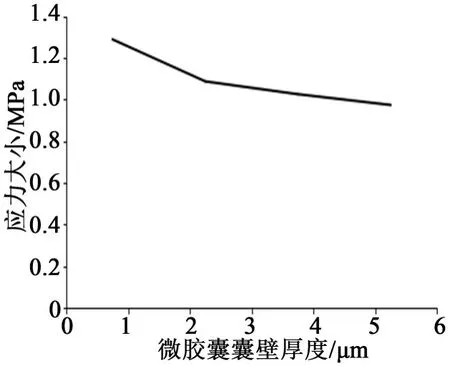
图20 最大主应力-微胶囊囊壁厚度曲线图Fig.20 Maximum principal stress-microcapsule wall thickness curve
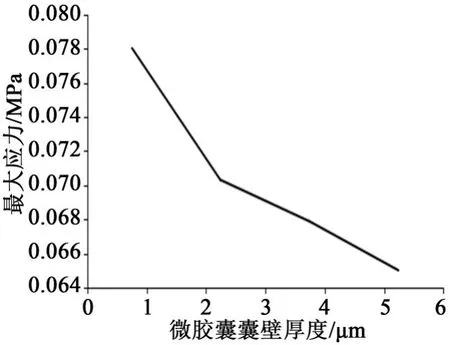
图21 Y方向最大位移-微胶囊囊壁厚度曲线图Fig.21 Maximum displacement in Y direction-microcapsule wall thickness curve
综合分析图20~21可知,当微胶囊的囊壁厚度增加时,微胶囊上最大主应力和Y方向的最大位移量均在减小,并且其减小的速度越来越慢。
通过以上分析可知,在微胶囊复合材料的生产中,可以通过改变制备工艺增加微胶囊的囊壁厚度,以此来提高微胶囊本身的力学性能。同时,由于随着厚度增加,微胶囊的抗裂性增长会变缓,故应根据工程实际选取最佳厚度。
3 结论
(1)囊壁材料在不同方向上的屈服极限是不同的,当应力是沿厚度方向时,囊壁材料的抵抗能力更好。
(2)微胶囊壳应力最大的区域为囊壁内侧且中间部位偏上,该部位也是最容易破裂的。
(3)在一定范围内,微胶囊壳越厚、微胶囊直径越小,微胶囊越不容易发生破裂。
