基于等裕度的60 kV油纸套管纵绝缘优化
2020-12-07刘道生陈星蓉赵子明
刘道生,陈星蓉,赵子明
(江西理工大学 电气工程与自动化学院高电压与绝缘技术实验室,江西 赣州 341000)
0 引言
油纸电容套管是变压器的核心部件之一,作为变压器出线装置,其绝缘性能将直接影响到变压器的稳定运行[1]。套管故障大多由绝缘部分在工作中不断劣化或出现结构缺陷所致,如末屏放电和局部放电缺陷导致绝缘老化,以及电容屏间的热效应等,最终导致绝缘击穿,这些问题一直困扰着生产厂家,威胁现场设备的安全运行[2-5]。针对这些问题,应对套管绝缘结构进行优化设计,以提高其电气绝缘性能。
绝缘结构的优化主要基于其电场分布计算,有限元数值分析是计算电容套管等复杂结构电场分布的有效手段之一[6]。文献[7]基于有限元仿真分析,应用RBF神经网络与NSGA-Ⅱ混合算法对套管的绝缘结构参数进行优化,使关键位置处的场强值达到最优;文献[8-10]讨论了交流复合套管和SF6充气套管的内部屏蔽优化,获得了理想的内外电位和电场强度分布;文献[11]对油浸纸套管电容芯子极板边缘进行优化,改善了边缘场强分布;文献[12]对油纸套管的瓷套进行优化,提高了均压球表面及尖角电极附近区域的绝缘裕度。但以上设计方法均未涉及内部电容式芯子由其导杆到外屏的层间绝缘,即纵绝缘的电气性能优化。文献[13]对穿墙套管进行等裕度优化设计并进行场强分布计算分析,结果表明等裕度设计可提高穿墙套管的局部放电起始电压和均匀内部绝缘电场分布。电容式套管的等电容与等裕度计算方法已有应用,但低局放油纸电容套管的等裕度设计优化及其相关计算分析,还需进一步研究。
本文对60 kV油纸电容套管的电容芯子设计方法进行讨论,研究套管等裕度优化过程。利用ANSYS有限元仿真分析软件对等电容、等厚度、等裕度3种设计方法下的套管芯子模型进行电场仿真,分析比较3种设计方法的电容芯子场强分布,得出最优设计方案。通过设计与制作等效模型对参数计算方法进行实验验证,证明等裕度优化设计方案的可行性。
1 油纸电容套管绝缘设计
目前在60 kV及以上电压等级的高压电力设备中,广泛采用电容式套管,其在变压器中起着引流、绝缘以及机械支撑作用。油纸电容套管的主要结构有上、下绝缘瓷套、法兰(连接套筒)、内部电容芯子和其他附件,中心导电杆和法兰之间的电容芯子作为套管的纵绝缘,决定着电容套管的整体电气性能[14-15]。套管电容芯子的绝缘结构如图1所示,其结构整体对称,图1中左侧为套管芯子的剖视图,右侧为套管电容芯子主视图。各层电容极板均包裹在绝缘纸内,用于强制均匀其内部电场分布,最内层极板紧贴导杆[16]。
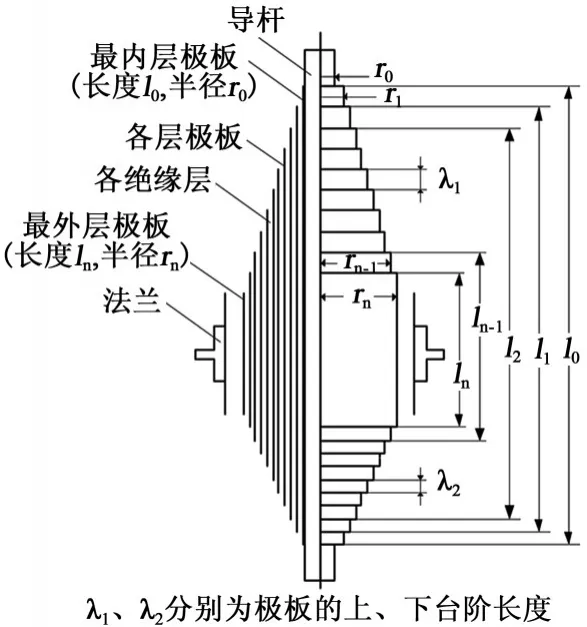
图1 套管电容芯子的绝缘结构Fig.1 Insulation structure of capacitive core for the bushing
1.1 极板结构参数
电容芯子内部由导杆至外屏方向的径向场强Er和芯子外部沿其阶梯方向的轴向场强Ea都取决于电容芯子的各极板半径和长度,合理设计各层极板的径向与轴向尺寸可使套管芯子径向与轴向场强均匀,并缩短套管半径及长度[16]。
若忽略电容芯子中的边缘效应,则各均压极板通过的电通量不变,其基本关系为式(1)。

式(1)中:D为电位移量,C/m2;εr为绝缘材料的相对电容率;ε0为真空电容率,其值为8.854×10-12F/m;A为极板面积,m2;r为极板的半径,m;l为极板的长度,m。
若保持径向场强Er不变,则由rl=c(常数)可得式(2)。

由式(2)可知,Eα与r2成正比,使得轴向场强分布不均匀,套管设计长度过长,通常不选用该方案。
若保持轴向场强Eα不变,可得式(3)。
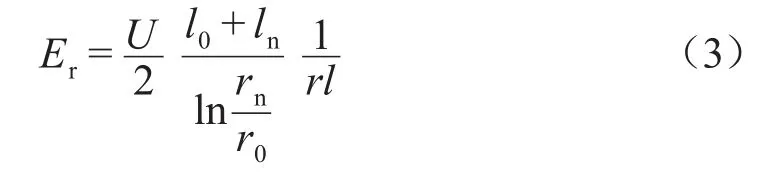
式(3)中:U为套管最大工作电压,kV;l0为最内层极板长度,mm;ln为最外层极板长度,mm;r0为最内层极板半径,mm;rn为最外层极板半径,mm。
因为极板半径r和长度l的变化相反,Er较为均匀,所以选用轴向场强不变的设计方法对高压套管极板进行设计。
1.2 等电容绝缘结构
通过最小绝缘厚度设计,确定油中极板边缘放电的电压值,计算极板边缘局部放电起始场强。根据设计绝缘裕度得出径向最大许用场强,以此确定该电压等级下电容套管的设计层数。在保证芯子上、下部位不发生轴向闪络的情况下,根据上、下瓷套长度得出上、下台阶长度,以场强分布均匀和减小材料消耗为设计原则,计算出各层极板长度,以缩小套管整体尺寸。
实际生产中,通常采用等电容原则来设计极板半径,使各绝缘层间的电容和电压相同,绝缘层间的绝缘设计厚度不同[17]。
等电容设计时,任一层极板的电容值Ck如式(4)所示。
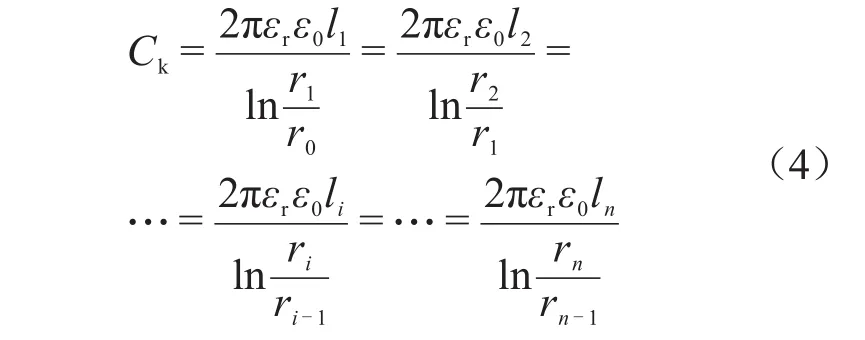
1.3 等厚度绝缘结构
等厚度设计使得每层绝缘极板厚度相同,每层局部放电起始电压相同并高于等电容设计最小值,优化了边缘两侧绝缘层的局放起始电压。绝缘层厚度可由式(5)确定。

等厚度设计中,各层绝缘厚度相等,方便生产卷制,各层局部放电起始电压相同,但各层电压分布和局放裕度极不均匀。
1.4 等裕度绝缘优化设计
基于等电容和等厚度两种设计方法,文中引出套管芯子的等裕度设计概念。套管内绝缘芯子的整体局部放电起始电压主要取决于各绝缘层中的最小局放裕度。等裕度设计依据等电容设计原理,在芯子绝缘层数n不变,轴向场强Eα的分布及芯子整体尺寸不变的情况下,合理调整各层绝缘厚度,使各绝缘层所分担的电压和该绝缘层的局放起始电压之比近似相等,即各绝缘层的局放裕度相等。提高电容芯子的整体局放起始电压,保证套管设计的经济合理性及可靠性[15]。
等电容设计下的套管芯子整体尺寸已确定,绝缘层数及各极板上、下台阶长度λ1x、λ2x已知,则电容芯子上部与下部轴向电场强度Eα1、Eα2分别为式(6)和式(7)。
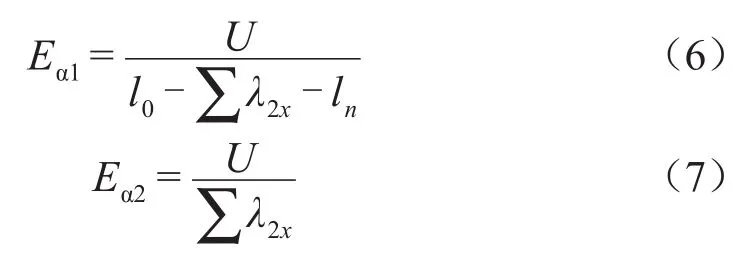
式(6)~(7)中:U为套管最大工作电压,kV。
由等电容设计原理所得的每一层极板的长度与半径,作为等裕度设计中各层极板长度与半径的初始值,由此得到每一层的电压值ΔU、上下台阶长λ1、λ2以及第x层极板的长度lx,如式(8)~(11)所示。
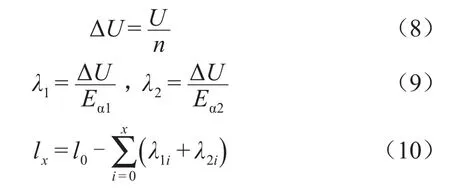
当轴向场强Eα分布均匀时,套管极板的包络线方程为式(11)。
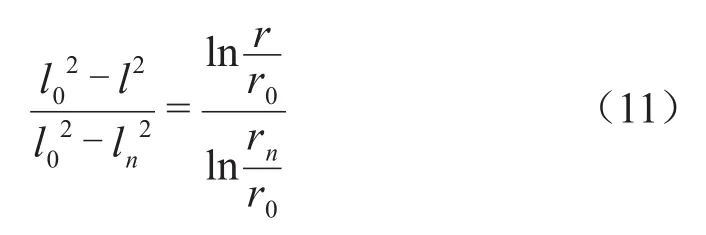
由式(11)解得各极板半径rx为式(12)。
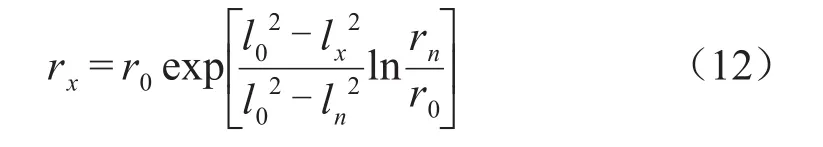
由式(3)可得该层径向场强Erx为式(13)。
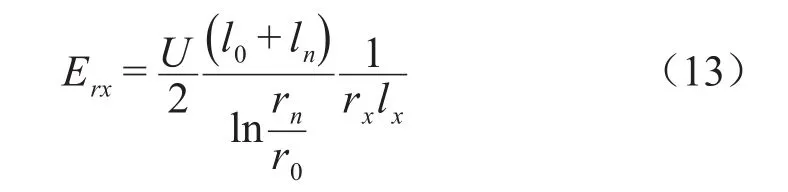
由式(13)可知,径向场强的分布几乎与绝缘厚度无关,按等裕度设计时的各极板径向场强也几乎不变。等裕度设计中,假设各极板处的径向电场近似等于由初值计算的Erx,各绝缘层的局部放电起始电压ΔUpx与工作时分配到该层的电压ΔUx之比应为一常数,如式(14)所示。
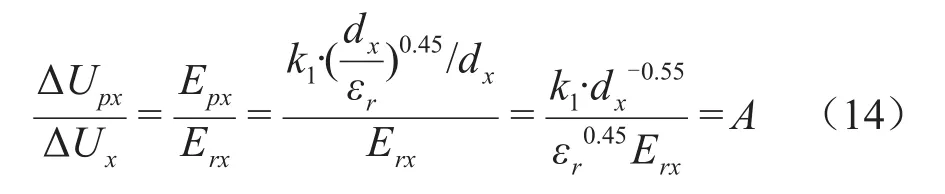
式(14)中:Epx为第x层的局部放电起始场强,kV/mm;k1为油中极板起始局部放电时的经验系数;dx为第x层的绝缘厚度,mm;εr为绝缘材料的相对电容率。将各层绝缘厚度之和表示为外屏与导杆半径之差,并通过式(14)代换dx可得式(15)。
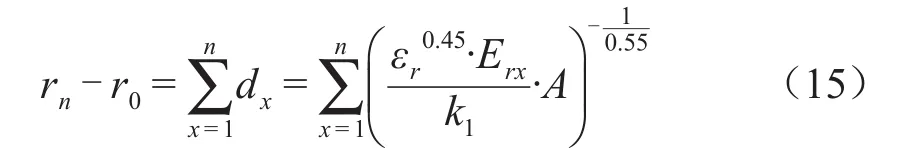
式(15)中:rn-r0为电容芯子绝缘厚度。由式(15)推导出常数A的表达式为式(16)。
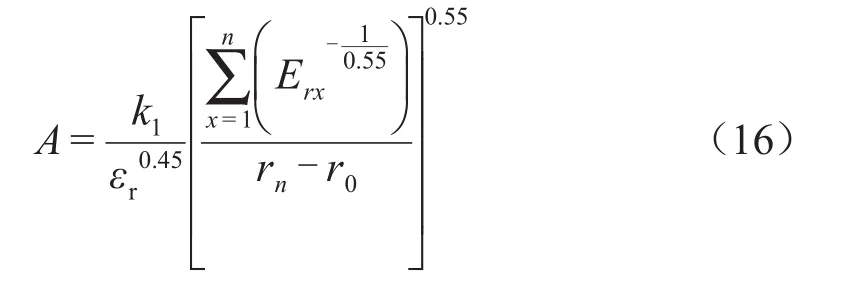
计算并得到新的rx、Erx、lx、ΔUx、λ1x、λ2x。由式(14)得第x层绝缘厚度为式(17)。
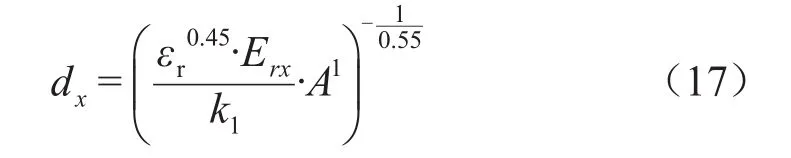
式(17)中:A1为式(16)的计算结果。更新后的各层极板半径rx和长度lx分别为式(18)和式(19)。

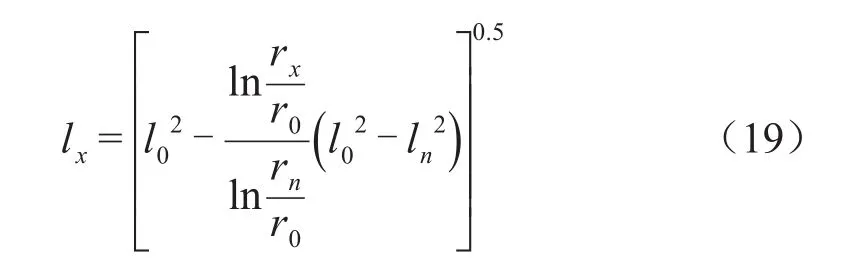
将更新后的极板半径及长度代入式(13),重新计算Erx。其优化计算流程图如图2所示。
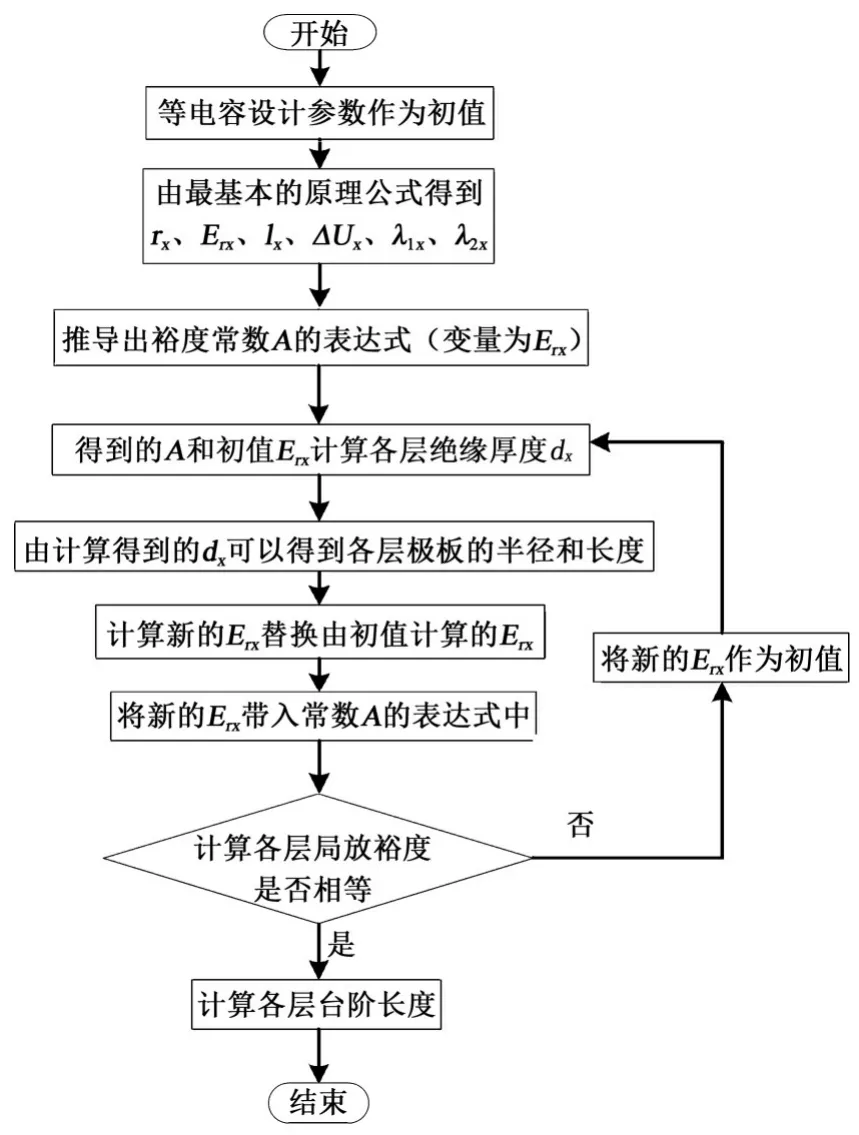
图2 等裕度优化流程图Fig.2 Flow chart of equal-margin optimization
等裕度优化设计中,经过循环计算后各绝缘层裕度的优化效果如图3所示。
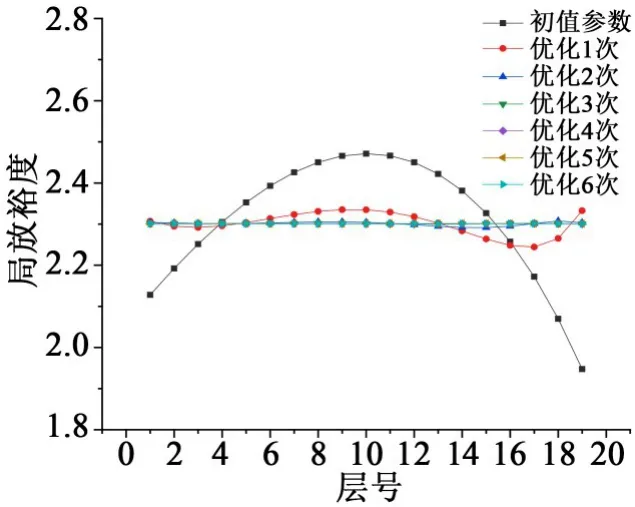
图3 套管芯子绝缘层的局放裕度优化图Fig.3 Optimization diagram of partial discharge margin of bushing core insulation layer
图3表明,随着优化次数的增加,绝缘层的局放裕度分布从初值参数的抛物线分布,逐渐变化为优化6次时的水平直线分布,即各层局放裕度趋近同一值,且各极板尺寸变化越来越小,直至电容芯子各绝缘层裕度值相等。等裕度设计中,各层局放裕度都相等且高于等电容和等厚度设计中的最小局放裕度,而电容芯子整体的局放起始电压与最小局放裕度有关,因此能提高套管的局部放电起始电压。
2 套管电场仿真分析
套管结构具有高度对称的特点,其内部层间绝缘电场分布具有二维轴对称结构。因此将三维套管模型简化为二维轴对称模型,将三维电场化为二维电场进行分析,且对计算精度和结果影响不大[18]。
采用ANSYS有限元仿真分析软件,针对套管内部绝缘结构与关键尺寸建立有限元模型,并对套管内部电势和电场分布情况进行分析,获得套管的电势和电场分布规律[18-19]。为模拟电容套管正常工作时内部芯子的电场分布情况,在中心铜棒上施加60 kV电压,末屏及边界法兰处为零电位;为保证油浸绝缘纸中的金属极板正常工作,在各层极板处添加悬浮电位。模型分析中主要材料的相对介电常数如表1所示。

表1 材料的相对介电常数Tab.1 Relative permittivity of the materials
套管场强分布如图4所示,沿图路径a-b的径向场强分布曲线如图5所示。图5中最左侧为金属导电杆,其内部场强基本为零,导杆上下两端与绝缘油接触,油中场强上升。绝缘层中介质为油浸绝缘纸,电场分布为中间低两侧高。
3种设计方法得到的套管的径向场强分布如图6所示。从图6可看出,3种套管的径向场强分布规律相同,但等电容设计的套管径向场强分布不均匀,尤其是在最外层极板处电场畸变较大;等厚度设计的套管径向场强在最外层处分布更为均匀,但最内层与最外层场强差距过大,导致绝缘内部场强分布不均;而等裕度设计的套管径向场强分布比前两者都更为均匀,且场强峰值有所下降。
在导杆中加载电压,得到其局部放电起始场强最大值,与理论计算值进行对比,结果如表2所示。从表2可以看出,理论计算结果与仿真结果相符。
根据表2可知,等裕度设计方案将60 kV油纸电容套管的整体局部放电起始电压在等电容设计的基础上提高了12.36%。

图4 套管芯子浸于油中工作时的电场分布Fig.4 Electric field distribution of bushing core immersed in mineral oil

图5 径向场强分布曲线Fig.5 Radial field intensity distribution curve
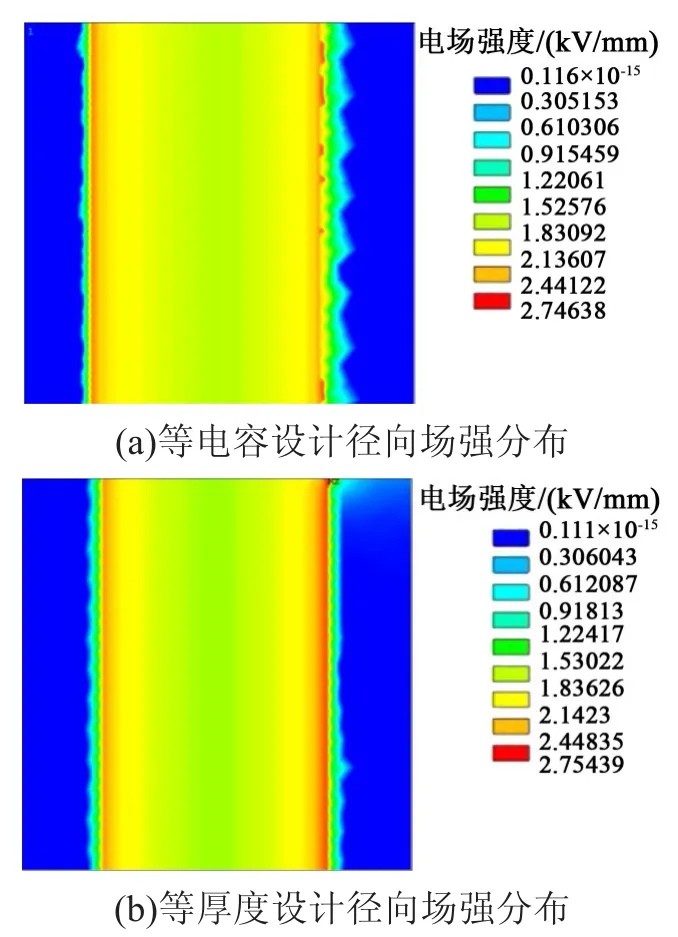
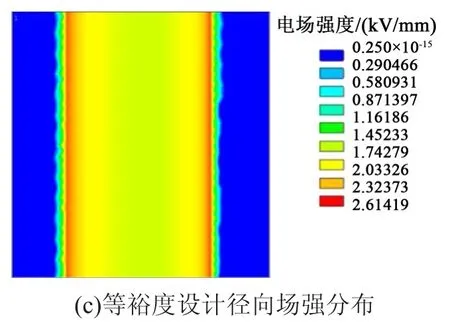
图6 套管的径向场强分布图Fig.6 Radial field intensity distribution patterns of bushings
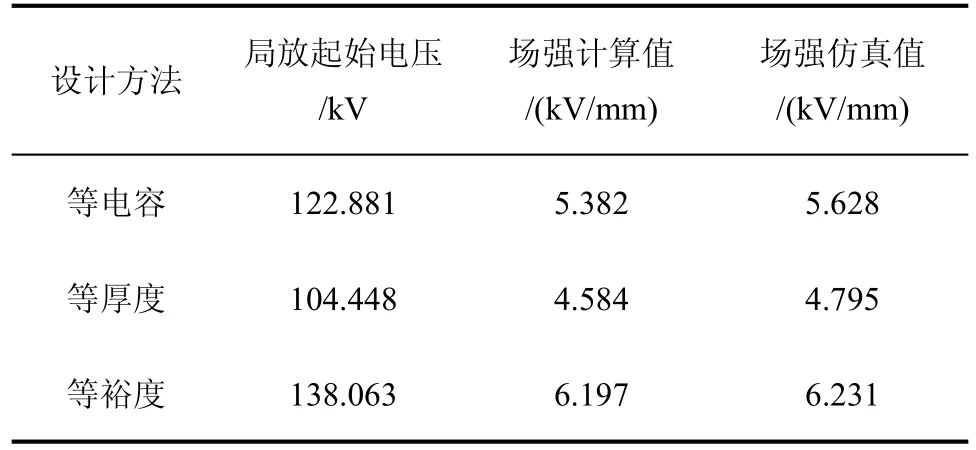
表2 局放起始电压和场强的计算与仿真结果Tab.2 The calculation simulation results of initial partial discharge voltage and partial discharge field intensity
3 等效模型实验
3.1 模型制作
依据前文所述设计方案和计算步骤,设计出等电容、等台阶、不同绝缘层厚度结构的电容芯子模型,使其结构参数和场强分布与实际60 kV模型等效。等效模型采用手工卷制,按照计算出的结构参数,控制极板长度和半径。卷制时将铜箔电极和电缆纸交替缠绕在直径为6 mm的铜导杆上,绝缘层采用厚度为0.01 mm的电缆纸缠绕而成,达到各绝缘层设计厚度要求为止。
3.2 实验数据测量及分析
模型制作完成后进行真空干燥48 h,之后用变压器油浸渍,除去套管芯子与容器内水分和气泡,干燥温度为105℃,真空度为50 Pa。干燥处理后的模型如图7所示,等效芯子模型浸于变压器油中,容器外部铜箔模拟实际套管外部法兰,以方便测试时接地。通过对等效模型的电压值、电容值及场强分布进行实验测量,验证模型参数计算的合理性与正确性。
芯子的电容值采用高压介质损耗测试仪测量,测量电路采用正接线法,如图8所示。

图7 等效实验模型Fig.7 Equivalent experimental model

图8 电容测量正接线图Fig.8 Positive circuit diagram of capacitance measurement
层间电压测量中施加电压为模型折算的实际工作电压19.4 kV,所测电压为各层极板对地电压,测量接线图如图9所示。
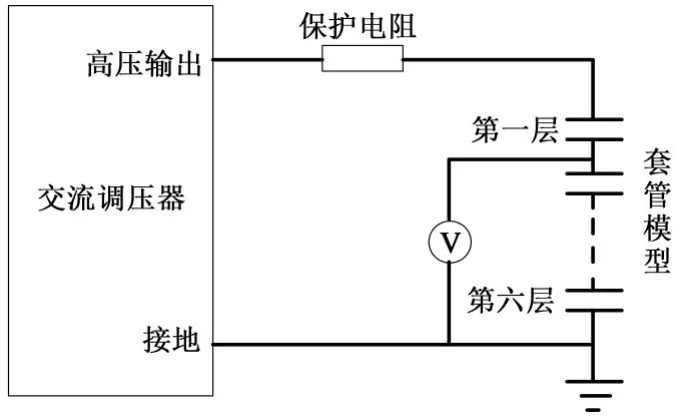
图9 层间电压测量接线图Fig.9 Circuit diagram of interlayer voltage measurement
模型测量电容值如表3所示。从表3可以看出,3次实验测量值与理论计算电容值相差不大。
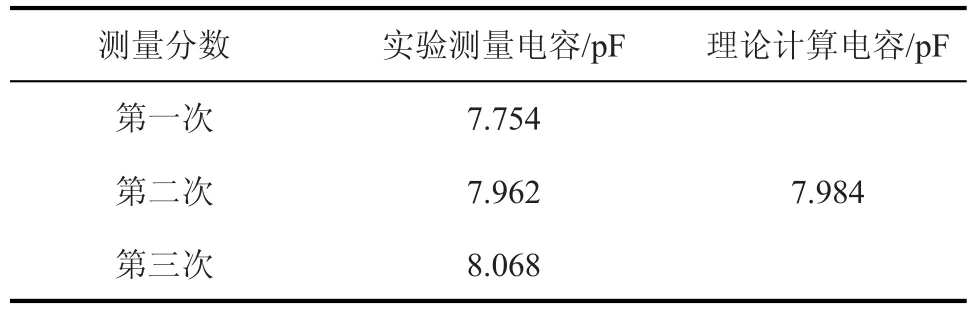
表3 电容测量结果Tab.3 Capacitance measurement results
模型各层电势分布如图10所示。从图10可以看出,实验值与计算值相比相差不大,皆由内至外呈线性下降。

图10 层间电压测量结果Fig.10 Measurement results of interlayers voltage
等效模型中,由实测电压得出各绝缘层的场强分布结果如图11所示,电容芯子的外屏与内屏的场强较高,中间部分场强较低。实测电压与计算电压之间存在差异,但实测场强与计算场强分布规律相同且数值相近。说明本文的计算方法可行,各项参数符合套管实际运行工况。
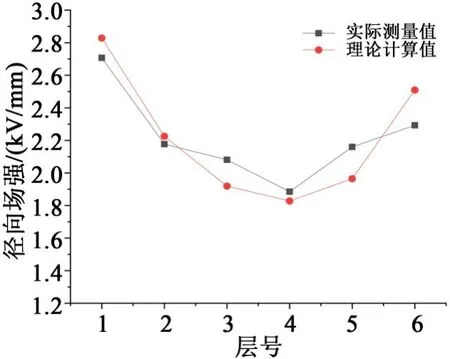
图11 场强测量结果Fig.11 Field intensity measurement results
4 结论
(1)等裕度优化设计使套管芯子各绝缘层的局放裕度相同,且高于等电容设计的最小局放裕度。在60 kV油纸电容套管原设计基础上,使其局部放电起始电压设计值提升了12.36%。
(2)通过有限元计算分析和等效模型试验可知,等裕度优化设计提高了套管电容芯子的局放起始电压,优化了芯子径向场强分布,验证了套管模型参数计算的合理性。
