矿石图像受空间域图像增强算法的影响研究

杨 震，段 云

(1.矿冶科技集团有限公司，北京 100160；2.北京矿冶研究总院，北京 100160)

矿岩图像分析方法是国内外岩石块度统计工作中应用的主要方法[1]。该方法的优点在于能够直观反映爆堆的粒级分布，应用相机、计算机、网络传输，工作量小，劳动强度低，结果便于分析统计。但矿岩图像分析技术依旧存在很多技术难点，矿山拍摄条件复杂，拍照时对比度低，存在噪声干扰等不确定性因素的影响[2]。图像处理难度较大，在图像处理过程中选用合适的图像增强方法可以有效提高矿石识别精度，同时优化图像处理过程，提高图像处理效率。

图像增强是图像处理过程中提高计算精度的关键环节，通过适当的图像增强算法，可以有目的地增强图像的整体或局部特征，抑制不感兴趣的区域，扩大图像中不同特征之间的差别，改善图像质量，加强图像判读和识别效果，使图像更满足分析或机器决策的需要，是整个图像处理系统中关键的一部分[3]。

1 空间域图像增强

图像增强算法根据处理过程中所在的空间不同，可分为基于空间域的算法和基于频率域(变换域)的算法两大类。常用的图像增强算法为空间域的点运算和邻域运算。点运算直接对像素灰度进行点对点映射，常见的点运算包括灰度变换、直方图匹配(修正)和直方图均衡以及某些图像的算数或逻辑运算等。图像的邻域增强则以某一像素为中心，综合该像素及其周围某一范围(邻域)像素灰度值进行计算，并将计算结果作为中心像素新的灰度值[3]。本文选用几种常用的图像增强方法对图像进行处理，然后对结果进行比较，并验证其鲁棒性，选择适用于本系统的图像增强方法。

1.1 空间域点运算图像增强方法

常见的空间域点运算包括灰度变换、直方图匹配(修正)和直方图均衡，以及某些图像的算术或逻辑运算等。

直方图均衡常用于调整图像对比度，适用于有用数据对比度相当接近的情况，直方图均衡优点在于能以较小的计算量突出图像的细节，且能实现可逆操作[4]。其原理是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布[5]。其操作是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同。其过程本质上是通过扩大灰度量化间隔来扩展图像中像素数较多的灰度级，压缩像素数较少的灰度级来实现的。直方图均衡可用于增强那些未使用所有灰度级的图像动态范围，提高其整体对比度。

图像灰度变换是以点对点映射的方式将原图像的像素灰度值变换为新的灰度值。由于像素的新灰度值仅由原像素的灰度和灰度变换函数决定，因此灰度变换并不会改变像素点之间的空间关系。假定输入图像为SrcA(x,y)，输出图像为Dst(x,y)，则图像灰度变换可由式(1)表示：

Dst(x,y)=GST[SrcA(x,y)]

(1)

1.2 邻域运算滤波图像增强方法

1.2.1 邻域增强和卷积

图像的邻域增强，就是在空间域对其进行高通或低通滤波，以消除其中的噪声，锐化图像的轮廓，沿某一方向锐化目标的边缘等。图像的空间域滤波直接根据像素及其周围邻域内的像素值，通过某种计算或变换得到新的像素值来实现滤波功能。如果输出像素是输入像素及其邻域像素的线性组合，则称为线性滤波，否则称为非线性滤波。基于卷积的图像邻域加权求和滤波就是一种空间域的线性滤波方法，而中值滤波等非加权计算形式的滤波则称为非线性滤波。

卷积运算是通过在图像中滑动一个模块，不断根据邻域像素的值计算各个像素的新值来完成计算过程。卷积运算是积分运算，其反映了函数h(τ)被反转成h(-τ)后，沿τ轴在另一个函数f(τ)上移动时，与其所重叠部分的积分。对于离散信号来说，假定有两个长度分别为m和n的序列f(i)和h(j)，则他们的积分将输出长度为(m+n-1)的序列，可表示为式(2)：

(2)

若线性时不变系统为二维系统，则可表示为以下连续和离散形式：

连续形式为式(3)：

g(x,y)=f(x,y)h(x,y)

(3)

离散形式为式(4)：

(4)

如果二维线性系统可分离，即h(x,y)=h1(x)h2(y)，则线性系统可分解为两个一维卷积，如式(5)所示：

g(x,y)=h(x,y)f(x,y)

(5)

离散形式如式(6)：

(6)

在实际进行二维卷积计算时，可以将其分解为连续的两次一维卷积计算，这种分解可以降低程序算法的计算量，提高计算速度。使用一个大小为3×3的卷积核对图像进行卷积运算时的过程如图1所示。

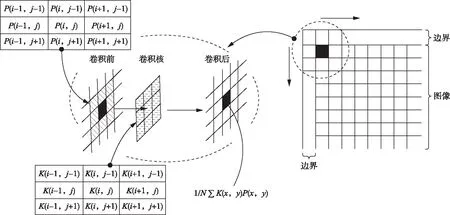
图1 数字图像卷积计算过程Fig.1 Digital image convolution calculation process

1.2.2 线性滤波和非线性滤波

如前所述，邻域增强中的线性滤波基于卷积运算，卷积核的尺寸限定了处理时的邻域大小，卷积核中的元素值设定了各邻域像素对中心像素影响的权重值，其绝对值越大，对中心像素的影响越大。如果卷积核中的因子有正有负，则滤波过程相当于对邻域像素求权重差，其效果相当于高通滤波，而如果卷积核中只有正因子，那么滤波过程相当于邻域像素求权重和，其效果相当于低通滤波[6]。

与线性滤波方法类似，空间域的非线性滤波方法也常用于滤波算子，基于像素的邻域进行计算，但是其计算函数往往并非线性的。例如，非线性梯度滤波和差值滤波过程均基于像素左上方2×2的邻域进行。它们的计算函数分别表示如下：

非线性梯度滤波为式(7)：

(7)

差值滤波为式(8)：

(8)

2 图像增强算法：

如前所述，本文使用的空间域点运算图像增强方法为：

(0)读取原始图像，不进行图像算法增强处理。

1)直方图均衡[7，8]

利用图像直方图对比度进行调整，当图像的有用数据对比度相当接近的时候用来增加图像的局部对比度。

2)对数灰度变换[9]

对数灰度变换拉伸低灰度区域，压缩高灰度区域以及图像整体变亮，其函数表达为y=clog(1+x)，其中c为常数(8位灰度图像可设为107)，其灰度变化函数曲线如图2示。

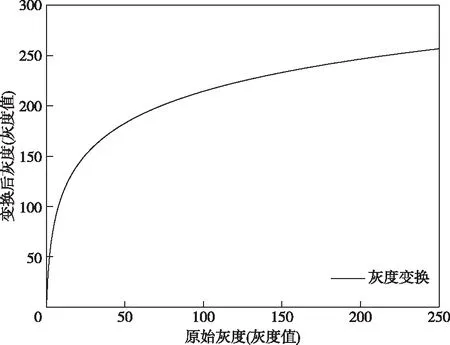
图2 对数灰度变换函数曲线图Fig.2 Logarithmic gray-scale transformation function curve

3)平方变换[9]

平方变换压缩低灰度区域，拉伸高灰度区域以及图像整体变暗，其函数表达为y=cx2，其中c为常数(8位灰度图像可设为0.004)，其灰度变化函数曲线如图3所示。

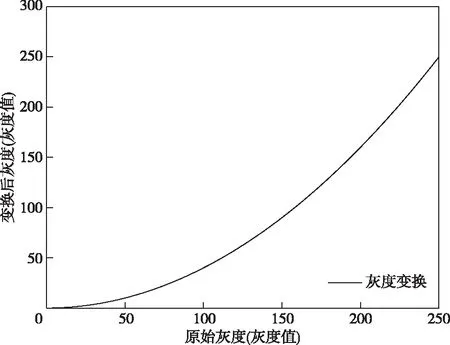
图3 平方灰度变换函数曲线图Fig.3 Graph of squared gray-scale transformation function

4)线性高通滤波梯度算子(3×3)

梯度算子3×3算子结构如式(9)所示：

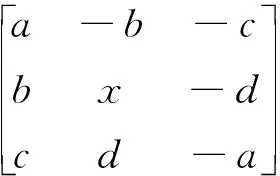
(9)

式中，a、b、c、d为整数，x取0或1，算子卷积核沿45°对角线方向增强边缘，x=0时，仅显示图像灰度变化量，x=1时灰度变化量与原图像叠加，算子尺寸越大，边缘越粗。

5)线性高通滤波拉普拉斯算子(3×3)

拉普拉斯算子3×3算子结构如式(10)所示：

(10)

式中，a、b、c、d为整数，x≥2(|a|+|b|+|c|+|d|)；x=2(|a|+|b|+|c|+|d|)时，仅显示灰度变化量；x>2(|a|+|b|+|c|+|d|)时，灰度变化量与原图像叠加，算子尺寸越大，边缘越粗。

6)线性低通平滑滤波(3×3)

平滑滤波3×3算子结构如式(11)所示：

(11)

式中，a、b、c、d为整数，x取0或1，此算子属于加权均值滤波算子，中心因子为0时，对图像的平滑程度要比其为1时强，邻域内因子的值越大，对中心像素点的影响越大，算子的尺寸越大，对图像的平滑效果越明显。

7)线性低通滤波高斯算子(3×3)

高斯算子3×3算子结构如式(12)所示：

(12)

式中，a、b、c、d为整数，x大于1，属于加权均值滤波，中心因子大于1，因此滤波效果比平滑滤波要柔和，算子内因子以中心点为原点呈正态分布，其值越大，对中心像素的影响越强，算子的尺寸越大，对图像的平滑效果越明显。

8)非线性高通差值滤波[10]

差值滤波其计算原理如图4所示：

图4 差值滤波原理Fig.4 Principle of difference filtering

差值滤波基于像素左上方2×2的邻域进行计算，邻域内像素沿多个方向，两两求差值绝对值的最大值，沿多个方向增强图像的边缘。

9)非线性高通梯度滤波[11]

非线性高通梯度滤波其计算原理如图5所示：

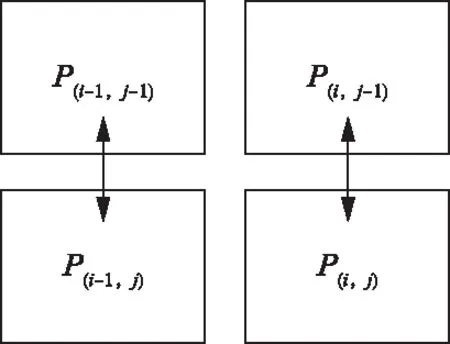
图5 非线性高通滤波原理Fig.5 Principle of nonlinear high-pass filtering

梯度滤波基于像素左上角2×2的领域进行计算，邻域内像素沿垂直方向，两两求差值绝对值的最大值，沿垂直方向增强图像的边缘。

10)非线性低通滤波

非线性低通滤波其计算原理如图6所示。

图6 非线性低通滤波原理Fig.6 Principle of nonlinear low-pass filtering

非线性低通滤波基于像素周围3×3邻域内像素平均值μ和标准差σ计算，像素与μ的差值小于一个标准差σ时保持不变，否则被设置为均值。

11)非线性低通N阶滤波

非线性低通N阶滤波其计算原理如图7所示：

图7 非线性低通N阶滤波原理Fig.7 Principle of nonlinear low-pass N-order filtering

非线性低通N阶滤波对领域内的像素灰度从小到大排序，从排序后的序列中选取序号为N的值为中心像素的新值，所选值小于中值时，将腐蚀亮区域，膨胀暗区域；所选值大于中值时，将腐蚀暗区域，膨胀亮区域。

3 结果对比

3.1 图像处理

矿石图像处理计算过程如图8所示，在全局阈值二值化[12]的过程中阈值设定min=30～65(根据不同方法手动调整)，max=255。在形态学处理断地峡的过程中腐蚀次数设定为7～23次(根据不同方法手动调整)，清除23像素以下颗粒。

图8 矿石图像处理流程图Fig.8 Ore image processing flowchart

使用LabVIEW2018版本程序调用NI Vision工具包，实现图8所示的矿石处理流程，编写的主要程序框图部分如图9所示。

图9 图像处理程序框图Fig.9 Block diagram of image processing program

利用图9所示程序框图中的图像增强部分程序，逐一实验11种图像增强方法，得到的图像增强效果图如图10所示。

根据图10所示结果，各类方法的图像增强效果判定只能给出定性的判断，而无法得到定量的结果。还需对增强处理后的矿石图像进行进一步的处理。根据图8所示的流程图及图9所示程序框图，对增强后的矿石图像进行二值化、形态学处理及颗粒参数显示，其颗粒统计结果如图11所示。

图10 增强算法效果图Fig.10 Effects of the enhanced algorithm

图11 图像增强算法颗粒统计Fig.11 Image enhancement algorithm particle statistics

3.2 结果分析

为定量描述图像增强方法的优劣，提出公式(13)：

(13)

式中：a=准备描述块数，准确描述每块岩石边界的矩形数；b=错误分割块数，只描述部分非完整岩石的矩形数；c=错误粘连块数，描述两块及以上岩石的矩形数；T=误差因子，其值越小代表图像增强效果越好。

将各图像增强效果图中颗粒汇总，结果如表1所示。

表1 图像增强方法统计表

由表1可见，适用于矿石图像的图像增强方法为直方图均衡方法(T=0.5)、线性低通平滑滤波(3×3)(T=0.4)、非线性低通N阶滤波(T=0.6)。

4 结论

通过对比增强后的矿石图像发现，在空间域图像算法中增强图像对比度的直方图均衡方法以及平滑边缘的低通滤波算法，可以有效地提高矿石清晰度。在空间域的图像增强算法中，高通滤波会在增强矿石边缘的同时，增强矿石表面因表面不平滑出现的伪边缘，高通滤波过程中增加了矿石的干扰信息，与之相反，低通平滑滤波更能凸显矿石图像边缘的真实信息。为得到图像增强效果的定量评价，对矿石图像进行二值化、形态学处理、颗粒识别等算法得到矿石参数，提出用T值定量地判断图像增强对矿石图像的影响。得到适用于矿石图像的图像增强方法为直方图均衡方法(T=0.5)、线性低通平滑滤波(3×3)(T=0.4)、非线性低通N阶滤波(T=0.6)。