板式轨道充填层SCC疲劳损伤本构模型

马昆林,万镇昂,龙广成,谢友均

(中南大学 土木工程学院，湖南 长沙 410075)

CRTSⅢ型板式无砟轨道结构是我国具有独立知识产权的轨道结构形式，其中的充填层结构采用自密实混凝土材料，CRTSⅢ型板式无砟轨道结构图[1-2]见图1。通过预埋在轨道板下端的门形钢筋，轨道板与充填层连接而形成复合结构，相比CRTSⅠ型、CRTSⅡ型和双块式轨道结构，CRTSⅢ型轨道结构具有设计更合理、造价低、抗裂性能好等优点。实际工程中，高速列车的运行将对轨道结构将产生动荷载作用，动荷载通过钢轨传到轨道板再作用到充填层，因此充填层SCC将长期受到高速列车的动荷载作用，且由于施工质量波动，温度变化造成的轨道板翘曲变形、离缝等原因，充填层SCC存在薄弱部位，荷载作用下不可避免会出现应力集中，对轨道结构的稳定性以及正常运营不利[3]。我国长江以南地区雨季长，工业发达，由于环境污染部分地区还会出现酸雨。无砟轨道结构长期暴露于自然环境中，该结构特殊的“三明治”结构以及混凝土自身的多孔性，造成了环境水对SCC的侵入速率快但蒸发速率慢，因此充填层SCC的工作状态将是长期高含水率或酸雨侵蚀状态。

图1 CRTSⅢ型板式无砟轨道结构图

陈梦成等[4]发现杂散电流和氯离子多因素侵蚀条件下，钢筋混凝土梁疲劳损伤明显增大。破坏时无征兆。李进洲等[5]运用传统应变片的疲劳试验实时测试系统进行预应力混凝土梁的腐蚀疲劳试验，发现锈蚀预应力混凝土梁在疲劳反复荷载作用下构件的中性轴位置基本保持不变，不像非锈蚀试件那样呈现出明显的“三阶段”变化过程。欧阳祥森等[6]研究主筋锈蚀、混凝土碳化等耐久性损伤后钢筋混凝土梁的疲劳性能时，发现试验梁最大跨中挠度随着锈蚀率的增加和疲劳加载次数的增加逐渐增大，试件梁抗弯刚度显著劣化，提出了临界锈蚀率，建立了基于不同钢筋锈蚀率的锈损钢筋混凝土梁分段线性疲劳寿命预测模型。刘晓春等[7]研究了CRTSⅢ型板式无砟轨道在列车疲劳荷载作用下的应力变形分布规律及疲劳损伤发展形态。长期动荷载作用下将导致混凝土材料的服役性能将逐渐降低[8-9]，无砟轨道混凝土材料在服役过程中，不仅面临高速行驶列车的长期动荷载作用，还将受到雨水特别是酸性雨水的共同作用，因此CRTSⅢ型板式无砟轨道充填层SCC在复杂服役环境下性能的变化与寿命预测还有待深入研究。

本文在基于Helmholtz自由能建立的混凝土本构方程的基础上，采用静弹性模量和残余应变分别对疲劳损伤过程中充填层SCC的刚度退化和塑性变形进行了表征，构建了基于CRTSⅢ型板式轨道充填层SCC在环境和动荷载共同作用下的受压损伤本构模型，并结合MTS试验机测试的受压疲劳试验确定的相关参数，研究了SCC在动荷载、动荷载-水和动荷载-酸溶液共同作用下性能的演变，以期为准确预测CRTSⅢ型板式轨道关键结构材料相关服役性能的变化提供参考。

1 SCC受压疲劳破坏及损伤模型

1.1 SCC受压疲劳损伤本构模型的建立

混凝土是多项复合体系，其内部存在一定的微裂缝等缺陷，疲劳荷载作用将造成微裂缝发展，损伤积累[10-12]。与普通混凝土相比，无砟轨道充填层SCC组成材料复杂，且对原材料质量要求较高，矿物掺和料不低于胶凝材料的30%，具有较高的胶凝材料含量和砂浆含量，新拌阶段的SCC具有高流动度、高抗离析性、较高的均匀性和稳定性等特点，因此与普通混凝土相比，SCC硬化后更加密实均匀，内部的原始缺陷相对较少，对于普通混凝土所具有的疲劳特性同样适用于SCC[13-14]。当高速行驶的列车荷载重复作用在轨道结构上时，充填层将会受到疲劳损伤，且损伤不断积累，此过程也是一个不可逆热力学过程[15]。

由于Helmholtz自由能是一个状态函数[16-17]，具有容量性质，在SCC疲劳损伤的过程中，可以把SCC的Helmholtz自由能ψ表示为损伤度D和应变ε的状态函数，即

ψ=ψ(ε,D)

(1)

基于热力学方程的推导可以得到结合Helmholtz自由能表示的混凝土损伤本构方程的基本公式[17]为

(2)

在混凝土受压疲劳过程中，有相当一部分变形是不可恢复的，这种残余变形也被称为塑性变形，要建立恰当的损伤本构模型，就必须考虑塑性变形的影响，通常可将总应变分写成如下两部分

ε=εe+εp

(3)

式中：εe为弹性应变；εp为塑性应变。

因此，混凝土在疲劳过程中的Helmholtz自由能可以分解为塑性和弹性两部分

ψ(ε,D)=ψe(εe,D)+ψp(εp,D)

(4)

若用C(D)代表SCC经过N次疲劳损伤后的卸除荷载后的刚度，则弹性Helmholtz自由能可以定义为

(5)

由于损伤导致了刚度的退化，且损伤不可逆，所以C(D)为损伤变量D的非递增函数，对于初始无损状态C(D)=E0，则

(6)

SCC在N次疲劳后的弹性Helmholtz自由能用损伤变量表示为

(7)

由式(2)可得

(8)

将式(3)和式(7)代入式(8)可得SCC的受压损伤本构模型

σ=(1-D)E0(ε-εp)

(9)

式中：εp为塑性应变，在疲劳荷载作用下即为残余应变εr。

因此SCC的疲劳损伤本构模型为

σ(N)=[1-D(N)]E0[ε(N)-εr(N)]

(10)

式中：σ(N)≤σ0；σ0为初始加载时的应力值；ε(N)为循环荷载作用N次后的峰值应变；εr(N) 为循环荷载作用N次后的残余应变。

1.2 模型参数的确定

式(10)确定了SCC的受压疲劳损伤本构模型，D(N)为考虑SCC受压疲劳过程中弹性模量衰减的弹性模量损伤因子

(11)

式中：E(N)为混凝土循环加载N次后的弹性模量；E0为混凝土的初始弹性模量。

研究表明，混凝土在受压疲劳加载过程中的残余应变εr(N)与最大应变εmax(N)和疲劳加载次数N之间呈现明显的三阶段发展规律[18]，在疲劳过程中，混凝土残余应变和最大应变的比值可以较好地反映其疲劳过程中的损伤特征，故将其比值定义为SCC的残余应变影响因子

(12)

式中：Φ(N)为残余应变影响因子；ε(N)为循环荷载作用N次后的总应变；εr(N)为循环荷载作用N次后的残余应变。

将式(11)和式(12)代入式(10)中，可得

σ(N)=[1-D(N)][1-Φ(N)]E0ε(N)

(13)

式(13)即为基于Helmholtz自由能的SCC疲劳损伤本构模型，此模型全面考虑了SCC在疲劳过程中弹性模量的衰减和残余应变对SCC的影响，物理意义明确，形式简单。

2 试验验证

针对式(13)的SCC疲劳损伤本构模型，本节采用疲劳试验对其进行验证。模型中的弹性模量损伤因子D(N)用疲劳试验中循环加载N次后采集的弹性模量E(N)和SCC的初始弹性模量E0代入式(11)计算得到，残余应变影响因子Φ(N) 用疲劳试验中循环加载N次后采集的残余应变εr(N)和总应变ε(N)代入公式(12)计算得到，再将弹性模量损伤因子D(N) 和残余应变影响因子Φ(N)代入SCC疲劳损伤本构模型，可以得到循环加载N次后SCC的应力状态，进而可以得到模型拟合曲线，再通过静载抗压试验测试SCC疲劳后的应力应变曲线，最后对比分析模型拟合曲线与试验实测曲线。

2.1 试验方法

本文采用试验的方法对上述SCC的疲劳损伤本构模型进行了验证，试验用原材料及配合比如下[19]：

(1)原材料

水泥：P.O 42.5普通硅酸盐水泥；粉煤灰：F类Ⅰ级灰，比表面积为472 m2/kg，烧失量为2.21%；磨细矿渣粉为S95；砂子：Ⅱ区级配合格，细度模数(2)61的普通河砂，表观密度为2.63 g/cm3；石子： 5～10 mm，10～16 mm的两级配碎石，表观密度为2.67 g/cm3；掺入Ⅱ型膨胀剂和SCC专用黏改剂；减水剂：减水率大于30%的聚羧酸高性能减水剂。

(2)配合比

试验用配合比见表1，各种性能及强度测试按照Q/CR 596—2017 《高速铁路CRTSⅢ型板式无砟轨道自密实混凝土》执行[20]，SCC主要性能参数见表2。

表1 SCC配合比 kg/m3

表2 SCC性能参数

按表1配合比成型100 mm×100 mm×300 mm试件一批共12个，待标准养护室养护56 d后，将试件共分为4组，每组三个试件，试验前对各组试件测试了动态力学性能(动态弹性模量和动态剪切模量)，结果显示，动态力学性能几乎相同，表明成型的试件较均匀，离散较小。

第1组为基准组，继续养护3个月后测试其应力应变曲线；第2组为正常状态200万次疲劳组，继续养护3个月后，取出进行200万次疲劳试验；第3组将其在水中浸泡3个月，取出后进行泡水状态下200万次疲劳试验；第4组将试件在pH值为2.5～3.0之间的硝酸溶液中浸泡3个月，取出后进行泡酸状态下200万次疲劳试验；第3～4组试件进行了疲劳试验后测试其应力-应变曲线。

试件的应力-应变曲线测试采用中南大学现代分析测试中心的电液伺服万能试验机Instron1346进行，静载试验加载现场见图2。疲劳试验采用MTS电液伺服万能试验机，动载频率取12 Hz，最大应力水平取0.35，最小应力水平取0.1，疲劳加载现场见图3。残余应变采集装置为DH3818静态电阻应变仪，测试残余应变的应变片型号为BX120-50AA，电阻为120 Ω，在试件相对的两个侧面沿试件纵向粘贴应变片，将应变片与静态电阻应变仪用导线连接构成残余应变采集系统，残余应变采集现场见图4。

疲劳试验测试时，第3组饱水疲劳组用保鲜膜包裹试件从而保证其处于泡水状态，第4组泡酸疲劳组用浸泡过硝酸溶液的无纺布包裹从而保证其处于酸溶液浸泡状态。疲劳过程中，每隔10 万次暂停一次MTS疲劳试验机并保持0.35的应力水平，读取此时疲劳试验机上的纵向应力和应变采集装置上的纵向总应变ε(N)，由此可以计算得到此时SCC试件疲劳循环加载N次后的静弹性模量E(N)，之后再对疲劳试验机卸载，读取此时应变采集装置上的残余应变εr(N)。

图2 静载实验

图3 疲劳实验

图4 残余应变采集

2.2 应力-应变曲线及SCC性能变化

疲劳试验前实测的基准组、疲劳后的正常状态下200 万次疲劳组、疲劳后的泡水+200 万次疲劳组和疲劳后的泡酸+200万次疲劳组实测的应力-应变曲线测试结果见图5。

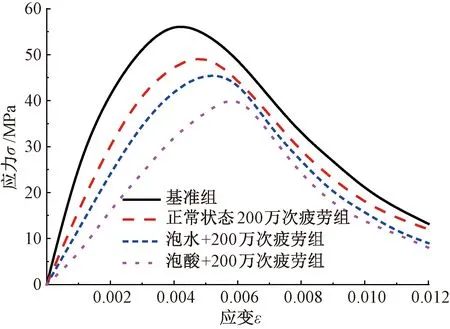
图5 4种不同工况下的应力-应变曲线

由图5可知，疲劳试验后各组试件的应力应变曲线出现了一定的变化。具体表现为，相比较疲劳前的基准组抗压强度而言，正常状态下200 万次疲劳后SCC的强度下降6.97%，峰值应变增大了7.52%；泡水+200 万次疲劳后强度下降11.19%，峰值应变增大了9.97%；泡酸+200万次疲劳后强度下降25.20%，峰值应变增大了13.51%。泡水状态较干燥状态强度下降4.22%，泡酸状态较干燥状态强度下降18.23%。

疲劳过程中的静弹性模量E(N)随疲劳加载次数N的变化见图6，由图6可知，随疲劳加载次数增加，各组混凝土的静弹性模量逐渐降低，特别是在疲劳试验50万次以内时，静弹性模量显著降低。较未受疲劳荷载的SCC，应力水平为0.35的疲劳荷载作用200万次后，动荷载、水+动荷载以及酸溶液+动荷载三种工况下，静弹性模量分别降低了38.3%、40.8%和42.5%。

疲劳过程中的残余应变εr(N)随疲劳加载次数N的变化见图7，由图7可知，随疲劳试验次数的增加，各组试件残余变形逐渐增大，特别当疲劳试验50万次以内时，各组试件的残余变形显著增大。

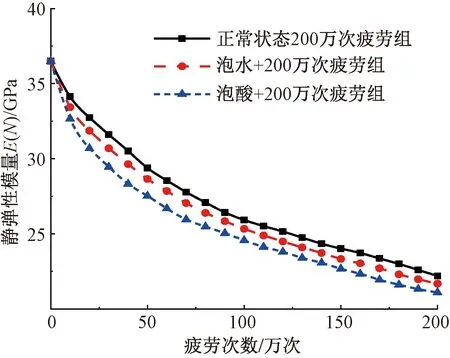
图6 静弹性模量发展曲线

图7 残余应变发展曲线

2.3 模型验证

将试验实测的静弹性模量E(N)和初始弹性模量E0代入公式(11)，可以得到疲劳过程中SCC的弹性模量损伤因子D(N) 随疲劳次数N的关系，见图8。将试验实测的残余应变εr(N)和总应变ε(N)代入公式(12)可得其残余应变影响因子Φ(N)与疲劳加载次数N的关系，见图9。

图8 弹性模量损伤因子演化曲线

图9 残余应变影响因子演化曲线

图10 本构模型拟合曲线与实测曲线对比

将图8和图9中三种工况下的计算结果代入公式(13)，计算可得三种工况下SCC疲劳损伤本构模型的拟合曲线，将三种工况下的拟合结果与实测的应力应变曲线进行对比，见图10。由图10可知，采用本方法SCC的模型拟合曲线与疲劳后的试验实测曲线的相关系数均不小于0.97，这说明采用Helmholtz自由能推导的混凝土本构方程与弹性模量损伤因子和残余应变影响因子相结合构建的充填层SCC疲劳损伤本构模型均能够较好地反映此三种工况下的疲劳损伤情况，本构模型与试验实测数据吻合度较好。在疲劳荷载下SCC的损伤逐渐增大，饱水状态或者酸侵蚀状态将会进一步增大SCC的疲劳损伤。

3 结论

(1)基于Helmholtz自由能构建的SCC疲劳损伤本构方程其物理意义明确，形式简单，结合弹性模量损伤因子和残余应变影响因子，能够较准确地反映充填层SCC在疲劳过程中的损伤演变过程。

(2)在本文的三种工况下，疲劳损伤本构模型的拟合结果与实测结果的相关系数均不小于0.97，说明了该本构模型可以较好地表示复杂环境下SCC的损伤随疲劳次数增加的变化。

(3)相比较未受疲劳荷载的SCC，应力水平为0.35的疲劳荷载作用200万次后，动荷载、水+动荷载以及酸溶液+动荷载三种工况下，SCC极限抗压强度分别降低6.97%、11.19%和25.21%，峰值应变分别增大7.52%、9.97%和13.51%；静弹性模量分别降低了38.3%、40.8%和42.5%。

(4)同时考虑充填层SCC在实际服役过程中的情况和本文的试验结果，发现疲劳荷载作用将导致充填层SCC的损伤逐渐增大，饱水或者酸溶液侵蚀条件将会进一步增大SCC的疲劳损伤。