基于试验统计能量分析的高速列车车内噪声预测方法

张 捷，姚 丹，王瑞乾，肖新标

(1. 四川大学 高分子材料工程国家重点实验室 /高分子研究所，四川 成都 610065；2. 西南交通大学 牵引动力国家重点实验室，四川 成都 610031；3. 常州大学 城市轨道交通学院，江苏 常州 213164)

高速列车的车内噪声直接影响司乘人员的乘坐舒适性，是关乎高速铁路绿色环保和可持续发展的关键问题[1-3]，也是支撑国家“一带一路”建设和“高铁走出去”战略的重要指标。研究高速列车的车内噪声问题，主要的手段是仿真预测或试验分析。其中，仿真预测无论是在车辆设计制造初期，还是运营维护阶段，都能起到积极的指导作用。因此，掌握高速列车车内噪声的预测方法，对于其低噪声设计[4-5]和减振降噪优化具有重要意义。

有关轨道交通的车内噪声预测，国内外已有不少的研究成果可供参考。其中，基于统计能量分析(Statistical Energy Analysis，SEA)[6]的车内噪声预测是较为主流的方法。这是因为高速列车车体结构复杂，具有很强的参数不确定性，传统的数值方法(例如有限元方法)无论是在建模还是计算上都存在困难。Hardy[7]基于SEA方法研究了160 km/h列车的车内噪声特性，分析了空气传声贡献并提出了相应的控制措施建议。Forssén等[8]同样基于SEA方法建立了列车车内噪声预测模型，并用声线追踪法和比例模型试验对车内噪声预测结果进行了验证，发现三者的结果在中心频率500～4 000 Hz的倍频带吻合较好。Fiedler等[9]运用SEA方法研究了不同声源对轻轨列车车内噪声的贡献排序。在国内，谢素明等[10]基于SEA方法建立了某客车卧铺车厢的车内噪声预测模型，通过施加轮轨噪声激励对车内噪声进行了预测，发现预测结果和该车的试验结果在500～2 500 Hz频率范围吻合较好。毛杰等[11]使用SEA方法建立了高速列车的车内噪声预测模型，采用多物理场耦合激励，预测了200～1 600 Hz的车内噪声。Zheng等[12]在SEA方法基础上提出了统计声学能量流方法，考虑车外至车内的声能流动，预测车内的声学响应。Zhao等[13]基于混合有限元-统计能量分析法(Finite Element-Statistical Energy Analysis，FE-SEA)，以及将车体铝型材等效为层合板的方式，建立了高速列车的车内噪声预测模型，发现预测结果和该车的试验结果在100～1 000 Hz频率范围吻合较好。罗文俊等[14]运用FE-SEA方法研究了高速列车的二系悬挂力引起的车体结构振动响应，并分析了车体组成部件对车内结构噪声的贡献。

不难看出，SEA及其相关性方法是高速列车等轨道交通噪声预测的主要手段。但同时也可以发现，在运用SEA时，不同的建模过程和参数设置在计算结果的精度上存在明显差异。怎样合理使用SEA方法进行高速列车的车内噪声建模，特别是如何获得准确的SEA参数，包括结构子系统和声腔子系统的模态密度(Modal Density)、阻尼损耗因子(Damping Loss Factor，DLF)；结构子系统与结构子系统，结构子系统与声腔子系统，声腔子系统与声腔子系统之间的耦合损耗因子(Coupling Loss Factor，CLF)；以及各个子系统的功率输入(Power Input)等，还缺乏系统而深入的研究。本文在现有研究基础上提出一种基于试验统计能量分析(Experimental Statistical Energy Analysis，ESEA)的高速列车车内噪声预测方法，并对上述问题进行详细阐述。

1 统计能量分析基本原理

SEA是大型结构设计初期最常用的计算方法和分析手段。它将复杂结构划分为若干子系统，并将子系统的模态参数处理成随机变量，进而计算分析各个子系统在统计意义上的平均响应。SEA虽然不能针对特定场点给出精确解，但是却可以为设计初期较快地预测大型复杂结构的振动噪声提供参考，在很大程度上和传统数值方法形成互补。

SEA的基本思想是使用功率流平衡方程描述各个子系统之间的耦合关系。对于包含N个子系统的复杂动力学系统，其功率流平衡方程为

ωLE=P

(1)

式中：ω为角频率；E为子系统能量矩阵；P为系统功率输入矩阵；L为包含DLF和CLF的系统能量损耗矩阵。分别为

E=[E1,E2,E3，…，EN]T

(2)

P=[P1,P2,P3，…，PN]T

(3)

(4)

其中：ηii表示子系统i的DLF；ηij表示能量从子系统i传至子系统j的CLF。

SEA的互易性原理为

niηij=njηji

(5)

式中：ni、nj分别为子系统i、j的模态密度。

因此，使用SEA方法对复杂结构进行振动噪声预测分析的关键参数即为模态密度、阻尼损耗因子、耦合损耗因子和功率输入。

2 子系统的模态密度

考虑高速列车的车外声源、车体传声路径和车内声学响应，车内噪声的SEA建模需要划分若干结构子系统(车体)和声腔子系统(车外和车内)。

2.1 结构子系统

高速列车车体结构子系统的划分可以首先按照区域分为地板、侧墙、顶板、端墙、车门、车窗、贯通道等，然后根据每个区域的组成特性再进一步分为诸如铝型材、防寒材、内饰等详细部件。考虑车内噪声SEA模型中子系统划分的几何尺寸，以1 m2样件的测试分析为例，地板铝型材的模态密度测试照片见图1。模态密度通过结构的频响特性分析，使用模态计数法[6]获得。

图1 地板铝型材的模态密度测试

如图1所示，首先将样件用弹性绳进行自由悬挂，然后在样件的一侧随机布置10个加速度计，接着在样件的另一侧使用激振器进行激振。激振器输出的为白噪声谱，上限频率5 000 Hz。

以1 000 Hz以内的频响函数为例，10个加速度计的测试结果见图2。

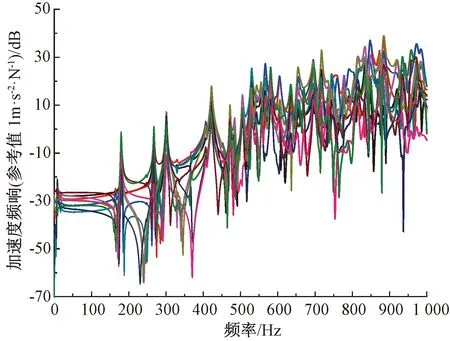
图2 地板铝型材的加速度频响特性

由图2可见，在500 Hz以下，地板铝型材的加速度频响函数峰值较少，以结构的整体模态为主；在500 Hz以上，峰值密集，结构开始出现局部模态。通过将各频带的模态数进行统计，即使用模态计数法可以获得测试样件的模态密度。

地板铝型材、侧墙铝型材、顶板铝型材以及内饰玻璃钢板的模态密度结果见图3。

图3 结构子系统的模态密度结果

由图3可见，结构子系统的模态密度频谱分布上，地板铝型材几乎在全频段都表现得较高，内饰玻璃钢板则基本最低。这一方面说明试验中的铝型材结构相对于玻璃钢板在声振响应上具有更高的被激发能力，另一方面也说明铝型材本身的结构差异是影响其模态密度特性的关键因素。

2.2 声腔子系统

高速列车声腔子系统的划分同样可以按照区域分为车外声腔子系统和车内声腔子系统。对于三维声腔子系统，其模态密度可以表示为[6]

(6)

式中：f为频率；c0为声速；V、S、l分别为三维声腔的体积、表面积、棱边长度。

以车内客室端部区域为例，车内声腔子系统的模态密度计算结果见图4。可以看出，声腔子系统的模态密度随着频率的提高而增加。

图4 客室端部车内声腔子系统的模态密度结果

3 子系统的阻尼损耗因子

3.1 结构子系统

识别结构子系统DLF的方法有很多，半功率带宽法是其中最常用的一种。基于图2的加速度频响特性，就可以使用半功率带宽法获得地板铝型材的DLF。但是，半功率带宽法对于具有密集局部模态的频率(如图2中500 Hz以上的频率)，其阻尼识别将存在困难。因此，对于铝型材500 Hz以上的频率，利用阻尼效应引起的振动随距离的衰减，采用行波法[15]对其DLF进行测试分析。

以地板铝型材为例，基于行波法的结构子系统DLF测试照片见图5。

图5 地板铝型材的DLF测试

基于行波法的地板铝型材DLF测试与图1的区别之处在于激振器和加速度计位于试件的同一侧，并分布在同一水平直线上[16]。相同之处是激振器输出的依然为白噪声谱，上限频率5 000 Hz。

结构子系统的DLF统计结果见图6。其中，铝型材样件在500 Hz以下的DLF基于半功率带宽法，500 Hz以上的DLF基于行波法；内饰玻璃钢板样件的DLF则完全基于半功率带宽法，因为其在分析频率范围内均以整体模态为主。

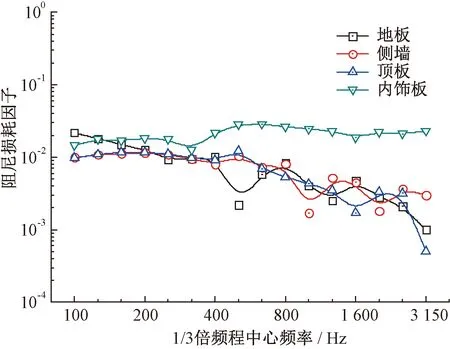
图6 结构子系统的DLF结果

由图6可见，随着频率的提高，铝型材样件的DLF呈现降低趋势，而内饰玻璃钢板样件的DLF则几乎不随频率变化，且明显高于铝型材。

3.2 声腔子系统

声腔子系统的DLF与其混响时间之间存在换算关系，因此，通过测试车内的混响时间，使用混响吸声法可以获得声腔子系统的DLF[6]

(7)

式中：T60为车内声腔的混响时间。

车内声腔的DLF测试照片见图7。

图7 车内声腔的DLF测试

以高速列车车内客室端部为例，关闭车门、内端门，放置2～3 个无指向声源，选择白噪声谱作为输出，上限频率5 000 Hz。在无指向声源附近随机布置5～6 个麦克风，测试车内声腔的混响时间，进而计算得到车内声腔的DLF，见图8。

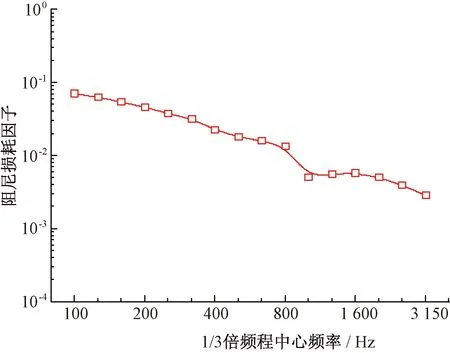
图8 声腔子系统的DLF结果

由图8可见，车内声腔子系统的DLF幅值基本在1%左右，且随着频率的提高而降低。

4 子系统间的耦合损耗因子

4.1 结构与结构子系统

对于高速列车，结构与结构子系统的耦合主要指地板与侧墙、侧墙与顶板等不同类型车体结构子系统之间的耦合。根据SEA基本原理，当结构子系统i和j通过线连接耦合时，其CLF可以表示为[6]

(8)

式中：l为结构子系统i和j的线耦合长度；τij为结构子系统i和j的传递系数；cg为群速度；Si为结构子系统i的面积。

根据式(8)，以地板子系统和侧墙子系统为例，结构与结构子系统之间的CLF结果见图9。

图9 地板与侧墙子系统之间的CLF结果

由图9可见，结构与结构子系统之间的CLF基本随着频率的提高而略有降低。其中，地板子系统与侧墙子系统的CLF相对略高，说明能量流动更容易发生在地板子系统朝向侧墙子系统的方向。

4.2 结构与声腔子系统

对于高速列车，结构与声腔子系统的耦合主要是地板与车内外声腔、侧墙与车内外声腔等车体结构子系统与声腔子系统之间的耦合。以地板与车内声腔的耦合为例，地板子系统(子系统1)传递至车内声腔子系统(子系统2)的功率可以表示为

(9)

此外，基于板件振动声辐射的一般理论，对半无限空间，地板子系统的辐射声功率可以表示为

(10)

式中：σ、S分别为板件的声辐射效率、表面积；ρ、c分别为空气流体的密度、空气中的声速，定义在20 °C时，ρc=415 N·s/m2。

令W12=Wrad，则结构与声腔子系统之间的CLF可以表示为

(11)

因此，通过测试结构的声辐射效率(或辐射声功率)，可以得到结构与声腔子系统之间的CLF。

基于声强扫描法[17]的地板子系统与声腔子系统之间的CLF测试照片见图10。

图10 地板子系统与声腔子系统之间的CLF测试

将地板安装于混响室-半消声室的洞口；在其一侧(半消声室)随机布置10个加速度计，并划分6×6的网格，使用声强探头逐格进行扫描；在其另一侧(混响室)使用激振器进行激振。激振器输出白噪声谱，上限频率5 000 Hz。

基于声强扫描法统计得到的结构与声腔子系统之间的CLF，见图11。

图11 结构与声腔子系统之间的CLF结果

由图11可见，结构与声腔子系统之间的CLF随着频率的提高而略有降低，但是却普遍在中心频率200 Hz的1/3倍频带存在局部峰值，说明该频带振动噪声能量更容易传递。

4.3 声腔与声腔子系统

对于高速列车，声腔与声腔子系统的耦合主要指不同区域的车外声腔子系统和车内声腔子系统之间的耦合。以侧墙区域为例，车外声腔子系统1通过侧墙子系统2与车内声腔子系统3发生耦合，这种耦合称为非接触式间接耦合，见图12。而当2个声腔子系统之间不存在结构子系统而发生直接接触时，这种耦合称为接触式直接耦合。

图12 声腔-结构-声腔 3个子系统相耦合的SEA模型

如图12所示，车外声腔子系统1的能量传递至车内声腔子系统3有2 种路径：一是通过侧墙子系统2的共振模态群(储存能量)传递；二是通过侧墙子系统2的非共振模态群(不储存能量)的质量定律传递。其中，经由侧墙子系统2的共振模态群传递的能量可以通过结构与声腔子系统之间的CLF表征；经由侧墙子系统2的非共振模态群传递的能量，即声腔与声腔子系统之间的CLF(无论是非接触式间接耦合，还是接触式直接耦合)，可以通过下式确定[6]

(12)

式中：c1、V1分别为车外声腔子系统1的声速、体积；S2为侧墙子系统2的表面积；τ13为传递系数。

因此，通过测试结构的声传递系数可以获得声腔与声腔子系统之间的CLF。基于混响隔声法的声腔与声腔子系统之间的CLF测试照片见图13。

图13 声腔与声腔子系统之间的CLF测试

如图13所示，将车体结构样件(包含铝型材、防寒材、内饰板等和实车结构一致的组合样件)安装在混响室-混响室的洞口，根据ISO 140-2[18]等相关标准规定，测试样件的频率隔声量。

混响隔声法统计得到的声腔与声腔子系统之间的CLF见图14。可以看出，声腔与声腔子系统之间的CLF基本随频率的提高而降低。

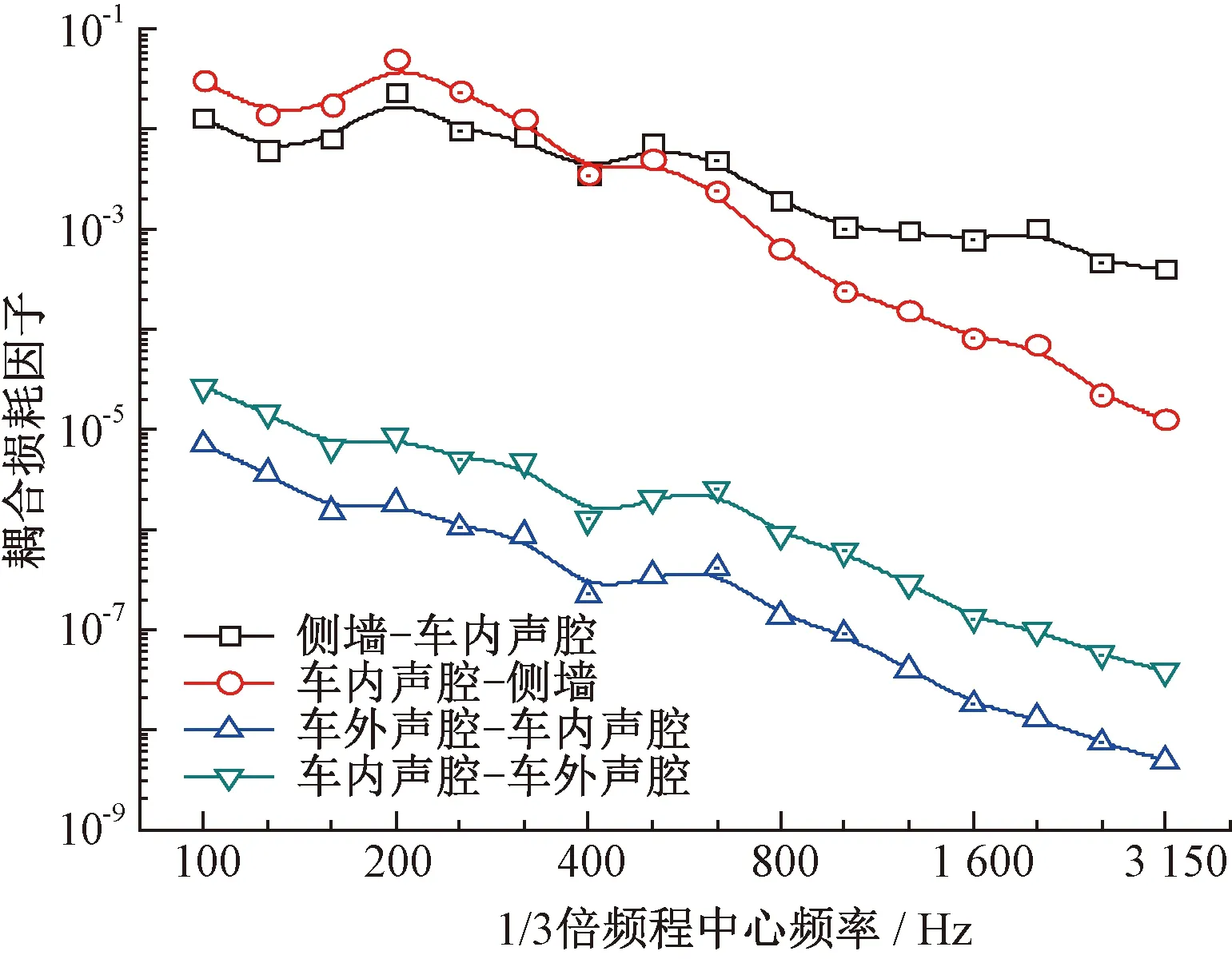
图14 声腔与声腔子系统之间的CLF结果

5 子系统的功率输入

SEA模型子系统的功率输入参数有2种确定方式：一种是通过对噪声源进行仿真分析，计算其噪声和振动频谱；另一种则是采用试验方法获得相关数据。本文采用第二种方式，通过对与建模的高速列车相似的车型进行大量的线路试验数据调研统计，获得其空气声源激励和结构振动激励。

5.1 空气声源激励

以高速列车车内噪声相对较高的受电弓车厢为例，在转向架区域、车身表面区域、受电弓区域和辅助设备区域布置麦克风，测试其噪声特性并进行统计。图15给出了多列、多次试验的统计结果，列车多数处于车轮镟修后5 000 km，即轮轨表面状态良好。测试的列车运行速度为匀速350 km/h。

图15 空气声源激励

5.2 结构振动激励

同样，在车内地板、侧墙、车窗和顶板等位置布置加速度计，测试高速列车的振动特性并进行统计。列车运行速度为匀速350 km/h，测试结果统计值见图16。

图16 结构振动激励

6 车内噪声预测结果与验证

在ESI VA One软件中，考虑高速列车的车体结构特征，以一节受电弓车厢为例，划分车厢子系统并建立车内噪声预测模型。子系统划分过程遵循以下基本原则：

(1)将共振模态参数相似的结构或者声腔划分为一类子系统，例如地板、侧墙或顶板的结构子系统，以及车外或车内的声腔子系统；

(2)综合考虑车辆结构或者声腔的实际几何尺寸与计算精度要求，在满足空间预测位置需要的前提下尽可能使得各个子系统具备高模态数。

高速列车受电弓车厢车内噪声预测SEA模型见图17。

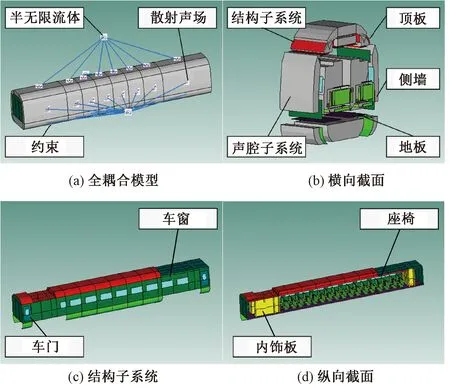
图17 受电弓车厢车内噪声预测SEA模型

高速列车受电弓车厢车内噪声建模时设置了多个车外声腔子系统，在各声腔子系统上输入相应的声压作为激励(5.1节)，模拟空气声源；在各结构子系统上输入相应的加速度作为激励(5.2节)，模拟结构振动。然后使用第2～4节中各个子系统的模态密度、子系统的DLF以及子系统之间的CLF对模型进行赋值，预测车内噪声。其中，车内座椅的建模仅用作车内声腔体积的模拟，其吸声系数用3.2节车内声腔子系统的DLF等效。

高速列车350 km/h运行时，受电弓车厢客室端部车内噪声预测结果和试验对比见图18。

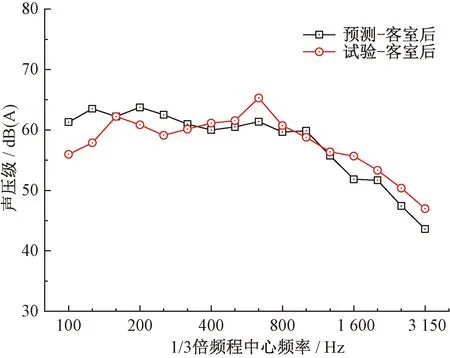
图18 客室端部车内噪声预测结果和试验对比

由图18可见，高速列车车内噪声的预测结果在中心频率100～3 150 Hz的1/3倍频带与试验总体规律吻合较好，峰值频率基本对应。总声压级误差为1 dB(A)左右，符合工程需求且精度较高。

7 结束语

本文提出了一种基于ESEA的高速列车车内噪声预测方法。根据SEA的基本原理，考虑高速列车的车体结构特征，划分了车厢子系统并建立了车内噪声预测模型。通过试验方法研究并获得了高速列车车内噪声预测模型的关键SEA参数。结果表明，车内噪声预测结果和试验在频谱分布上规律一致，总声压级误差在1 dB(A)左右。因此，建模方法和预测模型是可靠、准确的。

但是本文还存在一些问题有待后续进一步深入研究。例如，高速列车的车体几何尺寸庞大，目前的样件尺寸虽然和子系统的划分相接近，但是小样件的测试在较低频率下可能存在应用上的局限和误差。样件尺寸因素的影响有待分析。此外，车体组合结构复杂，铝型材和内饰玻璃钢板之间的连接以及装备状态下的边界条件还欠考虑，这些是进一步准确预测车内噪声传递路径贡献的前提。