城轨列车永磁同步牵引电机全速域转矩闭环矢量控制研究

方晓春，王婷婷，杨中平， 林 飞

(1.北京交通大学 电气工程学院，北京 100044；2. 中车青岛四方车辆研究所有限公司,山东 青岛 266031)

永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)因具有功率密度高、效率高、能够全封闭设计减少维护等优点，在国内外轨道交通牵引领域逐渐被广泛关注[1]。如东芝、西门子、阿尔斯通以及庞巴迪等国外轨道交通装备制造企业已经完成了永磁同步牵引传动系统样机的开发和试验考核，进入了工程化和商业化应用阶段；中国的永磁同步牵引系统研究起步较晚，但已经取得了一些成就，并处于快速发展阶段[2]。永磁同步牵引电机的控制目标为输出转矩，常用的永磁同步电机转矩控制可分为两类，一类是开环控制，另一类是闭环控制。

转矩开环控制也常被称为查表法[3-4]。该方法没有转矩外环，根据转矩指令查表得到电流指令，通过电流环完成转矩输出控制。因其控制逻辑简单，能够保证快速的转矩响应，从而得到了较为广泛的应用。中国的沈阳地铁二号线列车，东芝公司生产的E954/E955系机车等的永磁牵引电机均采用这种转矩控制方式[5]。该方法所用的转矩-电流指令表格基于大量前期实验，缺乏可移植性。且受限于表格数据存储空间与转矩测试点密度，查表法不能保证电流连续变化时的精确转矩控制。

转矩闭环控制的电流内环与转矩开环控制方法基本相同，但其包含一个转矩指令和转矩反馈量以及PI调节器构成的转矩外环。转矩反馈量的计算是转矩闭环控制方法的关键点。根据反馈转矩估算方法的不同，转矩闭环控制主要分为电感辨识公式计算法和定子磁链观测公式计算法2种。电感辨识公式计算法基于永磁同步电机电磁转矩与电流、电感的关系式，其反馈转矩估算的准确性依赖所用电感参数的精确度。电感参数可以在线辨识[6]，但工程可用性与可靠性有待提高；电感参数可以查表得到[7]，但会存在可移植性差、精确度有限的缺点。

永磁同步电机电磁转矩可表示为定子电流与定子磁链的关系式，定子磁链通过观测器得到，其反馈转矩的准确性与所用的定子磁链观测方案密切相关。文献[8]提出了一种永磁同步电机定子磁链和转矩的全阶滑模观测器，并证明采用该方法时电感参数变化对观测的电机电磁转矩精度没有影响；但该观测器较为复杂，不易实现。根据文献[9]提出的扩展磁链模型，文献[10]提出了一种基于扩展磁链模型的最小阶状态观测器，该观测器结构简单，易于实现，且基于拓展磁链观测结果计算的定子磁链不受电机电感参数变化的影响。文献[10]针对风力发电永磁同步电机进行拓展磁链观测研究，其调速范围不宽，因此文中并没有探讨在速度变化范围较大时观测器的极点配置对观测器收敛情况的影响，并且该文献未关注电机启动过程中以及低速段的拓展磁链观测问题。

本文针对城轨列车永磁同步牵引电机全速域转矩闭环矢量控制展开研究。反馈转矩估算主要基于拓展磁链观测，在大转速范围内讨论拓展磁链观测器极点配置，且考虑电机启动与低速段的转矩估算，完成全速域反馈转矩估算。研究高速段逆变器输出电压受限即方波工况时的转矩控制与转速拓展，构建全速域转矩闭环矢量控制方案。该方案在300 kW电机平台进行仿真与实验验证。

1 拓展磁链模型与观测

1.1 永磁同步电机拓展磁链模型

同步参考坐标系下，内置式PMSM稳态电压方程为

(1)

式中：ud、uq、id、iq分别为定子终端电压、定子电流的直轴与交轴分量；Lq，Ld分别为交直轴电感；Rs为定子内阻；ω为电角速度；ψf为永磁体磁链；D为微分算子。将上式进行变换，移除第一个系数矩阵内的Ld，可重新表述为

(2)

式(2)右侧最后一个矩阵被定义为拓展磁链ψe。将式(2)两侧同时进行坐标变换，得到α-β两相静止坐标系下的电压方程

(3)

将式(3)右侧最后一个项转换为关于转子位置θ求导的形式，则式(3)可变化为

(4)

将式(4)右侧最后两项合并，可简化为

(5)

为便于观测器构建，将式(5)表述为

(6)

根据式(6)所示永磁同步电机电压模型，定子磁链与扩展磁链关系为

(7)

根据式(2)可知，扩展磁链是定子磁链在d轴上的一个分量，向量关系见图1。

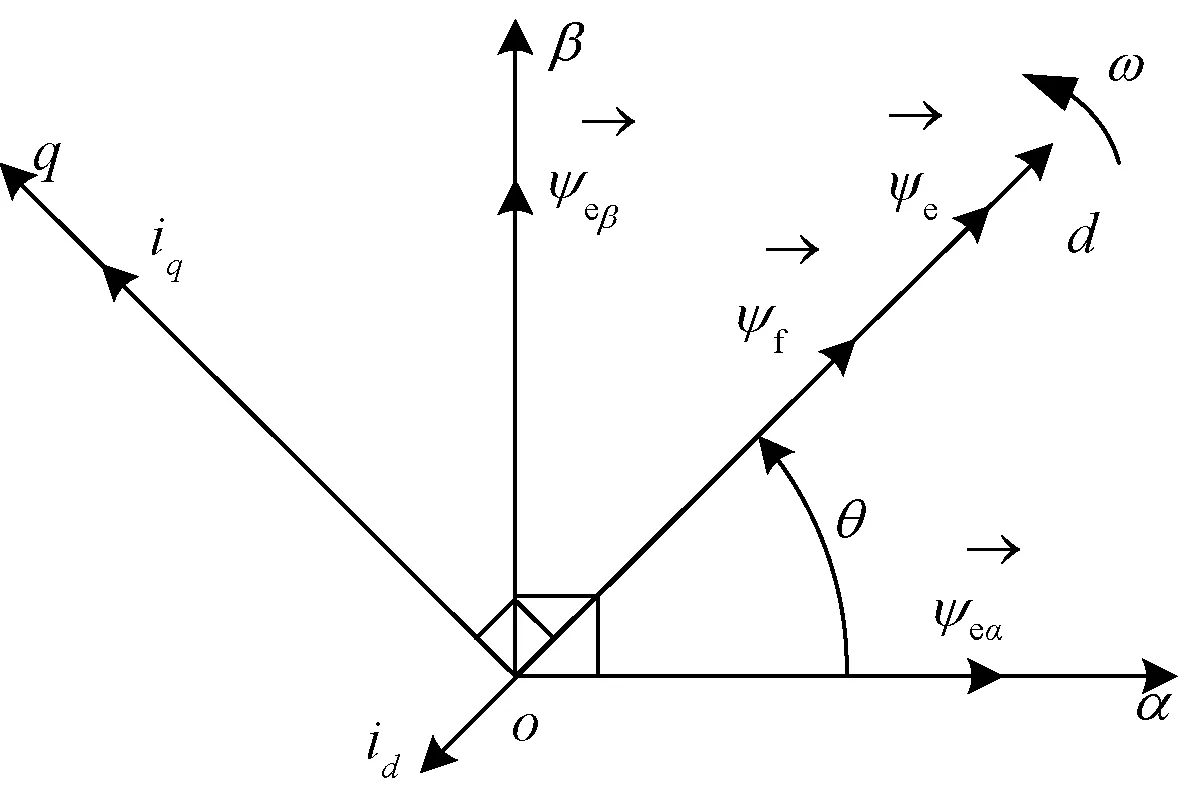
图1 扩展磁链向量图

1.2 最小阶状态观测器

式(6)的第一个等式是进行拓展磁链观测的关键。矢量控制使得电流对其指令信号的跟随响应较快，因而在设计观测器时可忽略拓展磁链幅值ψeαβ的微分，所以拓展磁链的微分可以表示为

(8)

根据式(6)的第一个等式和式(8)的第一个等式，可得拓展磁链状态空间方程

(9)

式中：y为输出向量。

于是可得最小阶扩展磁链状态观测器表达式

(10)

式中：K为反馈增益矩阵。对比式(9)和式(10)，扩展磁链观测器的观测误差为

(11)

式(10)所示拓展磁链观测器公式中存在电流微分项，容易引入噪声。引入式(12)所示中间观测量，消除电流微分项。

(12)

综合上述，PMSM拓展磁链状态观测器设计见图2。

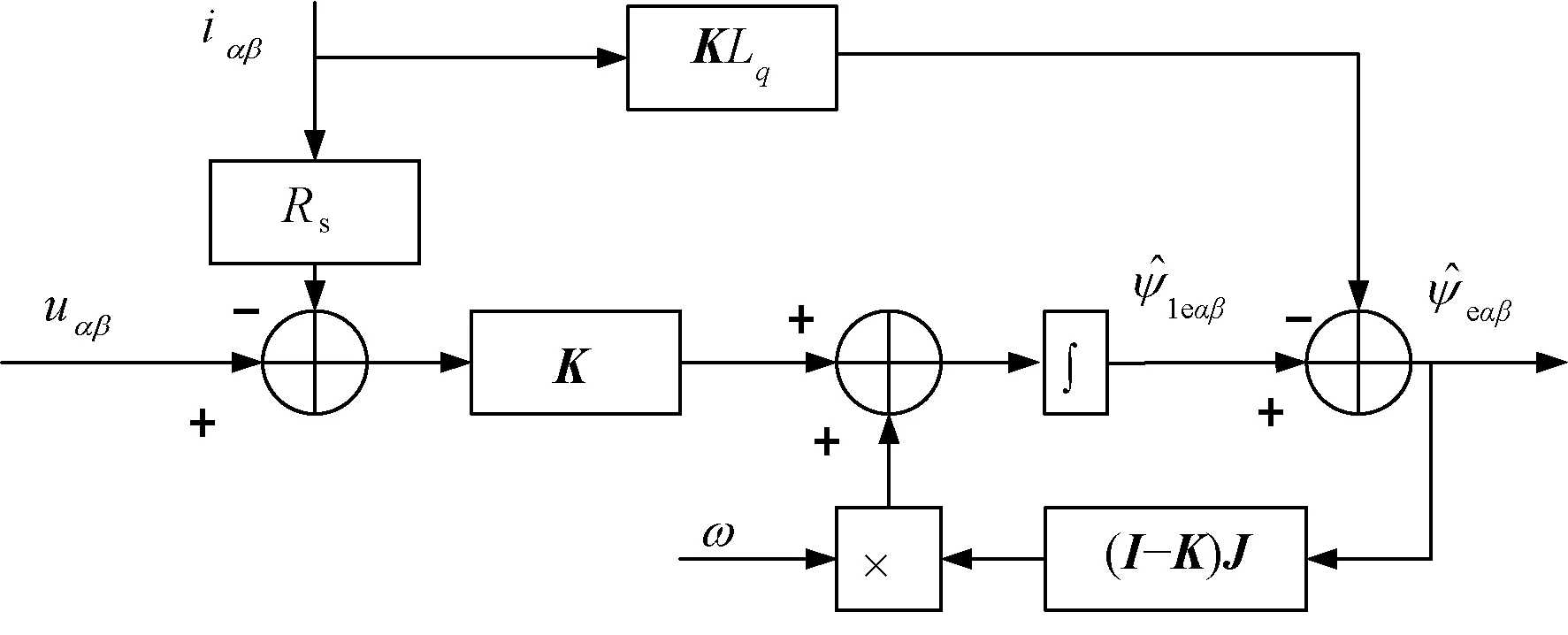
图2 扩展磁链状态观测器

1.3 状态观测器极点配置

观测误差的微分方程见式(11)。则ω(I-K)J的特征值被称为观测器的极点。当观测器的全部极点都具有负实部时，观测误差趋近于0，观测器的输出能够收敛于被观测对象。为使状态观测器能够合理的收敛，需要对观测器的极点进行配置。假设反馈矩阵K为

(13)

将矩阵K带入观测器误差方程(11)并展开

(14)

根据式(14)可知，设定k1=k4=1可以消除α轴和β轴之间磁链观测的耦合，在出现系统扰动时，具有更好的观测性能。从而，反馈矩阵还有2个待定系数k2和k3。此时，观测误差微分方程系数矩阵特征值计算如下

(15)

由式(15)可知，-k2和k3即为状态观测器的极点。为使状态观测器收敛，且α轴和β轴的扩展磁链观测收敛速度相同，令k2=-k3=k，k大于零。将k带入误差微分方程可得

(16)

由式(16)可以看出，ωk越大，误差衰减越快，状态观测器的收敛速度越快。若k取为固定值，那么状态观测器的收敛速度将随转速ω的变化而变化，这对观测是不利的，因此将参数k配置为k′/ω的形式。

当磁链误差值小于等于实际值的3%时，认为观测器收敛。状态观测误差的收敛时间与k′的关系见图3。

图3 状态观测器收敛时间随参数k′的变化关系

取不同数量级的数个收敛时间为代表，其与相应的k′值构成表1。

表1 收敛时间与相应的k′值

在表1所示数据中，k′≤35时收敛时间过长以至于大于0.1 s，因此不予考虑。但是观测误差的收敛速度并非越快越好，观测误差收敛速度快，往往对应输出误差反馈矩阵有较高增益，这将导致观测器对测量噪声的敏感程度增加。为了进一步选取合适的收敛时间，对表1中k′≥35以后的取值进行仿真。q轴扩展磁链发生0.12 Wb阶跃变化，k′分别取值35、70、351、3 510，观测结果分别见图4。

图4 k′不同取值时扩展磁链阶跃变化观测结果

由仿真结果可以看出，k′取值越小，磁链发生阶跃变化时，状态观测量收敛时间越长，但扩展磁链的谐波幅值却相对越小；k′取值越大，状态观测量收敛时间越短，但脉动幅值越大。应选取合适的k′值，使得收敛时间满足控制要求，且脉动幅值相对较小。在列举的仿真结果中，k′取值70至351之间时扩展磁链收敛速度和脉动幅值都在可接受范围内，本文选定k′=100。

1.4 参数鲁棒性分析

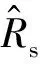
(17)

对式(17)进行转换，可得

(18)

式(18)左侧为基于定子电压模型进行积分计算定子磁链的公式，右侧为本文观测电机实际定子磁链的公式。

(19)

由于式(18)在拓展磁链观测过程中恒成立，从而依据式(19)观测到的定子磁链精确度ψs与PMSM的电感参数无关。

2 全速域转矩闭环方案

2.1 反馈转矩计算

电机输出电磁转矩可表示为电机极对数、定子磁链矢量和定子电流矢量的乘积

(20)

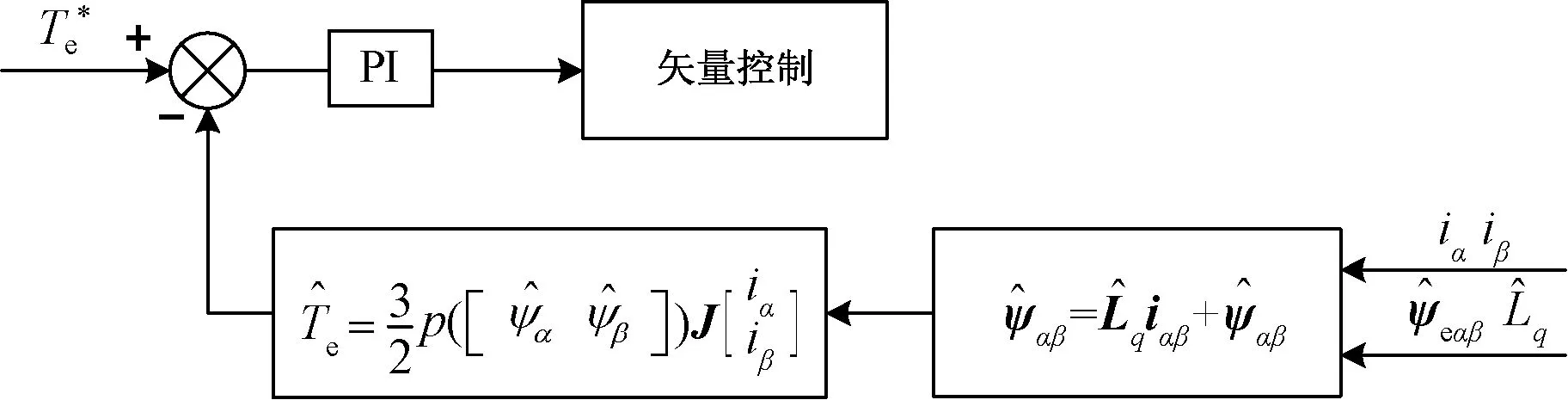
图5 基于磁链观测的转矩闭环控制框图

由式(16)与前文分析可知，本文所用拓展磁链观测器极点配置与电机转速成反比，从而在启动阶段理论极点为无穷大，意味着该观测器不适用于电机启动阶段。因此在电机启动过程中，转速较小及电机反转时，反馈转矩由电流与交直轴电感的关系式得到

(21)

当电机转速大于10 r/min后切换到定子磁链观测转矩计算法，保证电机正常启动。

2.2 转矩闭环方波弱磁控制

牵引传动系统中，逆变器输出电压受限，从而PMSM在高速域需弱磁运行，拓展转速，并输出一定转矩[11]。为最大化输出电压，牵引逆变器在高速域往往采用方波单脉冲调制，此时的电机控制可视为电压严格限制的弱磁控制。方波工况时逆变器输出相电压基波幅值固定为最大值U1max

U1max=2udc/π

(22)

式中:udc为逆变器直流侧电容电压。方波工况下电压基波幅值不再作为电机控制自由度，电压基波相位成为惟一控制自由度。PMSM方波工况弱磁控制可分为三类：一是前馈控制[12]，由于参数依赖性强且动态响应受限而应用不广；二是负直轴电流补偿法改进方案[13]，控制框架复杂而不利于实现；三是电压相角法及其改进方案[14]。电压相角法是针对逆变器方波工况PMSM控制而被提出的，在工程实践中应用较广。通过调节电压基波相位控制电机转矩，直面PMSM方波控制自由度惟一的问题。该方法中的电压相角θv的定义以及与电机输出转矩的关系为

(23)

式中:Us为合成电压矢量幅值，若矢量控制坐标变换原则为等幅值，则方波工况下其最大值Usmax等于U1max。根据式(20)计算反馈转矩，与转矩指令比较得到转矩误差，经PI调节器输出电压相角θv，构建电压相角法弱磁控制，见图6。

图6 电压相角法弱磁原理图

2.3 全速域转矩控制方案

基于拓展磁链观测器计算反馈转矩，电机中低速域采用典型的PMSM双电流闭环控制，高速域采用电压相角法弱磁控制，得到牵引永磁同步电机全速域转矩闭环控制方案见图7。其中，2种控制策略的切换逻辑见图8。

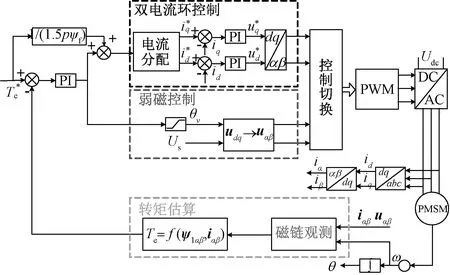
图7 PMSM全速域转矩闭环控制框图

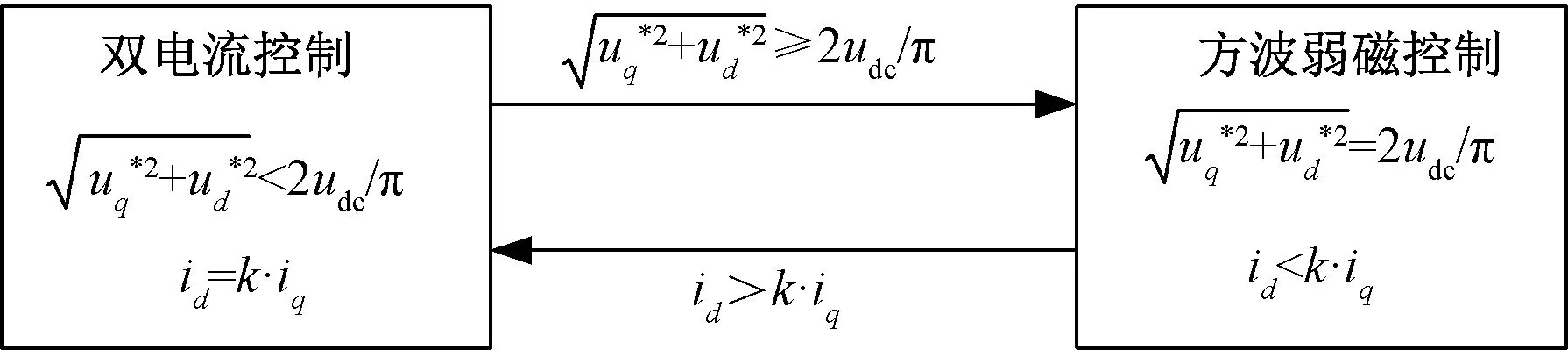
图8 弱磁控制切换判据

如图8所示，双电流环控制时，定子电压指令幅值小于方波工况下的最大电压矢量幅值2udc/π。当电压指令幅值达到2udc/π后，继续增加电机转速或者负载，电机切换为电压相角法弱磁控制。当进入方波工况后，电压矢量幅值被限定为2udc/π，不随工作状态变化，电压指令不能再作为退出弱磁控制的判据。PMSM工作区域分为3个，其中弱磁区在id-iq坐标平面上位于最大转矩电流比(Maximum Torque Per Ampere,MTPA)曲线的左侧[15]。由于电感参数与磁链参数受电机定子电流与温度等因素大范围变化, 可将MTPA曲线近似线性化为id=kiq而便于工程应用，其中k<0。从而id>kiq可作为退出弱磁控制的判据。在进入弱磁控制的第一个控制周期，需对电压相角θv调节器的积分器进行前馈赋值；在退回双电流环控制的第一个控制周期，需对交直轴电流调节器的积分器前馈赋值，避免出现电压指令突变及电流冲击。

3 仿真与实验

基于300 kW永磁同步电机对拖平台，对基于拓展磁链观测的PMSM转矩闭环控制方案进行验证。平台硬件系统主要包含1 500 V/750 V直流电源、滤波电抗器、支撑电容、两电平逆变单元、300 kW永磁同步电机、190 kW异步电机以及其他构成部分。其中永磁同步电机作为牵引电机运行，是本文主要控制对象；异步电机作为负载电机，采用VVVF开环控制。平台实物见图9，PMSM部分参数见表2。

图9 300 kW永磁同步电机对拖实验平台

表2 PMSM 实验平台参数

3.1 仿真

采用表2所示电机参数搭建Matlab/Simulink仿真模型。为模拟对拖平台，永磁同步电机的机械负载输入量为转速。采用图7所示的全速域转矩闭环控制方案，进行加速仿真，结果见图10。永磁同步电机转速每秒增加1 000 r/min，2 s后至2 000 r/min保持不变。永磁同步电机转矩指令在启动后的0.1 s内从0增加至400 Nm，之后保持恒定。

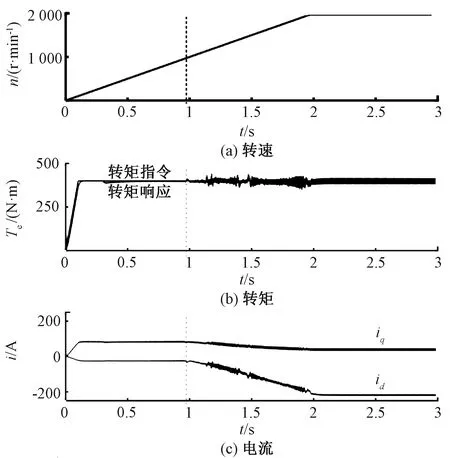
图10 转矩闭环控制下加速仿真结果

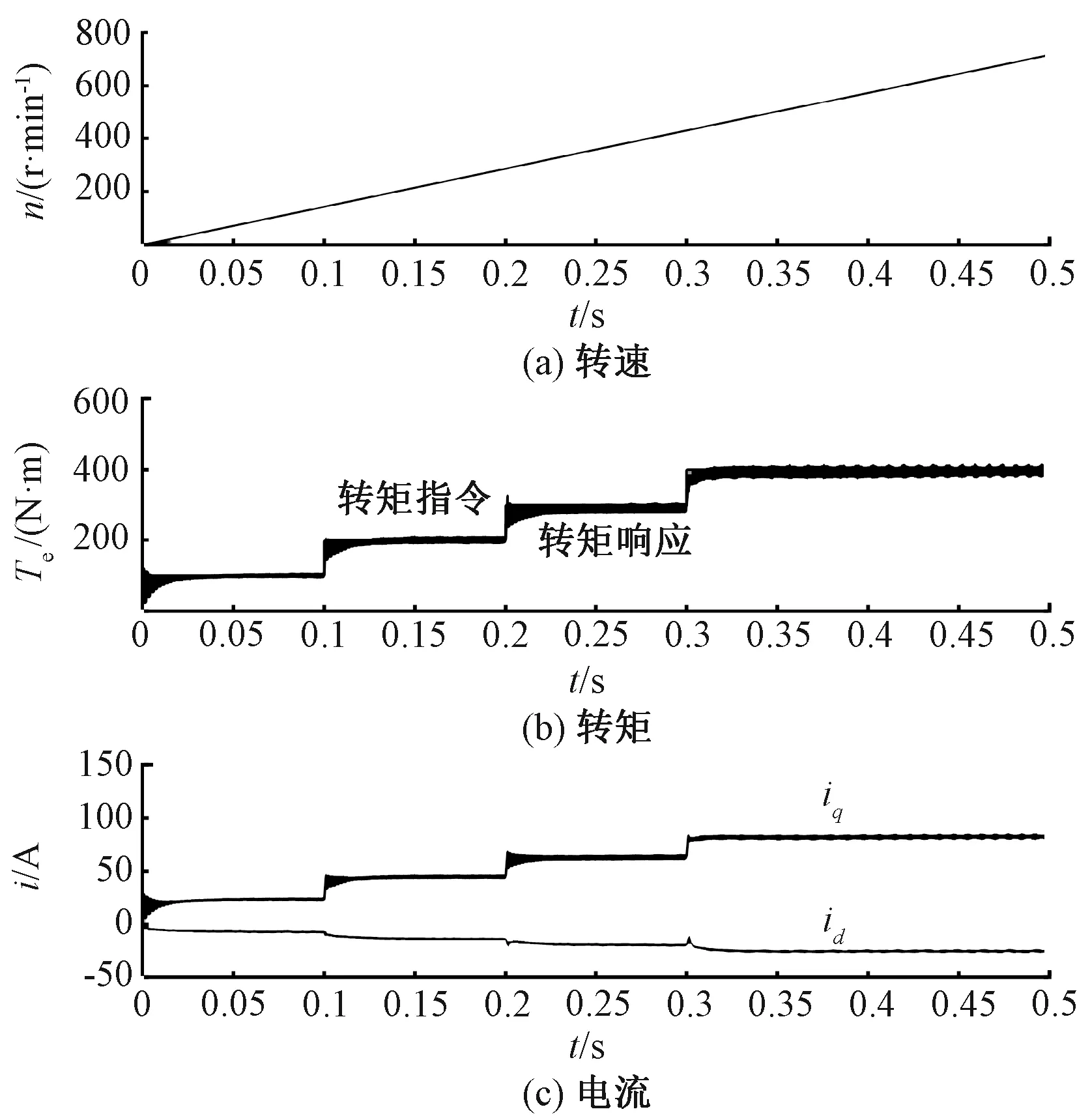
图11 转矩闭环控制恒转矩区转矩阶跃仿真结果

电机转速n<960 r/min时，电机采用双电流环控制；图10所示电机的输出转矩能够很好的跟随转矩指令，保持400 N·m不变。当电机转速n>960 r/min时，定子电压幅值逐渐饱和，电机开始进入弱磁控制；转矩外环通过调节电压相角使电机的转矩仍然能够跟踪上转矩指令，保持400 N·m不变；电机的直轴电流id逐渐减小，产生去磁作用，完成弱磁拓速。

图11所示为恒转矩区转矩指令阶跃工况下的转矩、电流仿真结果。仿真过程中，负载的转速均匀变化，转矩指令从初始100 N·m开始，每隔0.1 s发生100 N·m的阶跃变化。仿真结果表明，电机转矩和电流响应迅速，动态控制性能良好。

仿真结果验证了本文所提出的基于定子磁链观测的全速域转矩闭环控制方案。

3.2 实验

图12所示为转矩闭环加速实验结果。该实验中平台转速由负载电机控制从300 r/min逐渐增大至1 900 r/min。永磁同步电机转矩指令给定为400 N·m。在转速为900 r/min左右时，PMSM由双电流环控制切换进入弱磁控制，交直轴电流逐渐减小。图12实验结果表明，无论是双电流环控制还是电压相角法弱磁控制，电机转矩对转矩指令都有较好的跟随性能。电机反馈计算转矩在398 N·m到415 N·m之间波动，其平均值与转矩指令以及转矩仪显示的转矩基本一致。整个速度域的转矩脉动较小，转矩控制精度较高。

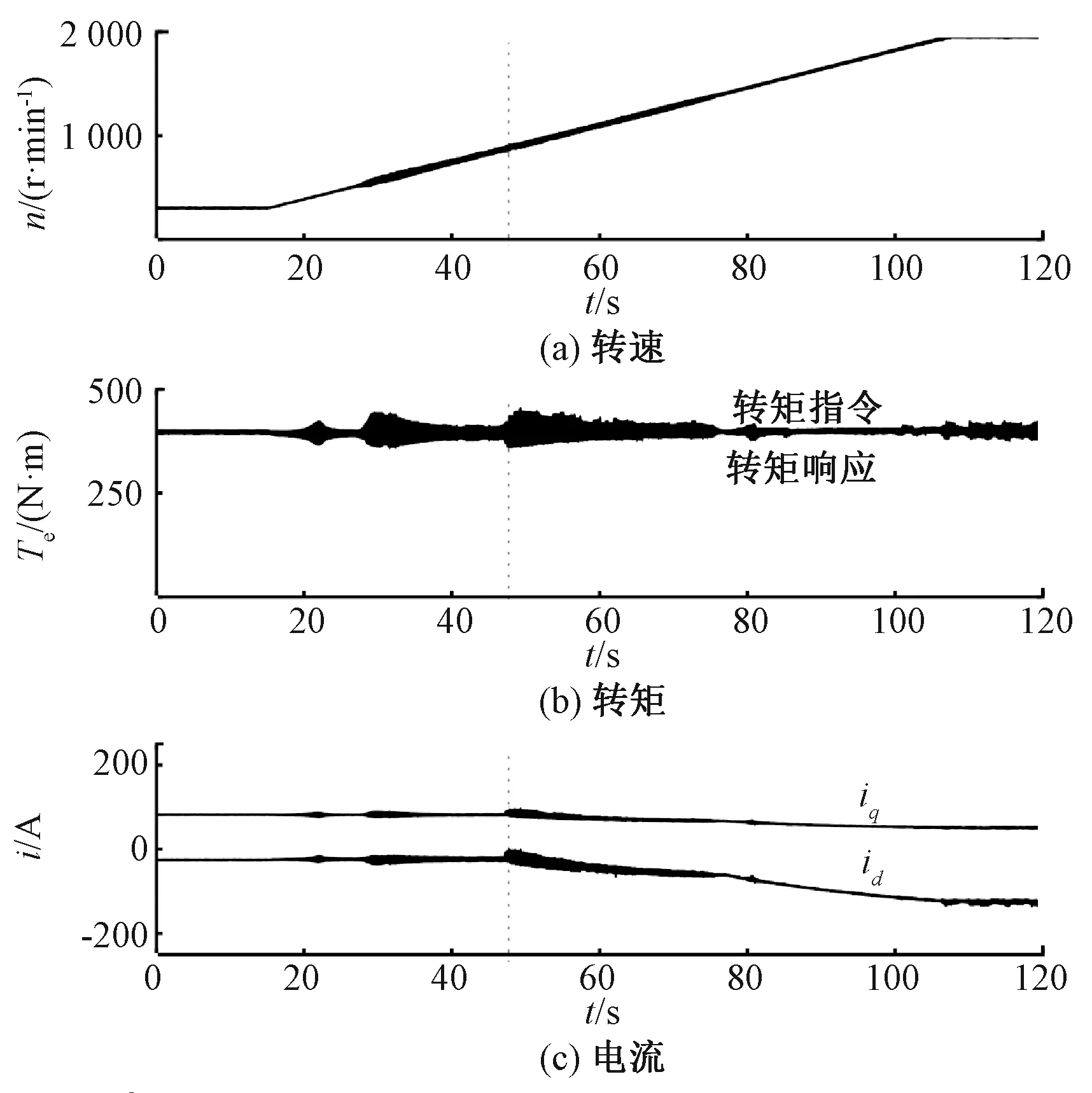
图12 转矩闭环控制下加速实验结果

图13所示为恒转矩区转矩阶跃实验结果。转矩指令由100 N·m开始以50 N·m的幅度逐渐阶跃到450 N·m。电机转速保持300 r/min不变。在转矩指令发生阶跃变化时，电机的转矩能够跟随转矩指令的变化。

图13 恒转矩区转矩阶跃实验

实验结果同样验证了本文所提出的基于定子磁链观测的全速域转矩闭环控制方案。

4 结论

针对常用PMSM转矩控制方案缺点，本文采用基于定子磁链观测的反馈转矩估算方法，以克服电感参数变化对转矩控制的影响，提升转矩控制精度。搭建了扩展磁链最小阶状态观测器，该方法定子磁链观测精度高，可靠性强，且不受电机电感参数变化的影响。考虑电机调速范围条件下，分析了扩展磁链观测器极点配置方法，根据系统需求对观测器极点进行配置，使观测器能够有合适的收敛速度。

本文提出了基于定子磁链观测的PMSM全速域转矩闭环矢量控制策略。受限于观测器极点配置，反馈转矩的计算在电机启动与低速段采用电感辨识公式计算法，转速较高时过渡到磁链观测公式计算法。永磁同步电机在中低速域采用经典的双电流闭环矢量控制，在高速域采用电压相角法弱磁控制，完成了全速域转矩闭环矢量控制。

本文所提出的城轨列车永磁同步牵引电机全速域转矩闭环矢量控制方案在300 kW永磁同步电机实验平台上得到了验证。其定子磁链观测方法与反馈转矩计算方法适用于其他场合的PMSM控制。牵引传动系统对逆变器直流电压利用率要求很高，从而需要进入方波工况。本文强调的方波弱磁控制，可用于其他直流电压受限条件下的PMSM控制。