基于LSTM网络的铁路货运量预测

程肇兰，张小强,2,3，梁 越

(1.西南交通大学 交通运输与物流学院，四川 成都 611756；2.综合交通大数据应用技术国家工程实验室，四川 成都 611756；3.综合交通运输智能化国家地方联合工程实验室，四川 成都 611756)

铁路货物运输长期以来扮演着国民经济发展中的重要角色，但随着公路、航空等运输网络的逐步完善以及顾客运输需求的变化，铁路货物运输正面临其他运输方式的激烈竞争。铁路运输企业需要制定灵活的运输计划和营销策略以改善铁路货物运输的局面，这就需要铁路运输部门准确预测并掌握计划期内的货运量。目前对铁路货运量预测的研究主要侧重于年度货运量预测，但短期货运量(月、日货运量)作为月度货物运输计划和旬日历装车计划、车站货运日班计划、空车运用计划等日常工作计划编制的依据，其准确预测在铁路日常工作组织层面也有十分重要的意义。因此，如何提高铁路短期货运量预测精度已然成为铁路运输企业亟待解决的问题[1]。铁路货运量因受到宏观经济因素、竞争因素、运输货物本身季节特性等影响而呈现上下浮动和季节波动特性。宏观经济因素与竞争因素对货运量的影响存在滞后效应，这种滞后效应表现为前一段时间的经济情况、竞争情况影响后一段时间运输企业采取的经营策略和货主对运输方式的选择，进而影响铁路货运量。多元回归预测、支持向量机、BP(Back Propagation)神经网络等预测方法[2-5]因在进行铁路短期货运量预测时没有考虑到这种延迟和滞后效应，所以预测精度有限。长短期记忆网络(Long Short-term Memory, LSTM)特别适合处理和预测间隔和延迟相对较长的时间序列，已经广泛应用于股票、短时交通流、疾病、点击率等方面的预测，但在铁路短期货运量预测方面的应用较少。本文借助LSTM网络模型研究铁路短期货运量预测。

1 LSTM网络理论

LSTM网络是一种特殊类型的循环神经网络(Recurrent Neural Network，RNN)。

1.1 RNN

拥有输入层-隐含层-输出层结构的传统神经网络如BP神经网络在相邻两层间一般采用全连接方式，但非相邻两层的神经元之间没有连接，同一层内的神经元间也无连接，见图1(a)。RNN由BP神经网络改进而来，与BP神经网络最大的不同之处在于RNN隐含层内的神经元之间存在连接。如图1(b)所示，RNN中隐含层的输入不仅包括输入层的输入还包括上一时刻隐藏层的输出，这意味着RNN网络会记忆前面的信息并应用于当前输出的计算中。因其在记忆方面的能力，RNN网络已经成功应用在语音识别、机器翻译、音乐生成、文本生成等自然语言领域[6]。

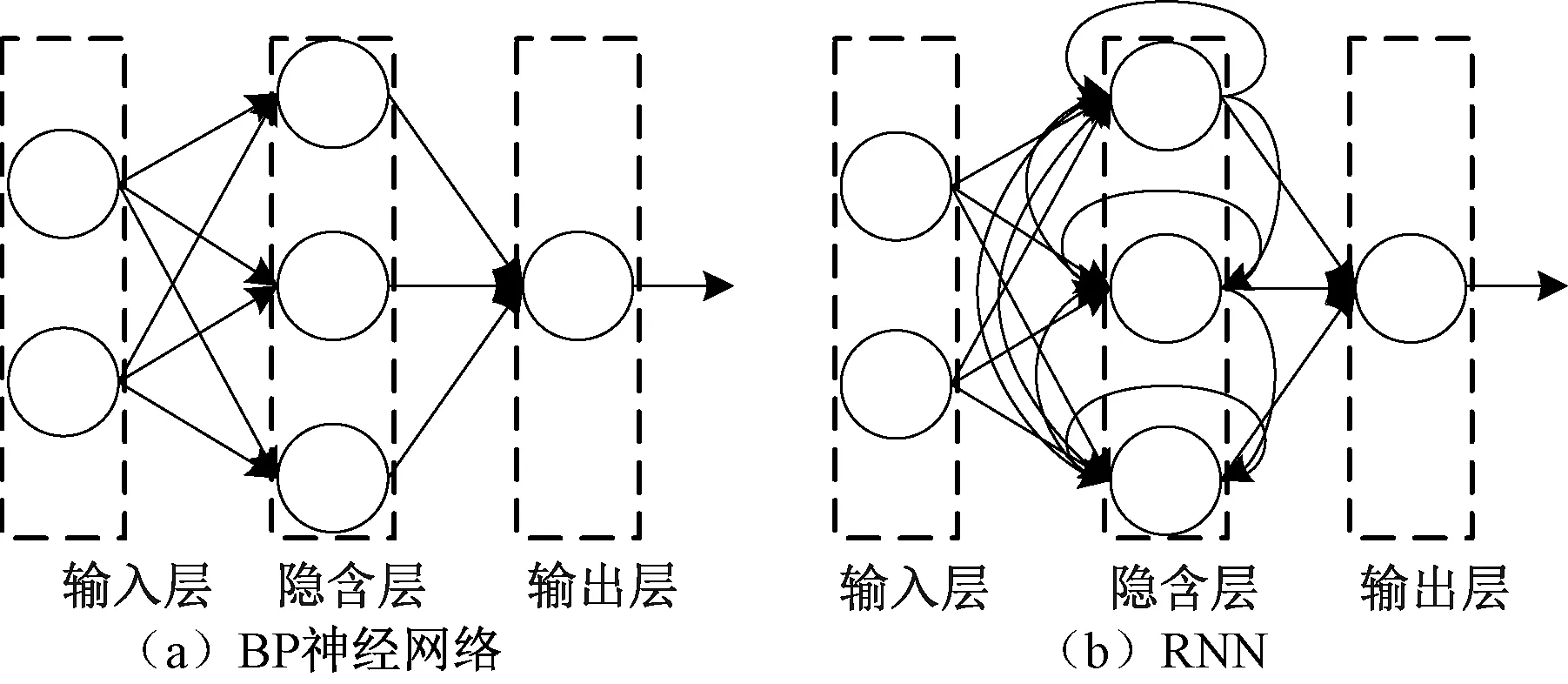
图1 BP神经网络与RNN对比

标准的RNN模型结构见图2。x(t)为t时刻的样本输入；h(t)为t时刻的隐藏状态，由x(t)和t-1时刻的隐藏状态共同决定h(t-1)；O(t)为t时刻模型输出，只由h(t)决定；L(t)为t时刻的损失函数；y(t)则为训练样本时的真实输出；U、W、V为网络共享参数。

图2 标准RNN结构

1.2 LSTM

RNN的两种传统算法——基于时间的反向传播算法(Back-propagation Through Time, BPTT)和实时循环学习算法(Real-time Recurrent Learning，RTRL)，可能会因为出现梯度爆炸或者梯度消失的情况而失效[7]，因此在实际中，标准RNN的应用范围有限，取得更多成果的大多是RNN的改进网络。LSTM网络就是为了避免上述问题而专门设计的一种特殊类型的RNN网络，在1997年由Sepp Hochreiter和Jürgen Schmidhuber第一次提出。LSTM的巧妙之处在于通过增加输入门、遗忘门、输出门以获得变化的自循环权重，在模型参数固定的情况下，不同时刻的积分尺度得以动态改变，从而能够规避梯度消失或者梯度爆炸的问题[8]。

f(t)=σ(Wf·[h(t-1),x(t)]+bf)

(1)

i(t)=σ(Wi·[h(t-1),x(t)]+bi)

(2)

(3)

(4)

o(t)=σ(Wo·[h(t-1),x(t)]+bo)

(5)

h(t)=o(t)·tanhC(t)

(6)

式中：f(t)为t时刻遗忘门的输出；i(t)为t时刻输入门的输出；o(t)为t时刻输出门的输出；Wf、Wi、Wc、Wo和bf、bi、bc、bo分别为遗忘门、输入门、细胞状态、输出门对应的系数；σ为sigmoid激活函数；tanh为双曲正切激活函数。

图3 LSTM的隐藏层结构

2 LSTM货运量预测模型构建

铁路货运量受许多因素影响。在现实中，影响因素值的统计最短周期往往较长，一般以月或更长的时间段进行统计。日货运量的影响因素值往往因为周期太短而无法获取。因此，对于不同时期(月、日)的货运量预测，应当依据不同时期的特点，分别建立LSTM货运量预测模型。针对月货运量预测，建立基于月货运量数据的LSTM多变量预测模型；针对日货运量预测，建立基于日货运量数据的LSTM时间序列预测模型。

2.1 模型输入

对于基于月货运量数据的LSTM多变量预测模型，由于宏观经济因素、竞争因素对货运量的影响存在滞后效应，因此t时刻的货运量yt不仅受到t时刻影响因素Xt的影响，还同时受到t-1,t-2,…,t-k(k=1,2,3,…)时刻影响因素Xt-1,Xt-2,…,Xt-k的影响。且影响因素Xt-k的影响力随k递增而减弱。假设t月的货运量yt将同时受到t-1,t-2,…,t-k月影响因素的影响，忽略t-k月之前的影响因素的影响力。又考虑到t月不能观察到在t+1月公布的t影响因素值。因此，基于月货运量数据的LSTM预测模型t时刻的输入是t-1,t-2,…,t-k月影响因素值Xt-1,Xt-2,…,Xt-k及对应的月货运量yt-1,yt-2,…,yt-k。

对于基于日货运量数据的LSTM时间序列模型，考虑难以准确获取影响因素每日统计值，模型t时刻的输入为t-1,t-2,…,t-k时刻的日货运量yt-1,yt-2,…,yt-k。

2.2 模型结构

两个模型的基本结构均为输入层、隐含层和输出层的神经网络结构。隐含层均采用多层LSTM单元。可以通过网格搜索[10]方法确定合适的隐含层数、合适的神经元个数超参数取值。本文采用的损失函数为均方差(Mean Squared Error, MSE)[11]，计算方法为

(7)

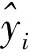
2.3 模型评估

为评估模型预测效果，采用均方根误差RMSE、平均绝对值误差MAE和R2平均绝对百分比误差MAPE[12]。

各误差计算方法如下所示：

(8)

(9)

(10)

(11)

3 实证案例

3.1 试验数据

本文的研究数据来自于中国铁路广州局集团有限公司(以下简称广铁集团)2009—2017年的原始货票数据记录。在对货票数据进行去除废票、删除缺失值、去除不合理数据等数据清洗后，统计得到广铁集团2009—2017年每日和每月的货运发送量，见图4。总体上，两者的随机变动与周期性变动趋势均比较明显且保持大体一致：前者主要在5 000车上下波动，而后者在160 000车上下波动； 前者与后者均在每年2月份到达波谷，随后上升并持续在小范围内波动。

图4 广铁集团2009—2017年货运发送量

3.2 铁路货运量影响因素指标选取及相关性分析

一个地区的铁路货运量通常受到各个方面因素的影响，主要包括地区的宏观经济运行情况、市场供需结构、外部竞争环境等外部因素和铁路营业里程、运输能力、服务水平等内部因素。在外部因素中，表示宏观经济运行状况的地区生产总值对铁路货运量大小起决定性作用。又考虑到铁路货物运输的对象主要涉及国民经济重要组成部分中的第一产业和第二产业产品，第一产业总产值和第二产业增加值也能够直接体现第一产业和第二产业的经济运行情况。由于铁路货物运输的特点和性质，其主要受到来自公路货物运输的竞争，因此选取公路货运量表示对铁路运输竞争力的大小。在内部因素中，铁路营业里程的增加特别是高速铁路的大量投入运营，能释放平行的既有线运输能力并提高运行图中货运列车铺画密度，进而提升货物运输能力[13]。表1为2009—2017年原广州铁路局范围(广东省、湖南省、海南省)内的部分月份影响因素取值[14]。

分析上述影响因素之间相关性和各影响因素对广铁集团月货运量的影响大小，各影响因素之间、各影响因素与月总货运量的相关性系数图，见图5。

图5 广铁集团2009—2017货运量(单位：车)

图5中，对角线部分代表各影响因素和月货运量自身分布，下三角部分画出了对应的散点图，上三角部分则代表对应的相关系数，星星越多表示两者的相关性越强。由图5可知，上述影响因素(不包括GDP)与铁路月货运量均存在较强的相关性，且第一产业总产值和公路货运量与铁路月货运量的相关性尤为突出。但GDP与铁路月货运量的相关性不显著，这可能是因为以季度平均GDP代替每月实际GDP，不能体现GDP在季度内的变化趋势。在影响因素之间，GDP、第二产业增加值、第一产业总产值、铁路运营里程之间均存在很强的相关性。结合指标数据获取情况和以上分析，确定以下因素为铁路货运量影响因素的指标：第二产业增加值、第一产业总产值、铁路运营里程、公路货运量。

3.3 参数设置及试验结果

(1)基于月货运量数据的LSTM多变量预测模型及参数选择

网络构建采用Keras框架实现LSTM[16]，将数据集分为训练集(前8年数据)和测试集(后1年数据)。通过反复试验发现，k=1且采用单层隐含层的LSTM网络具有最好的预测精度，包含的节点数为6。模型采用Adam(Adaptive Moment Estimation)优化算法[17]，激活函数采用tanh函数。

(2)基于日货运量数据的LSTM时间序列预测模型及参数选择

模型将数据集的前70%作为训练集，后30%作为测试集。通过反复试验，确定时间步长k=1时，采用单层隐含层的LSTM网络模型的预测精度最高，每层包含的节点数为5。优化算法亦采用Adam，激活函数采用tanh函数。

(3)试验结果

表2为预测结果的评价指标。

表1 部分月份影响因素取值

由表2可知，基于月货运量数据的LSTM多变量预测模型的预测结果显示，测试集上16万车左右的货运量的预测平均绝对值误差在8 574车，平均绝对值百分比误差为6.0%。基于日货运量数据的LSTM时间序列预测模型的预测结果显示，测试集上5 200车左右的货运量的预测平均绝对值误差在348车，平均绝对值百分比误差在7.9%左右。两者的预测精度均较高。

3.4 对比试验

为比较LSTM预测方法与其他预测方法的预测精度，本文采用另外两种比较常用预测方法-时间序列预测模型[18]和BP神经网络预测[19]。类似地，对月货运量时间序列数据建立ARIMA(0,1,1)(0,1,2)[12]模型，模型为

(1-B)(1-B)Yt=(1+0.507 8B)

(1+0.915 7B12-0.246 6B24)εt

(11)

式中：Yt为时间序列；B为延迟算子；εt为白噪声随机误差序列。

对日货运量数据的时间序列数据建立ARIMA(1,1,1)，模型为

Yt=0.262 6Yt-1+εt-0.705εt-1

(12)

建立基于月货运量数据的BP神经网络模型，采用3层网络结构，输入层5个神经元，隐含层包含15个神经元。前8年数据作训练集，后1年数据作测试集。优化算法采用Adam、激活函数采用tanh和损失函数采用MSE。建立基于日货运量数据的BP神经网络模型，同样采用3层网络结构，输入层1个神经元，隐含层6个神经元。前70%作训练集，后30%作测试集，其余参数与基于月货运量数据的BP神经网络模型相同。

表3为对比模型在测试集上的表现。

表2 LSTM预测结果评价指标

通过比较LSTM模型与对比模型分别在训练集和测试集上的表现发现：LSTM模型总体上优于时间序列模型和BP神经网络模型。其中，对于月货运量预测，在训练集上，ARIMA(0,1,1)(0,1,2)[12]的各项误差指标均优于LSTM模型和BP神经网络模型；但在测试集上的表现却差于后两者。这可能是由于宏观环境变化，2017年铁路运量有较大幅度回暖，但时间序列模型仅仅依据历史的趋势并未考虑这些客观因素。对于日货运量预测，BP神经网络和LSTM模型的预测误差虽然比较接近，但LSTM模型在测试集上的预测精度更高，模型的泛化能力更优。ARIMA模型在训练集上的误差很小，但测试集上的误差较大，这可能是因为测试集覆盖的时间段较长，随着时间的推移时间序列模型预测的误差变大。但LSTM在相同情况下表现出更高的预测精度，进一步体现了LSTM模型良好的预测性能。

表3 对比模型预测结果评价指标

图6 预测货运量效果对比

图6为分别各个预测方法的月货运量预测值和日货运量预测值与实际值的比较。其中，图6(a)直观表现出LSTM预测与BP预测效果接近，在2017年后的预测结果均优于时间序列预测，与上文分析结果相一致。图6(b)～图6(d)以实际运量为横坐标，预测运量为纵坐标。可以观察斜线的斜率情况(斜率越接近1，预测效果越好)直观判断各模型的预测效果：LSTM预测明显优于BP和时间序列预测。

4 结论

结合实际情况，本文主要建立了基于月货运量数据的LSTM多变量预测模型和基于日货运量数据的LSTM时间序列预测模型。前者考虑了影响因素对货运量影响的滞后效应，拥有较长时间的记忆能力，并能够有效学习影响因素与货运量的关系；后者则集中考虑货运量时间序列的序列依赖性，构建长时间序列的LSTM网络。为体现LSTM网络性能，分别建立了基于月货运量和基于日货运量的ARIMA模型和BP神经网络模型，通过对比以上模型在训练集和测试集上的预测结果指标，发现构建的基于月货运量数据LSTM多变量预测模型和基于日货运量数据的LSTM时间序列预测模型均拥有优秀的预测精度，体现了LSTM网络对长时间序列上的学习能力及泛化能力。LSTM网络在预测中的良好表现，为铁路短期货运量的预测提供一种预测思路，对铁路日常运输组织具有十分重要的意义。在接下来的研究中，可以改进LSTM模型，以进一步提高模型的预测精度。