钢轨打磨过程中磨石参数对钢轨温度场影响研究

张子舆，郭 俊，刘启跃，王文健

(西南交通大学 摩擦学研究所，四川 成都 610031)

随着我国铁路运营密度的加大，钢轨疲劳伤损(钢轨剥离、波浪形磨损、斜裂纹、焊缝飞边等[1])成为钢轨的主要伤损形式。目前针对钢轨表面疲劳损伤最有效的修复方法就是进行钢轨打磨[2-4]。钢轨打磨属于复杂的表面材料的去除工艺，包括滑移、变形、剪切、材料去除、热量产生及传递等过程[5-7]。在钢轨打磨过程中，不合理的打磨参数设置将造成大量的磨削热堆积在钢轨轨头部位，这将会使钢轨表面的温度上升[8]。研究学者发现：打磨过程中轨头温度过高将会导致钢轨发蓝[9](图1)，甚至可能改变钢轨材料的微观组织[10-12]，形成打磨马氏体组织。国外学者开展了很多有关磨削温度场的研究:Jaeger[13]首次提出“移动热源法”用以计算剪切滑移区材料的温度场；Outwater等[14]将磨削区视为沿着工件表面移动的热源，使得温度场的计算更准确；Rowe等[15]建立了磨削传热模型并研究了不同磨削参数对温度的影响。国内学者通过仿真和计算研究了不同工艺参数对钢轨打磨温度变化的影响：聂蒙等[16]提出增加砂轮直径和提高作业速度均能降低打磨温度，且打磨头数量的增加有利于打磨温度的稳定；张青等[17]指出打磨车移速越快、磨石转速越低，相应打磨温度越低；Zhang等[18]认为打磨温度随打磨功率的增加而升高，可通过提高磨削区宽度和打磨车移动速度来限制打磨温度的升高。

虽然，国外学者对磨削过程的热影响做了大量研究，国内学者也对钢轨打磨过程的温度场做了探讨。然而，磨石作为打磨机构的重要组成部分，其参数对打磨温度场的影响规律尚不清楚。因此，本文在数值计算基础上，利用Abaqus有限元仿真方法对打磨过程中不同磨石粒度、不同进给深度以及不同磨石转速对打磨温度场的影响进行了分析。仿真过程中参考文献[18]中的移动热源法，将打磨磨石视为移动热源，以此来求解打磨过程中钢轨的温度场。研究结果有助于为现场钢轨打磨选取合适的磨石参数提供理论指导。

图1 钢轨发蓝[9]

1 钢轨打磨过程传热原理

与传统的外圆磨削温度模型不同，钢轨打磨温度模型属于端面磨削[17]。打磨过程中，钢轨瞬态温度场的微分形式为

(1)

T(x,y,z,τ)=T0τ=0

(2)

式(1)右边是与温度相关的二阶导数，需设置两个边界条件。在磨石与钢轨作用边界上，有热流的流入，其边界条件为

(3)

在其他边界上为

(4)

式中：TE为环境温度；T为钢轨实时温度；n为钢轨界面向外的单位法向；h为对流系数，因对流方式不同，这个系数的取值也有很大的变化；ε为发射率，是表征辐射强度的物理量；σ为斯忒藩-玻尔兹曼常数；q为表面热通量，是打磨过程中磨石产生的打磨功率转化为的热量值。由式(3)和式(4)可以看出：接触区域有热流量的产生，而非接触区域钢轨仅通过辐射与对流与外界进行热量交换。

2 钢轨打磨有限元模型

2.1 打磨过程数值仿真模型

打磨磨石被视为持续发热的移动面热源，移动速度v与打磨车的行驶速度相同，典型的热源分布示意图见图2。由图2可知：热源模型主要有三种，分别是矩形分布、三角形分布和直角三角形分布。参照磨石与钢轨的接触过程，热源被假设成呈矩形分布。

图2 钢轨打磨热源分布模型[18]

钢轨打磨过程中打磨磨石由打磨电机驱动，根据能量守恒定律可知：磨石与钢轨接触区域由摩擦产生的热量是由打磨电机的功率转化而来。因此，磨石所产生的热流密度为

(5)

Q=Pm×τ×η

(6)

s=w×l

(7)

式中：Q为打磨过程总发热量；Pm为钢轨打磨电机功率；s为接触区域面积，即打磨磨石与钢轨接触的长方形区域；w为接触区域宽度，取10 mm[17]；l为接触区域的长度，取100 mm[18](各参数参照图2)；η为总发热量进入钢轨的比例，这个值一般无法定量测量，根据文献[19]η值假设为75%。

2.2 磨石参数与打磨功率关系

钢轨打磨磨石由许多颗磨粒组成。磨粒的粒度由磨粒刚好可通过的筛网尺寸决定。随磨石粒度的增加，磨粒尺寸减小，磨石越细；相反，磨石粒度小，磨粒尺寸增加，对应磨石较粗。可假设磨粒为圆锥形进行磨削力的计算[20]，则单颗磨粒磨削时的磨削力可表示为

Fet=kθ10.84h2.46v-0.299

(8)

式中：k为常数，取值5.4×10-4；θ为磨粒半锥角；h为磨粒切削深度，即每旋转一周，磨石沿垂直打磨面方向上的进给深度；v为磨粒切削速度。

打磨过程中，整块磨石与钢轨的接触形式见图3，其中磨石外径R和内径r间的圆环面为磨石有效打磨区域。

图3 磨石钢轨接触示意[21]

在实际的钢轨打磨作业中，打磨车移动速度远小于磨石的旋转速度[21]，故以磨石的线速度(ωr)取代式(8)中的磨粒切削速度(v)。因此，沿半径方向在磨石的有效打磨区域取微元，微元的磨削力[22]为

dFt=FetCslF(h)dr

(9)

(10)

(11)

式中：Cs为单位面积的磨粒个数；l为接触宽度为b时的接触弧长；F(h)为与进给深度相关的概率函数，当进给深度越深时，参与磨削的磨粒数就越多；μ为磨粒突出高度均值；σ为方差。

利用磨削力式(9)，通过积分法可以得出打磨过程中的磨削力矩为

(12)

不同力矩下的打磨功率为

(13)

得到打磨功率后，将功率值带入式(5)～式(7)，便可得到相应的热流密度值。

2.3 有限元模型

利用Abaqus建立钢轨打磨有限元模型，选取材料为U71Mn的75 kg/m钢轨作为仿真钢轨模型，钢轨长度3 m，模型见图4。为了在减少计算量和提高求解精度之间找到平衡，通过多次仿真发现：仅建立轨头部分的有限元模型就能计算得到准确的温度场数值，且计算时间更少。使用热传导分析步，通过DFLUX子程序加载移动的表面热流密度，加载平面见图4，模拟打磨过程中磨石在钢轨表面的移动。设定模型的散热边界条件为对流及辐射，设定网格单元类型为计算热传导的DC3D20(20节点二次热传导单元)，并在热流加载区域使用更加精细化的网格。钢轨材料参数及热仿真参数见表1。

图4 钢轨打磨温度场计算有限云模型

表1 钢轨材料及仿真参数

3 磨石参数对打磨钢轨温度场影响

3.1 进给深度

钢轨打磨过程中进给深度一般为8～14 μm。选择12#磨石,磨石转速为3 000 r/min，打磨平面宽度为10 mm，打磨列车速度为2.5 m/s，计算钢轨打磨中的温度变化，并绘制最高温度与进给深度的关系曲线，见图5。由图5可知，打磨钢轨的温度随磨石进给深度的增加快速升高。这是由于较高的打磨进给深度一方面导致单颗磨粒的磨削力增加，另一方面提高了参与磨削的磨粒个数。因此，随进给深度的增加，磨削力矩增加，打磨功率增加，引起更高的钢轨温升。

图5 进给深度对打磨温度影响

当进给深度为14 μm，磨石粒度为12#，磨石转速3 000 r/min，打磨平面宽度10 mm，列车速度5 m/s时选取钢轨打磨区域某一节点为温度监测点，考察该节点在打磨过程中的温度变化见图6。由图6可知，打磨开始后，节点温度先迅速升高到最高温度，然后慢慢下降，整个过程与打磨磨石相对该节点的位置变化相对应：当磨石靠近该节点时，打磨过程中的热效应导致该节点温度迅速上升；当磨石全部通过该节点时，打磨温度上升至535.7 ℃的最高值；当磨石远离该节点时，打磨温度逐渐下降。

图6 打磨过程中某节点的温度变化

打磨过程中整个钢轨的最高温度变化见图7。由于磨石转速较高，因此在打磨开始后，钢轨整体最大温度在0.04 s内迅速上升至535.7 ℃，并持续保持在稳定状态。由图7可知，钢轨温度迅速上升是磨石对钢轨持续的热流加载造成的，而当热流流入和热量损失达到平衡时，打磨热进入平稳状态，钢轨的最大温度保持稳定。

图7 钢轨整体温度随打磨时间变化

打磨过程中，钢轨整体温度仿真云图见图8。由图8(a)可知，钢轨温度呈椭圆形分布，在椭圆的中心部位最高，并向四周逐渐降低。这是由于打磨热产生于磨石与钢轨的接触区域，钢轨在越靠近接触区域的位置，其热传递效率越高，相应的温升越高、温度越大；而钢轨在远离接触区域的位置，温升主要来自于钢轨内部的热传导，由于传导过程中的热量损失，越远离接触区域的位置，对应温度越低。由图8(b)可知，温度云图呈碗状，温度在中心位置最高，并在远离中心位置的区域逐渐降低。

图8 打磨过程瞬时温度云图(单位：℃)

3.2 磨石转速

转速参数1 500～3 000 r/min、12#磨石,进给深度12 μm,打磨平面宽度10 mm,列车前进速度2.5 m/s下仿真得到打磨温度与磨削力矩随磨石转速变化的曲线，见图9。由图9可知，磨削力矩随磨石转速增加而降低，这是由于单颗磨粒的磨削力随磨石转速的升高而降低，导致磨石整体的磨削力矩下降。由图9可知，随打磨转速增加，打磨温度反而升高。由式(8)及式(13)中看出，这是由于转速升高对功率增加较大，而对磨削力下降的影响较小。

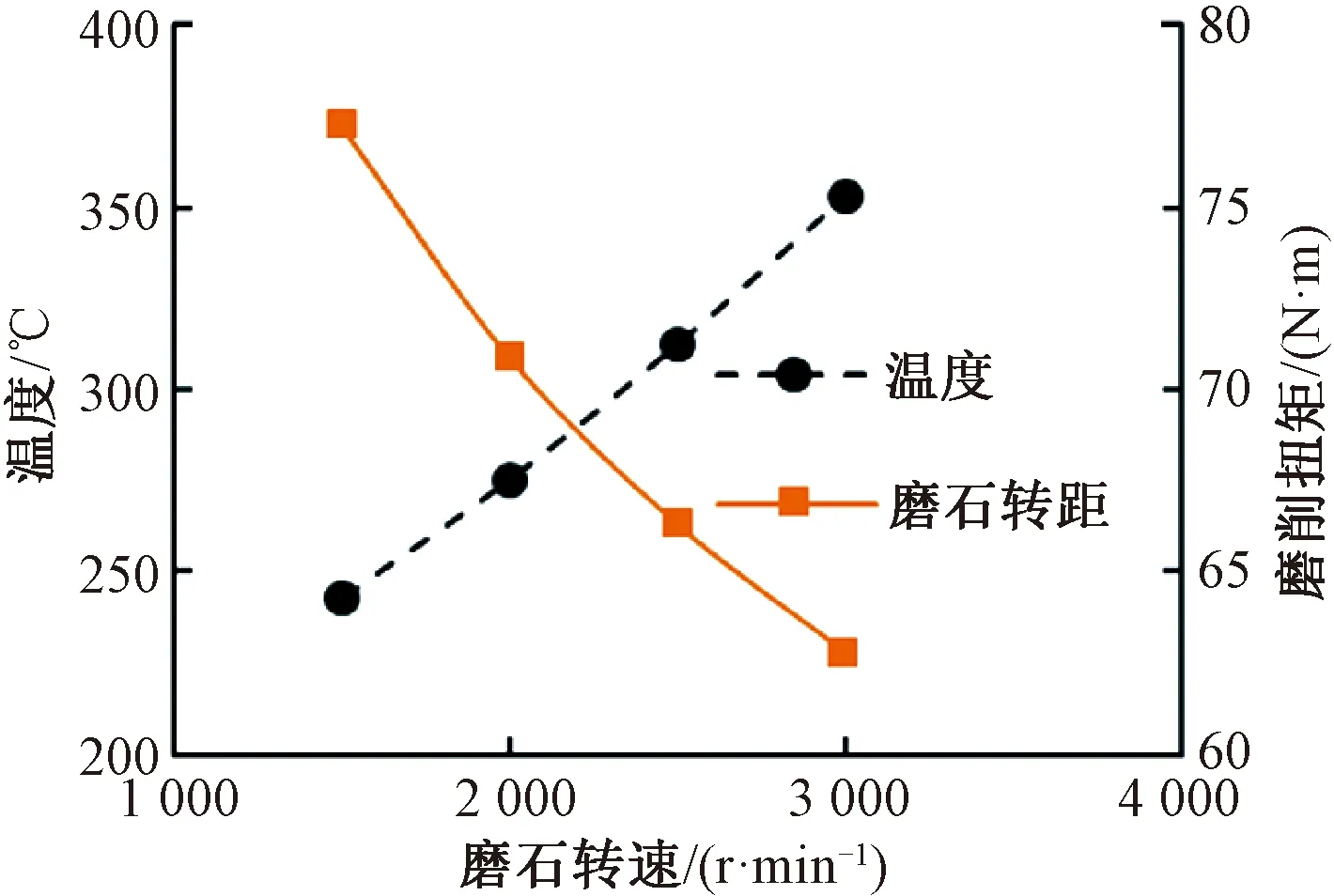
图9 磨石转速对打磨温度与磨削力矩影响

3.3 磨石粒度

明确磨石粒度与打磨温度之间的关系可以指导在现场打磨作业中选取合适粒度的打磨磨石。根据打磨磨石常用的粒度，选取12#、16#、24#、30#四种粒度参数进行仿真。其他仿真参数设置包括：进给深度为14 μm、磨石转速为3 000 r/min、打磨平面宽度为10 mm，列车前进速度为2.5 m/s。根据式(8)～式(13)和各粒度的特征参数[17]计算得不同磨石粒度对应的最大打磨温度，见图10。结果表明：随磨石粒度增加，钢轨温度呈现先上升后下降的变化趋势，四种磨石粒度中，16#粒度对应的最大温度最高。这一结果与文献[22]中“砂轮磨粒对磨削温度的影响”的有关描述相同，体现了仿真分析的正确性。这一规律与磨石粒度特征值的差异性有关：随着磨石粒度的增加，磨粒尺寸和半锥角减小，根据式(8)计算得对应的单颗磨粒磨削力减小；但随着磨石粒度的增加，磨粒数量也会增加，导致磨石整体的磨削力增加。因此，在12#～16#的粒度范围内，磨粒数量的增加相较单颗磨粒磨削力的减少对磨石整体磨削力的影响更大，而在16#～30#的粒度范围内则相反。

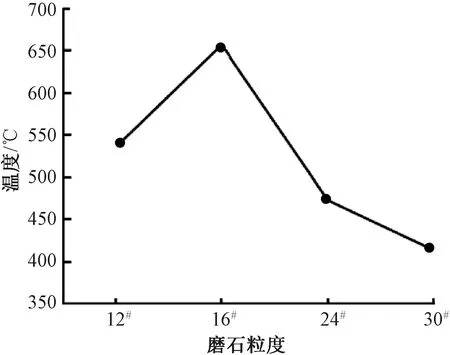
图10 磨石粒度与打磨温度关系曲线

4 结论

(1)基于单颗磨粒磨削力公式，利用数值积分方法，对打磨过程中不同粒度磨石所产生的打磨功率进行了计算。利用移动热源法将磨石视为在钢轨表面移动的热源，将功率等效为磨石打磨产生的热量加载在钢轨有限元模型上，对打磨过程中钢轨温度场进行了有限元仿真。

(2)当磨石进给深度从8 μm增加至14 μm，单颗磨粒的磨削力和参与磨削的磨粒个数均增加。导致打磨温度从164.5 ℃升高至535.7 ℃；由于转速对磨削力下降的贡献远小于直接对功率增加的贡献，因此，虽然在转速从1 500 r/min升高至3 000 r/min过程中磨削力矩从77.2 N·m下降至62.7 N·m，但温度却从242.5 ℃升高至352.9 ℃。

(3)随磨石粒度的增加，磨粒的半锥角减小，单颗磨粒的磨削减小，但磨石数量也会增加，导致磨石整体的磨削力矩增大，这种“竞争”的关系使得在磨石粒度从12#增加到16#过程中，打磨温度从535.7 ℃升高至656.7 ℃，当粒度从16#增加到30#过程，温度却逐渐下降到413.7 ℃。