基于AHP分析法的磁浮系统车轨耦合振动抑制方法

汪科任，罗世辉，陈晓昊，马卫华，邹瑞明

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

磁浮列车不同于有轨列车，是一种新型的轨道交通运行方式，具有运行平稳、乘坐舒适和无轨道接触等优点，具有较好的市场运用前景[1]。EMS型磁浮列车依靠电磁悬浮力实现稳定悬浮，悬浮力将悬浮间隙与悬浮电流耦合在一起[2]。由于悬浮电磁力同时作用在磁浮列车与轨道梁上，若悬浮控制器性能稍差，极易出现车轨耦合振动。美国AMT磁浮列车就曾出现过在刚度较强的水泥梁上能够实现稳定悬浮，而在刚度较低的桥梁上却失稳的现象[3]。针对该问题大量学者进行了相关研究，结果表明：刚度较低的弹性轨道梁是导致系统悬浮失稳的主要原因。为了防止悬浮系统在弹性轨道梁上悬浮失稳，工程应用中常常通过增加轨道梁刚度与质量来抑制车轨耦合振动，但从经济性的角度来考虑，增加轨道梁刚度与质量将导致轨道梁建设成本的大幅增加。现阶段在磁浮列车的整个造价中，轨道梁的建设成本高达60%～80%[4]。所以设计出性能更好的悬浮控制器来抑制悬浮系统在柔性轨道梁上的耦合振动，促进磁浮列车更好的商业化发展是非常必要的[5]。

车轨耦合振动常常发生在磁浮列车静悬浮或以较低速度通过弹性桥梁时，为抑制这种车轨耦合振动，国内外学者进行了大量的相关研究[6-16]。其大致可以分为以下2种：一种是从控制算法的角度对悬浮控制器进行优化设计，研究者认为悬浮控制器本身的特性是导致磁浮系统在弹性桥梁上失稳的主要原因；另一种是采用某种特定的算法对磁浮列车本身的系统结构进行优化设计，从而提高磁浮系统的动力学特性。文献[6]利用Simulink软件建立了HSST型五悬浮架磁浮列车垂向动力学模型，对比分析了不同悬浮控制算法对磁浮系统悬浮稳定性的影响，并指出不同的悬浮控制算法将对悬浮系统的稳定性产生不同的影响。文献[7-8]以单铁悬浮系统为研究对象，采用双环PID控制算法，从能量转换的角度解释了系统发生车轨耦合的原因。文献[9]利用状态观测器对悬浮电磁铁的速度进行了准确估计，通过动力学仿真得出：当悬浮控制器频率与轨道梁主频率接近时，悬浮系统将发生车轨耦合振动现象。文献[10]以单铁悬浮系统为研究对象，指出在一定程度上提高悬浮控制器的电气悬浮刚度可在一定程度上抑制系统的车轨耦合振动。文献[11-13]各自采用不同的控制算法，分别研究了车辆运行速度、轨道梁长度和轨道梁抗弯刚度等对磁浮列车动态响应特性的影响，从而优化了磁浮系统的动力学特性。文献[14]指出：采用越多的状态反馈，系统具有更优的动力学特性。文献[15]以单铁悬浮系统为研究对象，将车体对悬浮电磁铁的作用力视为额定的外界扰动，采用卡尔曼滤波实现了系统在弹性轨道梁上的稳定悬浮。文献[16]在文献[15]的基础上考虑了车体的振动，采用鲁棒控制器实现了系统在柔性梁上的稳定悬浮。然而，通过以上文献分析可知，在悬浮控制器设计过程中，鲜有文献对二次型加权矩阵权重系数的选取以及不同控制算法对磁浮系统车轨耦合振动的影响进行很好的机理说明。文献[17]通过对单悬浮架模型与单铁模型的仿真对比得出，对磁浮系统车轨耦合振动机理的探究，单铁系统是适用的。因此本文以弹性轨道梁-悬浮电磁铁-车体垂向耦合振动模型为研究对象,采用AHP法(层次分析法)程序化的求取了控制器二次型性能指标中状态加权矩阵的权重系数，并以此为基础分析了控制器1与控制器2对磁浮系统悬浮稳定性的影响。将采用轨道梁、悬浮电磁铁以及车体的振动状态进行主动控制的反馈控制器定义为反馈控制器1，将仅对悬浮电磁铁振动状态进行主动控制的传统控制方式构成的反馈控制器定义为控制器2，如文献[10，18-20]等采用的控制器。

针对磁浮系统中二次型性能指标中状态加权矩阵选取困难的问题，采用AHP法来程序化的求取该值，在此基础上利用二次最优控制理论设计出2种不同的状态反馈控制器，在一定程度上从能量激振的角度分析了2种不同状态反馈方式对悬浮系统车轨耦合振动响应特性的影响。

1 车轨耦合等效模型

针对西南交通大学常州轨道交通研究院某等效单铁悬浮系统(见图1)，取向下为系统正方向，根据牛顿第二定律可得轨道梁、悬浮电磁铁和车体在额定悬浮位置处的动力学方程为

(1)

(2)

(3)

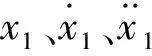
F=-Ps(x2-x1)+PiIM

(4)

根据Meisinger推导可得到系统电学方程为[2]

(5)

图1 简化的单铁-轨道梁-车体模型

悬浮电磁铁线圈两端电压与电流的数学表达式为

(6)

(7)

由式(6)、式(7)可得

(8)

将式(8)在额定位置处Taylor展开，得

(9)

式中：Um为实际加载在悬浮电磁铁线圈两端的电压；φ为流过悬浮电磁铁极面积的磁通量；Lm为电磁铁瞬时电感；cm为实际悬浮间隙；UN为平衡位置处电磁铁线圈两端的电压；c为相对额定悬浮位置气隙的变化量。

(10)

(11)

由于c=x2-x1，由式(10)、式(11)可得式(5)。

(12)

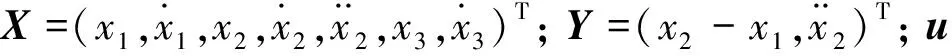
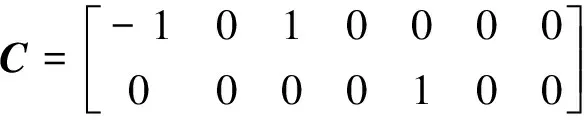
其中，

2 状态反馈控制器设计

2.1 状态反馈增益矩阵K的求取

磁浮列车在运行过程中常常出现悬浮控制器性能恶化现象，尤其在温度较高的夏季特别突出。根据相关分析，其主要是由悬浮控制器发热量较大引起的。所以在确保悬浮系统具有较好的动态响应特性的同时，如何限制悬浮控制器的发热量是非常必要的。幸运的是该问题可以通过线性二次最优控制理论来处理，通过该理论设计出的控制器能够实现系统控制能量与系统动态特性之间的平衡。定义被控系统(式12)二次型性能指标J为

(13)

PA+ATP-PBRu-1BTP+Q=0

(14)

式中：矩阵P为正定对称矩阵。状态反馈增益矩阵K为

K=Ru-1BTP

(15)

2.2 状态加权矩阵Q的求取

式(13)中，与控制输入矩阵Ru相比，状态加权矩阵Q的维数较高，导致其加权系数的选取通常比较困难，一般都是通过经验试凑，并没有统一的方法。本文采用AHP法来程序化的解决状态加权矩阵Q求取困难的问题。AHP法是一种科学计算各元素权重系数的方法，是在对复杂决策问题的本质、影响因素及其内在关系等进行深入分析的基础上将问题划分为目标层、准则层和方案层，同时对各层次的元素进行两两比较而最终确定各元素加权系数的一种数学分析方法，能有效地应用于难以用定量分析解决权重系数取值的研究课题[21]。其设计步骤为[22]

Step1建立控制指标的层次结构。选取系统二次型性能指标即式(13)作为目标层；反馈的状态变量作为准则层；以满足总体合理的一致性检验准则作为方案层。

Step2构造线性系统判断矩阵，用于确定两两元素的重要性比较。在判断矩阵的构造中主观加权比例系数的确定是关键，令Hij(无单位)为指标i与j重要性的比较值，其遵循以下准则：

(1)2个元素两两比较，若同等重要用标度1表示；稍重要用标度3表示；明显重要用标度5表示；强烈重要用标度7表示；极端重要用标度9表示。

(2)若2个指标的相对重要性位于2个比较值之间，则取值分别为2、4、6、8。

Step3计算每一层的权重并进行权重一致性的检验。若一致性比例系数ηR小于0.1，则认为系统通过一致性检验；否则需要重新规划各状态量之间的合理权重，直到其通过一致性检验为止。

令判断矩阵H(判断矩阵反映了设计者对各加权系数权重的分配)最大特征值相应的特征向量为WH，由于列车在实现稳定悬浮后，乘坐舒适性是列车运行品质中一个极其重要的指标，所以相对于其余状态变量的权重系数，与车体振动相关状态变量的权重系数应相对较大。由于反馈控制器1将系统的所有状态变量都进行了主动控制，其涉及的状态反馈量最多，设计也最为复杂，所以本文首先对反馈控制器1进行求解。

根据以上步骤可构造判断矩阵H为

对判断矩阵H每一列归一化后求行和再进行列归一化处理后可得判断矩阵H最大特征值对应的特征向量WH，为

WH=[0.124 00.140 80.155 30.043 90.136 2

0.199 9 0.199 9]T

(16)

根据式(17)可求取矩阵WH最大特征值λmax为7.488 1。根据式(18)求得一致性指标CI为0.081 35。其中n1为判断矩阵H的维数。由于判断矩阵H为7维矩阵，可知随机一致性指标RI为1.32[22]，带入式(19)可得一致性比率CR为0.062，其值小于0.1，可得判断矩阵的不一致性程度在允许的范围内，即通过一致性检验，则根据矩阵WH所确定的悬浮系统的二次型性能指标的权重系数是合理的，可用于式(13)中加权矩阵Q值得确定。

(17)

(18)

(19)

(20)

由式(20)可知，求取控制器2时，式(13)中状态加权矩阵的值有：Q2=diag(0.155 3,0.043 9,0.136 2)，最后结合式(14)和式(15)可求取控制器2为：u2=-K2X2。同理，由式(16)可知，求取控制器1时，式(13)中状态加权矩阵的值有：Q1=diag(0.124 0,0.140 8，0.155 3,0.043 9,0.136 2，0.199 9,0.199 9)，最后结合式(14)和式(15)可求取控制器1为：u1=-K1X1。系统结构间见图2。

图2 系统结构图

3 动力学仿真分析

3.1 系统闭环特征根分析

考查闭环系统稳定性有多种方法，如李亚普罗夫稳定性判据、劳斯判据等，而通过验证闭环系统矩阵特征根实部是否均为负数最直观，所以本文选取该方法来定性判断状态反馈控制器1、2对系统悬浮稳定性的影响。耦合系统相关参数见表1。若文中无特殊说明均选取轨道梁跨中位置，即x1=l/2作为静态悬浮位置。

基于AHP分析法，在反馈控制器1与反馈控制器2控制下闭环系统矩阵A特征根实部最大值变化规律，见图3。由图3可以看出，当轨道梁阻尼一定时，采用控制器1的反馈控制方式，当轨道梁刚度从500 ～1 500 kN/m递增的过程中，系统矩阵A特征根实部最大值均为负值，系统是稳定的。而采用控制器2的反馈控制方式系统矩阵A特征根实部最大值均为正值，系统是不稳定的。但进一步分析发现，采用反馈控制器2的控制方式，随着轨道梁刚度的增加，系统特征根实部的最大值是逐渐减小的，所以工程施工中通常采用大幅增加轨道梁刚度和阻尼的措施来抑制车轨耦合振动,但这将在一定程度上增加建设成本[15]。

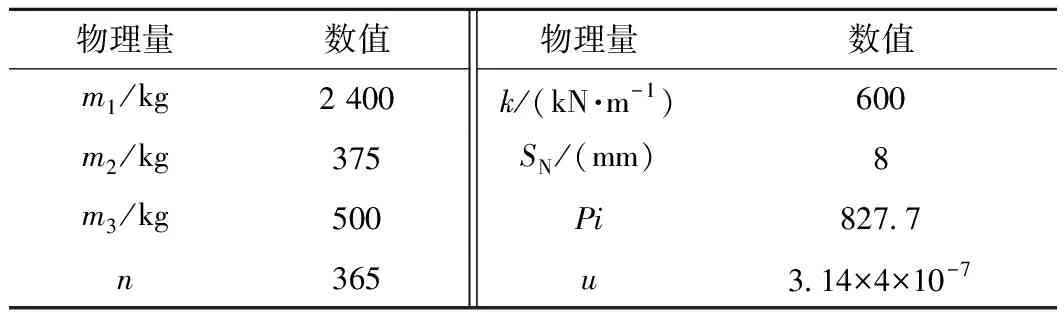
表1 系统参数

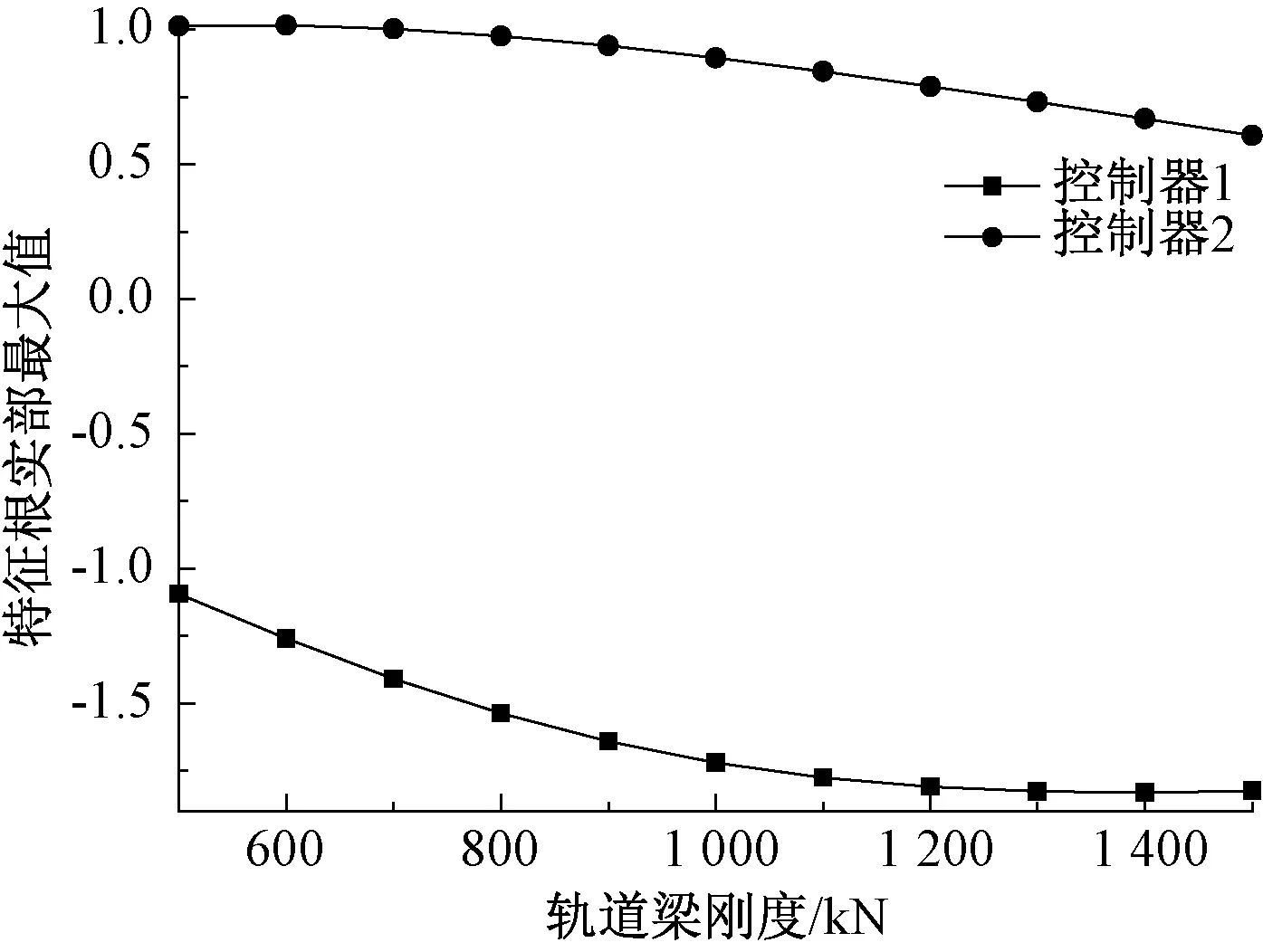
图3 特征根实部最大值

3.2 数值仿真分析

3.1节分析中对2种不同状态反馈方式进行了相应的定性分析，得出当轨道梁阻尼一定时，反馈控制器2不能使系统在较低轨道梁刚度下(如600 kN/m)实现稳定悬浮，而控制器1能够实现悬浮系统的稳定悬浮。所以这节将定量分析采用AHP法时控制器1在轨道梁刚度为600 kN/m时悬浮间隙、轨道梁位移，悬浮电磁铁位移与车体振动加速度的动态响应特性，分别见图4～图7。假设悬浮电磁铁初始位置距离轨道梁2 mm。根据式(14)～式(16)、式(20)可得控制器1与控制器2反馈增益矩阵K1、K2为

(21)

(22)

图4 悬浮间隙

图5 轨道梁位移

图6 电磁铁位移

图7 车体加速度

由图4～图7分析可知,对轨道梁、悬浮电磁铁以及车体的振动状态进行控制，将其振动状态引入状态反馈控制器的控制方式，基于AHP分析法能够实现悬浮系统在较低轨道梁刚度下的稳定悬浮，仅需约0.5 s便能实现系统的稳定悬浮，车体最大振动加速度仅0.18 m/s2。

3.3 能量激振分析

本节将利用文献[7]的方法，在一定程度上从悬浮系统对轨道梁能量输出的角度来分析采用反馈控制器1与反馈控制器2对系统悬浮稳定性的影响。由于磁浮列车-轨道梁耦合系统仅包括悬浮系统与轨道梁2个部分。根据对唐山磁浮线路的实际测量，轨道梁的振动特性可以用一定频率的正弦函数或余弦函数来表示[23]。由于能量的大小可以通过功率来反映，而功率的大小为作用力与被作用物体的速度大小的乘积来表示。为方便从能量的角度来探究不同轨道梁频率段车轨耦合振动的本质，这里不妨以轨道梁的速度作为输入，作用在轨道梁上的悬浮力作为输出。该传递函数可以表示为

HFV(s)=F(s)/V(s)

(23)

在某时刻，以振动频率为ω,振动幅值为0.2 m/s2,无相位差的正弦函数来模拟轨道梁的振动特性，即v(t)=0.2sin(ωt)。可知作用在轨道梁与悬浮系统之间的电磁力为

F(t)=0.2HFV(jω)|sin[ωt+∠HFV(jω)]

(24)

进一步分析可知，在一个时间周期内电磁悬浮力作用在弹性轨道梁上功率大小为

(25)

式中：T为积分时间。采用表1中的相关参数，式(21)、式(22)对应的控制器1与控制器2时，悬浮系统作用在轨道梁上的平均功率见图8。

图8 无轨道阻尼时悬浮系统输出功率

由图8可以看出，采用传统的控制方式即仅将悬浮电磁铁的振动状态进行主动控制，当轨道梁振动频率约低于50 rad/s时，悬浮系统向轨道梁输出能量，此时更容易激起车轨耦合振动。只有当轨道梁振动频率约高于50 rad/s时，悬浮系统才吸收轨道梁振动的能量，但对能量的吸收也相当少，最大仅有10 W左右。而采用将轨道梁、悬浮电磁铁以及车体的振动状态同时引入反馈控制系统进行主动控制的方式，在整个轨道梁振动频率范围内，悬浮系统始终不向轨道梁输出能量。同时在轨道梁振动频率为48 rad/s附近，悬浮系统对轨道梁的振动能量最大可吸收约为110 W。说明采用控制器1的反馈控制方式能够较好的抑制系统在低频段的车轨耦合振动。

由于实际的轨道梁还存在一定的阻尼，如果悬浮电磁铁向轨道梁输出的功率大于轨道梁阻尼消耗的功率，那么必然导致整个系统集聚的能量越来越大，从而导致整个系统悬浮失稳。忽略模态阻尼的非线性特性时，经计算轨道梁阻尼对桥梁的吸收功率为[23]

Pb=0.01ξωm1

(26)

式中：ξ为轨道梁阻尼比。当考虑轨道梁阻尼消耗的能量后，悬浮系统作用在轨道梁上的平均功率见图9。

图9 有轨道阻尼时悬浮系统输出功率

由图9分析可知，由于轨道梁阻尼消耗的功率十分有限，采用控制器2的反馈孔子方式，即使考虑轨道梁阻尼对轨道振动能量的消耗，当轨道梁振动频率低于50 rad/s左右时，悬浮系统仍然对轨道梁输出能量，最终必然导致悬浮系统失稳。而采用控制器1的反馈控制方式，悬浮系统在整个轨道梁振动频率段内都不向轨道梁输出能量，能保持系统较好的稳定悬浮。由表1可知，本文轨道梁振动圆频率约为16 rad/s，由图9可知在该频率段内，采用控制器2的反馈控制方式，悬浮控制器将向轨道梁输出能量从而导致悬浮失稳。

4 结论

针对弹性轨道梁-悬浮电磁铁-车体垂向耦合振动模型，通过本文的仿真分析可得出以下结论：

(1)基于AHP法，在一定程度上可程序化的求取系统二次型性能指标中状态加权矩阵权重系数求解困难的问题，且能实现系统的稳定悬浮。

(2)在轨道梁阻尼一定时，当轨道梁刚度较低时(圆频率较低时)，仅对悬浮电磁铁的振动状态进行主动控制，悬浮系统可能向轨道梁输出能量，从而引入系统出现车轨耦合振动。但随着轨道梁刚度的增加，悬浮系统将吸收轨道梁的振动能量，从而抑制系统的车轨耦合振动，可能这也是工程中常常采用增加轨道梁刚度来抑制车轨耦合振动的原因。

(3)在轨道梁阻尼一定时，采用将轨道梁、悬浮电磁铁以及车体的振动状态引入反馈控制器进行主动控制的方式，悬浮系统能吸收轨道梁输出的能量，从而抑制车轨耦合振动。同时能够实现系统在低轨道梁刚度上的稳定悬浮。