基于离散单元法的碎石集料动力变形特性研究

2020-12-07王鹏程刘建坤叶阳升张千里

铁道学报 2020年11期

王鹏程，刘建坤，叶阳升，张千里

(1.中国铁道科学研究院集团有限公司铁道建筑研究所，北京 100081；2.中山大学土木工程学院，广东广州 510275)

碎石集料作为铁路道砟以及路基填料等在铁路工程中获得了大量的应用，承受着列车荷载的往复作用，所引起的沉降变形严重影响着行车舒适性、安全性与长期服役性[1]。碎石集料的动变形特性可以通过永久变形和回弹变形两个方面进行描述。其中，回弹变形特性可以采用回弹模量MR评价，其定义为循环荷载作用下，偏应力与可恢复的弹性应变的比值[2]为

(1)

Selig等[3]进行了大型动三轴试验，研究了循环荷载作用下的道砟集料的变形特性，结果表明，轴向应变及回弹模量随着荷载作用次数的增加而增加，并最终趋于稳定，集料在密实的同时持续硬化。Stewart等[4]基于大型动三轴试验，研究了荷载形式对集料永久变形的影响，结果表明：永久变形随幅值的增加明显增加，第一次加载所引起的永久变形最大。Akke等[5]基于室内试验分析了荷载幅值对动变形的影响，认为在动荷载幅值较低时，集料几乎不发生塑性变形。Shenton[6]研究了加载频率对于塑性变形的影响，认为频率对于塑性应变几乎没有影响。Indraratna等[7]基于大型三轴试验的结果认为道砟的累积塑性应变随频率的增加而增加。

除外部荷载外，集料的密实程度和孔隙状态也对动变形影响显著。Lekarp等[8]研究认为密实状态的微小降低都会引起集料塑性应变的明显增加。

在针对碎石集料的研究方法方面，除了大型室内试验以外，基于离散单元法、非连续变形分析法等数值分析手段也获得了广泛的应用，特别是以颗粒流软件PFC3D(Particle Flow Code)为代表的数值分析软件，在碎石集料力学性质的分析中体现出了较高的效率与精度[9-10]。

本文基于颗粒流计算方法建立了碎石集料的动三轴剪切试验模型，通过对比室内试验结果对模型进行了标定与验证，进一步地分析了动荷载形式、集料密实状态对于整体动变形特性的影响。

1 颗粒流模型的建立与验证

1.1 颗粒流试样生成

颗粒流模型中，可用无摩擦的刚性圆柱墙体单元模拟三轴侧边界，用颗粒单元模拟碎石块体。上下界面同样采用刚性墙体模拟加载板。计算时上下界面同时加载，通过伺服程序监测颗粒与侧边界的接触力并缩放侧边界墙体的半径保证恒定围压。

颗粒流模型中的基本单元为球体单元，采用clump命令生成不规则块体模拟碎石颗粒[11]。本文分别针对三种粒径级配的碎石集料进行了分析，级配A、B、C分别为1.27～2.54、2.54～3.81、3.81～5.08 cm。直接按照粒径大小生成颗粒后再替代为clump块体，完成试样制备。

生成的三轴试验的颗粒流模型见图1(a)，试样高0.6 m，底面直径0.3 m，不同颜色单元代表不同形状的块体单元。三轴剪切前试样内部的接触力分布见图1(b)，力链分布较均匀，试样内部块体颗粒接触良好。

通过对比试验结果并进行调整，选择线刚性接触模型描述颗粒间的接触，最终确定的模型参数见表1。

表1 三轴试验细观参数

1.2 室内动三轴试验

为了验证颗粒流模型，进行了大型室内动三轴剪切试验。室内试验所采用的三轴试验系统见图2，试样高度0.6 m，试样底面直径0.3 m。试验过程中所用的集料及筛分设备见图3，铁路道砟经筛分后形成相应粒径级配的集料。

图2 室内试验装备

图3 试样材料与筛分设备

数值计算及室内试验均施加10 000次的循环荷载。在颗粒流计算过程中，不能直接对墙体施加荷载，本研究编制了伺服程序对上下墙体单元的目标应力进行控制，通过调整上下墙体的位置实现动力加载。根据相关研究，将列车荷载简化为半正弦荷载[12-13]，见图4。

图4 动荷载形式

进一步地，可以将图4所示的动荷载写为

(2)

式中：σreq为墙体的目标控制应力;T为动荷载的周期。

1.3 模型验证分析

室内试验与颗粒流模型计算得到的，循环荷载条件下，碎石集料的轴向累积塑性应变εap及回弹模量MR的变化情况，如图5、图6所示。

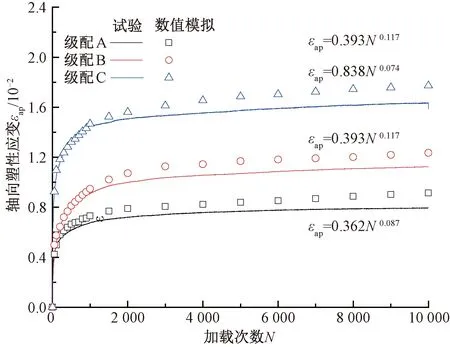
图5 轴向累计应变与加载次数的关系

图6 回弹模量随加载次数的变化

动荷载作用下，εap和MR的变化规律基本一致，在动荷载作用初期，增加速率较快，并随着加载次数的增加而持续增加，但速率不断减小，并最终趋于平稳。

与室内试验结果相比，数值计算得到的永久变形偏大，主要是受颗粒棱角度和模型侧边界的影响，数值模型的颗粒间缺乏足够的嵌挤与摩擦，因此产生了较大的塑性变形[14]。数值计算结果可以较好地反应不同粒径集料的永久变形情况，并展开进一步计算分析。

2 动荷载形式的影响

本部分研究了荷载条件对集料动变形特性的影响，颗粒级配为3.81～5.08 cm。计算方案见表2，分别选择四种围压水平、幅值和频率值，利用围压、幅值与加载频率的数值组合来描述某一计算工况。相应的动荷载形式见图7。

表2 动荷载影响计算方案

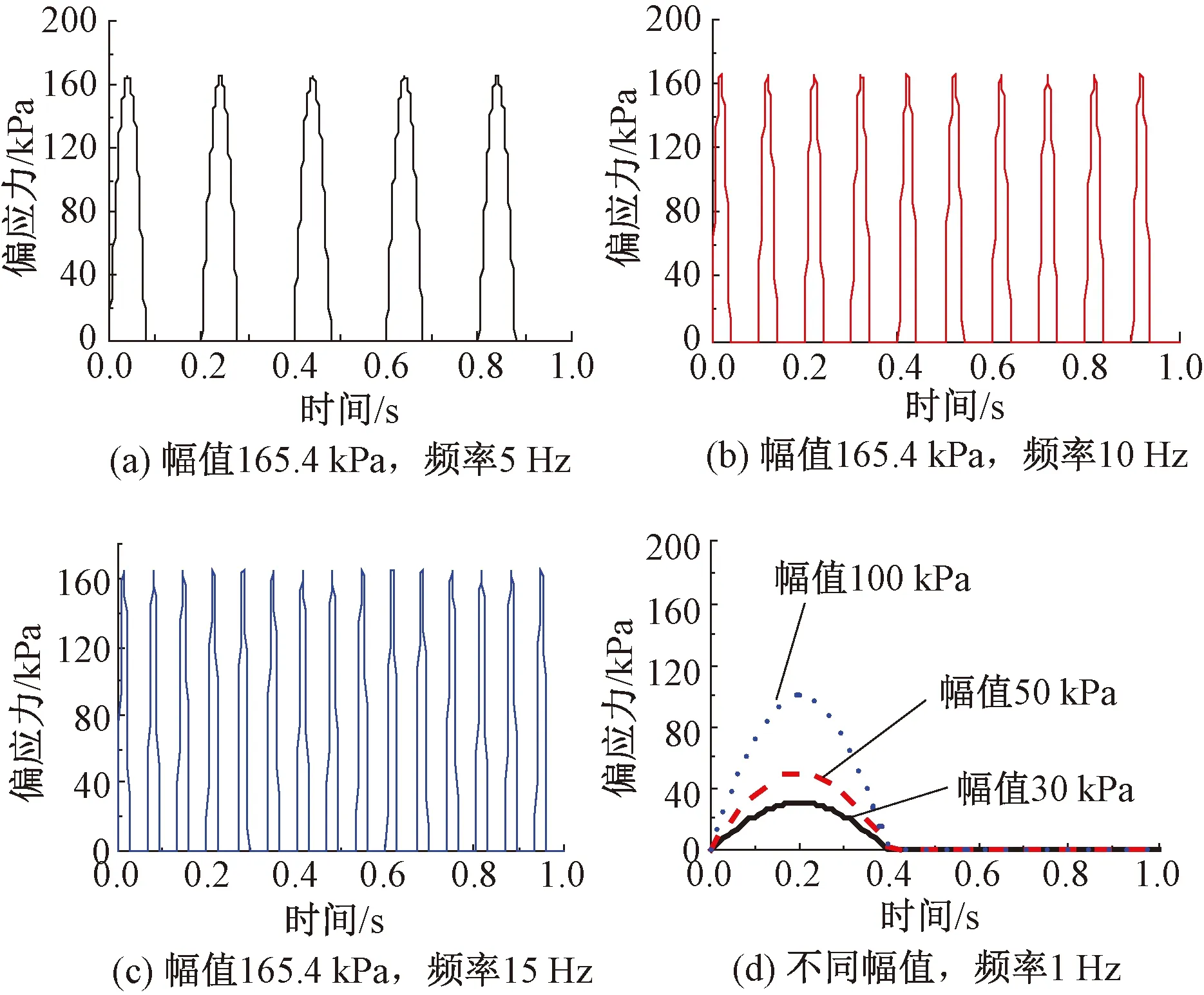
图7 不同动荷载形式

数值计算得到的荷载频率为1 Hz时，不同围压以及荷载幅值条件下，集料的累积轴向应变情况，见图8。集料的累积轴向变形随幅值的增加而持续增加，动荷载作用初期最为明显，随着荷载次数的增加，趋于稳定。

图8 荷载幅值对轴向变形的影响

数值计算得到的荷载幅值为165.4 kPa时，加载频率对于永久变形的影响，见图9。随着加载频率的增加，集料的永久变形也明显增加，其增加的幅度也在增加。

图9 加载频率对轴向变形的影响

碎石集料的回弹模量MR随荷载作用次数变化较大，随着集料持续密实，最终趋于稳定，此时，回弹模量只与集料所受到的应力水平有关。因此可针对加载次数为N=10 000次时的MR展开分析，多种动荷载形式下的级配C集料的MR与应力不变量θ的关系见图10，采用k-θ模型进行描述，模型拟合结果列于图中，随着应力不变量θ的增加，回弹模量持续非线性增加。

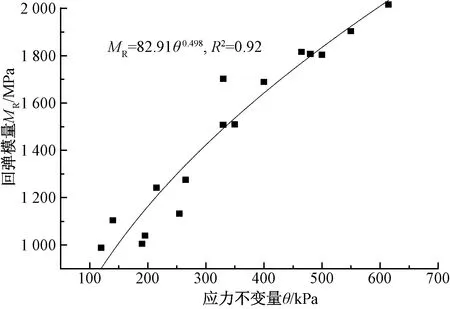
图10 回弹模量与应力不变量的关系

3 孔隙状态的影响

针对细粒含量对砂土力学性质的影响研究表明，相比于整体密实状态，大粒径骨架颗粒之间的相互咬合、嵌挤与摩擦的影响更加显著[15-16]。为了评价孔隙状态对含细颗粒的间断级配碎石集料整体力学性质的影响，提出了骨架孔隙比es的概念，其定义为碎石-细砂石间断级配混合料中孔隙体积与大粒径骨架碎石颗粒的体积比。

集料的整体孔隙比e为孔隙的体积与固体颗粒体积之比为

(3)

式中：Vgs和Vrs分别为小粒径的砂石颗粒以及大粒径的碎石颗粒的体积；Vv为孔隙的体积。

小粒径砂石含量m为砂石的质量与混合料总质量的百分比为

(4)

式中：ρgs和ρgs分别为砂石颗粒和碎石颗粒的密度，本研究中分别取为1 950 kg/m3和2 650 kg/m3。

进一步推导出式(5)所示的关系，其中w表示砂石与碎石颗粒的体积比为

(5)

则可以推导出式(6)和式(7)所示的结果为

(6)

(7)

则根据骨架孔隙比的定义可以推到出其计算公式为

(8)

为分析孔隙状态对动变形的影响，进行了颗粒流三轴剪切计算分析，动荷载见图4，试验围压55.1 kPa。

混合料中大颗粒粒径为3.81～5.08 cm，细颗粒粒径为1～10 mm，计算方案如表3所示。在相同的整体孔隙比条件下，加入5种含量的细颗粒配置混合料进行研究，并计算出相应的骨架孔隙比。

表3 孔隙状态影响计算方案

计算得到的不同整体孔隙比级配C集料的动应力-应变曲线见图11，荷载作用次数为100。整体而言，随着孔隙比的增加，集料在第一次动荷载作用下的轴向塑性应变在不断增加，在100次动荷载作用后，塑性应变随孔隙比的增加趋势更加明显，对应于孔隙比为0.46、0.54、0.68、0.74时的塑性应变分别为0.47、068、1.09、1.71。随着轴向应变的增加，动应力应变的斜率在不断增加，反应的是回弹模量的不断增加，而随着孔隙比的增加，曲线的斜率也在增加，说明孔隙较大时，在荷载作用下孔隙被不断压缩的同时以塑性变形为主，回弹变形则相对较小。