无车承运人参与下的公铁联运主体利益博弈研究

康凤伟，李雪梅，李金宇，周逸薇

(1. 北京交通大学 经济管理学院， 北京 100044； 2. 神华铁路装备有限责任公司， 北京 100011)

随着现代社会中客户对运输要求的提高和我国交通运输网络的不断完善，多式联运已经成为我国交通运输体系中的重要组成部分。与单一的公、铁运输方式都存在着明显的局限性相比，公铁联运不仅能够实现公路与铁路运输的优势互补、降低物流成本，而且可以提高交通基础设施资源的利用率、优化我国交通运输体系。在现有公铁联运的发展阶段下，更需要不断提高公、铁二者运输方式的一体化程度和主体间协作水平，从而实现系统效益的最大化，充分发挥公铁联运运输优势。公铁联运是指采用公路及铁路两种运输方式，在多方运输主体参与下，由全程运输承运人把货物从接管货物的地点运至指定地点交付的运输方式[1]。公铁联运可分为多种模式，从决策方式上看，可以分为集中决策和分散决策；从经营方式上看，可以分为公路企业、铁路企业和无车承运人分别作为经营方的主导模式。以经济学的视角分析，公铁联运内部业务交互是上述主体间的持续博弈、相互选择的过程，在这一过程中不同参与主体会根据自身经营条件与市场实时变化采取相应的措施，以确保自身利益最大化。

当前，关于公铁联运问题研究涉及多个方面。相比于传统运输模式，公铁联运由干线与支线运输共同组成，因此需要对公铁联运中的干线运输服务计划、货运量的设计以及定价方案等决策进行综合优化[2]。补贴政策作为一种有效的扶持新兴行业的政策，被广泛地应用，是公铁联运初期有效运行的有力保障，然而不同补贴额度对于提升公铁联运运输竞争力的影响是有限的[3]。公铁联运过程中涉及多个运输主体，为解决铁路物流中心和各配送点以及客户之间复杂的供给与需求关系，也需要关注配送方案的优化问题[4]。同时保证在有限的交通基础设施基础上对公铁联运设计优化，确保在有容量限制下最大可能的提升网络的运输[5]。公铁联运运输任务分配及运输网络优化研究是近年来关注的热点，学者们也采用包括目标优化算法、启发式算法、模糊方法和混合方法来解决这一问题。Uddin等[6]对大型公铁联运网络的货运运输分配进行了研究，针对运输网络扩展计划设计出基于路径的分配算法。Verga等[7]基于图论网络的数学表达方式，求解出考虑多种影响因素的多式联运任务分配问题。城市规划和铁路货运之间一直有着紧密的联系，考虑城市地方政府对可持续模式转变战略的重视程度。扶持公铁联运的市场是改善环境、提升城市潜力的一种有效手段，同时地方城市交通规划对促进公铁联运货运具有重要的促进作用[8]。Carboni等[9]以实际运输网络数据为依据，将公铁联运覆盖的服务距离设为主要指标，对联合运输的技术经济竞争力进行评价。Stackelberg定价博弈模型是解决多主体间利益协同问题的最广泛的方法之一，该模型考虑了不同主体间博弈次序与主导地位的情形，在运输主体博弈、供应链系统协调方面有着广泛应用。段华薇等建立特点不同两种市场结构下的高铁快递和传统快递的博弈模型，通过对比二者最优协议运量和市场运价策略，算例结果验证了模型的有效性[10]。在此研究基础上，杨雯等[11]将期权理论引入高铁快递和传统快递公司的定价模型中，分析传统快递公司的期权最优订购量以及高铁快递公司最优定价策略。在公铁联运效益分析方面，段华薇等[12]将随机市场需求函数考虑进模型，探讨了公路企业和铁路物流中心作承运人的公铁联运定价策略。本文基于既有研究，对模型作适当简化，立足完整的“门到门”公铁联运运输流程，利用数值模拟论述无车承运人参与公铁联运业务并协调公、铁运输企业的优越性。

本文以公路、铁路及无车承运人参与的货物运输服务链条作为研究对象，对分散决策下公铁联运不同参与主体作为承运人情形下运输链条的经营效益进行分析。在考虑市场需求不确定性的前提下，构建3种模式下的公铁联运物流服务链的主体间博弈模型，根据各方利润最大化目标和主导权的不同，测算最优协议运价、最优协议运量和最优利润，并对影响公铁联运参与主体决策因素进行分析。

1 传统公铁联运模式下的收益分析

1.1 问题描述

本文将重点对比讨论无车承运人参与与否的不同情形下的公铁联运组织结构。在传统公铁联运模式下即不存在无车承运人参与运营时，联运主体仅为公路和铁路运输企业，此时运输企业需要独立面向市场，完成揽货业务的同时还需要与另一方运输企业达成协作，按一定的协议运价购买对方的运输服务。博弈的具体顺序可描述为：在一个单位运价固定为p的运输市场中，市场随机需求为x服从分布函数为F(x) ，密度函数为f(x)，期望为μ的概率分布，公铁联运负责市场经营的一方(公路r或铁路t)负责承揽市场客户的门到门的运输业务，经营方根据历史数据所得的预测需求量提前与协作企业以运价w向协作企业购买协议运量q的与订承运协议来补足自己的运输短板，公路运输倒短的成本为c0，铁路运输成本为cr。在这一过程中运营方所面临的问题是，一旦实际揽货量小于从合作方购买的运输量则会造成空运浪费，反之，揽货量大于购买的协议运量，则不能按计划完成运输的货物，需要更大的成本来完成运输任务，若公路企业为承运人，则成超出协议部分的全程公路运输成本用ct表示，若承运人为铁路或者无车承运人，则这一部分成本在现实中体现为运输时效性惩罚或者额外单独购买运输服务的惩罚e，其中e>ct>cr+c0。例如在公路作为运营方的情形下，当协议运量大于市场需求时，由于公铁联运中铁路运输需按运行计划准时发车，公路企业仍需要付出运价成本给铁路企业；当协议运量小于市场需求时，公路需要更高的全程公路运输成本ct独自完成运输业务。同理，在铁路作为运营方情形下的相关运输业务流程相同。本文假设市场价格为常量，不随需求而变化，相应的价格成本单位为元/t。

1.2 基本假设及变量定义

假设1公铁联运运输链条中仅由一家铁路企业与一家公路企业组成。

假设2参与主体了解博弈过程中的所有信息。

假设3负责集货的运输企业先根据市场需求与市场价格对运量进行决策，另一方再对协议运价和协议运量进行决策。

2 集中决策博弈模型分析

集中决策是指决策者(承运人)以运输链条所有企业的整体利益最优为目的进行决策，各参与主体以运输系统总收益最大化为目标。公、铁运输企业之间的协议运价相当于系统内部的资金转移，对系统的收益增量不产生影响，公铁联运系统中只有对外运输的成本。当市场需求量小于协议运量时，运输供应链的总利润为承运人揽货的总收入减去铁路与公路运输的总成本；当市场需求量大于协议运量时，超出部分需要以更大的成本进行运输(由原来的成本更低的公铁联运转为全程成本更高的公路运输)。所以供应链的总利润为承运人揽货的总收入减去由铁路运输承担的协议运量部分的成本、短驳运输成本和超出协议部分的全程公路运输成本。依据以上分析，在仅有公路与铁路企业参与的供应链的利润函数为

( 1 )

为了便于分析，将式( 1 )分段函数改写为

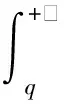
( 2 )

求解maxπC(q)所对应的q值，即为集中控制模式下的最优决策

此时供应链的最大利润为

( 3 )

可见，最优协议运量与公、铁路运输企业的单位成本和实际需求量的分布有关。最优协议运量与铁路运输成本成反比，与公路全程运输成本成正比。最优协议运量与公路短驳成本、铁路运输成本成反比，与惩罚成本成正比。惩罚成本越高(惩罚成本理论上大于公路短驳运输和铁路干线运输的总成本)。

3 分散决策下Stackleberg博弈

与集中模式不同，在实际市场中，公路与铁路运输企业在联运中各自独立经营，均以自身利益最大化为准则。系统实现利益协调的标准在于使得最终的结果趋近于集中决策的结果，分散决策分为公路与铁路运输企业分别作为承运人的情形进行讨论。

3.1 公路企业作为承运人

公路企业作为承运人时，公路运输企业是公铁联运系统中直接与市场客户接触的一方。公路企业首先向合作的铁路运输企业按照铁路运价wr购买数量q单位的站到站的运输服务，并按照市场价格p在市场中进行集货承运零散客户门到门的运输任务。铁路运输企业以较低的运输成本cr进行干线运输，公路运输企业负责短驳的支线运输，由于短驳运输成本相对较小，为便于分析，公路企业的支线运输成本忽略不计。当公路方向铁路企业预定的协议运量大于市场需求时，所有货物均可由铁路运输到达；反之，公路运输企业需以较高成本ct以全公路运输的方式自己完成超出协议运量的部分。其中，ct>wr>cr。

公路运输企业作为物流服务供应链的需求方，其分段利润函数为

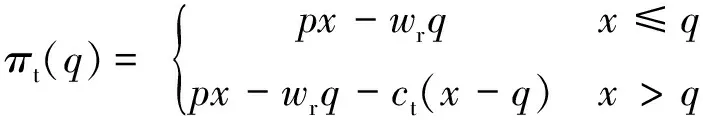
( 4 )

考虑利润函数的期望值，进一步对式( 4 )改写

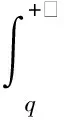
( 5 )

此时铁路运输企业的利润函数不受市场随机需求变化的影响，可表示为

πr(wr)=(wr-cr)q

( 6 )

公路企业依据市场价格和铁路方的协议运价来确定向铁路企业预定的协议运量。通过利润函数πt(q) 对协议运量wr求导并令其为0，可得铁路方的协议运价为

( 7 )

依据逆向归纳法，将式( 7 )带入铁路运输企业利润函数中可得

( 8 )

3.2 铁路企业作为承运人

与公路承运人类似，当铁路运输企业作为承运人时，铁路运输企业作为运输承运人，需要负责零散客户的揽货与运输任务安排。铁路企业为保证“门到门”的运输业务，需与公路企业预定短驳运输的协议运量并支付公路企业费用。当铁路企业与公路企业签订的协议运量大于市场需求时，所有货物均可由铁路和公路共同完成门到门运输；当协议运量小于市场需求时，公路企业不能完成所有货物的短驳，铁路企业需要另寻他法完成短驳，影响了门到门业务效率，这会降低铁路公司客户的满意度，给铁路运输企业的信誉带来损失，铁路企业需要承担相应的惩罚成本e元/t。

此时铁路运输企业直接面对市场客户，是公铁联运物流服务的供应商,其利润函数描述为

( 9 )

利润函数的期望值为

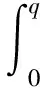
(10)

此时，公路运输企业的利润函数不受市场随机需求变化的影响，可表示为

πt(q)=(wt-c0)q

(11)

由于公路负责短驳，运行距离短，本文中按成本为元/t核算，所以这里的c0远小于铁路的单位成本cr。铁路运输企业主导下，公路运输企业确定协议运价，铁路运输企业根据给定的协议运价确定协议运量。

πr(q)对协议运量求导并令其为0，得到协议运价与运量的关系为

(12)

根据Stackelberg博弈的逆向归纳法，先对公路运输企业的最优协议运价策略进行分析。公路运输企业利润函数为

(13)

4 无车承运人参与下的公铁联运博弈模型

无车承运人是指无营运车辆却有承运能力的货运从业者，在无车承运人、公路运输企业和铁路运输企业组成的三方合作利益共同体可以实现多方主体在运输环节、运价调整、信息共享等环节的协调。在整个联运过程中，无车承运人负责揽货和对铁路与公路车源的组织调度，在承担货主货运交付任务的同时，需要对公、铁运输企业的换装环节与运输过程进行协调与监管，为客户提供一体化的公铁联运物流服务。在此阶段，由铁路物流中心对公铁联运业务进行协同管理，公路运输企业发挥其“门到门”的配送运输效用，而铁路运输企业也可以更专注于铁路干线运输，与仅有公、铁路企业参与的公铁联运相比，该阶段无车承运人、公、铁运输企业三者分工更为明确、各自优势发挥更为充分。

此博弈过程可描述为：无车承运人根据按市场价格p承运客户的运输需求，并根据需求预测以协议运价wr、wt分别与公、铁运输企业签订协议运量q。博弈的顺序为运输企业先确定协议运价；无车承运人根据运输企业的协议运价、市场价格和对揽货量的预期对协议运量进行决策。与之前的模型假设相同，当协议运量大于市场需求则可以保证所有货物运输，但剩余运量会增加无车承运人的成本；当协议运量小于市场需求时，则无法保证客户货物运输服务质量从而给无车承运人造成每单位e惩罚。

无车承运人、公、铁三方合作模式下，无车承运人面向客户揽货，然后与公、铁路运输企业分别签订运输协议，无车承运人的利润为

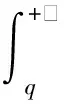
(14)

公、铁路运输企业利润函数分别为

πt=(wt-c0)q

(15)

πr=(wr-cr)q

(16)

式中：c0、cr分别为公、铁运输企业的单位运输成本。由于双方都是理性的，合作的基础为双方都有获利，所以wt≥c0，wr≥cr。

(17)

公路与铁路运输企业需要结合式(17)来确定自己的最优协议运价。因此，公、铁路运输企业在第一阶段的问题为分别求解maxπr(wr)、maxπt(wt)所对应的w值，得到最优协议运价为

(18)

(19)

将wr+wt=e-eF(q)代入πt、πr得

πt=(wt-c0)q=(e-eF(q)-wr-c0)q

(20)

πr=(wr-cr)q=(e-eF(q)-wt-cr)q

(21)

e[1-F(qT)]-(cr+c0)-2eqTf(qT)=0

(22)

综上，最优协议运价分别为

(23)

(24)

公铁联运无车承运人的利润可表示为

(25)

其中，最优协议运量qT满足式(22)。

通过上述模型分析，在无车承运人参与的分散决策下各主体以自身利润最大化为决策目标时，系统的最优协议运量和与集中决策下的最优协议运量相同。假设不存在延时运输与运输量整合的情况下，各决策变量与公、铁运输成本和惩罚成本的单调性分析与集中决策模型的结果分析一致。以公路作经营人为例，若公路企业掌握主导权，其会预定较多的公铁联运运输服务，铁路企业对其反映，会无约束的制定极高的协议运价，致使合作无法开展。根据主导权和决策顺序的不同，推导和分析了不同经营人下最优协议运量、最优协议运价与成本参数等的函数关系，当确定货品的市场需求函数时，可以确定对应的最优决策变量。

5 算例仿真

5.1 不同承运人收益算例分析

为验证模型的相关结论，本章内容结合实际运营中的神池南至李天木段朔黄铁路货运线路的调研数据，以算例分析的方式对模型的结果进行数值算例验证。对比分析不同模式下的最优协议运量、协议运价决策及利润情况。由于最优协议运量与成本和需求量分布函数有关，最优协议运价与成本和最优协议运量的分布函数值有关。所以，需求量的分布函数至关重要，为方便讨论本文假设需求量x服从a=100,b=1 000即U[100,1 000]的均匀分布，市场需求均值为550，则x的分布函数和概率密度分别为

根据分散决策不同承运人主导下最优决策变量公式，分散决策模式下最优决策变量汇总见表1。

表1 均匀分布下不同企业作为承运人下的分散决策结果

朔黄铁路神池南至李天木段运距516 km，主要服务于两地及周边城市的PVC、化肥、粮食等非煤品等商品的运输业务，两地上述货物的市场公路运输价格常年维持在100元/t左右。目前朔黄铁路运价依据《铁路货物运价规则》运价方案，整车货物每吨运价=基价1+基价2×运价公里。神池南至李天木段运价为66.8元/t，包括固定成本和单位变动成本在内的铁路运输总成本为29.9元/t。假设铁路起始点两地货站距用户需要短驳距离约为100 km，公路单价为0.16元/(t·km)，则朔黄线公路全程(干线加支线)经测算运价p为98.6元/t。这里我们将完成两地运输的市场价格统一采取100元/t。按照利润率50%计算，单独公路完成全程616 km运输成本为50元/t，公铁联运站到门的短驳运输成本为8元/t。

表2 神池南—李天木货运市场初值设定

首先将上述成本信息代入集中决策下的系统模型中，得到在公铁联运企业采取统一决策时的订货量为461.26 t，接近市场需求分布的均值，系统总利润为28 630.4元。

表3 神池南—李天木分散决策利润分析

5.2 结果分析

根据实证分析结果，同样都是在现实经营中的分散决策下，存在无车承运人供应链最优的，可以实现协议运量和总利润最大化，这是符合实际预期的。因为无车承运人作为第三方，负责揽货和协调公、铁运输企业关系，监管整个联运过程，这样一来，公路运输企业可以专注于干线的配送运输，而铁路运输企业可以更专注于铁路干线运输。公、铁运输企业双方分工更为明确、便于充分发挥各自优势，公、铁运输企业的服务质量更高，无车承运人面向客户的服务质量得到改善，市场份额更大，公铁联运系统的协同程度也更高。在仅有公、铁运输企业参与的集中模式下的协议运量和总利润均大于单一的公路或铁路企业作承运人时的总利润。而无车承运人作市场经营主体时，公、铁运输企业的利润大于公、铁主导的单一模式，充分体现了这种第三方协同模式的优越性。

公路作承运人时，与铁路签订的最优协议运价为42.7元/t，则铁路企业的单位利润为12.8元/t，无车承运人作承运人时与铁路签订的协议运价58.9元/t，铁路企业的单位利润为30元/t，大于12.8元/t。同样的，公路企业的单位利润在无车承运人时更大。这解释了为什么多式联运市场中绝大多数都是无车承运人作承运人，公路或者铁路企业作承运人的情况极少。无车承运人加入其中，增加了整体的利润，协调了公铁的运输，本文中对于公、铁的成本计算较为粗略，实际作承运人面向市场集货成本更大，既要负责揽货，又要负责运输，这对公、铁运输企业来说是一个挑战，极易导致服务质量不高，运输效率低下等问题。无车承运人的加入不仅改进了运输服务的质量，提升了客户满意度，也提高了公、铁的单位利润，更能促进公、铁路运输企业与无车承运人展开联运合作。

6 结论

本文对公铁联运两种决策模式下的公路运输企业、铁路运输企业与无车承运人分别作为运营主体的公铁联运博弈问题进行了研究，主要研究结论如下：

(1) 通过构建博弈模型，得到了集中决策和分散决策下公铁联运物流服务供应链的定价策略、数量决策，得出纵向一体化可以提升系统效率的结论。

(2) 对分散决策下的无车承运人、公路运输企业和铁路运输企业的利润进行比较，分析出三者利益共同体的利益分配模式。

(3) 重点分析无车承运人对于公铁联运系统利益提升的作用，无车承运人通过组织调度公铁运输企业的资源完成运输业务并承担相应风险，可以实现运输链条的利益最大化。最后通过我国朔黄铁路的实际运营数据对博弈模型进行数值仿真。数值仿真的结果表明无车承运人作经营人时，公、铁运输企业的利润要大于单纯公、铁主导模式下的利润，充分体现了无车承运人参与协同模式的优越性。基于上述结论提出以下建议：从促进我国公铁联运物流服务发展的角度，应通过兼并重组等方式使公铁联运参与者形成利益共同体，实现集中控制；在短期不能实现集中决策时，应完善铁路物流中心的经营管理，使其具有促成三方达成收入共享协议并监督协议执行的能力；另外，公铁运输企业应努力降低运输成本，当达到一定的规模时，可以通过规模效应实现成本优势。