考虑阻力约束的列车能量最优驾驶问题建模及分离迭代求解策略

刘良杰，冯江华，王 斌，胡云卿，黎向宇

(中车株洲电力机车研究所有限公司, 湖南 株洲 412001)

轨道交通车辆智能控制已成为当前的研究热点，引起了国内外广大学者的关注并取得了丰硕的成果[1-13]。文献[1]从列车驱动策略节能和运行时刻表节能两方面进行建模，采用Pontryagin极大值原理求解最优控制问题。文献[2]提出了一种两阶段线性规划算法优化地铁列车运行时刻表，通过最小化列车运行过程中的能量消耗以及最大化利用列车制动时的再生能量，可实现节能19.27%以上。文献[3-4]通过对列车运行时刻表进行优化求解实现节能。文献[5-8]根据列车的特性、线路与速度约束等条件建立能量最优控制问题模型进行求解，实现节能。GE公司将列车的能量最优控制问题归结为一个带约束的非线性最优控制问题进行求解，并成功研发了优化节能装置，并在北美内燃机车上应用[5]。西南交通大学冯晓云教授团队借鉴优秀司机的驾驶经验，建立能量最优问题模型，通过Pontryagin极大值原理进行求解[9-10]。北京交通大学徐洪泽教授团队和毛保华教授团队分别建立了列车的节能操作最优控制问题模型，徐洪泽教授团队通过运行区间分段的方法将最优控制问题转化为非线性规划问题[11]；毛保华教授团队通过遗传算法求解节能操作最优控制问题[12]。文献[13]建立了列车运行过程中能量最优的线性二次型最优模型，通过离散化策略将该问题转化为凸二次规划问题进行求解。

本文综合考虑了列车的动力学模型，牵引、制动特性，列车阻力(坡道阻力和运行阻力)，线路限速等条件，在满足安全、准点、平稳的条件下，建立了列车运行过程中的能量最优驾驶问题模型。列车运行过程的动力学方程(不考虑列车阻力)为常微分方程组(Ordinary Differential Equations，ODEs)，由于考虑了列车运行过程中的坡道阻力和运行阻力，列车运行过程的动力学方程增广为微分代数方程组(Differential-Algebraic Equations，DAEs)，使得问题难以求解。为求解该模型，在时间域内将状态变量和控制变量离散化[14-16]，将问题转化为一般非线性规划问题；然后提出了一种分离迭代策略，将该一般非线性规划问题处理为一系列凸二次规划问题，最后采用原-对偶预测校正内点算法求解[17]。

1 列车能量最优驾驶问题

列车运行过程的数学模型为

(1)

式中：t为时间；s(t)为列车的运行距离；v(t)为列车的运行速度；a(t)为列车的运行加速度；F(t)、r[v(t)]、gs[s(t)]分别为作用在列车单位质量上的牵引、制动力，运行阻力，坡道阻力。

r[v(t)]、gs[s(t)]分别为[18]

(2)

式中：α0,α1,α2为列车运行阻力表达式的系数；θ[s(t)]为列车运行过程中的坡道角。θ[s(t)]>0为上坡道，θ[s(t)]=0为平直道，θ[s(t)]<0为下坡道。g为重力加速度常数。

假设列车从A站运行到B站过程中，运行到地点C为t0(t0≥0)时刻，运行到地点D为tf(tf>t0)时刻，运行区间限速值为VLimit，最大加、减速度变化率为aRate(aRate>0)。依据列车的牵引、制动特性，设列车能够达到的最大加速度值为amax，最大减速度值为-amin(amin<0)；设列车的最大牵引力为Fmax，最大电制动力为-Fmin(Fmin<0)，则列车在运行过程中受到的约束条件为

v(t)≤VLimit

(3)

(4)

amin≤a(t)≤amax

(5)

Fmin≤F≤Fmax

(6)

s(t0)=S0v(t0)=V0a(t0)=A0

(7)

s(tf)=S0+S=Sf,v(tf)=Vf,a(tf)=Af

(8)

式中：S0、V0、A0分别为t0时刻列车的运行位置、速度、加速度；S为从t0时刻起至tf时刻列车的运行距离；Sf、Vf、Af为tf时刻列车的运行位置、速度、加速度；t0,S0,V0,A0,tf,Sf,Vf,Af均为已知常数。

a(t)=F(t)-r[v(t)]-gs[s(t)]

r[v(t)]={α0+α1[3.6v(t)]+α2[3.6v(t)]2}×10-3

gs[s(t)]=gsin{θ[s(t)]}≈gθ[s(t)]

s(t0)=S0v(t0)=V0a(t0)=A0

s(tf)=Sfv(tf)=Vfa(tf)=Af

v(t)≤VLimit

amin≤a(t)≤amax

Fmin≤F(t)≤Fmax

(9)

2 离散化策略及问题求解

2.1 离散化策略

对时间区间t∈[t0,tf]进行离散化，等分为N个子时间区间，每个子时间区间的长度为T，则有

(10)

在离散的时间点序列t0,t1,…,tN-1,tN上，对加速度a(t)离散化得到离散的加速度序列a0,a1,…,aN-1,aN；对速度v(t)离散化得到离散的速度序列v0,v1,…,vN-1,vN；对运行距离s(t)离散化得到离散的运行距离序列s0,s1,…,sN-1,sN；对牵引力F(t)离散化得到离散的牵引力序列F0,F1,…,FN-1,FN；对列车的运行阻力r[v(t)]离散化得到离散的运行阻力r(v0),r(v1),…,r(vN-1),r(vN)；对列车的坡道阻力gs[s(t)]离散化得到离散的坡道阻力gs(s0),gs(s1),…,gs(sN-1),gs(sN)。那么，在离散点处的加速度值可表示为

ai=Fi-r(vi)-gs(si)i=0,1,…,N

(11)

在t0和tf时刻，由式(7)、式(8)可得

s0=S0v0=V0a0=A0

(12)

sN=SfvN=VfaN=Af

(13)

(14)

设在[ti-1,ti],i=1,…,N子区间列车的运行距离为Δsi，Δsi可计算为

⋮

i=3,4,…,N

(15)

由于si=si-1+Δsi=S0+Δs1+…+Δsi，可得

i=2,3,…,N

(16)

则式(9)中的等式约束可转化为

a0=A0=F0-r(v0)-gs(s0)

(17)

aN=Af=FN-r(vN)-gs(sN)

(18)

(19)

sN=Sf≈S0+NV0T+

(20)

针对式(9)中的不等式约束，在任意时刻加速度ai需要满足

amin≤Fi-r(vi)-gs(si)≤amaxi=1,…,N-1

(21)

牵引力Fi需要满足：

Fmin≤Fi≤Fmaxi=0,…,N

(22)

aRatei=1,…,N

(23)

限速条件v(t)≤VLimit可转化为

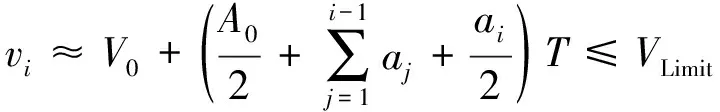
i=1,…,N-1

(24)

式(9)的性能指标函数通过离散化后可近似表示为

(25)

令F=[F0,F1,…,FN]T，式(9)可转化为一般非线性规划问题

s.t.F0-r(v0)-gs(s0)=A0

FN-r(vN)-gs(sN)=Af

Fi-r(vi)-gs(si)≥amini=1,…,N-1

-Fi+r(vi)+gs(si)≥-amaxi=1,…,N-1

Fi≥Fmini=0,1,…,N

-Fi≥-Fmaxi=0,1,…,N

Fi-r(vi)-gs(si)-

[Fi-1-r(vi-1)-gs(si-1)]≥-aRateT

i=1,…,N

Fi-1-r(vi-1)-gs(si-1)-

[Fi-r(vi)-gs(si)]≥-aRateT

i=1,…,N

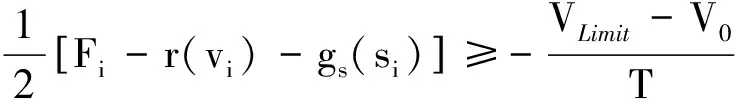
i=1,…,N-1

(26)

在一般非线性规划问题中(式(26))，有N+1个决策变量，4个等式约束，7N-1个不等式约束。

2.2 一般非线性规划问题求解

当不考虑列车的阻力时，式(26)中不包含r(vi),gs(si),i=0,1,…,N，此时式(26)为凸二次规划问题，直接采用原-对偶预测校正内点算法[17]进行求解。当考虑了列车运行过程中的坡道阻力和运行阻力时，式(26)为一般非线性规划问题，增加了求解难度。在式(1)中，r[v(t)]为v(t)的函数，gs[s(t)]为s(t)的函数，不容易直接通过求解式(1)DAEs得到v(t),s(t)表达式，因此，对一般非线性规划问题(式(26))直接进行求解非常困难。可以采用分离迭代策略：令v=[v0,v1,…,vN]T，s=[s0,s1,…,sN]T，假设初始估计值F(0)已知，由式(14)、式(16)可求得v(0),s(0)，代入式(26)中，则问题(26)变为凸二次规划问题，通过求解可得到式(26)的一个近似解F(1)，再由式(14)和式(16)求得v(1),s(1)，代入式(26)继续迭代求解凸二次规划问题。假设迭代求解凸二次规划问题k次后，得到序列{F(k)}，若存在一个充分小的正数ε>0，满足

‖F(k)-F(k-1)‖≤ε

(27)

则终止迭代，由F(k)可求得v(k),s(k)。此时由式(11)、式(14)、式(16)可知F(k-1)≈F(k),v(k-1)≈v(k),s(k-1)≈s(k)，取F(*)=F(k)作为式(26)的一个近似最优解，v(*)=v(k)为近似最优速度曲线，s(*)=s(k)为近似最优运行距离曲线。分离迭代策略的流程图见图1。

图1 分离迭代策略流程图

在分离迭代策略中，将r(vi),gs(si),i=0,1,…,N代入式(26)，则问题可简化为凸二次规划问题，共有N+1个决策变量，4个等式约束，7N-1个不等式约束，其规范化表达式为

s.t.AEx=bE

AIx≥bI

(28)

式中：决策变量x=[F0,F1,…,FN]T∈RN+1；H=2I∈R(N+1)×(N+1)为正定矩阵，I∈R(N+1)×(N+1)为单位矩阵；向量p=0∈RN+1;常数项q=0；AE∈R4×(N+1)，AI∈R(7N-1)×(N+1)分别为等式约束和不等式约束的Jacobi矩阵；bE∈R4,bI∈R7N-1。

针对式(28)，采用原-对偶预测校正内点算法[17]进行求解。对式(28)不等式约束条件添加松弛变量y≥0。令μ∈Rm2≥0为不等式约束y≥0的拉格朗日乘子向量，λ∈Rm1为等式约束AEx=bE的拉格朗日乘子向量。设点z(k)=(x(k),y(k),λ(k),μ(k))为当前迭代点，则下一个迭代点为

(29)

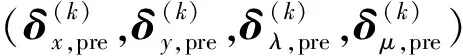
Step1输入相关参数H、p、q、AE、bE、AI、bI,选择初始点(x(0),y(0),λ(0),μ(0))，并设定精度要求tol，令k=0。

Step6计算下一个迭代点为

Step7计算新的对偶间隔

3 算例计算与仿真

假设列车从A站运行到B站过程中，运行到地点C为t0=15 s时刻，在t0时刻列车的加速度A0=0.7 m/s2，速度V0=40 km/h，运行距离S0=100 m；运行到地点D为tf时刻，列车的加速度Af=-0.5 m/s2，速度Vf=5 km/h，运行距离Sf=S+S0=1 900 m；假设列车在运行过程中最大牵引、制动能力为1.0 m/s2，能够允许达到的最大加速度为0.9 m/s2，最大减速度为0.75 m/s2，站间限速值为80 km/h(22.22 m/s)，最大加、减速度变化率为0.75 m/s3。

当不考虑列车运行过程中的阻力时，列车从地点C运行至tf=200 s时刻到地点D过程中的能量最优驾驶问题数学模型为

s.t.F0=0.7

FN=-0.5

Fi≥-0.75i=1,…,N-1

-Fi≥-0.9i=1,…,N-1

Fi≥-1.0i=0,1,…,N

-Fi≥-1.0i=0,1,…,N

Fi-Fi-1≥-0.75Ti=1,…,N

Fi-1-Fi≥-0.75Ti=1,…,N

i=1,…,N-1

(30)

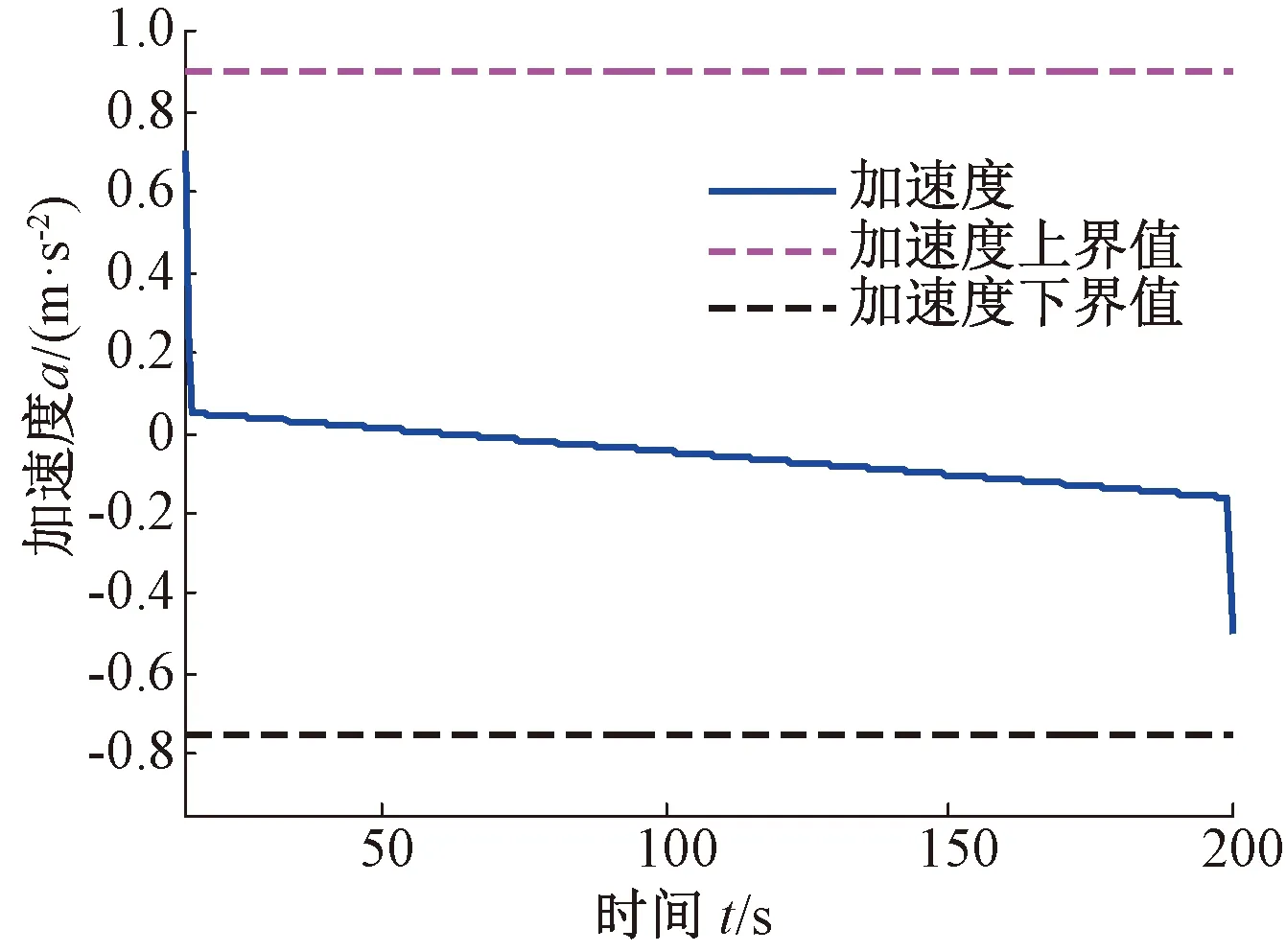
图2 加速度与时间曲线

图3 速度与时间曲线

图4 运行距离与时间曲线

图5 速度与运行距离曲线

图2～图5中，列车从t0=15 s时加速度逐渐减小(大于0)，并在60.6 s时加速度为0，表示该阶段为加速阶段；此后加速度小于0，表示此阶段为制动阶段。加速度大于0时速度不断增加，并在60.6 s时达到最高运行速度12.62 m/s(小于限速值22.22 m/s，在运行时间富裕的情况下列车并非贴限速运行)；加速度小于0时速度不断减小直到制动运行至地点D。运行距离随着运行时间单调上升，且运行到地点D时运行距离恰为Sf=1 900 m。运行速度与运行距离关系呈现出光滑的圆弧形曲线。

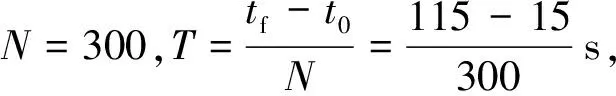
图6 加速度与时间曲线

图7 速度与时间曲线

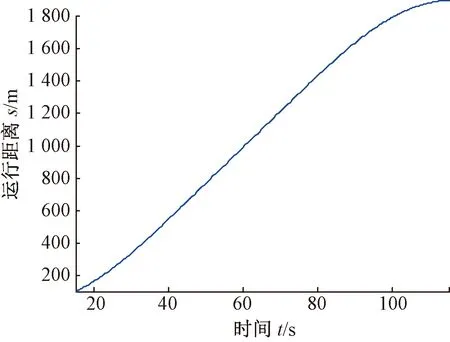
图8 运行距离与时间曲线

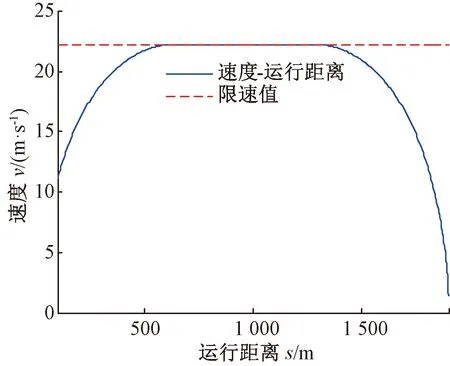
图9 速度与运行距离曲线

图6～图9中，列车在启动阶段的最大加速度为0.76 m/s2(小于允许的最大加速度0.9 m/s2)，表明不需要以最大牵引力起车就能满足运行要求；在44.0 ～72.9 s时间段内加速度为0，表明列车处于惰行阶段(不消耗能量)，随后制动直到运行至地点D，其中在101.7 ～114.6 s时间段内以最大减速度0.75 m/s2减速制动运行。在44.0～72.9 s的惰行时间段内，速度恰为限速值22.22 m/s。运行距离随着运行时间单调上升，且运行到地点D时运行距离恰为Sf=1 900m。运行速度与运行距离关系呈现出光滑的圆弧形曲线。

考虑列车运行过程中的阻力时，假设列车运行过程中的坡道信息为

(31)

列车的运行阻力计算公式为

r[v(t)]=10-3gs{α0+α1[3.6v(t)]+α2[3.6v(t)]2}

α0=0.92α1=0.004 8α2=0.000 125

(32)

列车从地点C运行至tf=115 s时刻到达地点D过程中的能量最优驾驶问题数学模型为

s.t.F0-r(v0)-gs(s0)=0.7

FN-r(vN)-gs(sN)=-0.5

Fi-r(vi)-gs(si)≥-0.75i=1,…,N-1

-Fi+r(vi)+gs(si)≥-0.9i=1,…,N-1

Fi≥-1.0i=0,1,…,N

-Fi≥-1.0i=0,1,…,N

Fi-r(vi)-gs(si)-[Fi-1-r(vi-1)-gs(si-1)]≥

-0.75Ti=1,…,N

Fi-1-r(vi-1)-gs(si-1)-[Fi-r(vi)-gs(si)]≥

-0.75Ti=1,…,N

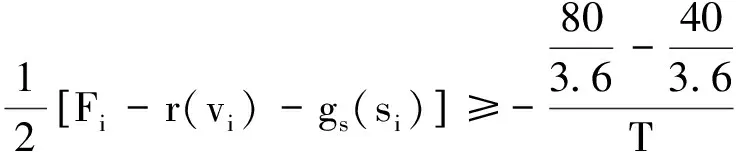
i=1,…,N-1

(33)

图10 加速度与时间曲线

图11 速度与时间曲线

图12 运行距离与时间曲线

图13 速度与运行距离曲线

图14 加速度、牵引力、阻力与运行距离曲线

图10中，列车从t0=15 s时加速度逐渐减小(大于0)直到在47.7 s时加速度为0，表示该阶段为加速阶段；并在47.7～60.0 s时间段内的大部分时间加速度为0(牵引力不为0)；在60.0～69.5 s加速度小于0，列车减速运行；在69.5～77.5 s时间段内由于受到下坡道阻力的影响加速度大于0；此后加速度小于0，表示此阶段为减速制动阶段。图11中，速度不断增加，并在47.7 s时达到限速值22.22 m/s直到60.0 s；在60.0～77.5 s时间内速度先减小后增大(小于限速值22.22 m/s)，此后开始减速制动运行至地点D。图12中，运行距离随着运行时间单调上升，且运行到地点D时运行距离恰为Sf=1 900 m。图13中，运行速度与运行距离关系呈现出光滑的圆弧形曲线。图14中，加速度是由牵引/制动力克服列车运行过程中的阻力后生成；列车在运行区间1 000～1 200 m时(30‰的大上坡道)，以较小的牵引力(小于列车阻力)冲坡运行，同时满足列车运行过程中对速度的要求，因此在该运行区间能够明显体现出节能。

3.2 算法性能分析

在能量最优驾驶问题(式(33))的求解过程中，不断迭代求解凸二次规划问题(式(28))，随着迭代次数的增加，式(28)的最优解将逐渐逼近式(33)的最优解。迭代过程中得到的牵引、制动力与时间，速度与时间，运行距离与时间的曲线见图15～图17。

图15中，迭代过程中的牵引/制动力与时间曲线随着迭代次数的增加逐渐趋近于一条曲线，第3次迭代和第4次迭代得到的牵引/制动力与时间曲线几乎重合，则第4次迭代得到的牵引/制动力为式(33)的近似最优解。图16中，迭代过程中第2次迭代到第4次迭代的速度与时间曲线几乎重合为一条曲线。图17中，迭代过程中的运行距离与时间曲线几乎重合为一条曲线。

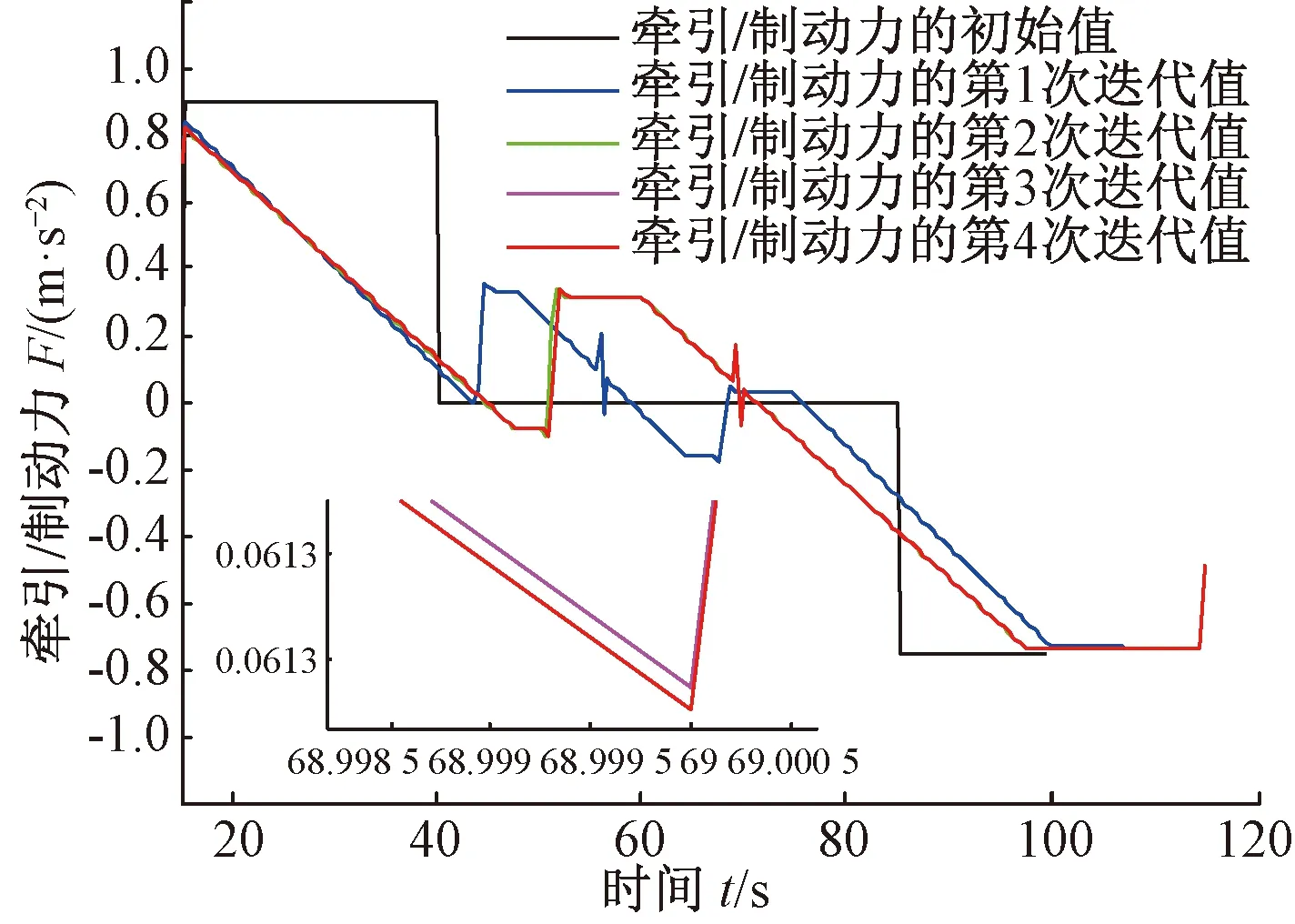
图15 迭代过程中的牵引/制动力(单位质量下)与时间关系

图16 迭代过程中的速度与时间关系

图17 迭代过程中的运行距离与时间关系

4 结束语

本文根据列车的动力学模型，牵引、制动特性，线路限速，列车阻力，乘坐舒适性等约束条件，建立了列车在运行过程中能量最优控制问题的数学模型。由于考虑了列车运行过程中的阻力，约束条件中列车运行过程的动力学方程由ODEs增广为DAEs，使得问题难以求解。为求解该模型，在时间域内将状态变量和控制变量离散化可以将问题转化为非线性规划问题，采用提出的分离迭代策略，可以将该复杂的非线性规划问题转化为凸二次规划问题进行迭代求解。通过对两站间运行的列车能量最优驾驶问题进行求解计算和仿真，验证了所提出方法的有效性。本文考虑的限速值为固定值，后续将进一步研究限速值随线路实际位置变化的复杂情况下能量最优驾驶问题。