A note on the length of conjugacy classes of finite group

XU Xiangyang ,LI Yangming

(1.Department of Mathmetics and Computer Science,Nanchang Normal University,Nanchang 330032,China;2.Department of Mathmetics,Guangdong University of Education,Guangzhou 510310,China)

Abstract：Let a finite group G=AB be the product of the mutually permutable subgroups A and B.We give the structure of G by some conditions on the length of conjugacy classes of elements in A ∪B.Some recent results are extended.

Key Words：mutually permutable product；the length of conjugacy class；p-nilpotent group

0 Introduction

All groups considered in this paper are finite.For an elementxinG,xGdenotes the conjugacy class containingx,and |xG|denotes the length ofxG,that is,the number of elements inxG,we know that|xG|=[G:CG(x)].Furthermore,for any subgroupHofG,xH={xh|h∈H} and |xH|=[H:CH(x)].π(G)denotes the set of prime divisors of |G|,andGpdenotes a Sylowp-subgroup ofG,wherep∈π(G).For an integern,npdenotes the maximalp-power divisor ofn.

The productG=ABof the subgroupsAandBis called a mutually permutable product,ifUB=BUandAV=VAis true for allU≤AandV≤B.The influence of the factors of a mutually permutable product on the structure of the whole group has been extensively investigated in recent years.A detailed collection of such results is given in the book [1].Another interesting question that has also been extensively studied is what we can be said about the structure of groupG,if some arithmetic information is known aboutxGfor some elementsx∈G.There are many papers published recently in literature to answer the question,we mention some of them.By using classification theorem of finite simple groups,CHILLAG et al[2]proved the following results.

Theorem 1([1],proposition 5) LetGbe a group.Ifp=2 andp2does not divide |xG| for anyx∈G,thenGis soluble.

Without using classification theorem of finite simple groups,COSSEY et al[3]generalized the above result.

Theorem 2([2],theorem 1) LetGbe a group andpbe a fixed prime with (p-1,|G|)=1.p2does not divide |xG| for anyx∈G,thenGis a solublepnilpotent group with

LIU et al[4]generalized theorem 2 and got the following results.

Theorem 3([4],theorem 6) LetGbe a group andpbe a fixed prime with (p-1,|G|)=1.Suppose that for everyp'-elementxofG,p2does not divide |xG|.ThenGis a solublep-nilpotent group with

QIAN et al[5]went further to obtain the following result.

Theorem 4([4],theorem A) LetGbe a group andpbe a fixed prime integer such that (p-1,|G|)=1.Suppose that for everyp'-elementxof prime power order inG,p2does not divide |xG|.ThenGis solublepnilpotent,and a Sylowp-subgroup ofG/[Op(G)] is elementary Abelian.

In paper [6],there is an idea to investigate the structure of the mutually permutable productG=ABby giving some conditions on the lengths of conjugacy classes of elements inA∪B,FELIPE,et al[7]followed the way to extend theorem 4.Here we apply different method from [7] to obtain the following result.

Theorem 5LetGbe a group andpbe a fixed prime integer such that (p-1,|G|)=1.Suppose thatG=ABis a mutually permutable product of two subgroupsAandBofG.Suppose that for everyp'-elementxof prime power order inA∪B,p2does not divide |xG|.ThenGis solublep-nilpotent,and a Sylowp-subgroup ofG/[Op(G)]is elementary Abelian.

The following example indicates that theorem 5 extends theorem 4 properly.

Example 1Suppose thatH=〈a,b|a2=b3=1,ba=b-1〉 is a symmetric group of degree 3 andH'=〈a',b'〉 is a copy ofH.DenoteG=H×H'.ThenGsatisfies the hypotheses in theorem 5,wherep=2.Therefore,Gis 2-nilpotent.ButGdoes not satisfy the hypotheses in theorem 4 as 4 divides|(bb')G|.We can not apply theorem 4 to conclude thatGis 2-nilpotent.

1 Lemmas

The proofs in this note rely heavily on results from the book [1].It is one of the best ways to open the book in front of the reader.For the convenience of the difficulty to access to this book,we state the results in this book that we are using.

Lemma 1([1],lemma 4.1.10) Assume thatG=ABis a mutually permutable product of two subgroupsAandBofGand thatNis a normal subgroup ofG.ThenG/Nis a mutually permutable product ofAN/NandBN/N.

Lemma 2([1],lemma 4.3.8) Assume that the groupGis a mutually permutable product of the subgroupsAandB,and thatNis a non-Abelian minimal normal subgroup ofG.Then eitherN≤AorN≤B.

Lemma 3([1],theorem 4.3.11) Assume that the groupGis a mutually permutable product of the subgroupsAandB.ThenAG BGis non-trivial.

Lemma 4([8],lemma 13.6) Suppose thatH/Kis a solublep-chief factor ofG.Then

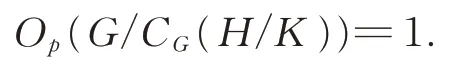
Lemma 5([8],proposition 12.5) Suppose thatQis a π'-group of operators for a Abelian π-group.ThenP=[P,Q] ×CP(Q).

Lemma 6([8],theorem 8.3) Suppose thatGis a nilpotent group andNis a non-trivial normal subgroup ofG.ThenZ(G) ∩Z≠1.

The following facts are well known and we will use them without further reference.

(1) IfNis a subnormal subgroup ofG,then|xN|||xG|for anyx∈G;

(2) Ifx∈GandNis normal inG,then

(3) LetNbe a normal subgroup ofGandpbe a prime.IfxNis ap-element ofG/N,then there is ap-elementx1ofGsuch thatxN=x1N.

2 Proof of theorem 5

We firstly prove thatGis solublep-nilpotent.Assume that it is false and chooseGto be a counter example of minimal order.We will reach a contradiction in several steps.

Step 1Ghas an unique minimal normal subgroup,Nsay,andG/Nis solublep-nilpotent,andΦ(G)=1.

Pick a minimal normal subgroup ofG,Nsay.

By lemma 1,the hypotheses are inherited into quotient groups.HenceG/Nis soluble andp-nilpotent by the minimal choice ofG.This implies thatNis the unique minimal normal subgroup ofG.

IfΦ(G) ≠1,then we haveN≤Φ(G).And then we haveGis solublep-nilpotent,a contradiction.

Step 2Gis soluble.HenceNis an elementary Abelianp-group.Furthermore,Nis complemented inG,byHsay,andCG(N)=N.

Assume thatNis non-Abelian.Then,by lemma 2,we haveN≤AorN≤B.SoNsatisfies the hypotheses of theorem 4.ThusNis soluble,a contradiction.ThusNis an elementary Abelianp-group andGis soluble.

SinceN≰Φ(G)=1,there exists a maximal subgroup ofG,Hsay,such thatG=NH.SinceN∩His normal inG,we haveN∩H=1,i.e.,Nis complemented inGbyH.

SinceCH(N)is normal inG,we haveCH(N)=1.ThenCG(N)=NCH(N)=N.

Hence step 2 holds.

Step 3Pick a minimal normal subgroupMofH.We can assume thatMN≤ANandM≤Agfor someg∈G.

We haveMN/Nis a minimal normal subgroup ofG/N=G/CG(N).SoMN/N≅Mis an elementary Abelianq-group by lemma 4,whereqis a prime distinct withp.By lemma 1,G/Nis a mutually permutable product ofAN/NandBN/N.So we can assume thatMN/≤AN/Nby lemma 3.

SinceNis ap-group,the Sylowq-subgroupAqofAis a Sylowq-subgroup ofAN.HenceM≤Agfor someg∈Gby the famous Sylow theorem.

Step 4The final contradiction.Pick a non-trivial elementm∈M.RegardNas an 〈m〉-module.By Maschke theorem ([8],theorem A.11.4),we can write

whereNiis an irreducible 〈m〉-module fori=1,2,…,t.Since (p-1,|G|)=1,we have thatq†p-1.Then |Ni|≥p2for anyiby [8],theorem B.9.8 (d).

By step 2,m∉CG(N)=N.Hence there exists at least oneNisuch thatmdoes not centralize it,N1say.Hence [m,N1]=N1.SoCN1(m)=1 by lemma 5.This implies that |mN1|=[N1:CN1(m)|=|N1|≥p2.Sop2||mN1|.Thenp2||mG|.

By step 3,some conjugatexofmis inA.Hence we have |xG|=|mG|andp2||xG|,the final contradiction.

HenceGis soluble andp-nilpotent.

LetGpbe a Sylowp-subgroup ofG.We show thatGp/Op(G) is elementary Abelian.By standard arguments and induction,we can assume thatOp(G)=1 andΦ(G)=1.

By lemma 3,we pick a minimal normal subgroupLofGcontained inAorB.ThenLis an elementary Abelianq-group,whereqis a prime distinct withp,andLis complemented inGasL≰Φ(G)=1.We may writeG=LMandN≰L∩M=1.By lemma 1 and induction,we haveMp/Op(M)is elementary Abelian.

IfOp(M)=1,then by inductionMp=Gpis elementary Abelian,as wanted.Thus assume thatOp(M) ≥1.

Pick a non-trivial elementxinL.Noticing that|xG|=[G:CG(x)| is not divisible byp2by hypotheses,CMp(x) contains a maximal subgroup ofMp.In particular,CMp(x) is normal inMp.HenceCMp(x)∩Mpis normal inMp.IfCMp(x)∩Mp≠1,thenOp(M) ∩CMp(x)∩Z(Mp) ≠1 by lemma 6.LetZbe a minimal subgroup ofOp(M) ∩CMp(x)∩Z(Mp).SinceMisp-nilpotent,Op(M)∩Z(Mp)≤Z(M).ThusZ≤Z(M).SinceG=LM,CL(Z) is normal inG.ThenCL(Z)=1 orCL(Z)=Lby the minimality ofL.IfCL(Z)=L,thenZ≤Z(G) andZ≤Op(G)=1,a contradiction.HenceCL(Z)=1.This implies thatxdoes not centralizeZ.HenceZ≰CMp(x),contrary to the choice ofZ.HenceCMp(x)∩Op(M)=1.ThenMp=CMp(x)Op(M)=CMp(x)×Op(M).This also means thatCMp(x) is a maximal subgroup ofMpandOp(M) is of orderp.Since

CMp(x) is elementary Abelian.Then we have thatMp=CMp(x) ×Op(M)is elementary Abelian.

This completes the proof of the theorem.