基于规则学习的传统纹样统一生成模式研究

李华飙，侯小刚，王婷婷，赵海英

（1.中国国家博物馆数据管理与分析中心，北京 100006；2.北京邮电大学计算机学院（国家示范性软件学院），北京 100876）

0 引言

为表达对自然现象等场景的崇拜之情，祖先们绘制了许多不同的图腾，传统纹样亦应运而生。在现代社会中，传统纹样主要用于装饰。本文选取几何纹、动物纹、植物纹三大类传统纹样对其生成方法进行研究，旨在对传统纹样进行原真保护、传承和应用。纹样作为我国传统文化的重要组成元素，研究其生成方法有利于对传统文化的保护。

早期对传统纹样的研究主要集中于演变规律及文化传播的影响，研究者大多为人文学者或设计师。计算机的诞生和发展，特别是Photoshop、AutoCAD等软件的出现，为广大设计师提供了极大的便利。同时，计算机图形学（computer graphics）得到了快速发展，纹理生成作为图形学的重要研究方向，广受关注，目前已有多种较好的纹理生成算法，如对原始纹理进行重采样生成［1］、定义参数化纹理模型［2］等。随着深度学习的发展，已出现用于生成多种纹理的深度模型，如卷积神经网络［3］等。

上述生成算法面向的是物体表面的纹理，而对于在物体表面上的纹样生成，研究较少，且局限于特定的较为著名的纹样，如Islamic、Kolam 等纹样。Islamic 纹样的生成方法主要有群论法［4］、图元法［5］等；Kolam 纹样的生成方法主要有图论法［6］、块方法［7］等。通过分析前人工作发现，已有算法主要针对某一类特定纹样，对其他类别传统纹样并不适用。笔者通过分析不同种类纹样的生成方法，基于纹样的异同点得到传统纹样的统一生成模式。利用计算机及相应算法生成传统纹样，可为设计师提供广泛的纹样素材，更好地传承和利用中华传统文化。

1 传统纹样的特征分析

由于传统纹样具有可量化的特征，本文分别选取几何纹、植物纹、动物纹中较为典型的纹样进行量化特征分析。

1.1 几何纹样的特征分析

几何纹是最早出现的传统装饰纹样，5 000 年前的新石器时代就已广泛将几何纹用于彩陶装饰。各种直线、曲线，及圆形、三角形、方形、菱形等构成规则或不规则的几何图形，这些几何图形均可认为是几何纹样。常见的规则几何纹样主要有Islamic 纹样、Kolam 纹样、回纹、云纹等。

Islamic 纹样在几何纹中最为经典，它将几何的运用推向了极致，具有极高的艺术造诣。文献［9］给出了其基本构成特点：（1）基本构成形体为单纯的多边形，（2）重复平铺展开，（3）线条明显，在线条相交处往往用上下重叠的方式进行处理，以加强线条感与立体感。Kolam 纹样是妇人用米磨成的粉画的花鸟星辰等精美吉祥图案，是印度南部TamilNadu 邦最具代表性的民间艺术之一。回纹和云纹是我国民间常用的传统纹样，回纹是由横竖短线折绕组成的方形或圆形的回环状花纹，在民间有“富贵不断头”的美好寓意。云纹是对云形状的模拟，有高升和如意的美好寓意。

本文以Islamic 纹样为例，进行几何纹特征分析。文献［9］采用参数化形状语法生成了Islamic 纹样，如图1（a）所示。

由图1 知，完整纹样（图1（a）），主要由基本形状单元（图1（b）红线所示）及经轴对称与中心对称复制操作得到的所有中心线组成，基本形状单元由4 条线段连接而成。其中，线段P1P2与P1P3（见图1（c）中红色与绿色标识）的起点均为P1，P1为在外接圆半径为r的正六边形边上距离端点为D的点，P1P2和P1P3与P1所在边的夹角均为α，以保证在重复平铺后与相邻的线段重合为一条新的线段。P1P2和P1P3的长度分别 为L1和L2。另2 条线段 为P2P4和P3P5，在 图1（c）中，分别用黄色和蓝色标示。点P4和P5是点O到边的垂线OP6上的点，P4，P5与O的距离 分别为L4和L3，可通过修改参数D、α、L1、L2、L3、L4得到新的基元图案。

图1 Islamic 纹样特征分析Fig.1 Analysis on the features of the Islamic patterns

1.2 动物纹样的特征分析

我国传统动物纹最早可追溯至原始社会时期，其表达了祖先对自然界中动物、植物以及自然现象的崇拜。传统动物纹主要有2 种：一种是怪兽纹，如饕餮纹、龙纹、凤纹等，这类动物在现实世界中并不存在；另一种是现实世界中真实存在的动物的纹样，如牛纹、马纹、羊纹等。我国传统动物纹主要用于装饰陶器、青铜器、刺绣、玉器、漆器、金银器、建筑物等，对现代人的生活、思想与创作均有一定影响。

本文以剪纸动物纹为例，分析传统动物纹的生成规则。对于剪纸动物纹，文献［10］从构造不同细节区域出发，利用不同参数控制生成样条曲线，进而组合成纹样，实现计算机辅助生成剪纸形象；文献［11］设计了生成剪纸的CAD 系统，构建了剪纸基本元素数据库、剪纸常用符号数据库、剪纸图像数据库，只要分别从各个数据库中选取相应元素便可组合成完整纹样。

首先，选取一张剪纸动物纹，见图2（a）。对图2（a）进行分析知，其包含不同的基本形状单元，见图2（b）。对不同基本形状单元进行拆分、合并，发现其由不同的纹样元素构成，见图2（c）。通过相应方法重新生成纹样基元，进而实现整张图案的创新生成。

图2 剪纸动物纹特征分析Fig.2 Analysis on the features of Chinese paper cut-out of animal figures

1.3 植物纹样的特征分析

从原始社会到商周时期，动物纹和几何纹装饰平分天下，到魏晋南北朝前，植物纹只起陪衬作用，数量较少，而在魏晋南北朝后，植物纹开始流行，与动物纹和几何纹平分秋色，至唐朝后期，植物纹已成为装饰艺术的主流，在建筑、陶瓷、金银器、漆器、丝绸等领域得到广泛应用。

植物纹主要的表现形式有花卉、树与叶、果实、卷草等。本文选取较具代表性的植物纹——宝相纹进行规则分析。宝相纹是以莲花或牡丹为母体经艺术加工得到的一种花纹，具有美满的寓意，极富装饰美。宝相纹的基本结构是偏心圆，以内圆作略带透视的花蕊，外圆通过圆心的垂直中轴作左右对称的花瓣，并将云头造型与花瓣造型结合，组合成宝相纹，如图3（a）所示。

分析宝相纹结构发现，其为左右对称结构，并且可分为几个不同的基本形状单元，如图3（b）所示。在基本形状单元的基础上，继续对宝相纹进行分析，发现这些基本形状单元由一些更小的基元经平移、旋转、缩放等变换组合而成，对其进一步分解、合并，得到如图3（c）所示的宝相纹基元，即宝相纹的最基本组成单元。通过对基元图案进行线条拟合，得到相应的矢量化图案，对其进行调整，从而实现宝相纹的计算机生成。

图3 宝相纹特征分析Fig.3 Analysis on the features of the designs of composite flowers

1.4 传统纹样的特征分析

我国的传统纹样历史悠久，蕴含丰富的文化内涵，广受设计师青睐。而如何将传统纹样应用于现代设计也是设计师们需要思考的问题，图4［8］展示了设计师在创作过程中以手工方式绘制的3 张传统纹样及其详细绘制流程。

图4 纹样手绘过程图Fig.4 Hand drawing of patterns

图4（a）～（c）自左至右分别展示的是3 个纹样的手工绘制过程，即纹样的生成规则。观察图4 中最右侧一列纹样发现，每个纹样都有其生成元素（图中红线框选中部分），即纹样基元，旋转纹样基元可得到最右侧纹样图，从而达到对纹样进行量化的目的。因此，传统纹样可量化的条件是具有纹样基元或（和）具有一定的生成规则。

在对传统纹样进行量化基础上，可提取纹样中的文化基因，即在特定地域和民族文化环境中形成的具有稳定性和继承性的基本信息模式。通过分析某类纹样中不同形式的文化基因，找寻纹样蕴涵的时代背景及文化。以卷草纹为例（见图5），在魏晋南北朝时期，局势动乱，长期的战争导致国家分裂，而正是由于北方游牧民族和西域文化的碰撞，此时期的纹样较丰富，卷草纹也随着忍冬纹和佛教文化的传入开始萌芽；而在包容共济的隋唐时期，由于受外来文化的深刻影响，出现了各种形式的卷草纹，此时纹样处于鼎盛时期。

在欧洲，卷草纹寓意复活、重生；在阿拉伯地区，卷草纹寓意宇宙的浩瀚辽阔；在中国和日本，卷草纹的含义来自藤蔓连接的花卉，突出的是与自然和谐共生，有祥云自如流转和佛教轮回的象征，其无限重复的造型表达了生生不息的生长之气。

图5 基于规则学习的卷草纹生成模式Fig.5 Patterns generation model of the scroll design based on rule learning

2 基于规则的传统纹样统一生成模式

通过分析典型的传统几何纹、动物纹、植物纹的特征，发现其生成规则较为相似，总结其异同点，可归结传统纹样的统一生成模式。

无论是几何纹、植物纹还是动物纹，都由相应的基本元素构成，即组成纹样的、无明确文化寓意的基本单位。可以通过曲线拟合或公式计算等方式生成，进而通过调节相应参数，生成不同形状的元素；在不同形状元素生成基础上，对其进行旋转、平移、缩放等变换，生成相应的基本形状单元，即具有一定寓意的纹样基元；纹样基元之间通过自适应填充、融合等合成完整的纹样。本文所构建的传统纹样统一生成模式是一种具有层次的，且层次越高寓意越完整的图案生成模式（如图6 所示）。

2.1 纹样元素提取

按照基元形状的复杂度，采取不同的方式提取传统纹样基元。当基元为不规则曲线时，可采用公式进行曲线拟合，当基元为简单图形时，可通过相应公式生成；当基元形状较复杂，无对应公式时，可采用参数化形状语法生成；当基元形状很复杂，无法用上述方法生成时，可采用分割法从原图中提取。

2.1.1 公式生成

对于不规则曲线，可通过曲线公式进行拟合，其中用于拟合的曲线主要有Bezier曲线、B 样条曲线等。

对于Bezier 曲线，一般选取三次Bezier 曲线，公式为

其中，P0，P1，P2，P3分别表示三次Bezier 曲线的4 个控制点，P0，P3分别为曲线段的起点和终点，t为控制参数。通过调节控制点进而生成更复杂的线条。

对于B 样条曲线，公式为

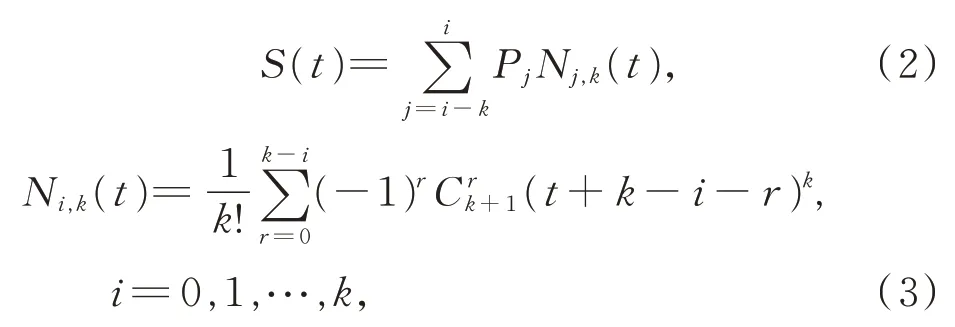
其中，S（t）是控制点与基函数的乘积之和，从点Pj到点Pi，共有（i－j＋1）个控制点，Ni，k（t）为基函数，k表示k次B 样条曲线。由于k次B 样条曲线的控制点有k＋1 个，其局部性较Bezier 曲线更良。

另外，对形状较为简单的，如圆或椭圆等，可通过公式生成。式（4）为圆的生成公式，式（5）为椭圆的生成公式。

其中，（a，b）为圆心坐标，r为圆半径，（h，k）为椭圆心坐标，a、b分别为椭圆的长轴和短轴。通过给定相关参数，可以确定一个圆或椭圆的基本形状。

2.1.2 形状语法生成

对于无法用公式表示的形状较为复杂的基元，可采用形状语法生成。形状语法由STINY 等［12］于1972 年提出，现已被广泛应用于数字化设计等领域。形状语法可用四元组SG（S，L，R，I）表示，其中，S是一个有限的形状集合；L是一个有限的标记集合；R是有限的形状规则组合；I是初始标记形状。首先，给出相应的初始形状和文法规则，然后，通过调节相关参数得到丰富的图案。

2.1.3 分割提取

当图案中的基元很复杂，无法通过上述方式得到时，可通过分割法从原图案中提取相应基元。传统分割法有阈值片［13］、边缘片［14］等。随着深度学习的迅速发展，已有许多优秀的模型和算法，可得到更精确的分割物体，如DeepLab［15］、Mask-RCNN［16］等算法。通过相关分割算法对图案进行分割，提取相应的基元，供后续应用。

2.2 纹样基元构成

通过平移、旋转、缩放，对不同纹样基元进行变换，得到相应纹样的基本形状单元。

平移，主要指图像在x和y方向上进行移动，假设图像上某点向x方向移动dx，向y方向移动dy，［x，y］为移动前坐标，［X，Y］为移动后坐标，则

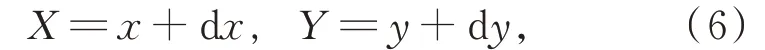
用矩阵表示：

旋转，主要指图像以原点为中心，沿某个方向旋转一定角度。假设某点与原点的连线与x轴的夹角为b°，以原点为圆心，逆时针旋转a°，原点与该点的连线长度为R，［x，y］为旋转前坐标，［X，Y］为旋转后坐标，则

用矩阵表示：

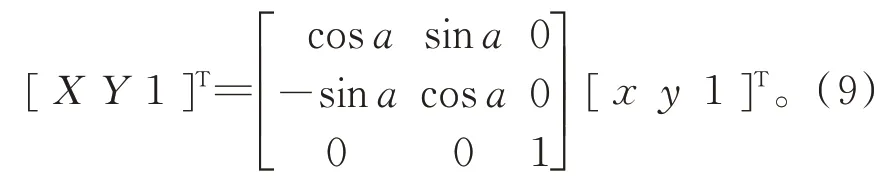
缩放，主要指图像按照一定倍数进行放大或缩小。假设图像上某点在x轴方向扩大sx倍，在y轴方向扩大sy倍，［x，y］为缩放前坐标，［X，Y］为缩放后坐标，则

用矩阵表示：

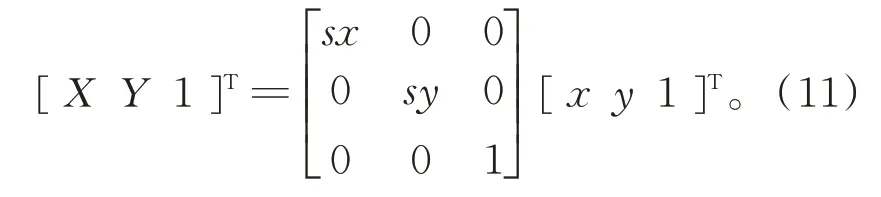
2.3 纹样图案合成

对于生成的不同纹样基本形状单元，可通过不同方式合成传统纹样图案，采用填充方式，确定图案边界及初始纹样，通过自适应方式将其他辅纹添加到空白区域，取得和谐美观的效果［17］。

2.3.1 元素放置算法

在给定区域何处放置元素、放置何种元素，使生成的纹样更符合大众的审美观，FUCHS 等［18］总结了4 种不同的元素放置方法。

（1）模板算法，输入由用户定义的模板放置元素，在二进制模板中，值为1 的位置为可填充区域，可填充所需元素，值为0 的位置为非填充区域，需要留白。也可将二进制模板变换为多进制模板，模板中，不同值区放置不同的元素，从而增强生成纹样的多样性。

（2）对称算法，在已知前一个元素放置位置(x，y)的前提下，该算法倾向于将当前元素放置在与前一个元素构成镜像对称或旋转对称的位置；若这样的位置无法放置（如对称位置已放置元素），则可将当前元素放置在允许未来元素放置在对称位置而不与现有元素冲突的位置；排除太靠近现有元素的位置以及边界之外的位置。

（3）路径算法，选择最长的流线作为路径或从给定种子点开始进行装饰纹样生成，将元素放置在跟踪的流线上，与用户指定的路径相同，重复寻找下一个最长流线或下一个种子点，继续进行元素放置，不断迭代直至填充完装饰空间。

（4）图像数据算法，该算法由艺术家指定样本图像，根据样本图像的亮度确定放置位置的优先级，并以此进行元素选择。

2.3.2 自适应填充算法

自适应填充算法包括图像二值化、二值图像距离变换、区域填充三部分。

Step1图像二值化。

图像二值化技术已很成熟，在很多图像处理工具中都集成了相应的函数。

Step2二值图像距离变换。

距离变换（distance transform）即将包含目标像素（前景）和非目标像素（背景）的二值图像转换为相应的灰度图像，其中，灰度图像中每个像素的亮度值与其和背景的最小距离有关，最小距离由所选距离函数计算得到。距离变换公式为

其中，D为二值图像I的距离图，p为目标集中的点，q为背景集中的点，disf()为距离函数。

Step3区域填充。

以step2 中得到的距离图为指导，进行区域填充。首先，找到距离图中亮度值最大的点，将其作为代理圆的圆心，根据用户定义的初始半径绘制初始代理圆。在与已有元素和边界不相交的情况下，不断增大代理圆的半径，直至相交，完成此点处最大代理圆绘制。

3 统一生成模式应用示例

由上文总结得到的传统纹样统一生成模式分别生成相应的几何纹、动物纹和植物纹。

3.1 几何纹生成示例

回纹是一种重要的传统几何纹样。文献［19］对方回单行体型、减笔组合型、正反“～”型、一笔环连型4 类回纹进行了分析和概括，此4 类回纹的造型如图7 所示。

图7 回纹样例Fig.7 Examples of meander patterns

以图7（b）所示的减笔组合型纹样为例，用所构建的传统纹样统一生成模式生成回纹，其生成流程如图8 所示。

3.2 动物纹生成示例

以图9 红线框中的猫头鹰纹为例，用传统纹样统一生成模式生成猫头鹰纹，其生成流程如图10所示。

3.3 植物纹生成示例

选取卷草纹作为植物纹样例，卷草纹有着丰富的变换形态，图11 为北魏的忍纹边饰（莫高窟第257窟两种《敦煌图案集》第3 页）［20］。用传统纹样统一生成模式生成卷草纹，其生成流程如图12 所示。

图8 回纹生成流程Fig.8 Illustration of meander pattern generation process

图9 动物纹样例Fig.9 Example of animal patterns

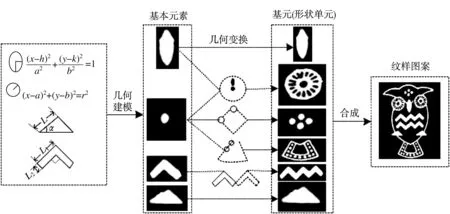
图10 猫头鹰纹生成流程Fig.10 Illustration of the owl pattern generation process

图11 卷草纹样例Fig.11 Example of the scroll patterns

4 总结

图12 卷草纹生成流程Fig.12 Illustration of the scroll pattern generation process

现有的纹样生成方法主要针对某一类特定纹样，泛化能力较弱，笔者通过观察大量传统纹样，找到其共性，即可量化的传统纹样需要具有纹样基元或（和）具有一定的生成规则。本文选取几何纹、动物纹、植物纹为研究对象，比较这些纹样的异同点，提出逐层显现寓意的传统纹样统一生成模式，从而实现对不同种类传统纹样进行原真建模和创新生成，以更好地对传统纹样进行原真保护和创新应用。