一类高阶非线性非自治动态方程的动力学性质

张萍，杨甲山

（1.邵阳学院 理学院,湖南 邵阳 422004；2.梧州学院 大数据与软件工程学院,广西 梧州 543002）

0 引言

振动（亦称振荡）是一种常见的物理现象，广泛存在于自然界和工程技术的各个领域，如机械振动、同步加速器中波束的振动、化学反应过程中的复杂振动以及自动控制系统中的自激振动等，这些振动现象可以统一为系统的振动理论。急动度［1］（亦称加加速度）是描述机械运动的重要基本概念，常用于物理学的混沌理论和非线性动力学、高层建筑的抗风抗震设计以及交通工具设计等。急动度是加速度对时间的变化率，为三阶微分方程。近年来，微分差分方程的“统一、推广形式”——时间测度链上动态方程的有关理论的研究取得了重要进展［2-17］，但大多是对一阶和二阶动态方程的研究［4-7，16-17］，对三阶及三阶以上高阶动态方程的研究相对较少［8-15］。本文研究时间测度链T 上一类非线性非自治高阶动态方程：

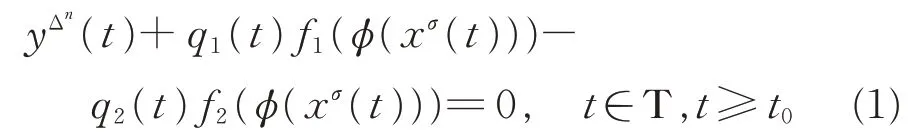
的振动性，其中，y(t)=x(t)+p(t)g(x(t))，φ(u)=|u|λ-1u，实数λ＞0，而n≥3 为整数，并且下 列条件成立：

（H1）T 是任意时间测度链，且sup T=+∞；对t0∈T 且t0＞0，定义时间测度链区间[t0，+∞)T=[t0，+∞)∩T。

（H2）函数p，qi∈Crd(T，R)，且p(t)≥0，qi(t)≥0，i=1，2（下同，略）。

（H3）函数g，fi∈C(R，R)，且ug(u)＞0(u≠0)，ufi(u)＞0(u≠0)，当u≠0 时，g(u)/u≤η，f1(u)/u≥L1，f2(u)/u≤L2，且L1q1(t)-L2q2(t)＞0，其中，0 ＜η≤1 和Li＞0 均为常数。

系统（1）的解及其振动的定义可参看文献［2-15］。时间测度链T 的理论及其微积分的一般知识，可参看文献［2-3］。本文的目的是在无0≤p(t)＜1条件限制下建立n（n≥3）阶非线性非自治动态方程（1）振动的若干准则，得到的振动准则改进了现有的结论。在相应的高阶非线性非自治微分方程和差分方程中，此振动准则也是新的。

1 引 理

2 主要结果及证明