弯曲型聚吡咯驱动器的驱动特性及其建模研究

习爽 左双双

摘 要 基于自主搭建的测试平台，研究层状弯曲型聚吡咯驱动器的电化学-机械特性。根据驱动器的结构特点和工作原理，将其等效为悬臂梁进行建模，将驱动器内部的离子迁移产生的力等效为施加在悬臂梁上的载荷，构建驱动器的弯曲模型。选取3种不同长度尺寸的驱动器，对其施加低电压，测量其在不同电压下的顶端位移。将测量数据带入上述弯曲模型，得出电压与驱动器的顶端位移、曲率半径、弯矩、应变之间的函数关系，基于实验结果验证模型的准确性。此模型可拟合出驱动器的基本参数，准确预测实际运用中的变形行为，从而提高研究的效率。本研究可为聚吡咯驱动器应用于实际系统提供制备、系统建模方面的实验和理论依据，进而推动微型驱动器在微纳米操纵、溶液微粒分析、生物传感等领域的应用。

关键词 聚吡咯; 驱动器; 弯曲模型; 电化学-机械特性

1 引 言

电活性聚合物在人工肌肉和传感器领域具有良好的应用前景，因此引起了广泛关注[1，2]。聚吡咯（PPy）是一种重要的电活性聚合物，具有良好的生物兼容性和生物可降解性，制备简单，驱动耗能低，在液体和空气环境中均能工作，且在体积变化较大时仍能保持稳定[3，4]，常应用于电化学-机械驱动器领域，包括微型阀门[5]、微型泵[6]、流体处理设备[7]、传感器[8]以及微纳操纵器[9]。 PPy具有体积变化大、稳定性高等特点， 尤其适用于电活性驱动器的应用。基于PPy的电活性驱动器称为PPy驱动器，其工作机理是离子在电化学反应中的迁入/迁出引起体积的膨胀/收缩[10]。当聚合物电化学掺杂时，离子被送入聚合物中，导致体积膨胀，反之体积收缩。PPy驱动器根据结构不同可分为两大类：独立膜线性驱动器和叠层弯曲驱动器[11～14]，其中，叠层弯曲驱动器通常由介质层和聚合物层叠加组成，由于介质层可储存氧化还原反应所需的离子液，此种类型驱动器可在空气中运行。施加低至1 V的电压，引起PPy的体积变化，由此引起叠层弯曲驱动器的弯曲变形，这表明电化学能转化为机械能。PPy驱动器具有高可逆性和安全性（低电压），产生的机械应力大，可能的最大应变值大[15]，在驱动方面具有独特的优势。

目前，研究者已针对PPy驱动器的制备工艺进行了大量研究工作，文献已报道了不同类型的驱动器制备方法。然而，尚缺乏针对PPy驱动器工作机理与传感应用建立准确有效模型方面的研究报道，需要更加深入的理论研究， 以阐明影响驱动器动态位移的机理。Santa等[16]使用两种方法构建电化学-机械模型，研究了PPy独立膜线性驱动器在不同负载下的有效位移和尖端力。这是一个简单的集总参数模型，其参数通过力和长度数据的变化识别[17]。Nemat-Nasser[18]制备了Nafion膜-贵金属薄膜双层复合驱动器，通过建立微机械弯曲运动模型探索驱动器的电化学-机械响应。通过测试Nafion-贵金属复合结构和裸Nafion膜在不同条件下的刚度参数，建立内应力与由其产生的刚度和驱动器变形之间的关系，从而探索引起材料机电转换行为的潜在微观机制，基于微观力学理论对其进行建模，并将模型结果与实验数据进行比较，验证了模型的有效性。Nguyen等[19]綜合考虑扩散阻抗、双层电容、导电聚合物电阻和电荷转移电阻，构建了电活性聚合物驱动器通用模型，用于描述离子扩散、电荷转移的电容和电阻，利用非线性最小二乘估计方法从实验结果中得出模型参数。

由于PPy驱动器的变形行为涉及到电化学过程，无法对其弯曲变形行为直接进行建模，由此导致叠层弯曲驱动器至今仍缺乏有效的电化学-机械转换模型，从而无法准确预测PPy驱动器的形变。本研究制备了层状弯曲型PPy驱动器，根据PPy驱动器的结构及工作机理，将弯曲型驱动器等效成悬臂梁进行研究。结合实验中材料的固有参数和驱动器尺寸，开发了一种简单实用的方法描述驱动器的弯曲行为，并采用实验数据验证了此模型的准确性。

2 实验部分

2.1 驱动器的结构及工作原理

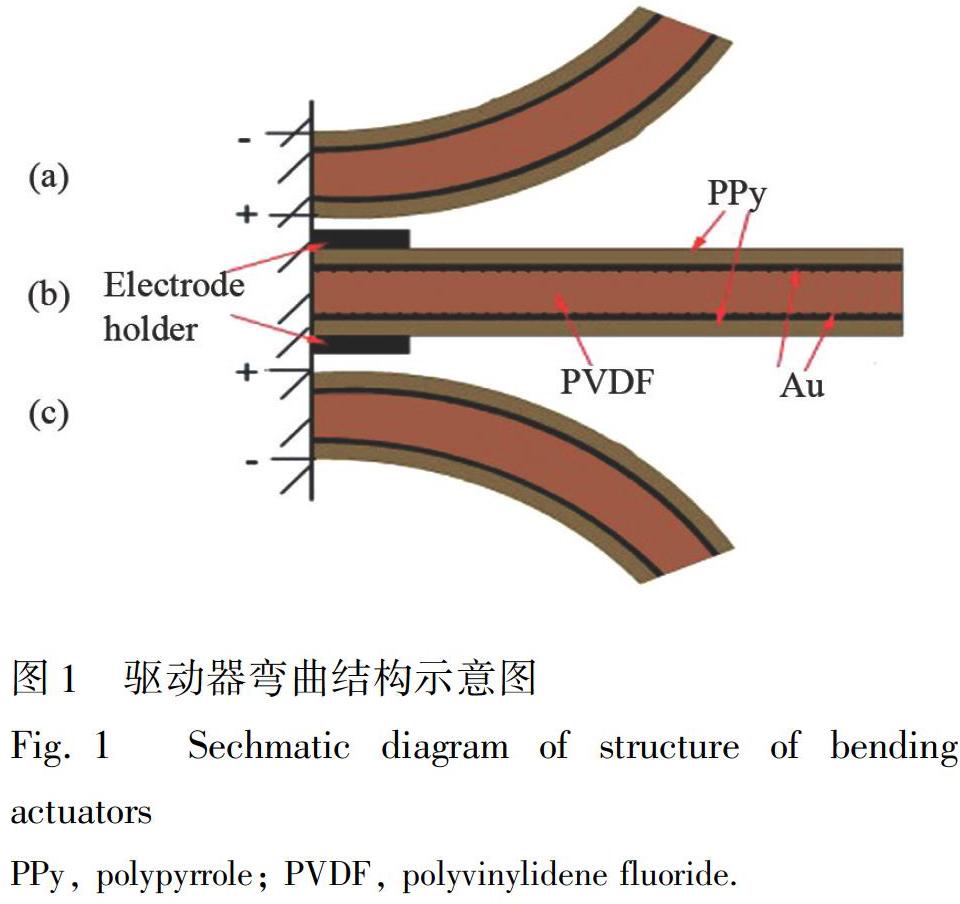
弯曲型PPy驱动器有五层结构，分别为PPy、金、聚偏氟乙烯（PVDF）、金、PPy，如图1b所示。PVDF作为驱动器中间层（厚度约为110 μm），用以隔离最外侧的两层PPy膜，还可用于储存离子液，使得驱动器能够脱离液体环境， 在空气中稳定工作。在PVDF膜的两侧镀金（厚度约为50 nm），以提高表面导电性，便于PPy的电化学沉积。PPy是驱动器的最外两层薄膜，厚度约为30 μm，与电极的正负极接触，是提供驱动的电活性元件。由于金层是纳米级，在PPy和PVDF之间并未形成连续的膜，因此离子可通过，以保证PVDF中存储的离子液可到达PPy层。本研究选用二三氟甲基磺酞阴离子（TFSI）作为离子液，离子液的配制方法及PPy驱动器的制备方法本研究组前期已进行了报道[10]。

当外加电位时，PPy层会发生氧化还原反应，化学过程表示如下：

从电解质中迁移到带正电荷的PPy层，导致正极体积膨胀; 而TFSI离开负极， 导致此侧PPy层收缩，总的结果是驱动器结构将向负极/阴极弯曲，如图1a和1c所示，变换正负极即可使驱动器往复摆动。

2.2 实验测试平台

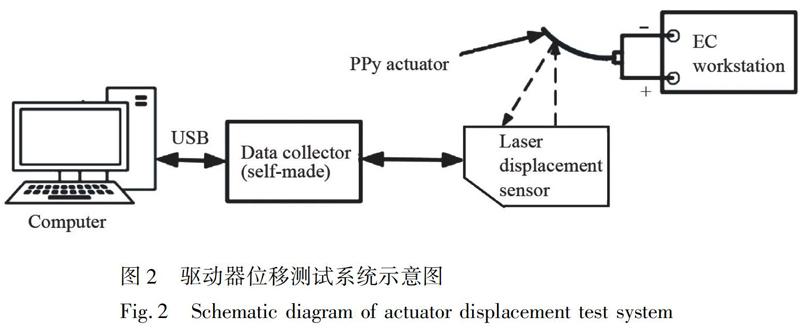
PPy驱动器自由端的偏转位移测试实验是通过对驱动器施加恒电压，然后测试其自由端的弯曲变形进行的，通过测量不同尺寸的驱动器在0 ～1.0 V电压下的弯曲变形量，研究输入电压与偏转位移的关系。驱动器位移测试平台的主要测试设备包括：微型激光传感器（HG-C1050，日本松下电器公司）、数据采集器（自制）、CHI660E电化学工作站（上海辰华公司）、测量显微镜BC1800（三代，广东博晟电子公司）。自制的数据采集器一端连接激光位移传感器，另一端连接电脑，可将数据传入电脑，直接在电脑上输出位移值，位移精度为0.001 mm。CHI660E电化学工作站在位移测试实验中作为恒电位仪使用。位移测试系统示意图如图2所示。

3 结果与讨论

3.1 驱动器的弯曲运动建模

在进行位移测试时，驱动器一端固定在电极夹上，另一端不受力，即为自由端，因此，可将驱动器等效为悬臂梁进行分析建模。基于小变形假设，并且忽略极薄的金层影响，建立PPy驱动器的弯曲运动模型。首先确定弯曲后曲率半径与顶端位移之间的关系。

图3为驱动器弯曲变形图，θ为弯曲角度，设曲率半径为R。在小变形假设下，通过简单的勾股定理得到曲率半径与驱动器顶端位移之间的几何关系：

直角坐标系下曲率半径还可表示为：

由此可得到内部弯矩方程为：

在准静态下，将内部离子迁移产生的应力场假设为施加在悬臂梁上的均布载荷，对悬臂梁进行分析，如图4所示。当悬臂梁只受均布载荷发生弯曲时，可得出悬臂梁自由端（即x=L处）的挠度为：

其中，EI为整个驱动器的弯曲刚度。

如图5所示，驱动器的宽度为b，PVDF薄膜的厚度为2h1，整个驱動器的厚度为2h2，PPy横截面为平整的平面，则参考图4得到横截面对中心轴的惯性矩：

此时整个驱动器的弯曲刚度即为：

由于施加的电位在有限的范围内 （0～1.0 V） 变化，可认为驱动器的弹性模量是常数，Eppy=80 MPa， EPVDF=440 MPa。

如图6所示，截取梁中长为ds的微段，假设驱动器的弯曲变形为纯弯曲，不受剪力，在发生变形时，绕中性轴转动，相对转角为dθ。横截面上距中性轴为y处的线应变ε可表示为：

驱动器顶端弯矩公式为：

联立公式（2）、（4）、（8）及（9），可得到最大线应变与挠度之间的关系为：

3.2 模型验证

选取3种尺寸的驱动器，测试各种尺寸的驱动器在稳定电压（0 ～1.0 V）下的尖端偏转位移。驱动器尺寸为6 mm×2 mm×0.17 mm、9 mm×2 mm×0.17 mm和12 mm×2 mm×0.17 mm，即3种驱动器只有长度方向尺寸不同，分别为6、9和12 mm。每种尺寸各取3组样品（样品1、2和3），使用激光位移传感器测量驱动器尖端位移，测试结果见表1。由于样品在装夹过程中存在位置误差，且测试环境中不可避免存在振动，3组样品的测试值有差异。取算数平均值为中点，对实验数据进行拟合，结果如图7所示。此线性拟合的拟合度R2分别为0.96641、0.97836和0.96032，说明同一尺寸的驱动器，其顶端位移与施加的电压呈线性关系，电压越大，位移越大。取被测3组数据的算术平均值作为真值，其中样品1的位移值更接近算术平均值，所以选择样品1进行后续实验。

所测得的尖端位移即为挠度（W），由此可建立3种尺寸驱动器的稳定电压与挠度之间的函数关系：

根据驱动器的弯曲运动模型，实验测得驱动器尖端位移x1与y1的值，按公式（2）计算出驱动器顶端的曲率半径值，之后对数据进行拟合。拟合结果如图8所示，3组样品的线性拟合度分别为0.99428＼， 0.99395和0.99278， 说明此线性拟合的结果可靠， 曲率半径与电压之间是非线性关系，随着电压增大，曲率半径值越来越小，说明弯曲程度不断增大。但是，弯曲曲率的增幅逐渐变小，最终趋于稳定，这也说明当电压增加到一定程度时，驱动器的形状会保持不变，不再继续弯曲。由图8得到的数据建立电压与曲率半径之间的函数关系：

为验证以上模型，通过显微镜拍摄的照片对驱动器的曲率半径进行实际测量。3种样品在1.0 V电压下的弯曲变形图如图9所示，样品发生弯曲后形状近似于圆弧，在驱动器的两个端点（夹持端和自由端）分别作圆弧的切线，然后作两条切线的垂线，得到的交点即为圆弧的中心，由此得到圆弧半径R。测量得到的曲率半径数据见表2，并将其与公式（12）计算得到的数据对比，两者之间的偏差较小（<3%），所以，通过测量x、y方向的位移计算曲率半径是合理的。

由公式（7）可求得驱动器刚度值：EI=0.14544 N·mm2，将驱动器的弯曲假想成在悬臂梁上施加一个弯矩值，结合曲率半径计算公式，由公式（3）可求得相应的弯矩值（表3）。由表3可知，驱动器的弯矩值很小，由于本实验制备的弯曲型驱动器尺寸小且柔韧性好，所以得到很小的弯矩值是合理的，验证了模型的有效性。

由公式（4）可得到不同电压下对应的均布载荷的值，建立均布载荷与电压之间的关系式为：

由公式（13）可知，等效均布载荷的方向与电压的正负有关，实际情况下施加的电压正负极不同，驱动器的弯曲情况也不同，所以均布载荷的作用与施加电压使驱动器内部离子迁移导致驱动器弯曲可达到相同的效果。

由公式（10）可知，通过驱动器的弯曲位移可求得驱动器的应变大小，进而得到不同电压下对应的应变值。结果表明，电压与应变接近线性关系，对其进行线性拟合（图10），3组样品的线性拟合度分别为0.98802、0.98353和0.98411，说明此线性拟合的结果较为可靠，而应变随着电压的增加而增大， 也与之前的测试结果相吻合。

对图10中所得数据进行拟合，得出函数关系式为：

拟合得到的公式（14）进一步证实了应变与电压的线性关系，即随着电压增大，应变也随之增大。

4 结 论

依据PPy驱动器的结构及驱动原理，将驱动器等效为悬臂梁结构，建立电-机转换模型。结果表明，测量得到驱动器在低电压下弯曲后的顶端位移，随着电压的增加，顶端位移增大，通过数据的拟合验证了顶端位移与驱动电压呈线性关系; 通过研究驱动器x、y方向的位移，计算得出驱动器的曲率半径，通过实验验证了公式计算曲率半径的合理性; 进而计算出驱动器的弯矩值，验证了模型的合理性，并建立了电压与均布载荷、电压与应变的函数关系式，分别得到两者之间的线性关系。本研究为层状弯曲型PPy驱动器建立了有效的弯曲模型，可用于准确预测此种类型驱动器的变形行为。PPy驱动器可作为微型搅拌器，应用于溶液成分分析测试领域。本研究将为PPy驱动器在溶液成分测试、微纳操纵、生物传感等领域的应用提供可靠的理论模型。

References

1 Gaihre B， Alici G， Spinks G M， Cairney J M. Sens. Actuators A， 2011， 165（2）： 321-328

2 Rasouli H， Naji L， Hosseini M G. Sens. Actuators A， 2018，  279（15）： 204-215

3 Otero T F， Cortes M T. Sens. Actuators A， 2003，  96（1）： 152-156

4 Smela E A. Adv. Mater.，  2003，  15（6）： 481-494

5 Chu S Y， Kilmartin P A， Travas-Sejdic J. Synth. Met.， 2009，  159（21）： 2286-2288

6 Ghazali F A M， Mah C K， AbuZaiter A， Chee P S， Ali M S M. Sens. Actuators A， 2017，  263：  276-284

7 Causley J， Stitzel S， Brady S， Diamond D， Wallace G. Synth. Met.， 2005，  151（1）：  60-64

8 Shahnavaz Z， Lorestani F， Meng W P， Alias Y. J. Solid State Electrochem.， 2015，  19（4）： 1223-1233

9 Lu X， Kong Z， Xiao G， Teng C， Li Y， Ren G， Wang S， Zhu Y， Jiang L. Small， 2017，  13（40）： 1701938

10 ZUO Shuang-Shuang， XI Shuang. Chinese J. Anal. Chem.， 2019，  47（12）：  1960-1966

左雙双， 习 爽. 分析化学， 2019，  47（12）：  1960-1966

11 Du P， Lin X， Zhang X. Sens. Actuators A， 2010，  163（1）： 240-246

12 Hara S， Zama T， Ametani A， Takashimab W， Kaneto K. J. Mater. Chem.， 2004，  14（18）：  2724-2725

13 ZHANG Teng-Teng， WANG Xiang-Jiang， TIAN Su-Kun. Journal of University of South China：  Science and Technology，  2017，  31（4）：  75-79

张腾腾， 王湘江， 田素坤. 南华大学学报： 自然科学版，  2017，  31（4）：  75-79

14 LIU Huai-Min， WANG Xiang-Jiang. Journal of Mechanical & Electrical Engineering， 2015，  （6）： 51-55

刘怀民， 王湘江. 机电工程，  2015，  （6）： 51-55

15 Choudhary R B， Ansari S， Purty B. J. Energy Storage， 2020，  29： 101302

16 Santa A D， Rossi D D， Mazzoldi A. Synth. Met.， 1997，  90（2）： 1-100

17 Metz P， Gürsel A， Spinks G M. Sens. Actuators A， 2006，  130-131： 1-11

18 Nemat-Nasser S. J. Appl. Phys.， 2002，  92（5）： 2899-2915

19 Nguyen C H， Alici G， Wallace G G. Sens. Actuators A， 2012，  185： 82-91