列车荷载下土体时程反应的Ritz向量叠加法

付相球, 潘旦光,2, 柳 艺

(1.北京科技大学 土木与资源工程学院,北京 100083; 2.同济大学 土木工程防灾国家重点实验室,上海 200092; 3.中铁十六局集团有限公司,北京 100018)

0 引 言

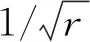
文献[7]对北京地铁八王坟车辆段平台及平台上建筑物进行计算和分析,采用直接积分法计算了建筑物上各点在地铁列车振动荷载下的位移反应时程;文献[8]对比分析了采用振型叠加法和直接积分法计算轨道交通引起的环境振动问题,结果表明直接积分法具有更高的计算效率。这是由于振型叠加法计算时,应使所采用最高振型的频率大于振动输入频率主要范围的最大值,一般认为应达到其2倍[9],而土体固有频率超过100 Hz通常需要几千阶甚至更多的模态,模态分析的计算时间将非常长。但事实上,振型叠加法计算中存在大量的无效模态,因而影响了计算效率。为避免无效模态的影响,文献[10]提出Ritz向量叠加法,该法兼具振型叠加法将耦合方程解耦为单自由度方程的优点,同时考虑到外力荷载的空间分布;文献[11-12]分别应用Ritz向量叠加法分析机械结构及桥梁地震反应,分析结果表明Ritz向量叠加法具有很高的计算效率。

但Ritz向量叠加法的计算精度与Ritz向量个数有关,存在模态截断误差,因此,在进行分析前,需要判断多少阶Ritz向量参与计算。文献[13]分析比较了地震反应中的模态截断方法,但列车荷载与地震荷载形式及卓越频率均存在差异;文献[14]提出基于荷载参与系数的模态截断指标;文献[15-16]给出了基于外荷载空间分布的Ritz向量截断指标。对于轨道交通引起的环境振动这类计算模型很大的问题,关于模态截断指标的选择,以及Ritz向量叠加法的计算效率需进一步研究。为此,本文采用二维分析方法,首先分析了不同Ritz向量截断指标的截断误差与时程反应峰值误差随Ritz向量阶数的变化规律,讨论不同模态截断指标的合理性;然后对比分析了振型叠加法和直接积分法的计算效率,通过不同激振频率下的计算结果验证了研究结论的适用性,所得结果可供类似分析参考。

1 模态截断指标

实际列车荷载引起的振动经钢轨、道床传播至周围土体,为了简化分析,以土体为分析对象,把经由铁轨和路基传至下方土体表面的荷载作为列车荷载,即列车-轨道-道床系统整体作为外力激励,列车荷载作用下的土体动力反应可简化为二维土体单点激励的分析模型[17],此时,N个自由度的土体结构运动方程为:

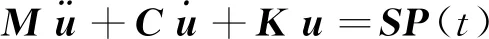
(1)

(2)

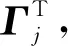
(3)

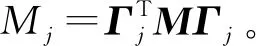
通常,Ritz向量叠加法采用少数低阶Ritz向量进行计算,即可得到满足计算精度要求的结果,因此计算效率高,但由此存在截断误差。为使截断误差控制在合理的范围内,需要截取足够的Ritz向量个数n。因此,在应用Ritz向量叠加法计算时,需要提前判断n的取值,目前常用的截断方法[14-16]可以归纳为基于动力贡献和基于外力分布2种。

1.1 基于动力贡献截断方法

基于动力贡献Ritz向量截断方法假定(1)式、(3)式左边只有动力项,只有惯性力抵抗外部荷载,即

(4)

(5)

其中,M为对角矩阵。由(4)式可以得到单位荷载作用下拟加速度的精确解,由(5)式可以得到单位荷载作用下拟加速度的近似解,由此得到基于动力贡献的Ritz向量截断误差指标[14]可以表示为:

(6)

1.2 基于外力分布截断方法

根据递推迭代得到的Ritz向量矩阵Γ,外力荷载的空间分布向量S′可以表示为:

(7)

其中,aj为展开式系数;M1/2为M对角元素的平方根矩阵。当n=N时S′即为S;仅保留n个Ritz向量时,相当于计算结构动力响应时只考虑了荷载的部分影响。

文献[15]中定义的激振力截断误差指标为:

(8)

文献[16]中提出的基于外荷载空间分布的截断误差指标定义为:

(9)

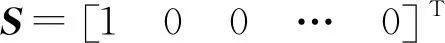
2 模态截断方法的影响

2.1 算例模型

二维均匀土体计算模型如图1所示,根据文献[4]结果,土体研究区域取宽50 m、深20 m的范围,横向边界只约束宽度方向,底面边界刚性约束,土体为对称模型,取1/2土体进行分析。

图1 二维均匀土体模型

线弹性范围内,列车荷载可采用Fourier变换分解为一系列简谐函数的和[18],因此,本文将列车荷载简化为简谐函数,即

P(t)=SAsin(2πft)

(10)

其中,A为列车峰值荷载;f为激振频率。

土体采用二维平面单元离散,有限元模型单元划分如图2所示。

图2 有限元模型单元划分

单元的长度控制要求为:

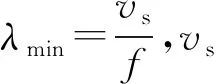
土体密度取2 000 kg/m3,弹性模量取200 GPa,泊松比取0.35,则土体的剪切波速vs≈200 m/s。当f取为主要的激振频率50 Hz时,λmin=4 m,则l≤(0.5～1.0) m即可满足要求。因此,图2中有限元模型的单元长度均不超过1.0 m,靠近激励点单元划分加密,模型共包含2 376个节点,4 550个自由度。

因为列车运行产生的环境振动中,表面波占主要地位,所以计算模型主要分析土体表面1#到6#点的位移反应,其中1#～6#点距离荷载施加点水平距离依次为0、2、4、6、8、10 m,1#～6#点的竖向位移分别定义为体系的第1个到第6个自由度。

2.2 Ritz向量叠加法计算结果及截断误差分析

基于简化的二维土体模型,考虑所有N个Ritz向量叠加,得到2个荷载周期内1#～6#点位移时程反应的精确解,如图3所示。从图3可以看出,列车荷载在土体表面衰减很快,距离激励位置1#点水平距离为10 m的6#点峰值位移衰减到1#点的5%左右,进一步验证了土域范围取值合理。

图3 1#～6#点位移时程反应曲线

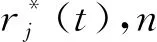
(11)

则1#～6#点竖向位移时程反应峰值误差分别记为e1、e2、e3、e4、e5、e6。

各自由度误差和截断指标小于5%时,n的取值见表1所列。

表1 误差控制在5%以内时n的取值

不同自由度的位移反应峰值误差e1～e6以及基于动力贡献的截断误差D和外力分布的截断误差λ随Ritz向量个数n的变化如图4所示。

图4 Ritz向量截断误差

从图4和表1可以看出:① 1#～6#点峰值位移反应误差ei在前几个Ritz向量下存在起伏,整体趋势随着n增加而减小,超过65个Ritz向量后峰值位移反应误差均低于5%且很快收敛至接近于0;② Ritz向量截断误差低于5%时,选取的模态阶数依据D为126阶,依据λ为2 600阶,其截断误差均大于峰值位移反应误差,但基于λ选取的n比实际所需的多出太多,增加了大量多余的计算量,而基于D截取的n略大于实际所需的向量数目,适合作为列车荷载下Ritz向量叠加法进行模态截断的依据。

3 不同算法计算效率对比

为了对比不同方法的计算效率,对图2的计算模型,分别应用Ritz向量叠加法、振型叠加法和直接积分法进行计算。

对于振型叠加法,考虑常阻尼比,通过计算得到不同模态截断阶数n下1#～6#点竖向峰值位移误差ej,如图5所示。

图5 振型叠加法截断误差

从图5可以看出,当计算超过4 000阶模态时,e1～e6都在5%以内,因此,振型叠加法可以取4 000阶模态进行时程反应分析。

对于直接积分法,考虑经典瑞利阻尼矩阵,根据文献[8]直接积分法计算轨道交通振动的结论,可以取第1阶固有频率和荷载频率计算瑞利阻尼系数。

Ritz向量叠加法按D<5%时计算,即计算126个Ritz向量。精确解为采用Ritz向量叠加法计算全部N个Ritz向量的分析结果。

1#点3种方法计算结果与精确解在1个荷载周期内位移时程反应如图6所示,1#～6#点峰值位移结果如图7所示。

从图6、图7可以看出,3种方法计算结果接近,均可满足计算精度要求。

图6 1#点位移时程反应

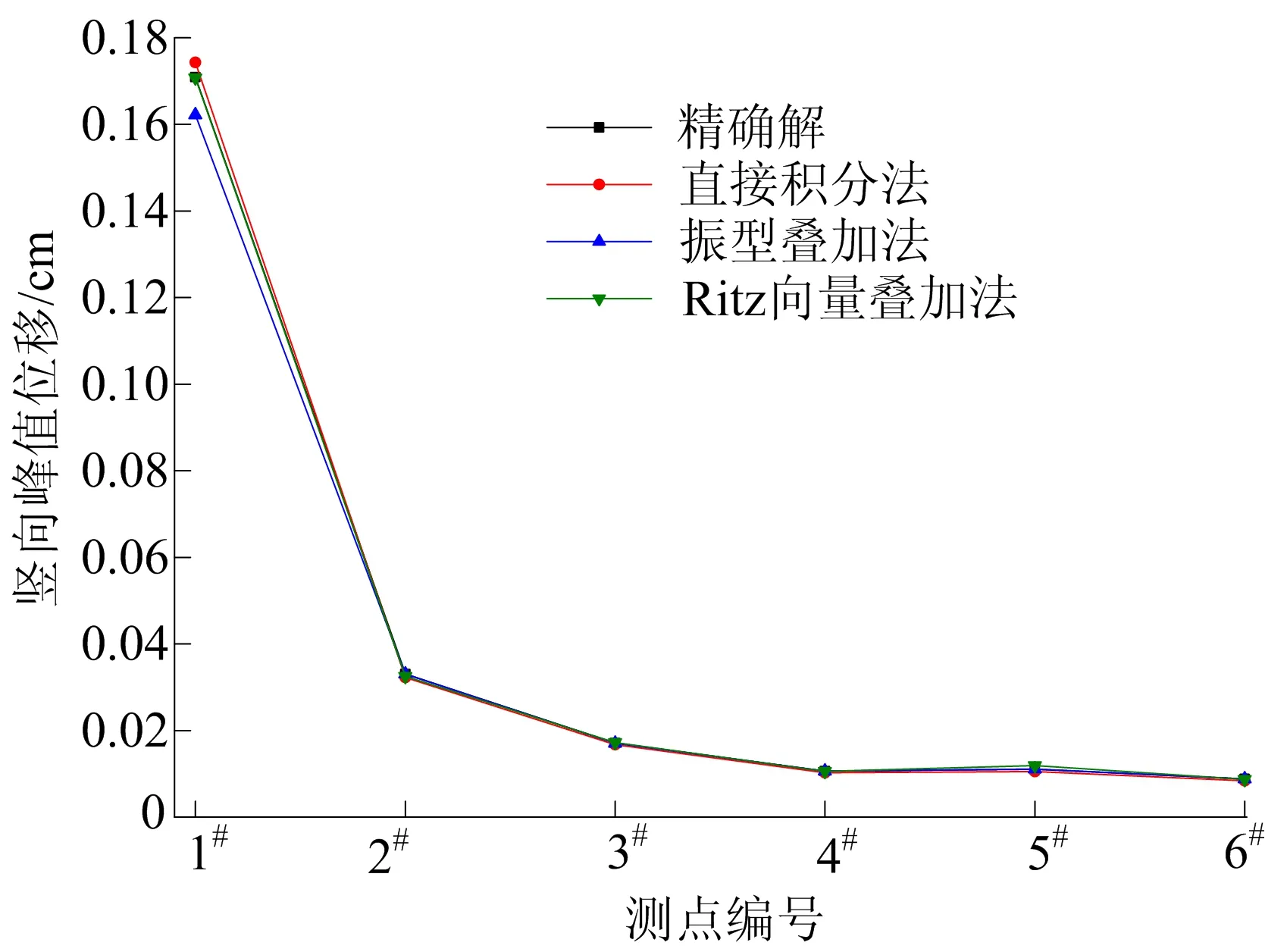
图7 1#～6#点峰值位移

3种方法在相同软硬件环境下的计算时间见表2所列。

从表2可以看出，对于本文算例模型,Ritz向量叠加法仅需12 s,计算时间远小于其他2种方法,其计算效率明显高于其他2种方法;振型叠加法计算效率最低,直接积分法计算效率居中。

表2 3种方法计算耗时对比

4 不同激振频率计算结果

地铁荷载频率成分复杂,真实地铁荷载是不同频率成分的叠加,主要频率范围在30～80 Hz之间,为了验证上述研究结论在列车荷载主要频率范围内的适用性,对比分析(10)式中f为10、30、50、70、90 Hz下的计算结果。其中,D和λ与荷载频率无关,f不同取值下结果和50 Hz情况相同。ej控制在5%以内时，n的取值见表3所列。

从表3可以看出,随着f增大,n增加,但均略小于基于D截取的126个Ritz向量个数,基于λ选取的Ritz向量个数仍比实际所需的多出太多,因此在列车荷载频率范围内,D适合作为模态截断的依据。

表3 ej控制在5%以内时n的取值

Ritz向量叠加法与直接积分法的计算效率和f无关,不同f下计算耗时也与50 Hz一致,振型叠加法的计算耗时随f的变化结果见表4所列。

从表2、表4可以看出,地铁荷载频率范围内,不同f对振型叠加法计算效率影响不大,Ritz向量叠加法计算效率仍然明显高于其他2种方法。

表4 不同f下振型叠加法计算耗时

5 结 论

本文研究Ritz向量叠加法在轨道交通引起土体振动中的应用及相应的Ritz向量截断问题,首先分析模态截断指标和土层峰值位移反应误差随向量阶数的变化规律,讨论不同模态截断指标的合理性,然后对比分析了Ritz向量叠加法、振型叠加法及直接积分法3种方法的计算效率,最后通过不同激振频率下的计算结果验证了研究结论的适用性。

(1) 基于动力贡献的截断指标与Ritz向量截断误差的变化规律相同,且由截断指标所得向量数目略大于实际所需的向量,适合作为Ritz向量截断的依据。

(2) 在计算精度基本相同的情况下,振型叠加法的计算耗时最长、直接积分法次之,Ritz向量叠加法最短。