环Fpk+uFpk上的(1-u)-循环码
2020-12-05张秋红朱士信
张秋红, 朱士信
(合肥工业大学 数学学院,安徽 合肥 230601)
0 引 言
一直以来,环上的线性码和循环码被人们加以定义和广泛研究。文献[1]证明了通过Gray映射能够由环Z4上的线性码得到好的非线性二元码,该环上的负循环码在文献[2]中有详细的描述。文献[3]则通过布尔函数讨论了环Z2k上码的性质,而在文献[4]中进一步研究了环Zpk+1上(1-pk)-循环码,得到了环Zpk+1上循环码的结构及其Gray像的关系,文献[5]用另一种证明方法给出了环Zpm上循环码的结构。近几年,多项式剩余类环上的线性码也引起了人们的兴趣。关于多项式剩余类环上循环码的性质在文献[6-9]中有较详细的介绍。
环上循环码的结构是编码理论很重要的组成部分,因此,研究环上循环码的结构是很有意义的。本文定义了剩余类环R=Fpk+uFpk上(1-u)-循环码,通过一个从R[x]/〈xn-1〉到R[x]/〈xn-(1-u)〉的同构映射,讨论了(1-u)-循环码的结构,给出了其生成多项式及其码字的个数。特别地,在p=2时,给出了其对偶码的生成多项式和自对偶码存在的一个充要条件。需要特别指出的是,本文出现的p为素数,且(n,p)=1。
1 预备知识
通常情况下,多项式剩余类环指Fp[u]/〈w(u)k+1〉,其中k>1,p是任意素数,而w(u)是Fp上次数为m≥1的不可约多项式。有限链环Fpk+uFpk是指Fpk[u]/〈u2〉。本文考虑的即为有限环Fpk+uFpk,记R=Fpk+uFpk,其极大理想为uR,剩余域为Fpk。

对∀x=(x1,x2,…,xn),y=(y1,y2,…,yn),定义点积x·y=x1y1+x2y2+…+xnyn。
定义1 设v是Rn→Rn的映射,v(a0,a1,…,an-1)=((1-u)an-1,a0,a1,…,an-2),则称v是Rn上(1-u)-循环变换。
定义2 设v是Rn上(1-u)-循环变换,若Rn的加法子群C满足∀c∈C,v(c)=c,则称C是环R上(1-u)-循环码。
定义3 令C⊥={u∈Rn,u·v=0,对∀v∈C},则称C⊥为C的对偶码。
定义4设f(x)、g(x)∈R[x],若f(x)·g(x)=xn-(1-u),则称g(x)为f(x)的零化多项式。
2 环R上(1-u)-循环码
引理1[4]环R上长为n的线性码C是(1-u)-循环码当且仅当P(C)是R[x]/〈xn-(1-u)〉的理想。
当(n,p)=1时,存在n1∈{0,1,…,p-1},使得n·n1=1(modp),令β=1+n1u∈R,则对任意i∈Z,有βi=1+in1u∈R,特别地,βn=1+u∈R,且β-n=1-u∈R。由此,作映射u满足:
u:R[x]/〈xn-1〉→R[x]/
〈xn-(1-u)〉r(x)→r(βx),
显然,u是一个同构映射,且I是R[x]/〈xn-1〉的理想当且仅当u(I)是R[x]/〈xn-(1-u)〉的理想。
为了方便,记Rn=R[x]/〈xn-1〉,则环Rn是主理想环[1]。
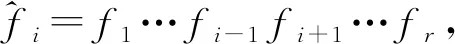
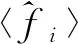
定理1 (1) 环R[x]/〈xn-(1-u)〉为主理想环。
(2) 设C是R上长为n的(1-u)-循环码,则xn-1在环Fpk上的素分解为:
xn-1=A(x)B(x)C(x)。
令P(C)=〈A1(x)B1(x),uA1(x)C1(x)〉,
其中
A1(x)=β-deg A(x)A(βx);
B1(x)=β-deg B(x)B(βx);
C1(x)=β-deg C(x)C(βx);
β=1+n1u。
则P(C)由A1(x)(B1(x)+u)生成。
(3)C的基数为p2kdeg C1(x)+kdeg B1(x)。
为了方便,本文将多项式A(x)简记为A。
证明(1)Rn=R[x]/〈xn-1〉是主理想环,映射u为同构映射,因此环R[x]/〈xn-(1-u)〉为主理想环。
(2) 由A、B、C两两互素可得A1、B1、C1两两互素,由P(C)=〈A1B1,uA1C1〉得到A1B1、uA1B1、uA1B1∈P(C),又B1、C1互素,uA1∈P(C),因此,G=A1(B1+u)∈P(C),故〈G〉⊆P(C);反之,在环R[x]/〈xn-(1-u)〉中,A1(x)·B1(x)·C1(x)=xn-(1-u),uA1C1=(G-A1·B1)C1=GC1(mod(xn-1)),故uA1C1∈〈G〉,又uG=uA1·B1∈〈G〉,uA1∈〈G〉,则A1·B1=G-uA1∈〈G〉,P(C)⊆〈G〉,因此P(C)=〈G〉=〈A1(B1+u)〉。
(3) 由P(C)=〈A1(B1+u)〉,可得:
|P(C)|=p2k(n-deg A1-deg B1)pk(n-deg A1-deg C1)=
p2kdeg C1(x)+kdeg B1(x)。
3 F2k+uF2k上(1-u)-循环码的对偶码
引理3 设C是环R上长为n的(1-u)-循环码,则C⊥是(1+u)-循环码。
证明设(a0,a1,…,an)∈C⊥,对∀(c0,c1,…,cn-1)∈C,则有:
((1-u)c1,(1-u)c2,…,(1-u)cn-1,c0)∈C,
(a0,…,an-1)·((1-u)c1,(1-u)c2,…,(1-u)cn-1,c0)=(1-u)c1a0+(1-u)c2a1+…+(1-u)cn-1an-2+c0an-1=0。
如果两边同时乘以1+u,可得:
c1a0+c2a1+…+cn-1an-2+(1+u)c0an-1=0,
那么((1+u)an-1,a0,a1,…,an-2)∈C⊥,因此C⊥为(1+u)-循环码。
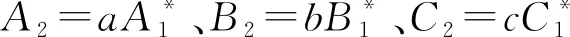
(1)C⊥是(1-u)-循环码,且P(C⊥)=〈C2B2,uC2A2〉,P(C⊥)由C2(B2+u)生成。
(2)C⊥的基数为22kdeg A2+kdeg B2。
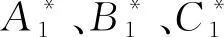
证明(1)可分别由引理2和定理1直接得出。
(2)由引理3,C⊥为F2k+uF2k上(1+u)-循环码,又〈A1〉⊥=〈B2C2〉,且P(C)=〈A1B1,uA1C1〉⊆〈A1〉,因此,〈A1〉⊥⊆C⊥,即〈C2B2〉⊆C⊥。类似地,〈uC2A2〉⊆〈C2〉=〈A1B1〉⊥,〈uC2A2〉⊆〈uA1C1〉⊥,则〈uC2A2〉⊆〈A1B1〉⊥∩〈uA1C1〉⊥=C⊥,故〈C2B2,uC2A2〉⊆C⊥。又|〈C2B2,uC2A2〉|=22kdeg A2+kdeg B2,|C|=22kdeg C1+kdeg B1,|C||C⊥|=|R|n,|C⊥|=22kdeg A1+kdeg B1,degA2=degA1degB2=degB1,由此可得|〈C2B2,uC2A2〉|=|C⊥|,因此P(C⊥)=〈C2B2,uC2A2〉。
类似定理1的证明,可得P(C⊥)是由C2(B2+u)生成的。
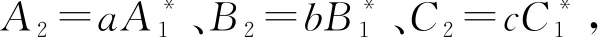
证明当C为自对偶码时,P(C)=P(C⊥),C⊥的生成多项式P(C)是C的生成多项式的零化多项式的互反多项式,且P(C)·P(C⊥)=0。
例1 在环F4+uF4上,设C是该环上长为7的(1-u)-循环码,x7-(1+u)=(x-(1+u))(x3+(1+u)x2+1+u)(x3+x+1+u)。
令A1=(x3+(1+u)x2+1+u),B1=(x-(1+u)),C1=(x3+x+1+u),P(C)=〈A1B1,uA1C1〉,则由定理3知,C为自对偶码,且P(C⊥)=〈C2B2,uC2A2〉,|C|=|C⊥|=4622。
4 结 论
本文给出了环Fpk+uFpk上(1-u)-循环码的生成多项式和码的基数,以及环F2k+uF2k上(1+u)-循环码的对偶码的多项式及其自对偶的条件,关于剩余类环Fpk+uFpk+…+uk-1Fpk上线性码的更多研究必将极大地丰富有限环上的编码理论的发展。
