基于预测有效度的ICOWA算子区间组合预测模型
2020-12-05郝江锋陈华友朱家明
魏 欣, 郝江锋, 陈华友, 朱家明
(1.安徽大学 数学科学学院,安徽 合肥 230601; 2.巢湖学院 数学与统计学院,安徽 合肥 238000; 3.安徽大学 互联网学院,安徽 合肥 230039)
0 引 言
由于传统的单项预测方法所利用的信息较少,一旦单项预测方法选择错误,就会给预测带来较大误差。因此文献[1]在1969年首次提出了组合预测方法。所谓组合预测就是将不同的单项预测模型的预测结果,利用加权算术平均、加权几何平均或加权调和平均等加权平均形式进行组合,在一定的优化准则下构建相应的数学模型,其目的是综合利用各种单项预测模型所提供的有效信息。组合预测方法逐渐得到学者们的关注,而前期对组合预测的研究大多是对单点值的研究,然而在现实世界中,会出现很多不确定的信息,此时若只考虑一个数值,则会引起较大的误差。文献[2]给出了区间数的运算法则;文献[3]通过区间数的形式描述了组合预测模型,建立了相应的区间型组合预测模型,结果表明,该模型具有更好的预测效果。
一些传统的组合预测方法往往对不同的单项预测方法赋予固定的权系数,这种赋权方法是默认不同的单项预测方法在各个时刻的表现大体相同,实际上不同的单项预测方法在不同时刻的预测精度并不相同,因此传统的固定权系数的组合预测模型存在赋权缺陷。
文献[4]提出了诱导有序加权平均(induced ordered weighted averaging,IOWA)算子的概念;在此基础上,文献[5]对区间数的组合预测进行了初步的研究,建立了基于IOWA算子的区间预测模型,该模型考虑了不同时点的预测精度,将预测精度作为诱导变量对各种单项预测方法进行有序加权平均,提高了预测精度;文献[6]则将诱导有序加权平均(IOWA)算子和连续有序加权平均(continuous ordered weighted averaging,COWA)算子结合,提出了诱导连续有序加权平均(induced continuous ordered weighted averaging,ICOWA)算子,并进行了相应的实例分析,提高了预测的精度。
现有的组合预测方法有关权系数的计算中,实际应用较多的是最小方差法,并且大部分是用绝对误差作为准则来计算组合预测方法的权系数,这些方法大多是为了改善某种拟合的误差而建立起来的。文献[7]详细分析了组合预测模型权重的计算方法,实际上预测有效度也是反映预测精度的有效指标之一;文献[8]提出基于预测有效度的组合预测模型。预测有效度分为一阶预测有效度和二阶预测有效度。一阶预测有效度主要考虑预测模型的精度,但一个好的预测方法,不但要求在预测精度上有良好的表现,而且要求在预测精度的稳定性上表现良好,为此提出二阶预测有效度的概念[7]。
本文是在不确定信息的背景下,将二阶预测有效度指标和ICOWA算子相结合,以各模型的预测精度作为诱导值进行集结,建立了基于二阶预测有效度的ICOWA算子的区间组合预测模型。该模型将二阶预测有效度的极大化作为目标函数,最后通过实例验证了该模型的可行性。
1 预备知识
定义1[9]设a=[aL,aU]={x|aL≤x≤aU},其中aL,aU为实数,则称a为一个区间数。
记m=(aL+aU)/2,r=(aU-aL)/2,则称m为区间的中心r为区间的半径,区间数可记为a=[aL,aU]=(m;r)。
若有2个区间数:
a=[aL,aU]=(m1;r1),
b=[bL,bU]=(m2;r2),λ∈R,
则它们之间的运算法则如下。
加法运算:
a+b=[aL+bL,aU+bU]=
(m1+m2;r1+r2);
减法运算:
a-b=[aL-bU,aU-bL]=
(m1-m2;r1-r2);
数乘运算:
定义2[10]设[a,b]为区间数,令

(1)
则称FQ为连续有序加权平均(COWA)算子。其中函数Q: [0, 1]→[0, 1]为基本单位区间单调(basic unit monotonous,BUM)函数,满足Q(0)=0、Q(1)=1;且若x>y,则Q(x)≥Q(y)。

FQ([a,b])=λb+(1-λ)a。
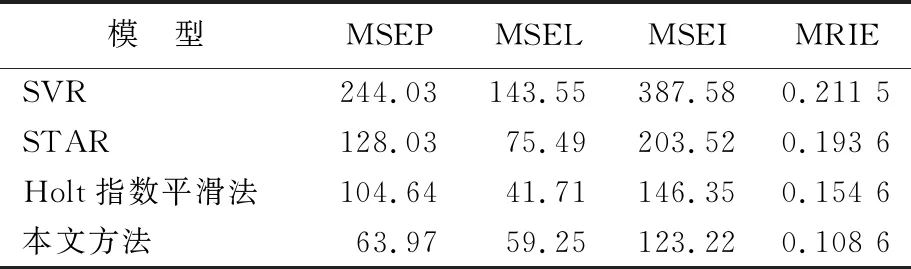
定义3[9]设f:Ω+→R+,其中,Ω+={[a,b]|,a∈R+,b∈R+,a f(〈u1,[a1,b1]〉,〈u2,[a2,b2]〉,…, (2) 则称[ai,bi](i=1,2,…,n)为诱导连续区间有序加权平均(ICOWA)算子。其中,l=(l1,l2,…,ln)是与[ai,bi](i=1,2,…,n)有关的加权向量,满足非负性和归一化;[ai,bi](i=1,2,…,n)称为诱导变量;u-index(i)是u1,u2,…,un中第i大数所对应的下标。 ICOWA算子的基本特征是利用COWA算子对区间数据[ai,bi](i=1,2,…,n)进行集成之后,再对集成的结果利用IOWA算子进行诱导有序加权平均。 设某社会经济现象的时间序列指标观察值为{xt|t=1,2,…,N},其中xt=[at,bt]=(mt;rt),有m种单项预测方法对其进行预测。xit=[ait,bit]=(mit;rit)为第i种预测方法在第t时刻上的区间预测值,i=1,2,…,m;t=1,2,…,N。eit为第i种预测方法在第t时刻的预测相对误差,Ait=1-|eit|为第i种预测方法在第t时刻的预测精度。 定义4[11]称Mi=E(Ai)(1-σ(Ai))为第i种预测方法的二阶预测有效度,i=1,2,…,m,其中 (3) 定义5[12]令 (4) 则称uit为第i种单项预测方法在第t时刻的预测精度,i=1,2,…,m;t=1,2,…,N。 显然uit∈[0,1],可以把uit当作预测值[ait,bit]的诱导值,即根据每一个uit与之相应的预测值[ait,bit],构成m个二维数组〈u1t,[a1t,b1t]〉, 〈u2t,[a2t,b2t]〉, …,〈umt,[amt,bmt]〉。 由定义2可以得到,由实际区间值及COWA算子生成的t时刻的实际集结值FQ(xt)=FQ([at,bt])和各单项预测方法在t时刻预测值的集结值FQ(xit)=FQ([ait,bit]);再由定义3,可以得到ICOWA算子生成的t时刻的组合预测值,计算公式为: (5) 定义6[13]令 i=1,2,…,m;t=1,2,…,N (6) 则称eit为第i种单项预测方法在第t时刻基于连续有序加权平均(COWM)算子的区间预测的相对误差。 i=1,2,…,m;t=1,2,…,N (7) 则称eu-index(it)为由区间预测精度序列u1t,u2t,…,umt作为诱导变量所产生的第i大的基于ICOWA算子的预测相对误差。 由(5)~(7)式可得组合预测的相对误差为: (8) 设At为第t时刻的组合预测精度,则有: At=1-|et|= 根据定义4,基于ICOWA算子的组合预测的二阶预测有效度M为: M=E(A)(1-σ(A))= 其中,E(A)为组合预测方法的预测精度序列的数学期望;σ(A)为预测精度序列的标准差。显然,E(A)和σ(A)是各种单项预测方法加权系数l1,l2,…,lm的函数,因此M也是l1,l2,…,lm的函数,记为M(l1,l2,…,lm)。 一般地,M(l1,l2,…,lm)越大表示组合预测方法越有效,因此基于二阶预测有效度的ICOWA算子的区间组合预测模型可表示为: (9) 文献[14]针对实数型预测有效度的组合预测模型探讨了其近似求解算法。本文建立的模型(9) 式也是关于权系数的非线性规划问题,且目标函数是非光滑的。在文献[14]的基础上,可以得到基于二阶预测有效度的ICOWA算子的区间组合预测模型预测精度序列的一个性质。 定理1 模型(9)式组合预测方法的预测精度序列{At|t=1,2,…,N}的数学期望E(A)和标准差σ(A)满足: (10) 其中,Aa-index(it)=1-|ea-index(it)|为ICOWA算子在第t时刻的预测精度。 证明设ea-index(it)为ICOWA算子的预测相对误差,i=1,2,…,m;t=1,2,…,N,则有: 因此 (11) (12) 考虑到双重求和符号的可交换性,则有: (13) 从而由(12)式、(13)式得: 注意到(11)式,存在α0∈[0,1],使得: 因此有: (14) 将(14)式代入到标准差σ(A),则有: (15) 其中 [Aa-index(jt)-E(Aa-index(jt))]} (16) 即pij为ICOWA算子预测精度序列的相关系数。因为pij∈[-1,1],所以有: (17) 综上,定理1证毕。 按照定理1,组合预测模型可以表示为如下新的非线性规划模型: (18) 其中,α0∈[0,1]为常数。模型(18)式比模型(9)式更加简洁,易于求解。 为了说明本文提出的基于二阶预测有效度的ICOWA算子的组合预测模型的有效性,引用文献[9]中的数据进行实例分析,实例分析数据见表1所列。 表1 实际区间值和单项预测方法的预测区间值 以下就实例分析计算步骤进行简要说明。 根据(4)式,计算出各单项预测方法在各个时刻点处的预测精度值序列,见表2所列。 表2 单项预测方法的预测精度值序列 根据各单项预测方法在某一时刻的预测精度,将预测精度按照从小到大排序,进而可以得到预测精度所对应的预测区间[au-index(it),bu-index(it)]的数据,见表3所列。 根据(5)式,计算出各单项预测方法的预测相对误差和预测精度序列,见表4所列,再根据所得到的预测区间的排序值,计算出预测相对误差和预测精度序列的排序值,见表5所列。 表3 由预测精度排序所得到的预测区间值的排序 表4 各单项预测方法的相对误差和预测精度序列 表5 由预测精度排序得到的相对误差和预测精度序列 由(3)式和(16)式计算可得: p12=p21=0.411 2;p13=p31=-0.265 5; p23=p32=-0.256 6。 将上述值代入模型(18)式可得最优模型如下: 2l1l2×1.28 86×10-3+2l1l3× (-5.043×10-4)+ 其中,l1+l2+l3=1;l1≥0,l2≥0,l3≥0。 取α0=0.1,利用lingo优化软件计算得到组合预测的权系数为: l1=1,l2=0,l3=0,M=0.995 0。 由此可以发现,l2=0,l3=0并不代表它是冗余预测模型,而是表明未来的组合预测是把这3种单项预测方法的预测值中精度高的作为其新的预测值。 为了更好地评定模型效果,根据预测的评价原则,分别计算模型1、模型2、模型3以及本文预测方法的各预测精度指标[15]。 平均区间位置误差平方和: 平均区间长度误差平方和: 平均区间误差平方和: MSEI=MSEP+MSEL= 平均区间相对误差和: 计算结果见表6所列。 表6 各模型精度比较 从表6可以看出,本文所提出的组合预测方法预测误差指标值除了MSEL均低于另外3种单项预测方法,说明本文提出的方法的预测效果更好。 为了进一步说明本文提出的组合预测模型的有效性,引用合肥市2018年12月空气质量指数作为原始数据,运用支持向量回归(support vectaregression,SVR)、平滑转移自回归(smoothtransition autoregression,STAR)、Holt指数平滑法作为单项预测方法对原始数据进行预测,结果见表7所列。 按照上例所示方法进行同样计算,可得组合预测结果,将各单项预测方法和组合预测方法的误差进行比较分析,见表8所列。 表7 实际区间值和单项预测方法的预测区间值 表8 各模型精度比较 从表8可以看出,本文所提出的组合预测方法预测误差指标值除了MSEL均明显低于另外3种单项预测方法,进一步说明本文提出方法的预测效果更好。 本文将二阶预测有效度和ICOWA算子相结合,构建了一个新的变权组合预测模型;将二阶预测有效度引入到区间组合预测,并用实例进行了分析,验证了本文提出的组合预测模型的有效性。实验结果表明,本文方法能够综合利用各单项预测方法所提供的有效信息,是优性组合预测模型。2 区间模型的构建


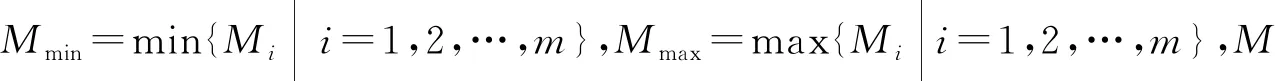
3 区间组合预测模型的近似求解
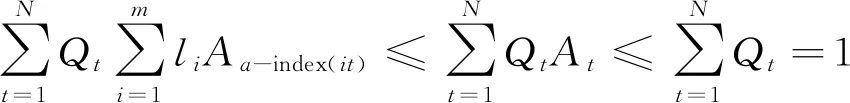


4 实例分析


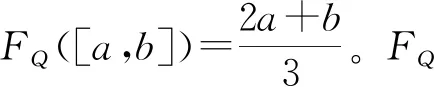





5 结 论
