减小大跨上承式铁路拱桥梁端转角的有效方法

谢肖礼, 庞木林, 邱 辰, 覃石生

(广西大学 土木建筑工程学院,广西 南宁 530004)

上承式拱桥刚度较大,在跨越山区河流、深谷时有巨大优势,因而成为我国西南地区高速铁路线上的常用桥型[1-5],如目前在建的大瑞铁路怒江四线特大桥[6](位于云南,主跨达490 m)、沪昆高铁北盘江特大桥[7](位于贵州,主跨为445 m)等。

高速铁路对轨道的平顺性和稳定性有着严格要求,文献[8]对梁端转角的大小亦有严格限制[9-10]。无砟轨道自重比有砟轨道轻,且具有良好的稳定性、平顺性和耐久性,在高速铁路上的应用越来越广泛[11]。但是随着跨径及荷载的不断增加,拱桥的L/4跨处在列车静活载作用下所产生的上挠度会愈来愈大,对列车安全行进不利。列车提速后,高铁桥梁所承受的作用力亦不断增大,而无砟轨道的轨道系统与桥梁处于较大的刚性连接状态,梁端的微小转角都将对轨道系统产生很大影响[12-13]:一方面,梁端转角的存在增大了列车对轨道的冲击作用,这对轨道结构的稳定性和耐久性非常不利[14];另一方面,过大的梁端转角会使列车响应增大,从而降低行车安全性和舒适性。

国内研究者对无砟轨道的梁端转角开展了大量研究。文献[12]对大跨度钢桥梁端无砟轨道结构受力进行了计算分析;文献[15-16]讨论了大跨公铁两用悬索桥梁端转角对列车走行性的影响,还研究了大跨度铁路桥梁梁端伸缩装置对列车走行性的影响;文献[17]分析了高墩大跨桥梁变形对无砟轨道的影响;文献[18]研究了桥梁竖向变形对轨道平顺性的影响;文献[19]探讨了梁端转角对轨道结构受力的影响规律;文献[20]对铜陵公铁两用长江大桥梁端竖向转角控制进行设计研究。

此外,关于梁端转角对扣件系统影响的研究也是热点之一。文献[14]研究了梁端位移对无砟轨道扣件系统的影响;文献[21]对客运专线无砟轨道梁端扣件上拔力进行了研究;文献[22]探讨了梁端转角对梁端扣件的影响;文献[23]对梁端无砟轨道扣件系统受力进行了研究。

然而,上述研究成果仅揭示了梁端转角产生的机理与危害,涉及减小梁端转角的相关研究很少。因此,有必要在上述研究成果的基础上,寻求有效方法减小梁端转角,以保持桥上轨道的平顺性,保证列车安全快速通行。

梁端转角的产生分2个方面:① 总体加载时梁端产生的总体转角;② 列车轮对作用时桥面局部变形产生的局部转角。桥梁是轨道的承托者,其自身刚度必须足够大才能保证轨道具备高平顺性和高稳定性[10]。桥梁存在梁端转角时,钢轨在无砟轨道层间作用下将出现“上凸”和“下凹”现象,并且这种现象随转角值的增大而越发明显。为使列车维持高速、舒适、安全运行,桥梁在巨大动力作用下不能出现较大挠度和振幅,因此,设法提高桥梁刚度是减小梁端转角最直接、最根本的途径。

基于此,本文提出一种有效方法,即在桥面系与拱肋间增设V形腹杆以形成带多点弹性约束的变高桁架,通过适时的体系转换使拱和桁架分阶段承担荷载,利用桁架结构承担活载的优势,提高拱桥的整体刚度,进而减小梁端转角。为方便叙述,将新结构统称为“本文拱桥”。本文介绍了其结构形式和力学原理,并对跨径为10 m的实验桥进行静载实验,同时利用有限元软件进行计算,以验证方法的有效性。

1 本文拱桥结构形式与力学原理

1.1 结构形式

本文拱桥的结构形式如图1所示。

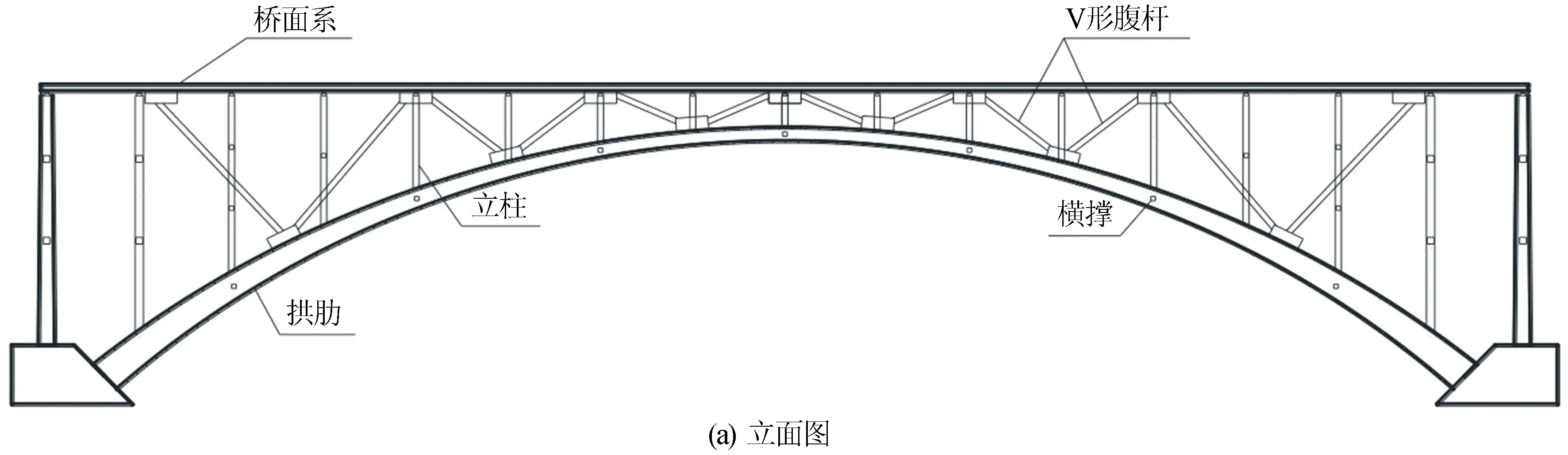
图1 本文拱桥结构布置

在设计荷载确定的条件下,梁端转角与桥梁自身刚度有关,因此,减小梁端转角的关键在于提高结构的刚度,本文力求在增加用钢量很少的条件下通过大幅提高结构的刚度,最终实现减小梁端转角的目标。

本文利用传统上承式拱桥桥面系与拱肋存在一定空间距离的特点,通过在两者间增设V形腹杆,使其与桥面系及拱肋一起形成一个带多点弹性约束的桁架结构,发挥桁式结构承担活载的优越性,通过提高拱桥刚度进而减小梁端转角。

1.2 力学原理

1.2.1 体系转换

铁路桥梁活载大、冲击力强,一般地说,利用刚度大的桁式结构承担活载有更大的优越性。桁式结构的基本结构为三角形,本文拱桥将现有的桥面系及拱肋分别视为上弦杆和下弦杆,V形腹杆加入后,可形成多个连续的三角形结构,利用三角形稳定性有效约束桥面系及拱肋,可增加两者的线刚度,最终使结构刚度大幅提高。三角形只在受节点力作用的情况下才具备良好的稳定性,由于活载处于移动状态,其在桥梁上的作用点不唯一,因而以上形成的三角形将受非节点力作用,稳定性会降低,但是立柱对桥面系提供的弹性约束可提高其线刚度并减小剪切及弯曲变形,故三角形的稳定性仍可得到保证。

目前,关于上承式拱桥的设计理念和规范中,恒载和活载均由拱肋承担,但是,2种荷载使拱肋产生的响应却各有不同。在恒载作用下拱肋为小偏心受压构件,而活载作用下拱肋同时存在压、弯、剪变形,可见,只用一种构件承担所有荷载,其设计方法存在一定的不合理性。为使恒载和活载能由不同结构承担,本文拱桥在依照传统上承式拱桥体系成桥后,再安装V形腹杆完成体系转换,如图2所示,然后上二期恒载,最终成桥。

图2 本文拱桥体系转换示意图

从设计理念上看,拱和桁架分阶段参与承担荷载,可充分发挥拱和桁架的优越性。从受力上看,本文拱桥的一期恒载由拱肋承担,可充分发挥拱结构的优越性;二期恒载及活载则由一个带多点弹性约束的变高桁架结构来承担,以桁式结构承担活载,可增大结构的整体刚度,进而有效减小梁端转角。

1.2.2 V形腹杆位置与数量的确定

V形腹杆设置的位置对提高结构刚度的有效性具有重要影响,而腹杆的数量直接影响着经济性及结构对温度变化的敏感程度,因此必须科学确定V形腹杆的位置及数量。上承式拱桥在恒载作用下的挠度曲线如图3所示,在活载作用下的下挠位移包络图如图4所示。由图3、图4可知,结构在恒载作用下的最大变形位置发生在跨中,活载作用下的最大位移发生在L/4和3L/4附近。

图3 恒载作用下上承式拱桥挠度示意图

图4 活载作用下上承式拱桥下挠位移包络图

为加强桥面系和拱肋的薄弱位置,V形腹杆在设置时首先需保证有角点落在L/4、跨中、3L/4处,其次是尽最大可能利用其余角点对两者均匀约束,以提高线刚度。

另外,V形腹杆增设后结构的超静定次数会有所增加,若腹杆数量过多,则温度应力会迅速增加,对结构受力带来不利影响,且用钢量增大后结构的经济性会有所下降;若腹杆数量过少,则无法有效约束桥面系及拱肋,对结构刚度提高贡献不大,也不能有效减小梁端转角。因此,V形腹杆的数量需根据实际跨径及实际需要科学确定,以达到既使温度应力维持在较低水平又能有效减小梁端转角的最优目标。

2 本文拱桥梁端转角实验研究

2.1 实验桥结构布置及转换方法

实验桥跨径为10 m,桥面全宽1.08 m,矢跨比为1/5,拱轴线为悬链线,拱轴系数m=2.8,全桥均为钢结构,其中,除桥面板使用Q235钢外,其余构件均为Q345,实验桥结构布置如图5所示(单位为mm),实桥如图6所示。为方便本文拱桥与传统上承式拱桥之间进行结构形式转换,V形腹杆上特别设置了法兰盘,如图7所示,当螺栓拧紧时,腹杆参与受力形成本文拱桥;当螺栓松开,腹杆失效,此时为传统上承式拱桥。

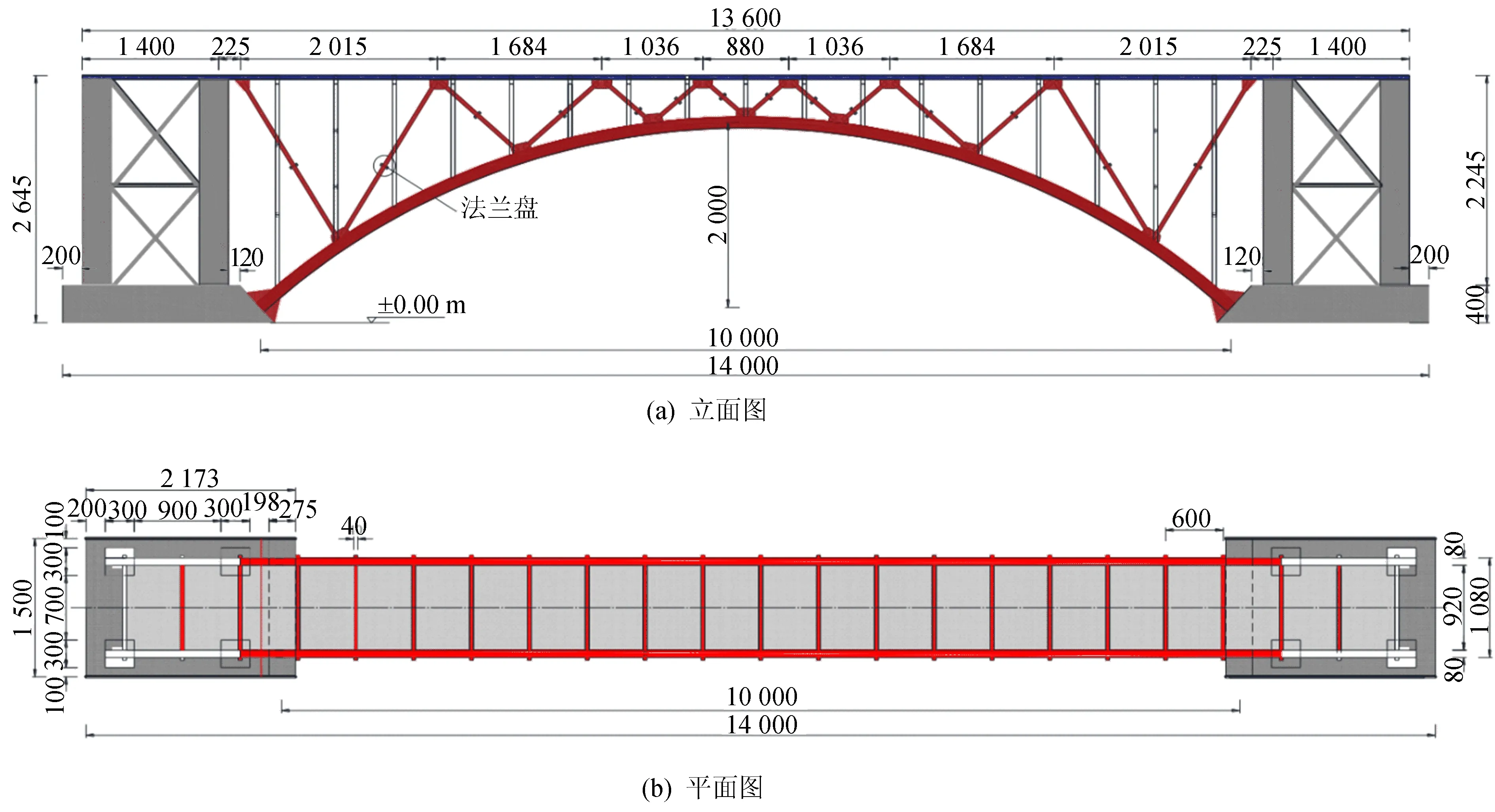
图5 实验桥结构布置

图6 实验桥实物图片

图7 法兰盘图片

2.2 实验目的与内容

实验仅研究桥台与桥梁主跨接驳处的最大梁端转角,目的是通过实验模拟上承式拱桥的活载工况,测试梁端转角,分析活载大小对梁端转角的影响。梁端转角实测值与有限元计算值互相佐证,确认数值分析的准确性和可靠性,以验证所提方法对减小梁端转角的有效性。

实验内容:通过在桥面布置水箱的方式进行加载,利用数显双轴倾角仪测量梁端转角,实验加载布置图如图8所示。加载分4级进行,每级加载时记录现场温度,以考虑温度变化对钢结构的影响。

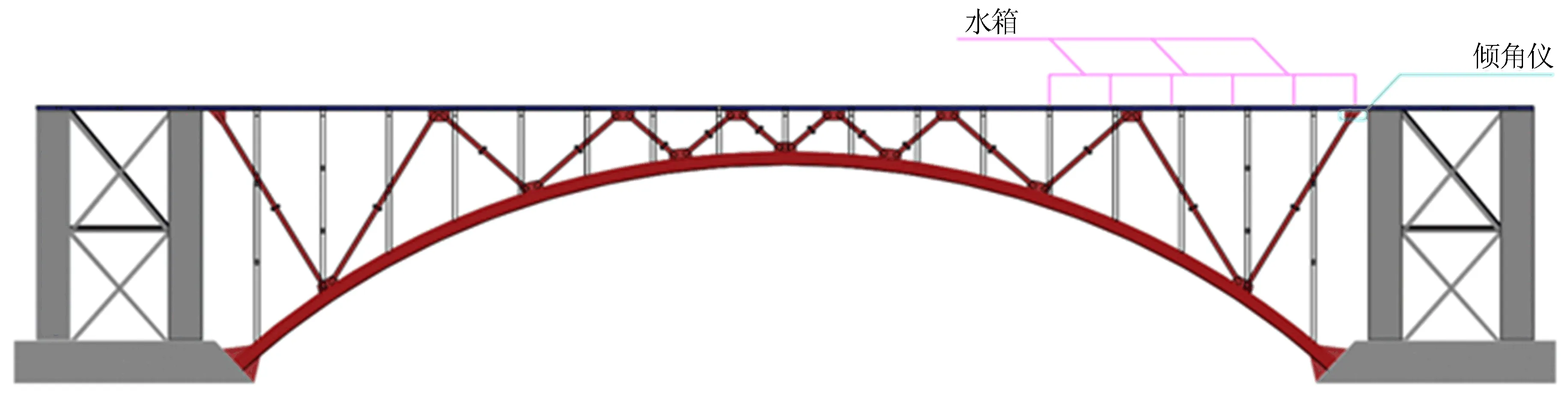
图8 实验加载布置图

2.3 有限元模型仿真分析

以实验桥为原型,利用通用有限元计算软件Midas Civil建立三维模型,传统上承式拱桥和本文拱桥的有限元模型如图9所示,模拟各级加载情况,计算梁端转角,具体结果见表1所列。表1中,θ11为传统上承式拱桥梁端转角;θ21为本文拱桥梁端转角;η0为变化率,η0=[(θ21-θ11)/θ11]×100%。有限元计算结果表明,增设V形腹杆后上承式拱桥的刚度大幅提高,故本文拱桥的梁端转角大幅减小。在同一级加载情况下,本文拱桥梁端转角的降幅均超过25%,可见,本文方法可有效减小梁端转角。

图9 有限元模型

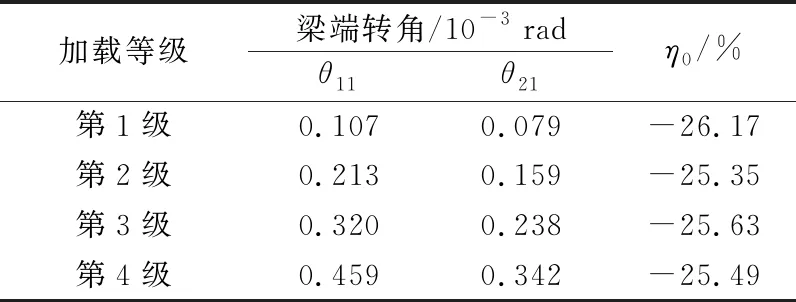
表1 梁端转角有限元计算结果

2.4 实验结果分析

实验所用的数显双轴倾角仪型号为TLL90S(精度可达0.001°),为减小实验误差,在梁端处横桥向共布置2个仪器,实验所测倾角取2个仪器读数的平均值,4级加载下实验桥梁端最大转角的实验结果见表2所列。表2中,θ12为传统上承式拱桥梁端转角;θ22为本文拱桥梁端转角;e1、e2为实验误差,e1=[(θ12-θ11)/θ11]×100%,e2=[(θ22-θ21)/θ21]×100%。

现场实验如图10所示。

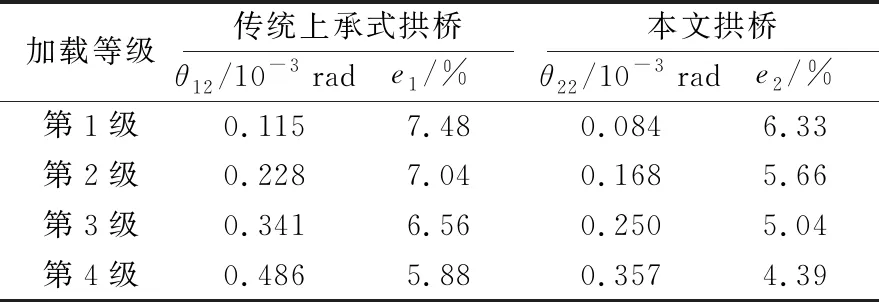
表2 梁端转角实验结果

由实验结果可知,实验值与有限元计算值相比,总体上有所偏大,但是误差较小,最大误差不超过7.5%,考虑到施工缺陷及模拟计算时对边界条件的理想化处理,实验数据具有较高的可信度。与传统上承式拱桥的实验值相比,本文拱桥每级加载下的梁端转角分别减小26.96%、26.32%、26.69%、26.54%。静载实验的结果充分验证了本文方法的有效性。

图10 现场实验

3 本文拱桥有限元分析

为进一步验证本文拱桥减小梁端转角的有效性,再以双线高速铁路拱桥为例,利用有限元软件建立三维模型,研究在传统上承式拱桥基础上增设V形腹杆后结构梁端最大转角和刚度变化,并将增设前、后所得结果进行对比分析,最后研究V形腹杆数量变化时温度作用下本文拱桥的最大应力及列车活载作用下的梁端转角。

3.1 结构布置

结构为连跨上承式拱桥,全长668 m,其中,每孔拱桥跨径为300 m,矢跨比为1/5,拱轴线为悬链线，拱轴系数m=2.5,桥面总宽20 m,立柱间距为30 m,拱肋和主梁均采用钢箱结构,桥面铺装以压力荷载的形式均布于桥面,全桥结构布置如图11所示(单位为m)。V形腹杆共28个,用钢1 756.7 t,约占总用钢量的11.5%,其余构件的参数及材料用量见表3所列。

图11 双线高速铁路拱桥全桥结构布置示意图

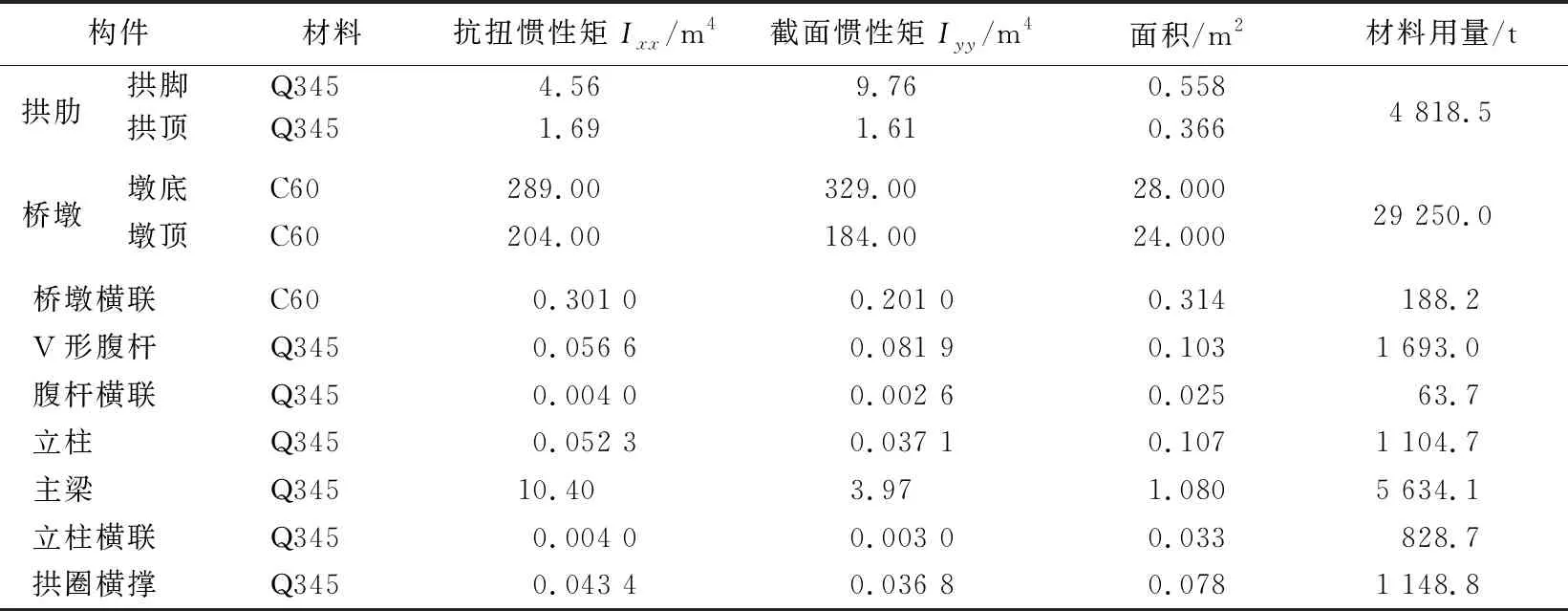
表3 双线高速铁路拱桥部分构件参数及材料用量

边界条件处理为:拱脚和墩台底部固结,立柱与桥面系间设弹性支撑。

3.2 梁端转角计算

有限元计算结果表明,所建模型各处的梁端转角均符合规范要求。在梁端处(入桥或出桥)以及两孔桥梁之间,本文拱桥的梁端最大转角分别比传统上承式拱桥减小了79.50%、26.61%、41.59%。

分析可知,仅需增加少量材料,传统上承式拱桥的梁端最大转角即可大幅减小,最大减幅可达0.46×10-3rad。由此可见,本文方法亦可用于改造梁端转角过大的现役铁路拱桥。

表4 双线高速铁路拱桥梁端最大转角有限元计算结果

3.3 结构刚度计算

本文拱桥梁端转角的减小得益于结构整体刚度的大幅提高,为验证理论的正确性,根据文献[8]要求,对结构在3个荷载组合下进行刚度研究:

组合Ⅰ:列车荷载。

组合Ⅱ:列车荷载+0.5×温度荷载。

组合Ⅲ:0.63×列车荷载+温度荷载。

其中,列车荷载为ZK活载,初始温度为15 ℃,升温最终温度为40 ℃,降温最终温度为-2 ℃。

在上述荷载组合下,本文拱桥与传统上承式拱桥主梁的最大挠度计算结果见表5所列。表5中,W1为传统上承式拱桥主梁位移;W2为本文拱桥主梁位移;η2为变化率,η2=[(W2-W1)/W1]×100%。

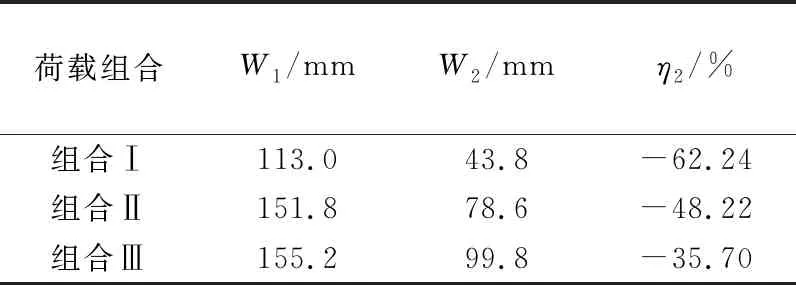
表5 双线高速铁路拱桥主梁位移有限元计算结果

本文拱桥单孔主梁上挠位移包络图及主梁L/4处位移影响线分别如图12、图13所示。

图12 本文拱桥主梁上挠位移包络图

图13 本文拱桥主梁L/4处位移影响线

有限元计算结果表明,与传统上承式拱桥主梁最大挠度相比,在荷载组合Ⅰ作用下,本文拱桥变形减少62.24%;在荷载组合Ⅱ作用下,本文拱桥变形减少48.22%;在荷载组合Ⅲ作用下,本文拱桥变形减少35.70%。此外,在荷载组合Ⅰ作用下,传统上承式拱桥单孔L/4跨处主梁上、下挠度(绝对值)之和为151.9 mm,而本文拱桥主梁上挠位移包络图中上挠值几乎为0,主梁L/4处位移影响线正面积值几乎为0,证明本文拱桥克服了现有拱桥结构体系的固有弊端。

分析可知,增加V形腹杆后,传统上承式拱桥的刚度得到大幅提高,且列车静活载在L/4跨处所产生的上挠度几乎为0。由此可见,本文方法对提高结构刚度有重要作用,因而可有效减小梁端转角。

3.4 结构温度响应分析

增设V形腹杆后整座桥实为一个大桁架结构,而腹杆的角度对桁架受力有着重要影响,且V形腹杆的个数直接关系到结构的超静定次数,因此也会对结构的温度应力产生影响。为分析结构在V形腹杆个数变化时的温度响应,在3.3节所建模型及其温度设置的基础上,设置V形腹杆个数分别为12、20、28、36,计算结构在温度作用下的最大应力以及列车活载作用下的梁端转角,具体结果见表6所列。

有限元计算结果表明,本文拱桥在温度作用下的最大应力随V形腹杆个数的增加而增大,且增幅明显;梁端转角随V形腹杆个数的增加而略有波动。

当V形腹杆个数由12增加到36时,升温作用下结构最大应力增幅高达38.0%;降温作用下结构最大应力增幅达38.1%。V形腹杆个数分别为20、28时,结构最大应力因温度作用发生的变化较小;个数为28时,本文拱桥的梁端转角相比于其余情形几乎为最小值。

分析可知,当V形腹杆个数为28时,本文拱桥的梁端转角几乎可达最小值,而结构的最大温度应力不大。经计算发现,此时V形腹杆与桥面系或拱肋所形成的三角形内角在45°～60°之间,因此,控制好V形腹杆的角度不仅可使结构的温度应力较小,也可有效减小梁端转角。

表6 V形腹杆数量变化时温度作用下本文拱桥的最大应力及列车活载作用下的梁端转角

4 结 论

本文提出了一种可有效减小大跨上承式铁路拱桥梁端转角的方法,通过实验及有限元分析得出以下结论:

(1) 梁端转角大幅减小。静载实验结果表明,传统上承式拱桥和本文拱桥在4级加载下的梁端转角实验值比计算值略大,但是误差在7.50%以内。本文拱桥与传统上承式拱桥的实验值相比,每级加载下的梁端转角分别减小26.96%、26.32%、26.69%、26.54%。

(2) 结构刚度大幅提高。增设V形腹杆后,引入桁式结构承担活载,可充分发挥其刚度大的优势,故结构的整体刚度得到有效提高,在列车活载作用下,主梁下挠位移值为43.8 mm,比传统上承式拱桥大幅减小。

(3) 拱桥的固有弊端被消除。由于整个结构形成了桁架,V形腹杆的存在使桥面系与拱肋得以连动,两者能更好地协同工作,因此在受半跨荷载作用时,另一侧不会出现上翘现象。

本文拱桥同时兼具拱结构和桁式结构的优点,其良好的刚度特性可有效减小梁端转角,对保证列车行驶安全性与舒适性有很大帮助,因而特别适用于大跨高速铁路桥梁。