煤矿开采矿井涌水量预测方法现状及发展趋势

2020-12-04王晓蕾

科学技术与工程 2020年30期

关键词：涌水量含水层矿井

王晓蕾

(1.吕梁学院矿业工程系，吕梁 033000；2.煤矿机械装备维护与检测试验吕梁市重点实验室，吕梁 033000)

随着中国煤矿开采深度的逐渐增大，开采已完全进入深部开采阶段[1-3]，深部开采面临众多的地质问题。其中涌水量大小关系煤矿安全生产问题[4-5]。特别是华北煤田面临深部奥灰水的威胁，其涌水量大小是煤矿安全生产的重要因素[6-8]。

矿井涌水是煤矿安全生产中的重大隐患[9]。矿井涌水会阻碍煤矿生产，特别是导致透水事故的发生[10-11]，而准确预测涌水量是防止突水事故发生的重要因素[12-13]。

矿井涌水量的准确预测对于煤矿安全生产具有重要意义。为此，总结了矿井涌水量预测的技术现状，分析了涌水量预测存在的不足，针对存在的问题，提出了未来矿井涌水量预测发展趋势。

1 水文地质比拟法

水文地质比拟法也称为类比法[14]，是根据地质情况[15]、水文条件[16]、开采方法[17]等基本类似的矿井涌水量的数据预测新矿井的涌水量[18-19]，该方法必须保证老矿井有长期观测的涌水量数据[20]，保证涌水量与影响因素之间的关系的可靠性[21]。该方法计算简单，便于操作，但是计算精度较差，是近似的计算方法[22]。

(1)

式(1)中：Q表示矿井预计的涌水量；F表示预计水平开采面积；S表示煤矿开采过程中的水位降低值；S0表示煤矿未开采情况下的水位；Q0表示矿井实测过程中的涌水量；F0表示生产矿井中的实际面积。

段东伟等[23]采用水文地质比拟法对蒙陕矿区纳林河二号矿井涌水量进行了预测。

纳林河二号井田位于鄂尔多斯境内(图1)，矿井生产能力800×104t/a，主采3-1号煤层，地表是风积沙进行覆盖，属于高原大陆性气候，干燥少雨，煤层以上属于河流相沉积，顶板含水层较厚，水压较高。

图1 矿区位置Fig.1 Location of mining area

31121工作面长、宽分别是2 640、300 m，煤层厚度6.5 m，为近水平煤层，顶板主要为泥岩、细砂岩，底板为砂质泥岩。

工作面上方包含多个含水层，其对工作面有充水条件，含水层如图2所示。

图2 含水层Fig.2 Aquiclude

依据工作面水文地质特征，工作面充水通道可以有多重，如图3所示。

图3 充水通道Fig.3 Water filling channel

工作面充水强度在掘进未有突水现象，涌水量较小，其变化特征如图4所示。

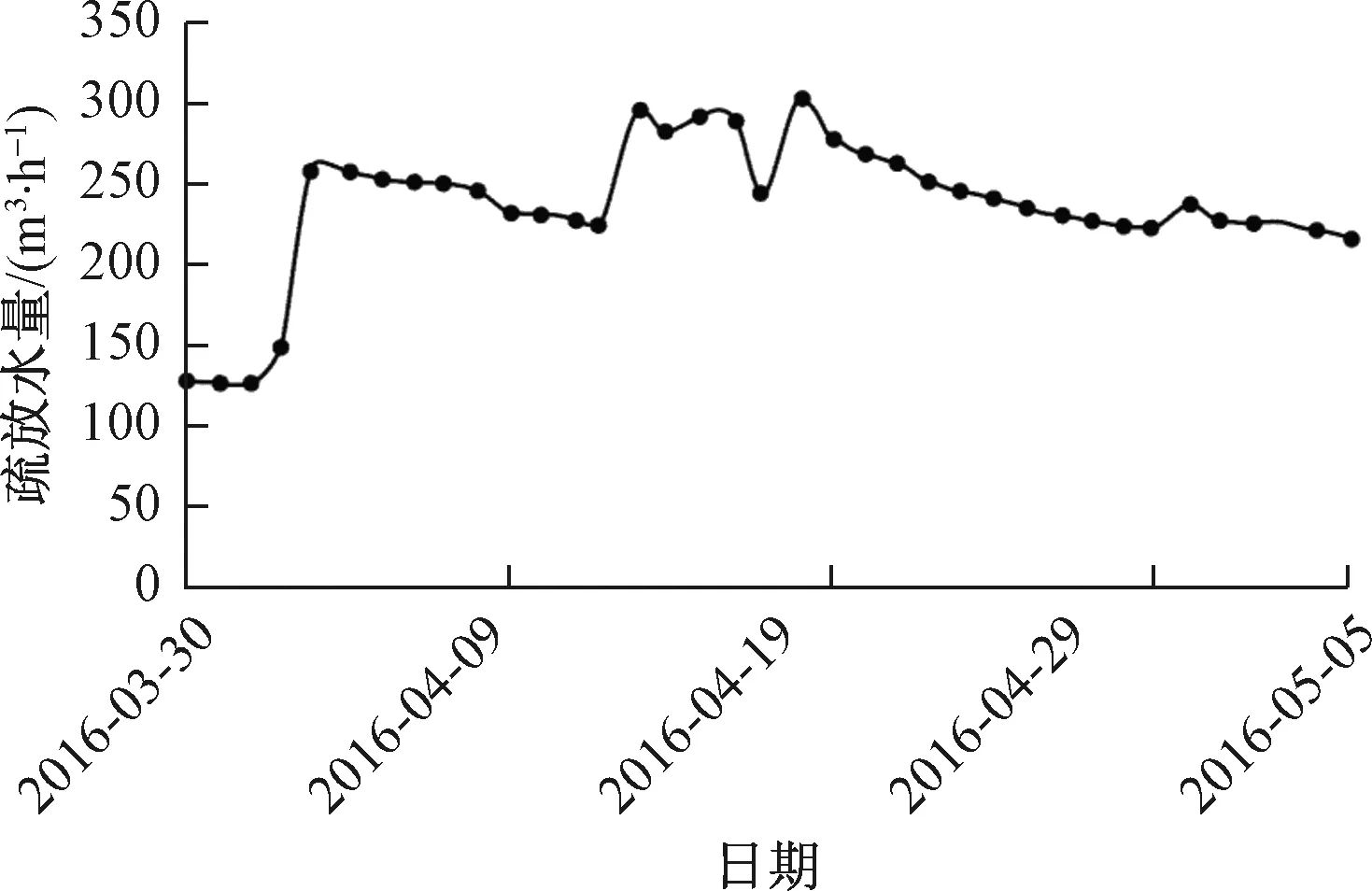
图4 顶板水疏放涌水量Fig.4 Water discharge from roof

依据工作面顶板含水层、充水通道以及充水强度特征得出工作面的预计涌水量如图5所示。

图5 涌水量预测曲线Fig.5 Forecast curve of water inflow

根据工作面回采过程中涌水量监测数据对比涌水量预测曲线(图5)，涌水量预测数据与实际误差小于6%，对于煤矿涌水量预测具有一定借鉴。

杜铝钢[24]采用该方法对生辉煤业涌水量进行了预测；黄建飞等[25]采用该技术对龙门煤矿矿井涌水量进行了研究；和祥等[26]采用该法对涌水量进行了分析；杨军等[27]采用该技术对沙沟岔煤矿涌水量进行了分析；翁莉等[28]预测了涌水量；任廷福[29]对新桥煤矿涌水量进行了分析。

2 回归分析法

回归分析法是一种数理统计计算方法[30]，它是根据矿井涌水量与涌水量影响因素之间的关系建立回归方程[31]，通过建立涌水量与影响因素之间的关系预测涌水量，其要求必须要有足够多的数据[32]，要以定性机理进行分析，统计要选取反应充水条件的因子[33]。

(2)

式(2)中：x1，x2,…,xk表示线性回归因子；y表示观测值；b0,b1,…,bk表示线性回归系数；ε表示随机误差；σ2表示残差。

李孝朋等[34]采用多元回归分析对矿井涌水量进行了预测。山西大同某矿区一盘区煤矿资源已采完，立即开采二盘区，两个盘区同属于一个矿区，其地质特征、水文条件、开采工艺相同，拥有完整的一盘区水文资料，通过多元回归方法研究二盘区矿井涌水量。

采用SPSS数学分析软件对矿井涌水量影响因素进行分析，选取掘进尺度、煤炭产量、开采厚度、采空区面积作为影响涌水量的因子。其相关性和显著性如图6所示。

由图6可知，掘进进尺、采空区面积、煤炭产量对于煤矿矿井涌水量显著性较低，线性关系较差。

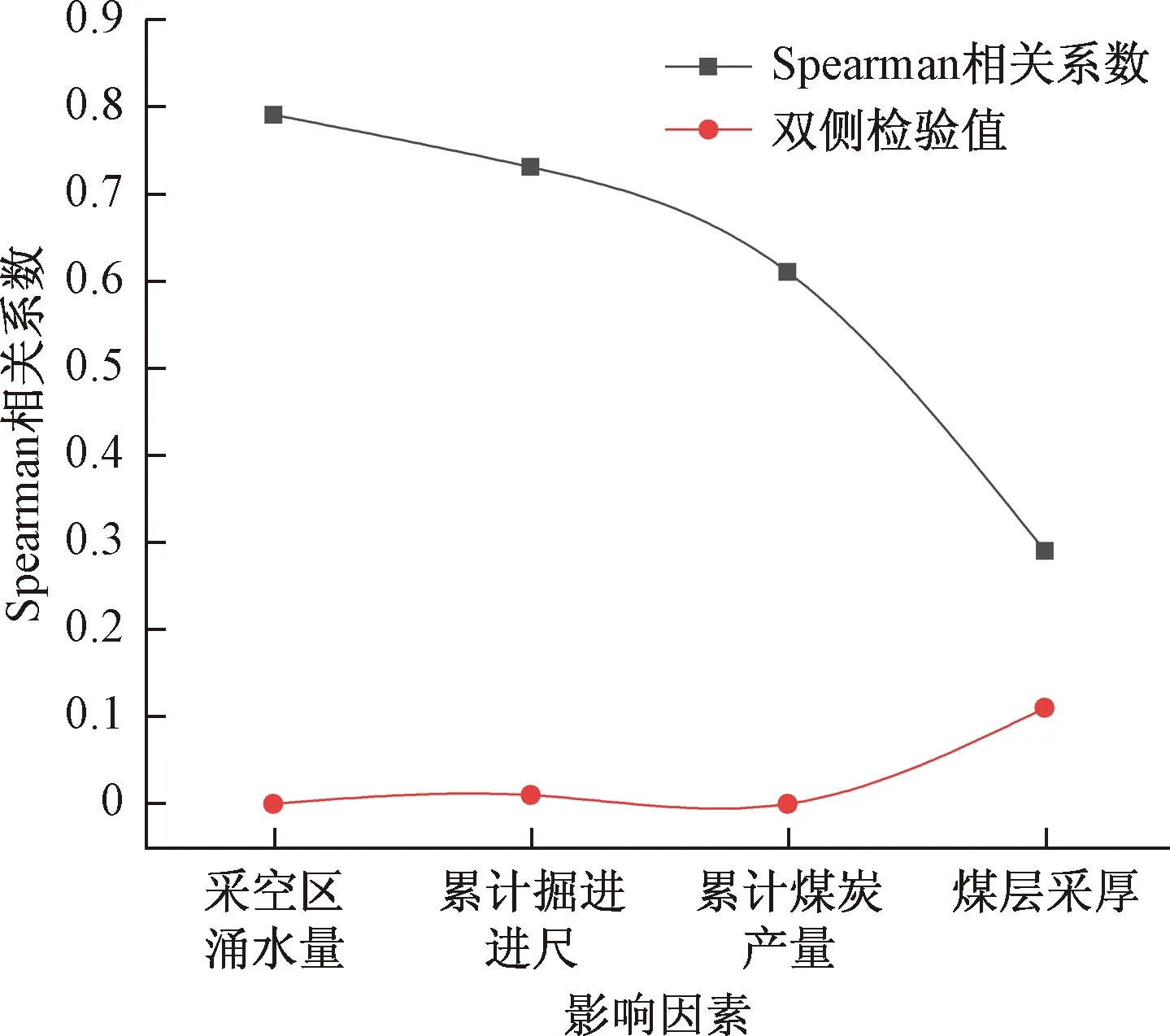
图6 影响因子相关性及显著性Fig.6 Correlation and significance of influencing factors

对涌水量和采空区面积、累计进尺、产量的散点图进行拟合，得出3个影响散点图(图7)。

图7 影响因子与涌水量散点图Fig.7 Scatter plot of influential factors and water inflow

利用MATLAB数学软件对影响因子进行非线性拟合，得出3个函数，通过计算影响因子与涌水量的数值，得出矿井涌水量(图8)。

图8 预测值与实测值对比Fig.8 Comparison of predicted and measured values

由图8可知，根据涌水量预测值对比涌水量实测值，得出不同采空区面积下的涌水量误差分别是-12.44%、16.72%、13.77%。误差值均在允许范围内，由此可知，该方法对于涌水量预测准确度较高，对于类似矿井可用该方法进行预测。

魏真等[35]采用回归分析法对徐州某矿不同影响因素与涌水量关系进行了分析，建立了涌水回归模型；江峰等[36]采用回归方法对隧道涌水量与降水量建立了回归方程关系，并根据实际情况对回归方程进行了检验。

3 模糊数学法

模糊评价法是一种基于模糊数学的安全评价法，是根据模糊数学的隶属度理论将定性化评价转化为定量化评价[37]，是一种对多因素制约事物或对象做出的总体评价，其结果清晰明了，能够较好地评价难以量化的问题[38]。

模糊评价模型是对于多因素、多层次的庞大评价系统[39]，通常需要建立多层次评价模型进行分析，对于多层次而言，最基本的要建立单层次评价子集，将各个子集作为新节点进行多层次评价，其是多层次评价的基础[40]。

依据评价的小组信息将上评价信息作为下一评价的基础，一般情况下是单个元素对矩阵评价的一个向量R(ui)，i=1,2,…,n，对于任何一个评价都可用以下矩阵来表示[41]。

Ri=[R(u1),R(u2),…,R(un)]

(3)

对于给定评价因素的权重可表示为

Ai=[A11,A12，…，A1n]

(4)

依据多层次评价信息得出其评价结果为

Ri=Ai⊗Ri

(5)

式(3)～式(5)中：Ri表示评价矩阵；R(ui)表示评价向量；Ai表示权重矩阵；A1i表示权重向量；⊗表示模糊数学计算符号；i=1,2,…,n。

姬亚东[42]采用模糊数学法对塔然高勒煤矿西一盘区3-1煤层顶板含水层涌水危险性进行了预测，对各个涌水区危险性进行了综合评价，分为4个等级。

该矿位于东胜煤田塔然高勒矿区中北部，矿区内主要包含三层煤，煤层平均厚度6.5 m，主采3-1号煤层，位于延安组第二岩段。全区域裂隙发育，煤层平均厚度3.71 m，顶板主要为泥岩和砂岩，局部为粗细砂岩。含水层厚度等值线如图9所示。

图9 含水层厚度等值线图Fig.9 Contour map of aquifer thickness

根据对矿井地质特征、水文资料以及顶板特征，同时利用顶板钻孔资料，对含水层涌水影响因素进行相关性分析，得出其顶板含水层富水性影响因素，如图10所示。

图10 顶板富水性影响因素Fig.10 Factors affecting water richness of roof

根据影响因素对含水层涌水量的定性影响结合矿井地质特征，量化各影响因素的标准，得出各影响因素的权重，如图11所示。

图11 影响因素权重图Fig.11 Weight chart of influencing factors

以A′区为例，根据A′区各影响因素的平阿基标准，对其计算模糊关系矩阵RA′，将权重向量A与模糊关系矩阵RA′相乘得到权模糊算子BA′。

(6)

(7)

(8)

按照最大隶属度关系，得出BA′的值为0.56，属于安全区，同理得到其他区安全性如图12所示。

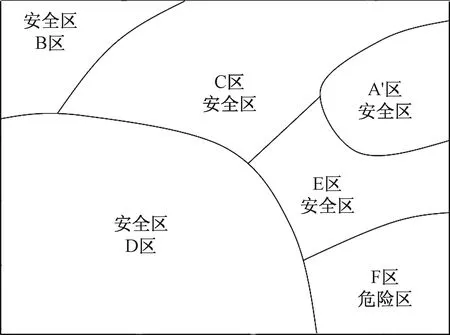
图12 涌水量安全区分图Fig.12 Safety division of water discharge from roof

涌水量区分图(图12)与实际开采情况吻合，该预测方法对于涌水量预测具有较好效果。

仝联合[41]采用模糊数学法对瑞隆矿17065工作面涌水量进行了预测；刘伟韬等[42]采用模糊数学法综合多种因素对矿井涌水量进行了分析，为制定防水措施提供依据。

4 灰色理论法

灰色理论法是将一个随机变量看成一定范围内变化的灰色的量[43-44]，其随机变化过程是在一定范围内变化的，起变化过程是与时间相关的。主要是通过对部分已知信息对其进行生成与加工[45]，提取有价值的信息[46]，实现对系统以及变化规律的有效预测[47-48]。

范军平等[49]采用灰色理论模型对义马煤田中部矿井涌水量进行了研究，建立了预测模型。

济宁三号煤矿主采3号煤层，在开采的过程中发生多次涌水事故，最大突水量可达533.84 m3/h，为了保证工作面安全，要对其顶板涌水进行预测。

对2002—2014年矿井涌水量数据进行处理，有：

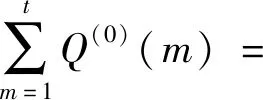
(351.6,382.4,…,409.1)

(9)

式(9)中：Q(1)(t)表示涌水量预测序列；t表示时间，年；Q(0)(m)表示每年涌水量。

原始数据的光滑程度影响预测模型的准确度，越光滑准确度越高，检验公式为

ρ(t)=Q(0)(t)/Q(1)(t-1)

(10)

式(10)中：ρ(t)表示涌水量预测准确值。

根据计算当t>2时，得到的数值均小于0.5，其随机性较强，光滑性较好，得出预测数据越准确。

对式(9)进行一次累加得

ω(1)=(849.7,916.5,…,2 704.55)

(11)

对式(11)得出的白化方程进行处理，得到灰色理论公式为

Q(0)(t)+uω(1)(t)=v

(12)

式(12)中：u、v表示依据实际情况确定的参数。

根据灰色理论计算得出参数值：u=-0.045 19，v=302.05。

其预测公式为

(13)

利用预测公式[式(9)～式(13)]预测2002—2014年矿井涌水量，结果如图13所示。

图13 预测值和实测值对比Fig.13 Comparison of predicted and measured values

对预测值和实测值进行分析，得出该模型的平均残差较小，仅为0.095，根据预测精度计算公式得出该模型的准确度为90.5%，精确度等级为优秀，依据此模型预测2015—2017年涌水量如图14所示。

图14 2015—2017年涌水量预测值Fig.14 Water inflow forecast for 2015—2017

依据2015—2017年涌水量预测值，采区相应的防治水策略，为矿井水灾害防治以提供了科学依据，保证了工作面的安全生产。

朱愿福等[50]基于灰色理论，提出了一种新型的矿井预测模型，这种新陈代谢组合模型能够预测综合评价的指数，并通过对靳各庄矿涌水量进行了验证。

5 BP人工神经网络

BP(back propagation)人工神经网络是一个非线性系统，它是由大量的神经元构成的系统[51]。它在一定程度和层次上模仿人的大脑神经系统进行信息的处理、选择、储存以及检[52]，其具有学习、记忆以及计算等智能处理的相关功能。矿井涌水是一个非常复杂的水文地质综合体，因此，很难准确地采用数学模型进行有效的涌水量进行预测，而建立一个涌水量与充水因素是一个可行的方法，该理论就很好地体现了其优点[53]。

当样本提供给网络后，系统会随机生成权值，并进行重复计算并传输，直到输入结果，将理想结果与计算结果进行对比分析，确定其阈值。随着误差不断纠正，直到满足条件训练结束[54]。

其输入模式传播按照随机给定的权值和阈值，对学习样本进行计算输出值，输入值到隐含层的计算公式为

(14)

隐含层到输出层的计算公式为

(15)

式中：ai表示计算过程中第i个输入；b1j、b2j分别表示隐含层、输出层的阈值；f表示计算过程中的传递函数；Hidden(j)表示隐含层中第j个输出值；Wij、Wjl分别表示隐含层、输出层的权值。

对于输出误差逆传播，当输出节点得出实际值后，如果这些数值与实际情况值相差较大，就要重新确定权值和阈值，按照程序进行重新计算，保证其差值在允许范围内。

假设绝对误差的均方值计算公式为

(16)

对其权值进行调整，计算公式为

ΔW=β(-gradvEk)

(17)

李哲等[55]以陕北柠条塔煤矿为试验矿井，该矿中没有大断层、褶皱，地质构造属于简单。主采2-2号煤层，其顶板为砂岩，富水性中等，该矿发生过一次突水事故，其矿区涌水量为1 157 m3/h，为了保证其工作面安全生产，对其富水性进行评价。选取矿井地质、水文地质、含水层性质、取芯率、风化程度、渗透系数作为影响富水性的因素。选取25个水文孔资料作为学习样本。根据钻孔资料以及影响因素进行定量化处理，采用GIS软件和Surfer软件进行定量化分析，作出其分析图，量化后数据不同导致其影响范围存在很大差别。因此要对某些数据进行归一化处理，将其统一到一个数量级别上。

借助MATLAB数学软件进行分析，使用25个样本作为基础参数进行训练，当训练4 728次后，误差值降低到设置值范围内，得出多组参数，选取其中的5个再次作为训练样本进行训练，得出检验样本和预测结果，如图15所示。

图15 理想值与预测值对比图Fig.15 Comparison of ideal and predicted values

由图15可知，误差最大值为2.1%，在允许范围内，该模型能够较准确的预测富水性。

凌成鹏等[56]采用神经网络法对韩桥煤矿涌水量进行研究，得出了短期预测模型，预测结果与实际值吻合性较好。

6 时间序列分析法

时间序列分析法主要包含两部分[57]，一部分是时域分析[58]，另一部分是频域分析[59]。时间序列分析法采用一系列具有科学理论为依据的动态数据处理方式[60]，帮助人们通过合理的分析获得动态数据，从而更好地掌握客观现象的本质[61]，进一步认识事物，预测未来[62]。其中时域分析是通过对数据进行处理建立模型[63]，采用线性最小方差预测未来[64]。频域分析是可以预测涌水量的周期性，判断涌水量的影响因素，同时，它还可以研究涌水量影响因素的权重性[65]。

涌水量预测模型首先建立回归模型，建设{Xt}是具有表示性的时间序列，其样本的长度为M，假设以年、月、日为观测时间，得出模型[66-67]：

Xt=φ1Xt-1+φ2Xt-2+…+φjXt-j+at

(18)

式(18)中：Xt表示矿井水涌水量；φj表示自回归参数；at表示影响矿井水涌水量的各种因素。

经过分析得出最终模型：

(19)

式(19)中：p表示矿井涌水量预测模型阶数。

曲兴玥等[68]采用时间序列对青龙煤矿矿井涌水量进行了研究，发现青龙煤矿主采16、17、18共3个煤层，煤层总厚度超过127 m，矿井开采过程中发生过多次突水事故，给矿井安全生产带来了威胁，突水的最大涌水量为350 m3/h，其突水来源主要市采空区积水、顶板含水层水。

基于该矿的最大涌水实测为基础，采用SPSS数学软件，对涌水量预测进行时间序列建模，如图16所示。

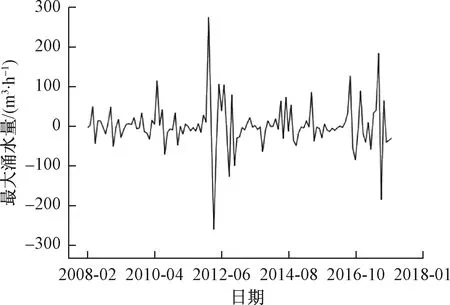
图16 涌水量一阶差分Fig.16 First order difference in water inflow

对原始序列建立时间序列模型，得出青龙煤矿最大涌水量预测方程：

Δyt=0.588Δyt-1+0.998Δyt-1+342.738

(20)

式(20)中：Δyt、Δyt-1分别表示t年和t-1年的煤矿最大涌水量。

依据时间序列模型拟合效果如图 17所示。由图17可知，涌水量稳定时，预测精度较高，当波动大时，预测精度低，因此，涌水量呈非线性。

图17 拟合效果Fig.17 Fitting effect

基于时间序列对其分解，综合季节变动、不规则变进行分析，重新拟合得出新的涌水量预测模型：

y=-0.000 009x5+0.001 3x4-0.067 4x3+1.283 4x2-6.540 6x+117.92,

x=1,2,…,55

(21)

式(21)中：x表示月数，2011年1月为1，以此类推递加，得出拟合图如图18所示。

由图18可知，该模型在5次平移后，其预测趋势与实际相差较小，预测准度高，采用该模型对最大涌水量进行预测，得出预测数据如图19所示。由图19可知，分解预测模型预测的涌水量与实际涌水量吻合度较高，该方法具有较高的预测精度。

图18 5次平移趋势拟合图Fig.18 Five-time translation trend mapping

图19 分解预测模型结果Fig.19 Decomposition prediction model data

夏克勤[69]采用时间序列分析法对鱼田堡煤矿矿井涌水量进行了分析，对降水量与涌水量及渗透系数加权进行了研究，建立了预测模型，该模型预测涌水量是可行的；安欣等[70]采用时间序列分析法对东欢坨矿矿井涌水量进行了分析，建立了预测模型，并进行了涌水量预测，误差较小，预测精度较高，能够很好地满足工程需要，其预测短期涌水量是可行的。

7 数值模拟法

数值模拟法采用的是偏微分方程表示矿井实际水流系统的一种模型预测方法，其预测值没有精确值，只是一个近似值，可称为数值解[71]。它是运用计算机系统采用数值分析的方法来求解模型的解，通过计算机模拟实际系统的运行状态。目前主要有有限元和有限差分两种数值模拟方法，通过计算机软件进行实现[72]。

李贵仁等[73]采用数值模拟方法对刚果铜矿进行了涌水量预测。该矿位于刚果，其属于加丹褶皱—推覆构造带的一部分，其面积约为140 km2，其最大厚度可达1 000 m，其构造发育较高。整体呈东北向分布，断裂面方向为南，其倾角平均为30°，根据相关特点可知，其构造极其发育，为地下水运移提供条件，水文地质情况如图20所示。

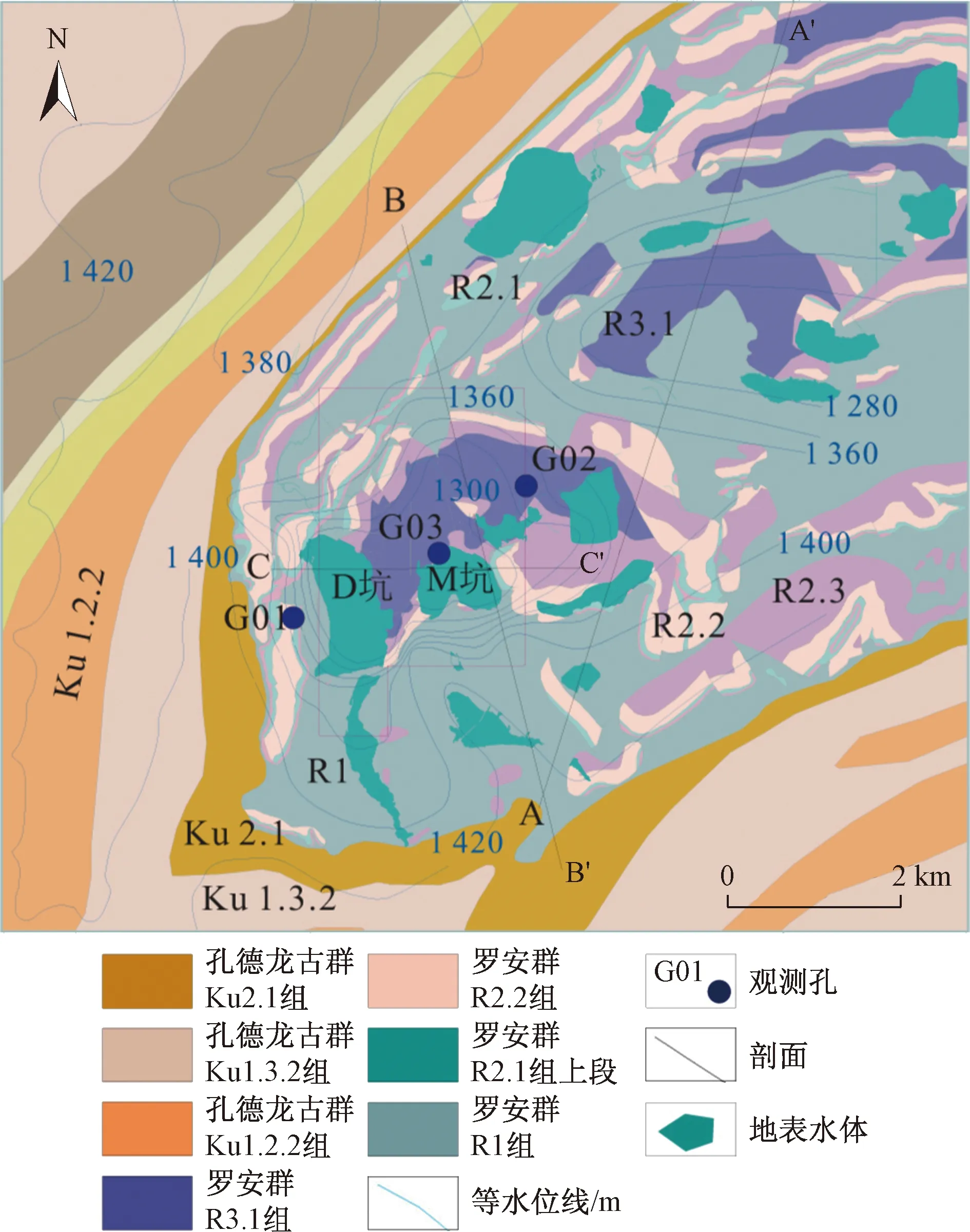
图20 水文平面Fig.20 Hydrological plans

采用VM数值模拟软件对涌水量进行预测，其流场拟合如图21所示。

图21 流畅拟合图Fig.21 Smooth fitting diagram

结合地下水动态平衡系统和降水渗透系数对矿井涌水量进行预测。

骆祖江等[74]采用数值模拟法对大同矿区地下水进行了模拟，预测了8214、8216工作面的涌水量，该方法将涌水量预测与回采工作面进度有机结合起来，其预测结果更能反映实际情况。

8 大井法

煤矿生产过程中，要对含水岩层进行排水工作，在整个排水过程中，随着排水的进行，其水位不断下降[75]，当下降到一定程度后其水位呈稳定状态，该状态可称为稳定流状态[76]。该状态是以矿井为中心形成的地下水辐射渗流场满足地下水稳定井的条件，而实际的矿井是一个不规则的形状，为了便于研究，理论上认为是一个井在工作，整个工作面的用水是一个井在涌水，采用裘布依稳定流方程进行预测[77]。

潜水完整井的矿井涌水量计算公式为

Q=1.366K(2H-S)S/lgR-lgr

(22)

承压水完整井的矿井涌水量计算公式为

Q=1.366KMS/lgR-lgr

(23)

潜水与承压水完整井矿井涌水量计算公式为

Q=1.366K(2HM-M2-h2)/lgR-lgr

(24)

式中：Q表示矿井涌水量；K表示矿井含水层的渗透系数；M表示矿井含水层厚度；H表示矿井含水层的水头高度；h表示矿井排水后水头高度；S表示排水的降深；R表示漏斗影响半径；r表示大井法的引用半径。

陈冲等[78]采用大井法对煤矿涌水量进行了预测，在对大井法分析的基础上，详细阐述了大井法对煤矿的应用，依据不同的含水层及冲水条件进行了涌水量预测，选取参数如表1所示，矿井边界构造如图22所示。

图22 矿井边界构造Fig.22 Mine boundary structure

表1 选取参数Table 1 Select the parameter

将相关参数代入式(7)，综合矿井边界构造特征得出矿井开采3号煤层时的涌水量为2 928.4 m3/h。揭露同一矿区本煤层时，其水文、开采、地质条件类似，其涌水量为130 m3/h(开采面积6.2 km2)，该矿的正常涌水量为215 m3/h(开采面积10.3 km2)，其预测结果与实际相近，证实了预测的准确度。

罗安昆等[79]采用大井法对亭南矿和胡家河矿两个工作面涌水量进行了预测，验证涌水量的合理性。丛利等[80]采用大井法对门克庆煤矿首采工作面回采后涌水量进行了分析，把不规则的影响边界看成一个大井，基于井下群孔放水试验预测了工作面的涌水量。

9 存在问题及发展趋势

9.1 存在问题

传统的水文地质比拟法计算粗糙，是一种近似的矿井涌出量计算，精度不够；回归分析法对比新建矿井无法预测，其首先必须有足够的数据，同时其相关因子不易选择；模糊数学法虽然考虑了多种影响因素，但其不能确定未来涌水量的趋势；灰色理论法适用于涌水量稳定的矿井，对于涌水量变化较大的矿井预测结果不理想；时间序列分析法其对原始数据要求较高，不易进行预测；数值模拟法是一个近似解，对于涌水量要求精度高的矿井不适用；大井法偏离了实际原型，预测结果不够准确。