基于扩展单元插值法二维弹性问题的边界元法分析
2020-12-04钟玉东侯俊剑谢贵重张见明
钟玉东,侯俊剑,谢贵重,张见明,李 源
(1.郑州轻工业大学机电工程学院,河南省机械装备智能制造重点实验室,郑州 450000;2.湖南大学机械与运载工程学院,长沙 410082;3.河南师范大学计算机与信息工程学院,新乡 453007)
边界元法是基于格林公式和问题的基本解将控制微分方程转化为边界积分方程的一种数值方法[1-2],已经在实际工程问题的求解中得到了应用。相比有限元法[3],边界元法具有降维和计算精度高的优势,特别是针对裂纹问题、接触问题、弹性动力学等对应力精度要求较高问题的求解[4-7]。有限元法的方程是一种弱形式,对试函数有C0连续的要求。边界元法则不要求试函数连续,对网格节点没有连接性的要求,再加上不需要处理内部网格的特点,很大程度降低了网格划分的困难。另外,由于基本解自动满足无穷远处的边界条件,边界元法可以自然地求解无限域和半无限域问题[8-9]。
目前,边界元法主要有两种数值实现方式,一种是使用连续单元,另外一种是使用非连续单元。连续单元直接把节点配置在单元的几何顶点上,同等单元阶次下要比非连续单元的自由度少,计算量小。但由于几何角点处的法向量方向不唯一,求解面力、热流量等场变量时存在一些困难[10-11]。非连续单元把节点配置在单元的内部,克服了连续单元处理角点的困难,为数值实现过程提供了方便,既可以简化系统方程,又降低了网格生成的难度,但在同阶次下的自由度要比连续单元要多,计算量大。另外,由于几何角点处的场变量要通过内部点外插得到,在处理多域界面问题时,会导致场变量求解的不精确[12]。
为了统一连续和非连续单元,采用一种新型的扩展单元插值法[13]来求解二维线弹性问题。扩展单元是在非连续单元的两端和边界上添加虚点,继承了连续和非连续单元的优点,同时克服了它们存在的缺点。扩展单元有两套形函数,一种是RawShape形函数,由内部的源点构造。另外一种形函数是由源点和虚点一起构造,称为FineShape。边界积分方程中的物理变量通过FineShape插值,但系统的矩阵方程只在源点处配置。RawShape是用来构建源节点和虚节点之间的关系,根据这一关系可以通过源节点来消掉虚节点的自由度,以达到不改变系统方程自由度前提下,提高插值精度的目的。
1 扩展单元插值法
1.1 扩展单元
扩展单元是由源节点和虚节点组成,图1给出了3种不同类型的扩展单元,其中图1(a)为常值扩展单元,图1(b)为线性扩展单元,图1(c)为二次扩展单元,相应的形函数如式(1)~式(3)所示。

图1 3种不同类型的扩展单元Fig.1 Three kinds of expanding elements
(1)
(2)
(3)
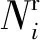
1.2 扩展单元插值法的具体实现过程
在扩展单元中虚节点并不作为源节点出现在最终的系统方程中,如何得到虚节点的值就显得尤为重要。以图2的四边形模型域来介绍一下不同条件下虚节点值的计算方法。
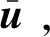

图2 扩展单元插值法具体实现实例Fig.2 The example of the concrete implementation of the expanding element interpolation method


(4)
(5)
对于连续场(位移边界条件),可以采用式(6)、式(7)求得。
(6)
(7)
所有虚节点值得到之后,边界积分方程中的物理变量就可以通过扩展单元的FineShape来插值了,如图2中右边那条边的位移和面力可以通过式(8)插值得到。
(8)
式中:u和t分别为所有节点的位移和面力。
将式(5)~式(7)代入式(8)中,可以得到扩展单元插值法所用的最终表达式,如式(9)所示:
(9)
利用扩展单元插值计算时,虚节点的值并不作为独立的变量,它是由已知边界条件或者由和它相连接的邻近单元的RawShape外插得到。虚节点的自由度是可以通过和源点的关系凝集掉,最终的系统方程只在源点处配置,方程的大小并没有发生变化。另外,通过在几何顶点处布置两个虚点(针对二维问题,两个虚点分别属于和它两连的两个单元),无论是连续场还是非连续场都可以得到精确的估计。
2 边界积分方程的数值离散
弹性问题的边界积分方程即式(10),求解该问题时,首先需要对该问题的方程进行数值离散,将边界Γ离散为ne个扩展单元,每一个扩展单元有nα个节点(包括源节点和虚节点),式(10)可以离散为式(12)的形式

(10)

(11)

(12)

Hu=Gt
(13)
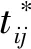
(14)
若整个计算域中包含n个源点和m个虚点,将矩阵中的元素按已知和未知的边界条件来区分,式(13)可以表示为
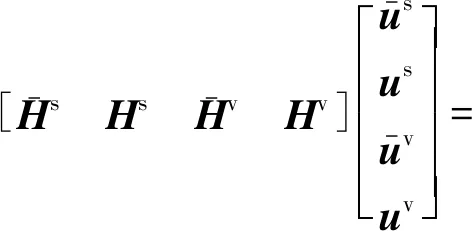
(15)
(16)
式(16)中:Nr表示扩展单元的RawShape形函数,将式(16)代入式(15)中,式(15)可进一步写为
Ax=f
依照多媒体技术目前在高中物理教学中的教学现况来说,高中物理多媒体技术的课堂质量需要快速地提升,将传统老旧的教学模式进行改革创新.把多媒体技术资源合理的运用到高中物理教学中的最终目标是利用现代教育技术配合高中物理教学并搭配传统的教学方式,更好的呈现教与学的完美融合.伴随着现代信息技术的迅速发展,坚信多媒体技术在高中物理教学领域中能够拥有更辽阔的教育应用前景.
(17)
式(17)中:矩阵A、向量x和f′分别表示为
(18)
由式(17)、式(18)可知,线性系统方程系数矩阵的大小和用传统非连续单元插值时的一样,且和虚节点有关的变量在整个系统矩阵中并没有出现,因此系统方程的自由度大小并没有改变。所以,本文方法提高插值精度的同时并没有改变系统方程的自由度大小。
3 数值算例
为了验证扩展单元插值方法在求解弹性问题时的计算精度和收敛性,给出了两个算例,并与相应的参考解进行对比。为了估算本文方法的计算误差和收敛性,给出了一种相对误差Eerror的估计公式,如式(19)所示:
(19)

3.1 悬臂梁
在本例中,将扩展单元插值法应用于悬臂梁问题,悬臂梁几何结构如图3所示。自由端收到y方向载荷P的作用,相应的位移和应力的解析解[14]分别为
(20)
(21)

A、B、C、D表示悬臂梁的4个顶点图3 悬臂梁结构Fig.3 The structure of cantilever beam

从图4~图7可以看出,采用扩展单元插值法得到的计算结果,无论是精度还是收敛性都要比传统连续和非连续单元的要高。

图4 AB边上y方向的位移uy的收敛性Fig.4 Convergence rates of the displacement uy along the edge AB
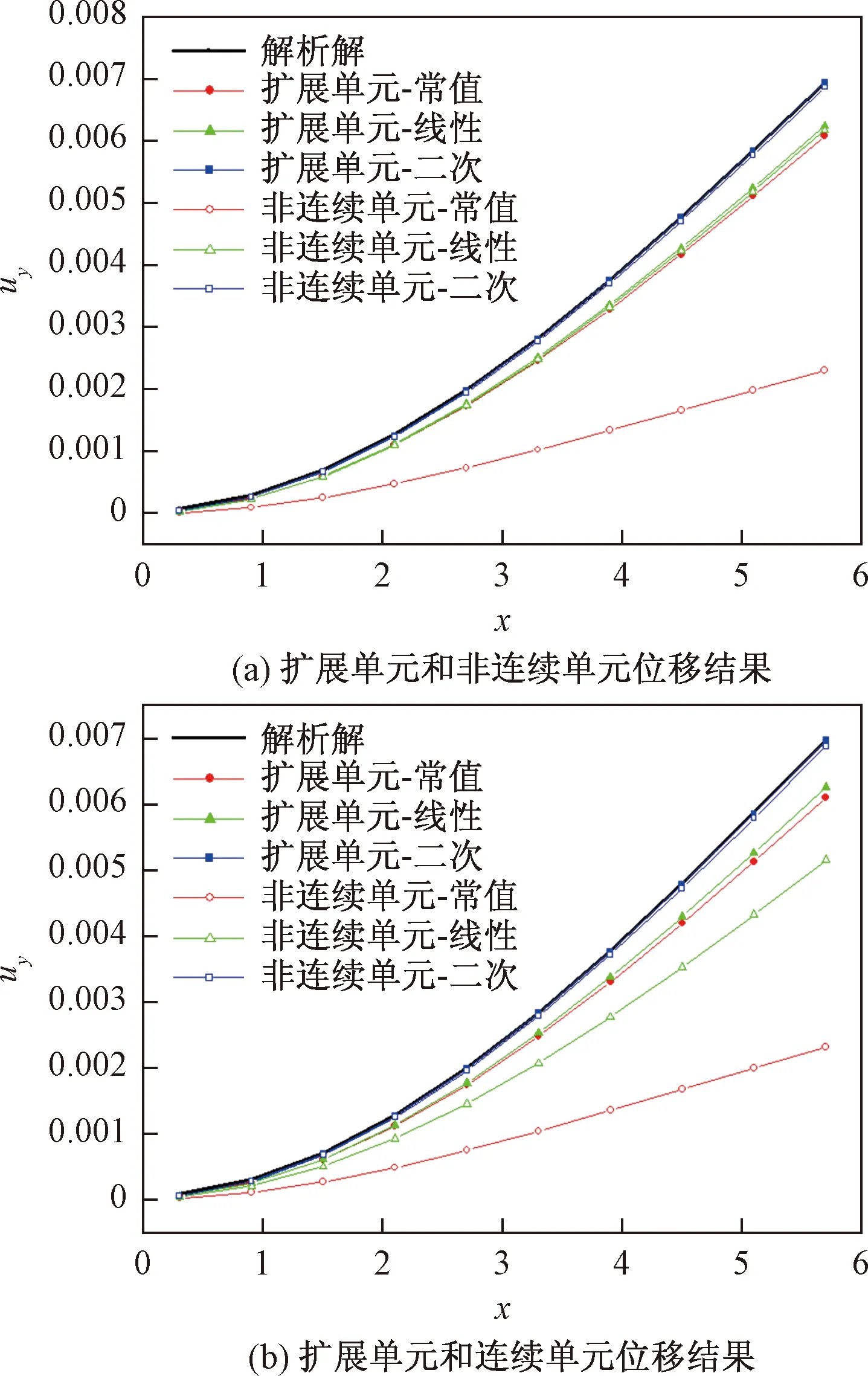
图5 AB边上y方向的位移uyFig.5 The displacement uy along the edge AB

两个小图表示该区域的放大图图6 x=0.5L处正应力Fig.6 The normal stress at x=0.5L

图7 x=0.5L处剪应力Fig.7 The shear stress at x=0.5L
3.2 复杂几何模型
为了进一步验证本文算法,给出了一个较为复杂的计算模型,几何参数如图8所示(其中内孔半径和倒角R1均为1 mm,底边和左侧边的长度分别为8 mm和9 mm),相应的材料参数为:杨氏模量E=1 000.0 MPa,泊松比v=0.25,BC边上遭受均布载荷P=1.0 N的作用。

图8 几何模型Fig.8 The geometry model
在几何模型上共布置260个节点,本文方法计算得到的圆弧AB边上和模型内部EF线上的位移结果如图9、图10所示(把有限元软件采用81 097个节点的计算结果作为参考解)。相应的云图结果如图11~图13所示。

图9 圆弧边AB上的位移Fig.9 The displacement along arc AB

图10 几何模型内部直线EF上的位移Fig.10 The displacement along the line EF in geometry model

图11 x方向位移云图Fig.11 The displacement nephogram in the x direction

图12 y方向位移云图Fig.12 The reference solution of the displacement in the y direction

图13 米塞斯应力云图Fig.13 The reference solution of the Von mises stress
从图9~图13可以看出,采用本文方法得到的圆弧AB边上和内部直线EF上位移的计算结果以及米塞斯应力结果,与用有限元软件得到的参考解吻合得相当好,进一步验证了本文方法的可行性和精确性。
4 结论
采用了一种新型的扩展单元插值方法来求解二维线弹性问题。扩展单元统一了边界元法数值实现中存在的两种类型的单元(即连续单元、非连续单元),既继承了它们的优点,又克服了它们插值过程中存在的缺点。通过在几何角点和边界条件间断处布置两个虚点,无论是连续场还是非连续场,扩展单元插值法都可以精确的估计。另外,由于扩展单元中的虚节点并不被当作源点使用,因此虚节点不会出现在系统方程的系数矩阵中,系统方程系数矩阵自由度的大小并没有发生变化。所以本文方法可以在不增加计算量的前提下,提高了整体的计算精度。数值算例表明,采用扩展单元插值法分析弹性问题时,在保证插值精度的同时,收敛性也得到了提高。
