联合经验正交分解和ARIMA模型的中国地区电离层短期预报

黄良珂，李 琛，王浩宇*，彭 华，陈 军，刘立龙

(1.桂林理工大学测绘地理信息学院，桂林 541004；2.广西空间信息与测绘重点实验室，桂林 541004；3.武汉大学卫星导航定位技术研究中心，武汉 430079；4.武汉大学测绘学院，武汉 430079)

电离层总电子含量是表征电离层延迟的重要参量，提高垂直总电子含量(vertical total electron content，VTEC)预报精度可以提升全球导航卫星系统(global navigation satellite system，GNSS)定位精度；此外，在震前电离层扰动、地球磁场研究、太阳活动对电离层的影响[1-3]等领域亦具有重要意义。常用的VTEC预报模型主要有灰色模型[4]、神经网络模型[5]、Holt-Winters模型[6-7]、ARMA(autoreg ressive moving average)模型[8]和ARIMA(autoregressive integrated moving average)模型[9]等。其中，神经网络模型可以无限逼近复杂的非线性关系，其能较好地用于VTEC的预测，但存在网络优化复杂、参数选取困难和个别预测值误差大等缺点，在一定程度上限制了其实际应用。基于时间序列分析法的总电子含量(total electron content，TEC)预报，已取得丰硕的成果[8-9]。但是直接使用单一的时间序列模型预测TEC，会降低其预测精度。为提高TEC预报精度，文献[10]将小波分解结合ARIMA模型(WARIMA)对TEC进行预报，结果表明：采用WARIMA模型对电离层总电子含量进行预测具有可行性且预报精度优于ARIMA模型。由此可知，对TEC进行预处理可提高TEC预报精度。

经验正交函数(empirical orthogonal function，EOF)分解是一种数理分析方法，可将原矩阵分解成为时间函数和空间函数，根据方差贡献率来简化剔除冗余信息，已广泛应用于具有时空特性和非平稳特性的数据分析中，如降水量分析[11]、平均气温距平值预测[12]和沉降数据的分析[13]等。但目前鲜有文献将EOF函数引入到ARIMA模型对中国地区电离层VTEC进行短期预报研究，尤其在中国低纬度地区。该地区的电离层不仅存在赤道异常现象[14]，也是台风、火山和地震的频发区[15-16]；而台风、火山和地震发生前电离层VTEC会发生异常，高精度的VTEC预报值可以为中国地区(尤其是低纬度地区)地震预报分析[17]和台风对电离层的影响分析[18]提供重要数据源。因此，探讨利用EOF-ARIMA模型对中国地区(2.5°N～55°N，70°E～135°E)的电离层VTEC值进行预测具有重要意义。

1 模型原理简介

1.1 EOF分解和重构基本原理简介

已有文献表明[9-11]，对原始数据进行线性变化，可对原始数据信息进行简化并能剔除其冗余信息，而EOF分解则是一种常用的方法，其可将原始矩阵分解成空间函数矩阵V和时间函数矩阵Y两部分。其中，空间函数部分取决于变量场的主要变化特征，不随时间变化而变化；分解出的时间函数则是由空间点的变量线性组合所构成，为主要分量。具体的过程如下。

(1)设具有时空特性的VTEC为矩阵Xij，空间函数vik和时间函数ykj(k=1,2,…,m)，关系为

(1)

其矩阵表现形式为

(2)

(2)计算方差贡献率，筛选出贡献率超过95%的主分量进行重构，可以有效地剔除原始序列中的多余信息并确保重构后的时空序列可以得到较高精度，方差贡献率可由式(3)得到：

(3)

(3)对符合要求的主分量构成矩阵PC，通过式(4)进行重构。

X=VPC

(4)

1.2 EOF-ARIMA建模过程

假设一个平稳的时间序列为xt(t=1,2,…,N)，则ARMA结构为

xt=φ1xt-1+φ2xt-2+K+φpxt-q+εt+θ1εt-1-θ1εt-1-θ2εt-2-K-θpεt-q+εt

(5)

式(5)中：K为误差；{θ}为白噪声序列；p和q为季节性或非季节性的阶数；φ1,φ2,…，φn为自回归参数。ARIMA模型是对ARMA模型进行差分优化得到，适用于预报非平稳时间序列[19]。

EOF-ARIMA建模步骤如下。

步骤1 数据预处理。研究所使用实验数据为覆盖中国地区的308个格网点2 h分辨率的VTEC值，为此对308个格网点一个季节10 d的原始矩阵为X308×120的数据进行EOF分解，分解出时间函数Y308×120和空间函数V121×120。

步骤2 阶数的确定。对主分量进行季节性分析，以确定ARIMA模型中对季节性预测或非季节性预测的选择，由于选取的电离层总电子含量实验样本具有周期为1 d的周期性变化，因此 季节性预测会获得较高精度；使用序列图分析主分量的周期性，确定是否进行季节性差分D或非季节性差分d；通过自相关图ACF和偏相关图PACF确定非季节性p和q的阶数、季节性P和Q的阶数。

步骤3 预测。根据实验需要确定预测天数，使用相应的阶数对主分量进行季节性预测。

步骤4 重构。把预测后的主分量构成矩阵PC，根据式(6)重构得到5 d的预测值。

2 实验分析

已有文献表明[9]：影响预报精度的因素包括样本数、预报的天数和电离层自身的异常。在控制样本数相同的条件下，结果表明预报前10 d的相对精度最高，超过30 d后预报的精度明显下降；在控制预报天数相同的情况下，当样本数递增至大于30 d后，对预报的精度提升并不明显。因此，结合预报的影响因素和中国地区的实际情况，对国际GNSS服务(international GNSS service,IGS)中心提供的2015年全球VTEC格网数据进行提取，获得覆盖中国地区(2.5°N～55°N，70°E～135°E)的308个格网点2 h分辨率的VTEC数据(图1)。考虑到太阳黑子11 a周期变化[20]，选取4个季节各10 d，共计40 d(年积日分别为春季82～91 d，夏季184～193 d，秋季266～275 d和冬季318～327 d)的VTEC值作为建模数据，采用EOF-ARIMA模型对后5 d的VTEC数据进行预报，并与ARIMA模型进行对比。以IGS中心提供的VTEC值为参考值，采用标准差(STDd)和平均相对精度(Ppd)评估模型预报结果，其表达式为

(6)

(7)

式中：Ipre(t)为预报结果；Iigs(t)为IGS中心提供的VTEC原始序列；由于数据分辨率2 h，因此t代表数据个数，一天的数据个数为12个；STDd表示预报结果与IGS中心提供的VTEC观测值差值的日标准差；Ppd表示预报结果的日平均相对精度。

▲表示选取的中国地区具有代表性的6个网格点图1 中国地区格网点分布Fig.1 Grid mesh distribution in China

3 实验结果分析

3.1 EOF-ARIMA模型预测精度分析

利用EOF-ARIMA模型和ARIMA模型分别对覆盖中国地区的308个格网点4个季节的VTEC进行了预报分析。限于篇幅，只选取了中国地区具有代表性的6个格网点分析预报精度，结果如图2～图7所示。由于IGS提供VTEC时间分辨率为2 h，则每天含有12个VTEC。

由图2～图7可以看出：在所选的6个格网点的4个季节中，EOF-ARIMA模型和ARIMA模型的预测值与IGS中心提供的实测值的变化趋势均具有良好的一致性，但是EOF-ARIMA模型预报的VTEC值与IGS实测值更接近，尤其在(45°N，80°E)格网点处，ARIMA模型表现出较大的预测偏差，说明EOF-ARIMA模型比ARIMA模型表现出更好的预报性能；然而，当样本数据中VTEC值波动较大时，如(35°N,105°E)、(45°N,80°E)和(50°N,130°E)格网点的夏季，两模型的预报精度均有所下降，主要原因可能是ARIMA模型自身的缺陷，面对复杂且规律不明显的时间序列预测其拟合效果较差。尽管如此，经过联合EOF的EOF-ARIMA模型预报性能仍然优于ARIMA模型，在(45°N,80°E)和(50°N,130°E)格网点尤为明显。

图2 5°N,110°E格网点VTECFig.2 Grid point VTEC of 5°N,110°E

图3 25°N,115°E格网点VTECFig.3 Grid point VTEC of 25°N,115°E

图4 30°N,85°E格网点VTECFig.4 Grid point VTEC value of 30°N,85°E

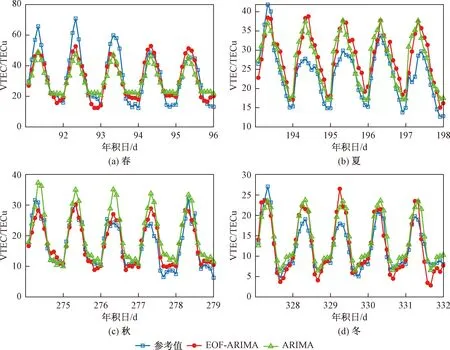
图5 35°N,105°E格网点VTECFig.5 Grid point VTEC of 35°N,105°E

图6 45°N,80°E格网点VTECFig.6 Grid point VTEC of 45°N,80°E

图7 50°N,130°E格网点VTECFig.7 Grid point VTEC of 50°N,130°E

为进一步分析EOF-ARIMA模型在中国地区的预报效果，统计了中国地区308个格网点不同季节的平均日峰值、季节最大日峰值、季节平均标准差、季节平均相对精度，结果如表1所示；此外，对中国地区6个代表性格网点两种模型的预报精度也进行了统计，结果如表2所示。

由于4个季节的季节VTEC平均值存在一定的差异，不宜直接使用标准差进行精度评估。因此，为更好地反映模型的预报精度，采用标准差系数(标准差系数=季节平均标准差/季节VTEC平均值)作为精度指标，标准差系数越高表明预报的精度越低。由表1可知，EOF-ARIMA模型4个季节的平均相对精度均高于80%，在冬季的标准差系数最高，为13.40%；ARIMA模型4个季节的平均相对精度高于70%，在春季的标准差系数最高，为15.77%，其在秋季的预报精度低于其他季节，说明在中国地区的VTEC短期预报中，EOF-ARIMA模型较ARIMA模型具有更高的预报精度和稳定性。由表2可知，在相同季节中，EOF-ARIMA模型的相对精度和标准差均保持在同一预测精度上，比ARIMA模型更稳定，进一步说明EOF-ARIMA模型在中国地区VTEC短期预报中具有更好的稳定性。总之，EOF-ARIMA模型在中国地区预报VTEC的平均相对精度为83.3%，平均标准差为3.51 TECu，在不同的季节中均能保持良好的稳定性，说明在ARIMA模型中引入EOF分解能改善ARIMA模型的VTEC短期预报精度。

表1 两种模型在中国地区的VTEC预报精度统计Table 1 The VTEC prediction accuracy statistics of the two models in China

表2 两种模型在中国地区6个代表性格网点的VTEC预报精度统计Table 2 The VTEC prediction accuracy statistics of the two models in six representative character nodes in China

3.2 不同纬度预报精度分析

电离层赤道异常是由于赤道附近的电离层电子沿着磁力线上升后向高纬度两端移动，在北半球形成驼峰现象，北驼峰主要发生在地磁纬度10°N～12.5°N(地理纬度20°N～22.5°N)[21]。中国地区疆域辽阔，南北方向横跨低、中、高纬度地区，各季节的最大日峰值均出现在低纬度地区且日峰值最大值远大于中国地区的平均日均值。由于在低纬度地区电离层存在赤道异常现象，因此有必要进一步分析EOF-ARIMA模型在中国地区不同纬度的适用性，尤其在中国低纬度地区的适用性。

选取中国地区位于不同纬度的8个格网点[(5°N,110°E)、(15°N,110°E)、(17.5°N,110°E)、(20°N,110°E)、(22.5°N,110°E)、(30°N,110°E)、(40°N,110°E)、(50°N,110°E)]，分析其在不同纬度处预报精度。选取8个格网点夏季的10 d VTEC作为建模数据(图8)，采用EOF-ARIMA模型对年积日184～193 d(夏季)的数据进行后5 d预测，预报结果如表3所示。

图8 中国地区中、低、中高纬度IGS站实测VTECFig.8 Measured VTEC of IGS stations at middle，low and high latitudes in China

由图8可知，在15°N～22.5°N区域VTEC高于其他纬度带，且与纬度不存在相关性，在22.5°N～50°N区域，由于受到太阳辐射较少，VTEC随纬度的升高而降低，说明中国低纬度地区存在电离层赤道异常现象。由表3可以看出，EOF-ARIMA模型在中国地区不同纬度的VTEC预报相对精度均在80%以上，且标准差不存在较大波动，在5°N～22.5°N区域的相对精度达到了84%以上，说明EOF-ARIMA模型的短期预报精度不受电离层赤道异常的影响。总体上，EOF-ARIMA模型在中国地区不同纬度的平均相对精度均高于80 %，说明EOF对数据进行预处理具有剔除冗余信息的作用。通过引入EOF分解可提高ARIMA模型VTEC短期预报能力，使EOF-ARIMA模型在中国地区能取得较高的VTEC短期预报精度。因此，EOF-ARIMA模型在中国地区对VTEC进行短期预报具有较好的适用性和稳定性。

表3 EOF-ARIMA模型在中国地区不同纬度的预报精度统计Table 3 Prediction accuracy statistics of eof-arima model at different latitudes in China

4 结论

基于EOF分解具有对非平稳时间序列进行简化及剔除冗余信息的功能，在ARIMA模型中引入EOF分解，得到组合模型EOF-ARIMA。利用IGS中心提供的覆盖中国地区的2015年2 h分辨率的308个格网点的VTEC数据，分析EOF-ARIMA模型在中国地区对VTEC进行短期预报的适用情况，得出如下结论。

(1)在中国地区，EOF-ARIMA模型的整体预报效果优于ARIMA模型，EOF-ARIMA模型预报5 d的VTEC均方根误差为3.51 TECu，平均相对精度为83.3%，ARIMA模型的标准差为3.67 TECu，平均相对精度为80.0%。

(2)EOF-ARIMA模型的预报性能无明显季节变化，ARIMA模型在秋季的预报精度低于其他季节，说明在ARIMA模型中引入EOF分解可以提升其VTEC短期预报的稳定性和精度。

(3)通过对中国地区低、中、中高纬度格网点的VTEC实测值进行分析，发现在中国低纬度地区VTEC存在赤道异常现象。尽管如此，EOF-ARIMA模型在不同纬度的平均相对预报精度仍然高于80%，且在5°N～22.5°N区域的VTEC预报的相对精度和标准差未出现异常波动，说明EOF-ARIMA模型的短期预报性能不受电离层赤道异常的影响。

基于EOF-ARIMA模型在中国地区及中国低纬度地区赤道异常处进行VTEC短期预报能保持良好的精度和稳定性，为专家学者在该地区进行GNSS导航定位、地震预报分析、火山或者台风对电离层的影响分析以及电离层赤道异常区域分析等其他研究时提供可靠的预测数据进行。