完整井抽降水引起的侧向有界越流承压含水层变形解析研究

蔡兵华，李忠超 ，冯庆高，袁 祥

(1.武汉市市政建设集团有限公司，湖北 武汉 430023；2.中国地质大学(武汉)工程学院，湖北 武汉 430074)

基坑工程中常采用降水井抽取承压水的方式来降低地下水水位以满足施工要求，但抽取承压水不可避免地会引起地层沉降[1-5]。为了避免抽降承压水对周边建筑物或地下构筑物造成的危害，须将基坑降水引起的地层变形控制在合理的范围内。因此，分析抽降承压水引起的地层变形显得尤为重要。

针对基坑降水引起的地层变形问题，许多学者进行了大量研究。如Terzaghi[6]提出土的有效应力原理，解释了降水会引起地层中孔隙水压力的减小致使其有效应力增加，从而导致土层产生压缩变形；Shen等[7]通过结合三维渗流和一维土体固结的方法，提出了关于地下水开采引起地面沉降的计算方法;许烨霜等[8]在考虑了地层压缩性的情况下，分析计算了降水引起的地面沉降问题;Shen等[9]在考虑土体固结过程中压缩系数和渗透系数变化的条件下，建立了三维渗流和一维固结的部分耦合模型，分析了开采地下水对地面沉降的影响。但是更贴合实际的是应考虑地下水渗流和土体变形的相互作用，使渗流和应力实现真正意义上的流固耦合。为此，有不少学者基于Biot固结理论来计算抽水所引起的土体变形。如Derski[10]最早利用Biot固结理论分析了抽水所引起的土体变形问题；Booker等[11]利用Fourier积分变换，求解得到了弹性半空间体内点源稳态抽水作用下土体的Boit固结解析解；艾智勇等[12-13]利用传递矩阵法解决了饱和半空间或饱和成层地基中点源非稳定抽水问题；Selvadurai等[14]应用Laplace-Hankel积分变换求解得到弹性半空间无限体内某一圆盘抽水区域条件下，非稳态抽水引起的土体固结变形的解析解。此外，还有诸多学者[15-19]对此问题进行了研究。

现有的计算研究普遍建立在含水层是侧向无限延伸(侧向无界)假定的基础上，缺少以在距离抽水井r=R(本文将R称为有界半径)处的地下水水位没有变化为边界条件的水位降深解答。而在工程实践中，特别是基坑工程中，往往在距离抽水井r=R处存在补给源(如回灌源)使得该处的地下水水位不发生变化或在r=R处的地下水水位不受抽水的影响，这样的含水系统被认为是侧向有限延伸的，被称为侧向有限含水系统。此外，降水通常是通过竖向抽水井来实现的，应考虑井的完整性这一客观事实。因此，有必要对不同侧向边界条件下完整井抽降承压水引起的含水层变形进行分析。

在抽水过程中通常认为完整井附近的地下水压力和流速仅随含水层的平面方向x、y或r、θ变化，而不随垂直方向z变化，同时还具有轴对称的特点。基于上述完整井抽水的特点，本文在平面应力假定的基础上[20-21]，从Biot固结方程出发，应用Laplace变换求解了越流承压含水层在侧向有界的情况下，完整井抽降水引起的承压含水层竖向变形和径向变形的二维解析表达，并重点分析了不同侧向边界对完整井抽降承压水引起的含水层变形的影响。

1 模型建立及求解

1.1 基本方程

侧向有界抽水承压含水层二维变形计算示意图见图1。侧向有界越流承压含水层中存在一个定流量Q抽水的完整井，抽水承压含水层均质、等厚，含水层内的渗流仅沿径向上发生。其中，抽水承压含水层厚度为B、渗透系数为K、弹性模量为E、泊松比为ν，且抽水承压含水层上覆一个渗透系数为K′、厚度为B′的弱透水层，在距离抽水井r=R处存在补给源使得该处地下水水位没有变化。

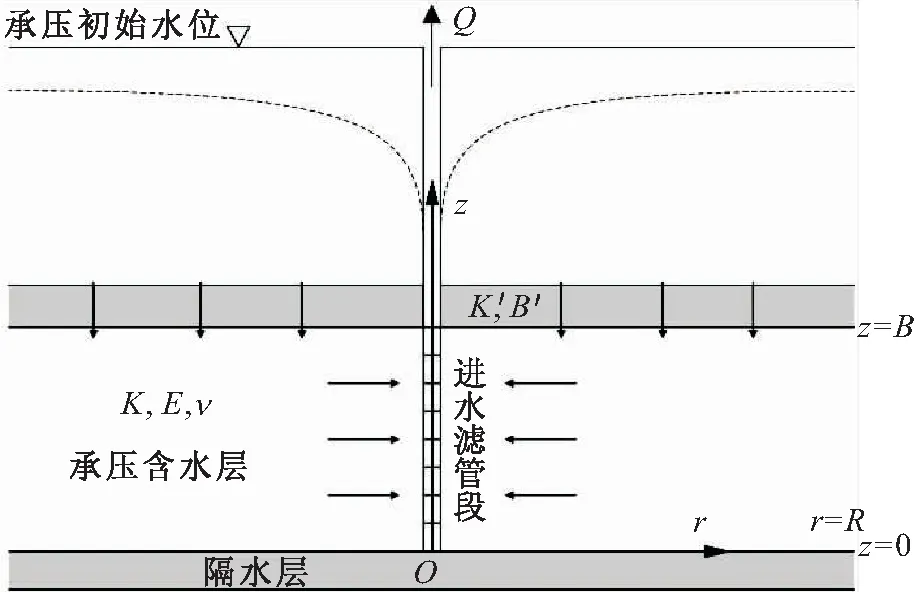
图1 侧向有界抽水承压含水层二维变形计算示意图Fig.1 Schematic diagram of two-dimensional deformation calculation for pumped confined aquifer of laterally finite extent in radial direction

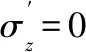
(1)

(2)

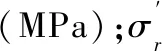
(3)

式中:ur和uz分别为径向位移和竖向位移。

(4)

(5)

再将公式(5)对r积分，可得：

(6)

式中:f称为无量纲积分常数，由通过在距离抽水井r=R处的边界条件来确定。

结合方程(3)～(6)并化简，可得到平面应力状态下土体的基本方程如下：

(7)

(8)

(9)

1.2 固结控制方程的求解

考虑抽水承压含水层上覆土层的越流补给，则土体质量守恒方程为

(10)

式中:K和K′分别为抽水承压含水层和上覆弱透水层的渗透系数(cm/s)；B和B′分别为抽水承压含水层和上覆弱透水层的厚度；γw为水的容重(kg/m3)。

将方程(7)代入方程(10)，可得：

(11)

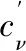
完整井以定流量Q抽水时的井壁边界条件为

(12)

且在r=0处径向变形为零，即：

ur(r→0,t)=0

(13)

同时，在r=R处应满足如下条件：

p(r=R,t)=0

(14)

σrr(r=R,t)=0

(15)

将方程(11)对时间t进行Laplace变换,可得：

(16)

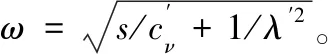
方程(16)的通解为

(17)

式中：I0为第一类0阶修正贝塞尔函数；K0为第二类0阶修正贝塞尔函数。

根据方程(12)和(14)可以确定方程(17)中的待定常数A1和A2，因此可以得到在Laplace空间下，孔隙水压力的解析解为

(18)

随后对方程(7)～(9)进行Laplace变换,并将方程(18)代入，可得：

(19)

(20)

(21)

将公式(20)对r积分，并考虑径向变形满足方程(13)这一条件，可得：

(22)

式中：I1为第一类1阶修正贝塞尔函数；K1为第二类1阶修正贝塞尔函数。

假定抽水承压含水层底部无竖向变形，则含水层顶部竖向变形可表达为

(23)

(24)

在r=R时，由方程(19)、(21)和(22),可得：

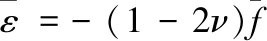
(25)

(26)

(27)

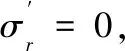
(28)

其中:

(29)

(30)

(31)

(32)

(33)

至此，得到了拉氏空间下的半解析解答，由孔隙水压力和位移的具体表达式(31)～(33)可知，很难对其直接进行拉氏逆变换而得到时间域的解答，为此本文采用常用的Stehfest数值逆变换法[22]来求解实域解。此外，当不考虑越流影响或R→∞时，方程(31)～(33)可以简化为完全承压含水层或侧向无限含水层情况下孔隙水压力和变形的表达式，具体在此不做详述。

2 分析与讨论

本文在上述得到的解析解的基础上，首先通过有限元数值计算的方法对解析解进行对比验证，然后重点分析越流承压含水层侧向有限延伸或无限延伸条件下，完整井抽降承压水引起的含水层竖向变形和径向变形的特征。在无特别说明的情况下，抽水引起的含水层竖向变形和径向变形均表示为正值。

2.1 有限元计算的对比验证

根据上述得到的完整井抽降承压水引起的地层变形的解析解答，将本文计算结果与COMSOL Multiphysics的有限元计算结果进行了对比。依据图1建立了完整井抽降承压水的简化二维有限元计算模型。模型的水平方向尺寸设为1 000 m，由于抽水承压含水层上覆弱透水层的越流补给是通过设置越流项来实现的，故仅需在竖直方向建立厚度为20 m的承压含水层即可；降水井作为线源位于模型中心位置，在线源上即进水滤管处设置流量边界以实现抽水过程，其中抽水流量Q=10 m3/h、抽水时间t=300 h；同时，上覆弱透水层的越流补给量在COMSOL Multiphysics的渗流方程中设置添加越流项即可，其最终考虑越流补给的土体质量平衡方程正如方程(10)一样；此外，模型两侧设置水平方向的位移约束和定水头补给边界，模型底部设置水平和竖直两个方向的位移约束，为不透水边界，并在距离降水井两侧300 m位置处设置定水头边界，以保证抽水过程中该处地下水水位没有变化。整个有限元计算模型共划分为1 146个三角形单元，土体本构模型选用线弹性模型。在有限元计算和解析计算中都采用统一的土体参数值，具体土体参数值见表1。

表1 土体参数值Table 1 Values of soil parameters

表1中的土体参数取值可以如实地反映出含水砂层和黏土弱透水层的基本物理力学特性，以下在对抽水承压含水层变形的影响分析中土层的基本参数取值与表1中一致。本文计算结果与有限元计算结果的对比，见图2。

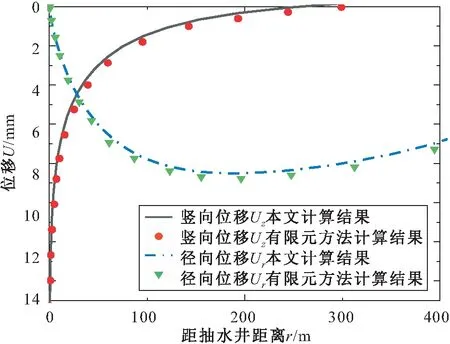
图2 本文计算结果与有限元计算结果的对比Fig.2 Comparison of the calculation results obtained by the proposed solution and the finite element numerical solution

由图2可见，利用本文计算方法得到的完整井抽降承压水引起的含水层竖向位移(Uz)和径向位移(Ur)与有限元方法的计算结果具有较好的一致性，验证了本文计算方法的正确可靠性。

2.2 抽水承压含水层竖向变形的影响分析

在距抽水井距离r=25 m的位置处，侧向无界和有界(有界半径R=300 m)条件下越流承压含水层中竖向位移Uz与抽水时间t的关系曲线，见图3。

图3 侧向无界和有界(R=300 m)条件下越流承压 含水层Uz-t的关系曲线图Fig.3 Relation curves of the vertical deformation (Uz) versus the pumping time (t) in leaky confined aquifer of infinite and finite extent in radial direction (R=300 m)

由图3可见，在整个抽水阶段中，无论承压含水层侧向有界还是无界，其竖向位移Uz都随着抽水时间t的增长而增大，并在后期达到稳定；当抽水时间t小于10 h时，尚未达到渗流稳定阶段，抽水引起的侧向有界和无界含水层的竖向位移基本是一致的，而在抽水后期，侧向有界含水层相对来说更易达到稳定渗流阶段，因此侧向无界含水层的竖向变形要大于侧向有界含水层。

当抽水时间t=300 h时，侧向无界和有界(R=200 m)条件下越流承压含水层的竖向位移Uz与距抽水井距离r的关系曲线，见图4。

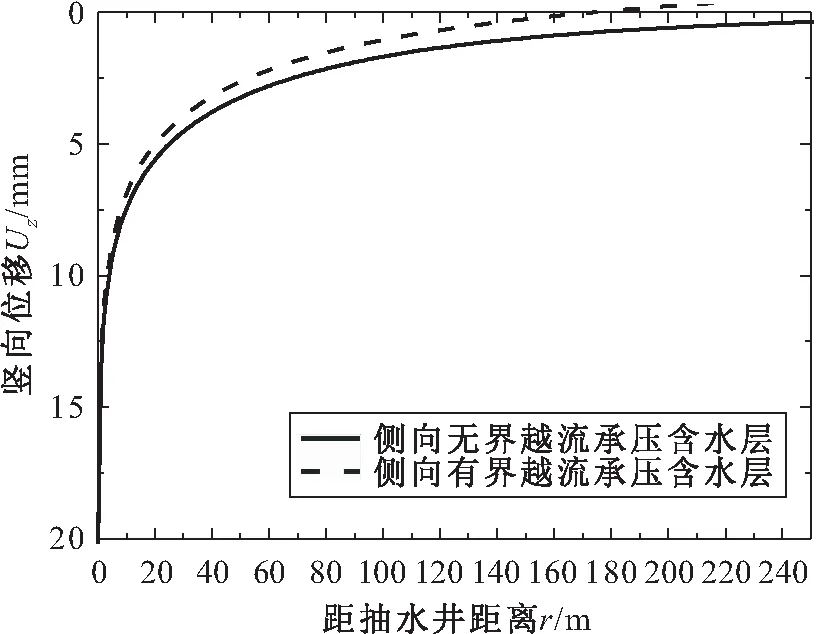
图4 侧向无界和有界(R=200 m)条件下越流承压 含水层中Uz-r的关系曲线图Fig.4 Relation curves of the vertical deformation (Uz) versus the distance (r) in leaky confined aquifer of infinite and finite extent in radial direction (R=200 m)

由图4可见，从含水层土体变形的整体规律上看，无论越流承压含水层是侧向有界还是无界，抽水引起的含水层竖向位移Uz均随着与抽水井距离r的增大而减小；在抽水渗流达到稳定阶段时，侧向无界含水层的竖向变形量要大于侧向有界含水层，且这种变形量的差异在距离抽水井越远的位置越发明显，这是由于越接近侧向边界(R=200 m)，受到侧向边界补给作用的影响更加明显，从而减小了抽水井对竖向变形的影响。

当有界半径R取不同值时，越流承压含水层的竖向位移Uz见图5，为了比较分析，侧向无界含水层中抽水的情况也考虑其中。

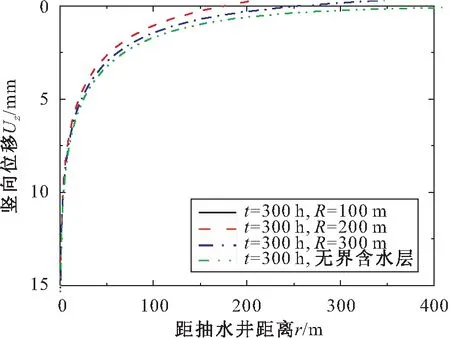
图5 不同有界半径R对越流承压含水层竖向位移 Uz的影响Fig.5 Impact of finite radius (R) on the vertical deformation of leaky confined aquifer

由图5可见，在较长的抽水时间(t=300 h)内，随着有界半径R的增大，侧向有界含水层的竖向位移Uz越接近于侧向无界含水层；在抽水达到稳定渗流阶段后，随着有界半径R的增大，侧向有界含水层的竖向变形范围和具体量值均随之增大，这是由于侧向边界越接近于抽水井，其补给作用对抽水的影响则越明显，从而减小了抽水井所能引起的含水层竖向变形范围和竖向变形量。

2.3 抽水含水层径向变形的影响分析

在距抽水井距离r=25 m位置处，抽水引起的侧向无界和有界(R=200 m)越流承压含水层的径向变形Ur与抽水时间t的关系曲线，见图6。

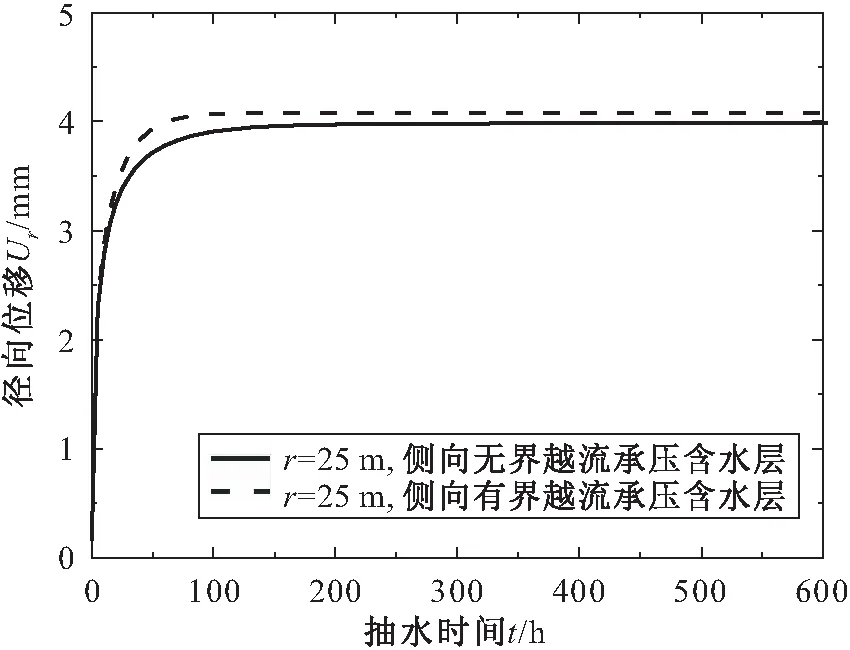
图6 侧向无界和有界(R=200 m)条件下越流承压 含水层Ur-t的关系曲线Fig.6 Relation curves of the vertical deformation (Uz) versus the pumping time (t) in leaky confined aquifer of infinite and finite extent in radial direction (R=200 m)

由图6可见，在整个抽水阶段中，侧向无界和有界越流承压含水层的径向变形Ur均随着抽水时间t的增长而增大，并在达到稳定渗流时保持不变，且此时含水层径向位移达到最大值；此外，在相同的抽水时间，距离抽水井同一位置处侧向无界承压含水层的径向位移要小于侧向有界承压含水层，这是由于在侧向有界承压含水层中，侧向边界位置(有界半径R)处的地下水水位始终保持不变，抽水过程中会形成一个相比于侧向无界承压含水层中更大的水头差和渗流力作用，从而引起含水层更大的径向变形。

在不同抽水时间t=50 h和t=300 h时，侧向无界和有界(R=200 m)条件下越流承压含水层的径向位移Ur与距抽水井距离r的关系曲线，见图7。

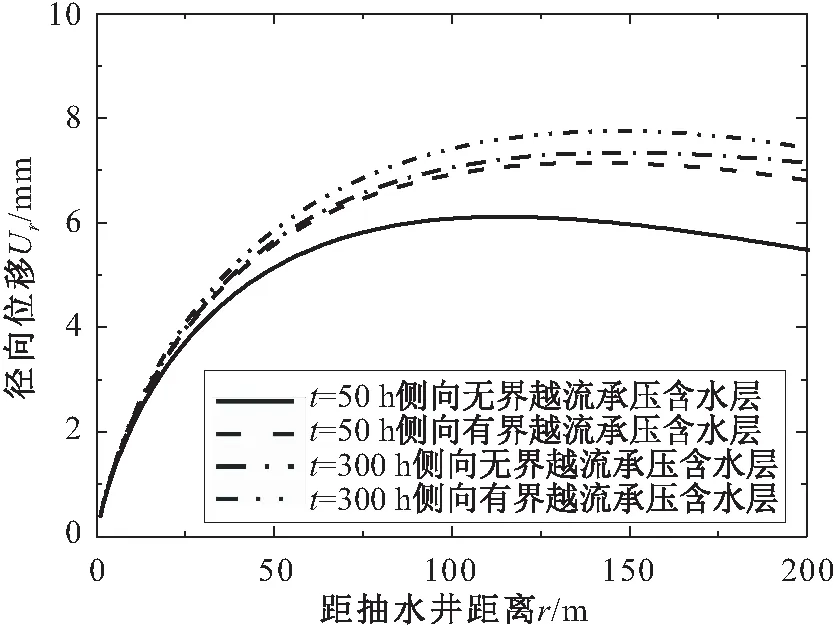
图7 不同抽水时间侧向无界和有界条件下越流承压 含水层Ur-r的关系曲线Fig.7 Relation curves of the radial deformation (Ur) versus the distance (r) in leaky confined aquifer of infinite and finite extent in radial direction under different pumping time

由图7可见，在同一抽水时间，侧向无界和有界承压含水层的径向位移Ur沿径向的分布规律基本一致，即随着距抽水井距离r越远，侧向有界和无界承压含水层径向位移Ur呈现先增大后减小的趋势，这是由于靠近抽水井位置附近的侧向有界和无界承压含水层处于压缩变形区，距离抽水井较远位置的侧向有界和无界承压含水层处于拉张变形区，而侧向有界和无界承压含水层的最大径向变形会出现在这两个区域的交界位置处，因此越流承压含水层的最大径向变形出现在距抽水井一定距离处。

当有界半径R取不同值时，越流承压含水层的径向位移Ur见图8，为了比较分析，侧向无界含水层中抽水的情况也考虑其中。

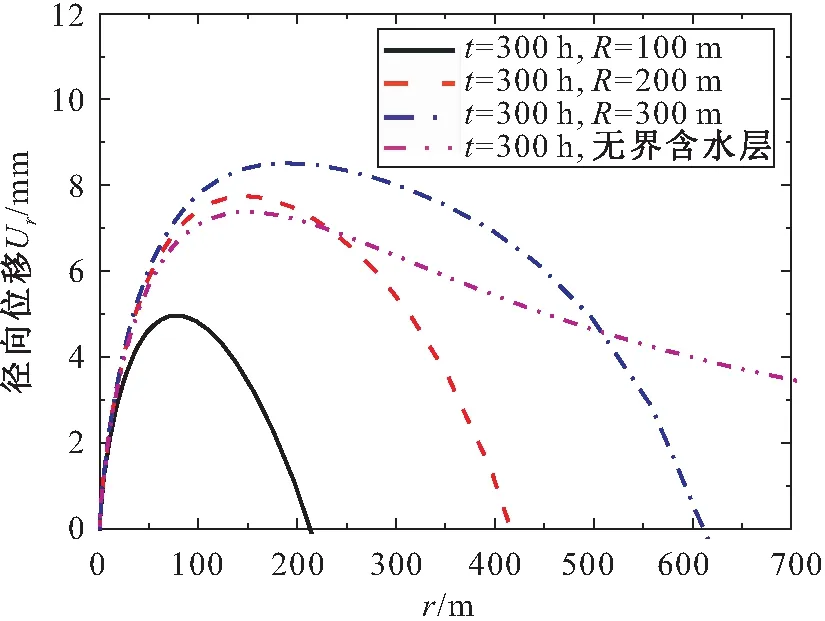
图8 不同有界半径R对越流承压含水层径向位移 Ur的影响Fig.8 Impact of finite radius (R) on the radial deformation of leaky confined aquifer(Ur)

由图8可见，在较长的抽水时间(t=300 h)内，随着有界半径R的增大，抽水井引起的侧向有界承压含水层的径向变形量和变形范围均随之增大，这是由于有界半径R越大，侧向边界对抽水的影响越小，抽水所能引起的含水层径向变形量和变形范围也就越大；同时，随着侧向边界与抽水井相距越远，含水层的拉张变形区也相对距离抽水井越远，进而导致含水层压缩变形区和拉张变形区的交界位置也越远离抽水井，最终呈现如图8所示含水层最大径向变形位置随着有界半径R的增大而远离抽水井这一特征；此外，侧向无界条件下含水层的径向变形规律与侧向有界条件有所差异，这是由于侧向边界的补给作用减小了抽水井对含水层径向变形的影响范围，从而导致侧向无界承压含水层的径向变形范围要大于侧向有界承压含水层。

3 结 论

本文建立并得到了完整井抽降水引起的侧向有界越流承压含水层竖向位移和径向位移的解析解，并重点分析了完整井抽水条件下侧向边界对越流承压含水层竖向变形和径向变形的影响，得到主要结论如下：

(1) 无论抽水承压含水层侧向有界还是无界，在整个抽水阶段，承压含水层的竖向变形在抽水前期均随着抽水时间的增长而增大，并在后期达到稳定保持不变，抽水引起的承压含水层竖向变形也随着距抽水井距离的增大而减小；在达到渗流稳定阶段后，侧向无界承压含水层的竖向变形量要大于侧向有界承压含水层，且这种变形量的差异在距离抽水井越远的位置越发明显。

(2) 在抽水达到稳定渗流阶段时，随着有界半径R的增大，抽水引起的侧向有界承压含水层的竖向变形范围和具体变形量值均随之增大，且其竖向变形的分布规律也越接近于侧向无界承压含水层的情况。

(3) 在整个抽水阶段，侧向无界和有界越流承压含水层的径向变形均随着抽水时间的增长而增大，并在达到稳定渗流时保持不变且承压含水层达到最大径向位移值；在同一抽水时间，随着距抽水井距离的增大，侧向无界和有界承压含水层的径向位移呈现出先增大后减小的变化规律，即越流承压含水层的径向位移的最大值出现在距抽水井一定距离处，且侧向无界承压含水层的径向变形量要小于侧向有界承压含水层。

(4) 在抽水达到稳定渗流时，随着有界半径R的增大，抽水引起的侧向有界承压含水层的径向变形量和变形范围也随之增大，其最大径向变形位置也随之远离抽水井，且抽水引起的侧向无界承压含水层的径向变形范围要大于侧向有界承压含水层。