超导电动悬浮系统基于有限元-解析耦合算法的力特性分析
2020-12-04龚夕霞卢琴芬
龚夕霞,卢琴芬
(浙江大学 电气工程学院,杭州 310027)
0 引 言
磁悬浮列车的车体与轨道无直接接触,相比传统轮轨交通,不存在摩擦阻力,速度能大幅度提升,非常适用于高速交通。目前常用的悬浮方式有电磁悬浮(EMS)与电动悬浮(EDS),EMS是需要控制的主动悬浮,而EDS是不需要控制的被动悬浮,属于自稳定系统。
EDS具有多种结构,悬浮气隙各不相同,其中能实现大气隙悬浮的是超导电动悬浮系统。超导电动悬浮系统中,车载超导磁极产生的强磁场与8字形悬浮线圈的感应磁场相互作用产生悬浮力,该悬浮力随着速度增加而增大,当车辆速度超过一定值后,悬浮力就能与车体重量相平衡,实现车辆悬浮。
超导电动悬浮系统一直是研究的热点,包括结构与计算。前者主要在于采用低成本的高温超导磁极来替代目前高成本的低温超导磁极;后者主要在于优化分析方法。一般的分析方法包括有限元算法、解析算法(如谐波分析法、短时傅里叶变换法、动态电路理论等)。对于EDS系统来说,系统尺寸大,有限元方法虽然精度高,但是计算时间长,不利于进行大量的计算;解析法模型简单,计算方便,但精度不高,因此需要对解析法进行修正改进。
解析过程中,提出互感计算公式、保证互感计算精确度至关重要。文献[1]基于场-路结合的解析方法,计算分析了交叉连接的8字形零磁通线圈与超导线圈组成的悬浮、导向系统。文献[2]采用谐波近似法,忽略了磁通的高次谐波分量,基于场-路-运动耦合模型,得到了正弦规律变化的环路电流。
本文针对超导EDS系统,为解决开放式磁场造成的有限元模型庞大、仿真时间长的问题,提出了一种有限元-解析耦合算法,基于动态电路原理对系统进行了解析建模,再采用有限元法计算模型的电参数,以达到修正解析法的目的,最后基于该方法计算并分析了悬浮系统的性能。
1 系统结构与工作原理
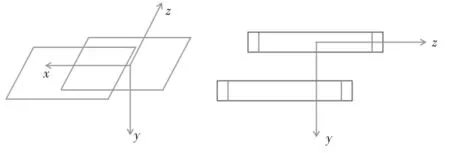
图1显示了超导EDS系统,包括8字形闭合线圈和极性交替变换的车载超导磁极。车载超导磁极提供了实现悬浮所需的强磁场,线圈励磁电流很大,可采用低温超导磁极或高温超导磁极。前者已经应用于日本的MLX01型高速磁悬浮列车,优点是磁场稳定性好;后者是目前的研究热点,因为制冷成本低。无论采用哪种方式,从悬浮力计算的角度来说,其作用都是提供强磁场,并不影响计算模型。

图1 单侧8字形线圈与车载超导磁极模型
超导电动磁悬浮系统具有自稳定特性,悬浮与导向都无需人为控制,图2显示了悬浮与导向的工作原理。

图2 悬浮与导向原理示意图
悬浮原理:当超导磁极跟随着车辆快速前进时, 8字形线圈中匝链的磁场快速变换。根据楞次定律,8字形线圈将会产生感应电流,由于上下两环交叉环绕,因此感应出的电流大小相同、方向相反,产生的磁场方向则相反。下环感应电流所产生的磁场极性与超导线圈一致,而上环相反,两者相互作用便产生了悬浮力。
导向原理:当车体偏离轨道中心线时,由楞次定律知,距离变小的一侧8字形线圈会感应出电流产生斥力,距离变大的一侧8字形线圈感应出电流产生吸引力,最终使得车辆稳定在轨道中心线位置。
2 分析方法
超导EDS系统一般的分析方法为有限元与解析算法,各有优缺点。
2.1 有限元法
有限元法的计算精度较高,基本理念是将一个研究对象分解成多个离散的小单元,对这些小单元进行线性计算,并且通过迭代将单元间的差值控制在合理的范围之内,这样的处理方式有助于解决各类难以计算的微分方程,将解析解转变为数值解。
经分析可知,该磁悬浮结构不适合简化成2D模型进行分析,而3D模型仿真则需要消耗大量的时间。同时,由于该EDS结构中没有铁磁材料,因此磁路将在空气中闭合形成回路,形成开放式磁场。在回路较为分散的情况下,为保证计算精度,需要在建模时将空气部分的范围设置成结构体范围的若干倍,从而造成了模型庞大、仿真时间长、参数调整不方便等问题。
2.2 解析法——动态电路原理
动态电路原理根据一系列与时间、空间相关的电参数,利用一组矩阵形式的微分方程来计算分析电动系统。由于动态电路原理通常用来求解时域中的电流,因此该方法非常适用于磁悬浮列车、电磁发射器等系统的瞬态及动态分析。
2.2.1 无交叉系统
文献[3]介绍了EDS悬浮系统中的动态电路理论应用,提供了合理的数学模型,可用于计算机代码开发。该模型如图3所示,n个8字线圈(2n个线圈环路)作为直线电机的定子,m个超导线圈作为动子。值得一提的是,该模型只取了电动磁悬浮列车的半侧进行建模分析,这是因为磁悬浮列车两侧的竖直悬浮系统相距较远,两侧8字形线圈的相互作用可以忽略不计。

图3 无交叉系统动态电路原理计算模型
计算过程中,需进行如下假设:
(1)超导线圈中的电流保持恒定。
(2)忽略yz平面的运动,即超导线圈只沿着x轴方向运动。
根据动态电路原理,可以得到以下微分方程求解8字线圈中的感应电流。
(1)

根据求解得到的8字线圈感应电流值,可以进一步求解得到系统在x,y,z三个方向上的电磁力。
(2)
(3)
(4)
2.2.2 交叉系统
文献[4]介绍了超导EDS系统两侧8字形悬浮线圈交叉连接后的计算模型,如图4所示。在与无交叉系统相同的假设条件下,基于动态电路原理同样可以得到感应电流与电磁力的计算公式。

图4 交叉系统动态电路原理计算模型

(5)
(6)
(7)
(8)
(9)
(10)
M11(i,j)=M33(i,j)=2mi,j-2mi,n+j
(11)
其中i=1,n;j=1,n;当i=j时,mi,j=L
M22(i,j)=2mi,j
(12)
其中,i=1,n;j=1,n;当i=j时,mi,j=L
M12(i,j)=M21(i,j)=M23(i,j)=
M32(i,j)=mi,n+j-mi,j
(13)
其中,i=1,n;j=1,n;当i=j时,mi,j=L
(14)
(15)
(16)
ib j=ic j(i=1,n)
(17)
ib n+1=ic n+j-ic j(j=1,n)
(18)
ib 2n+j=ic 2n+j-ic n+j(j=1,n)
(19)
ib 3n+j=-ic 2n+j(j=1,n)
(20)

(21)
(22)
(23)
3 电感计算
由以上公式可以看到,基于动态电路原理的方法进行求解时需要进行大量的电感、电感关于坐标轴导数的计算,显然计算结果的正确性很大程度上取决于电感的准确性。电感的计算可采用有限元方法以及解析算法。
3.1 有限元计算
采用有限元软件JMAG可以对线圈电感进行仿真计算,且无需对线圈形状进行简化,计算精度相对较高。不过有限元只能得到数值解,无法获悉解析解,求解互感关于坐标轴的导数值较为复杂,一般采用拟合的方式得到互感解析式,再进行相应的求导计算。
经Matlab中Cftool工具拟合发现,该互感可以用式(24)表示。
(24)
式中,pi(i=1,2,3,4,5),qi(i=1,2,3,4) 为未知数,x为8字线圈中心点与超导线圈中心点在x轴方向上的距离,拟合效果如图5所示。

图5 8字形线圈单环与超导线圈互感拟合效果图
3.2 解析算法
解析算法中,为便于计算,需要对模型的形状进行简化,如图4所示,将两端呈圆弧状的超导磁极长环简化成一个矩形(根据文献[5]中面积不变的原则确定等效后的长度),于是计算所需的互感就转变为各个矩形线圈间的互感值。
3.2.1 矩形截面的矩形线圈的电感[6]
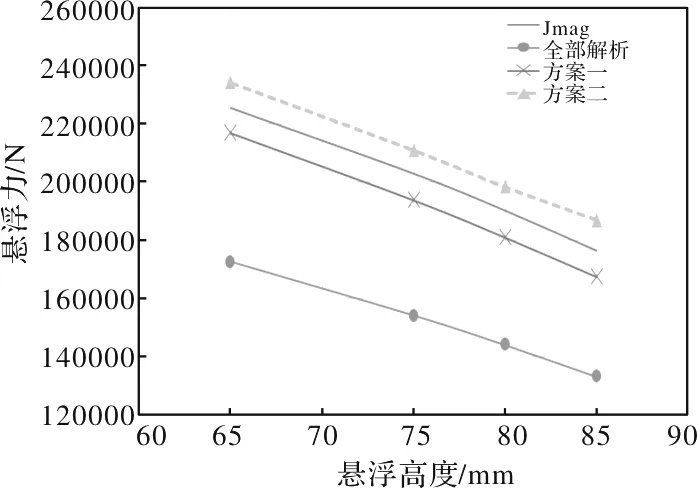
若矩形线圈的匝数为ω,截面尺寸为a×r,中心线匝的尺寸为b×c(b 图6 8字线圈单环图 (25) 就正方形线圈而言 ,则公式变为 (26) 3.2.2 同一平面两个相距较远的矩形回路的互感 当线圈相距较远,间距为线圈尺寸的3倍及以上时,可采用泰勒级数法求解互感[6] (27) 式中,u=cosθ,v=sinθ,Sk、Si为两个矩形的面积;r为矩形中心点的距离;θ为两个矩形中心连线与平面水平线的夹角。 3.2.3 两个各边相互平行的矩形线圈的互感[7] 如图7所示,当两个矩形线圈的对应边相互平行,并且与矩形线圈总体尺寸相比,其截面尺寸能忽略时,可利用聂以曼公式求解线圈互感。 图7 8字线圈与超导线圈模型 (28) (29) 基于以上分析,结合有限元与解析法,本文提出了一种有限元-解析耦合算法,其利用动态电路原理建立计算模型,借助有限元软件计算模型中的电感参数,便于提高模型参数的准确性以及计算精度。 以无交叉系统为例,耦合算法可分为两种方案,方案一中一半电感来自于有限元结果,方案二中全部电感都来自于有限元结果: (1)方案一:L与mi,j采用有限元计算。 (2)方案二:L、mi,j及Mi,j、Gi,j都采用有限元计算。 图8显示了一个超导EDS系统的示意图,包括8字形线圈与车载超导线圈,具体模型参数如表1所示。 图8 8字形线圈与车载超导线圈模型尺寸示意图 表1 模型参数表 基于前述的有限元分析法、解析法与二种耦合算法,可以计算出系统的悬浮力特性。图9显示了75 mm悬浮高度、500 km/h速度下的计算结果。由于有限元模型更接近实际模型,结果将更准确,因此以JMAG有限元仿真结果作为标准,得到各方法与有限元仿真结果的误差大小,如表2所示。 表2 悬浮力误差对比 图9 悬浮力随悬浮高度的结果对比 解析法的误差比较大,是因为计算过程中所用的互感公式带有误差,如部分公式中忽略了线圈的厚度;而且图形的简化使得计算模型与实际模型具有一定的差异,如将超导线圈简化成了矩形、将8字形线圈单环的边长简化成了最外侧与最内侧边长的平均值。 尽管基于JMAG的有限元分析结果最为准确,但是当模型较大时,需要消耗漫长的仿真时间,效率不高;完全采用解析法进行计算快速且方便,但具有较大的误差;耦合方案一通过有限元计算得到了定子部分的自感、互感,而8字线圈与超导线圈的互感采用解析法进行分析,虽然方案一在解析法的基础上增加了有限元仿真的工作量,但增大了计算的精度,在定子结构不变的情况下,只需要进行一次有限元仿真即可;耦合方案二中的电感参数都来自于有限元模型,计算量增多,但结果误差跟方法一相差不大。因此耦合方案一比较合适,以下采用该方法对悬浮系统的动态特性进行分析。 当车辆速度增加时,电动磁悬浮列车的悬浮力不断增大,直至悬浮力与列车自身重量相等时,列车达到稳定悬浮状态(交叉与非交叉系统在轨道中心线位置,即无导向偏差时,悬浮力大小相差无几)。图10为采用耦合方案一得到的悬浮高度与速度的特性曲线。由图10可见,车辆提速到一定程度之后,其稳定悬浮的高度基本不变,意味着在该结构下,磁悬浮列车加速的过程中具有一定的悬浮稳定性,尤其是在高速阶段,其悬浮气隙基本保持恒定,因此该悬浮方式可适用于高速与超高速的运行状态。 图10 悬浮高度与运行速度的关系曲线 在运行过程中,列车的导向出现偏差时,车辆将偏离轨道中心线,并造成车辆与两侧8字形悬浮线圈距离不等的现象。此时线圈之间的互感发生变化,线圈电流、列车悬浮力改变,距离减小的一侧产生的悬浮力增大,距离增大的一侧反之,由于增大程度高于减小的程度,因此偏移后两侧悬浮合力增加、稳定悬浮高度增大。图11为无交叉系统不同速度、不同导向偏移时的稳定悬浮高度,符合上述规律,并且可以看出,在高速情况下,稳定悬浮高度相差不大。 图11 无交叉系统中速度、导向偏差对悬浮高度的影响 另外,据文献可知,两侧8字线圈交叉连接的方式,相比无交叉系统具有更好的悬浮刚度[1],因此针对两种连接方式进行了比较分析。图12为交叉与无交叉系统在不同导向偏差时的悬浮高度,图13为交叉与无交叉系统不同导向偏差时两侧悬浮力的差值大小。显然,当偏移的距离增大时,两侧的悬浮合力增幅越来越大,导致了稳定悬浮高度逐步提升,但交叉系统悬浮高度的增幅较小,且左右侧悬浮力差值较小,相比之下更加稳定。 图12 不同导向偏差对悬浮高度的影响 图13 不同导向偏差对两侧悬浮力差值的影响 悬浮系统产生悬浮力的同时,也会产生制动力。由图14可知,交叉系统在低速状态下的制动阻力更大,若采用交叉连接方式,则需要更大的驱动力。同时,相比低速的运行情况,高速前进时车辆的制动力较小,因此该悬浮方式可应用于高速和超高速的运行模式。 图14 不同速度情况下悬浮线圈的制动力 本文针对超导电动磁悬浮系统,提出了有限元-解析耦合算法,方案一通过有限元计算解析模型中的部分电感,方案二通过有限元计算了全部电感。结果表明,两种方案都能够把计算误差从约24%降低到6%以下,悬浮高度越小时误差越小,但前者计算速度更快速。基于该耦合模型,快速计算了不同运行速度、不同悬浮高度与不同导向偏差时的悬浮高度,以及不同速度下的制动力。 该方法解决了有限元仿真模型仿真时间长、不易进行参数化分析等问题,能够实现准确且快速的计算,实现模型的优化设计与性能分析。另外,该方法还可运用于超导磁悬浮列车的牵引系统中,完成牵引线圈与超导磁极之间相互作用力的计算。
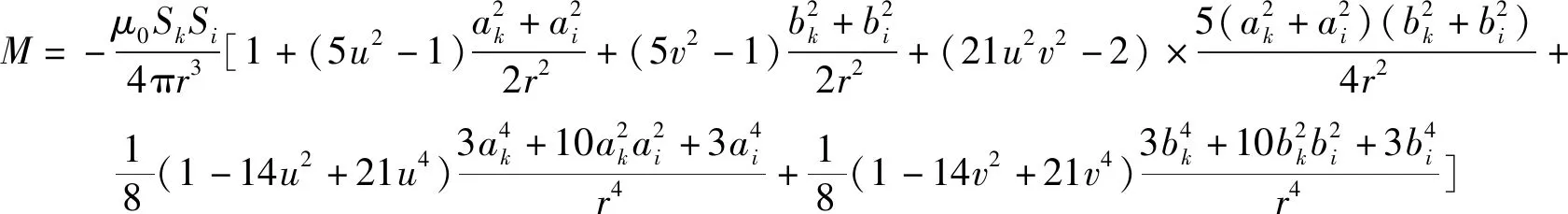
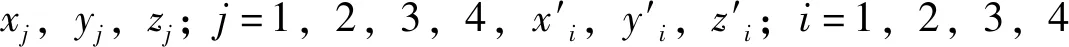
4 耦合算法及验证
4.1 耦合算法
4.2 算法验证



5 动态特性
5.1 悬浮高度与速度的关系

5.2 导向偏差对悬浮高度的影响



5.3 运行阻力

6 结 论
