缺相故障下永磁同步电机电磁径向力动态特性分析

韩海风，邓明星 ，张海军 ，马 强 ，向立明 ，陈 远

(1.武汉科技大学 汽车与交通工程学院, 武汉 430081；2.湖北文理学院 纯电动汽车动力系统设计与测试湖北省重点实验室,湖北 襄阳 441053)

0 引 言

众所周知，交流永磁同步电机具有结构简单、体积小、重量轻、高功率密度、高效率、响应快、调速范围宽等优点，使得永磁同步电机近些年在各个领域的应用越来越广泛[1-2]。

目前振动和噪声已经成为衡量永磁同步电机性能的主要技术指标之一[3-4]。电动机的振动噪声主要源于三个方面：首先是电磁噪声，在电磁力作用下，定转子会产生一定的变形和振动，便产生电磁噪声[5]；接着是机械噪声，当轴承、转子不平衡等情况出现时，便引起机械噪声；最后是空气动力学噪声，主要由空气流动产生[6-7]。现在电磁径向力已经被确定为噪声和振动的根本原因[8]。

对于电机电磁特性的分析研究，传统方法很多都基于有限元针对静态的电磁特性进行分析研究。文献[9]提出了一种减振的优化设计方法，建立了电磁力的有限元模型，利用该模型进行模态计算，得到了低阶固有频率；文献[10]使用解析法来计算电机的磁场和电磁力，采用有限元方法对电机定子进行了振动仿真，分析了电磁激振力与振型之间的关系；文献[11]研究了气隙变形对内永磁同步电动机电磁性能和径向振动特性的影响，分析电磁有限元模型中不同的气隙状态，比较了定子椭圆变形、转子离心变形对气隙磁场、径向磁力和切向磁力以及电磁转矩的影响；文献[12]研究了极槽组合对永磁同步电机噪声和振动的影响。利用电磁有限元分析和等效磁化电流法计算电机的局部力，并利用有限元分析方法对局部力引起的振动进行了分析比较；文献[13]建立了永磁直流换向器电磁振动和噪声预测的数值模型，将有限元法和边界元法相结合，分析研究电机的电磁、机械和声学特性，采用有限元方法，在二维气隙区域内计算了作为电机电磁振动和噪声源的电磁场。

本论文针对电动汽车用永磁同步电机，考虑不同负载下电磁径向力动态特性及其在缺相故障状态下的不同响应特性进行理论与仿真分析。首先对电机磁通密度进行推导，接着推导电感与d轴、q轴气隙磁导的关系，最后构建出径向电磁力数学模型。然后基于MATLAB软件建立三相永磁同步电机缺相故障下的电磁径向力仿真模型，最后通过仿真对永磁同步电机的缺相故障下电磁径向力动态特性进行分析。

1 三相永磁同步电机数学模型

1.1 自然坐标系下数学模型

(1)电压方程

(1)

式中,ψ3s为三相绕组的磁链；u3s、R、i3s分别为三相绕组的相电压、电阻和电流。其中，

i3s=[iAiBiC]T；R3s=diag[RRR]；

ψ3s=[ψAψBψC]T；u3s=[uAuBuC]T。

(2)磁链方程

ψ3s=L3si3s+ψf·F3s(θe)

(2)

式中,L3s为三相绕组的电感；F3s(θe)为三相绕组的磁链。其中，

F3s(θe)=[sinθesin(θe-2π/3) sin(θe+2π/3)]T

其中，Lm3为定子互感；Ll3为定子漏感。

(3)转矩方程

(3)

式中,pn为电机的极对数。

(4)运动方程

(4)

式中,J为转动惯量；ωm为电机的机械角速度；TL为负载转矩；B为阻尼系数。

1.2 坐标变换

三相永磁同步电机的坐标变换包括静止坐标变换和旋转坐标变换，其关系如图所示，ABC为自然坐标系，α-β为静止坐标系，d-q为同步旋转坐标系。

图1 三相永磁同步电机坐标系关系

(1)自然坐标系变换到静止坐标系

[fαfβf0]T=T3s/2s[fAfBfC]T

(5)

式中,f为电机的电压、电流及磁链等变量；坐标变换矩阵为

(6)

(2)静止坐标系变换到自然坐标系

[fAfBfC]T=T2s/3s[fαfβf0]T

(7)

其中，坐标变换矩阵为

(8)

(3)静止坐标系变换到同步旋转坐标系

[fdfq]T=T2s/2r[fαfβ]T

(9)

其中,坐标变换矩阵为

(10)

(4)同步旋转坐标系变换到静止坐标系

[fαfβ]T=T2r/2s[fdfq]T

(11)

其中,坐标变换矩阵为

(12)

(5)自然坐标系变换到同步旋转坐标系

[fdfqf0]T=T3s/2r[fAfBfC]T

(13)

其中,坐标变换矩阵为

(14)

(6)同步旋转坐标系变换到自然坐标系

[fAfBfC]T=T2r/3s[fdfqf0]T

(15)

其中,坐标变换矩阵为

(16)

2 径向电磁力的动态数学模型

2.1 关于径向电磁力的假设

(1)由d轴电流、q轴电流和永磁体产生的磁通量分布是线性无关的。

(2)d轴电流和q轴电流产生的磁通密度均匀分布在齿面上。

(3)周向磁通密度为零。

在这里，d轴电流和q轴电流与传统电机矢量控制中使用的电流相同，通过相对变换得到[15]。

2.2 磁通密度的推导

根据上述假设(1)，磁通密度Br(t)是由永磁体BM(t)、d轴电流Bd(t)、q轴电流Bq(t)产生的线性无关的磁通密度之和:

Br(t)=BM(t)+Bd(t)+Bq(t)

(17)

永磁体产生的磁通密度：

(18)

式中,Ke为感应电压常数；k2为比例系数；ω为角频率；θ为转子位置角。

d轴电流和q轴电流分别产生的磁通密度

(19)

(20)

式中，k1为比例系数，Ld为d轴电感，Lq为q轴电感，Id1为d轴电流峰值，Iq1为q轴电流峰值。

2.3 电感与d轴、q轴气隙磁导的关系

(21)

(22)

式中,m为定子相数，N为各相定子绕组匝数，P为极对数；基波绕组因数Kw=Kp·Kd，λd、λq分别为d轴、q轴气隙磁导。

本文研究对象电机转子永磁体尺寸如图所示，转子直径为D，永磁体轴长l,d轴磁化方向宽度为a，q轴磁化方向宽度为c，磁化方向长度为b，转子中心到永磁体垂直距离为n。

图2 三相永磁同步电机转子永磁体布置

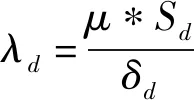
(23)

式中,λd为d轴气隙磁导，Sd为d轴方向永磁体与定子内圆相对面积，δd为d轴方向气隙长度，

(24)

式中,λq为q轴气隙磁导，Sq为q轴方向永磁体与定子内圆相对面积，δq为q轴方向气隙长度。

2.4 径向电磁力的推导

径向电磁力表示如下：

(25)

式中,μ0为磁导率；Br为径向磁通密度；Bθ为周向磁通密度。

通过将电机定子每齿的机械角度 转换成电角度得到积分区间为150°，则径向电磁力：

(26)

根据假设(3), 周向磁通密度为零设置为0,则：

(27)

其中,

(28)

电机磁铁的电磁力：

(29)

d轴电流导出的电磁力：

(30)

(31)

q轴电流导出的电磁力：

(32)

(33)

(34)

3 缺相故障下电磁径向力建模

基于Matlab/Simulink软件平台搭建三相永磁同步电机缺相故障下电磁径向力仿真模型，首先通过第二节电磁径向力的计算编写电磁径向力的计算编程，接着调用M函数将编程写入其中，最后接入搭建的三相永磁同步电机缺相故障下的仿真模型。通过实时的d轴、q轴电流和时间输入，得出电磁径向力的动态特性仿真图，以此来观察和分析三相永磁同步电机缺相状态下的电磁径向力的动态特性。

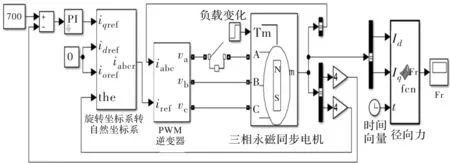
图3 三相永磁同步电机缺相电磁径向力仿真模型

4 电磁径向力动态仿真结果分析

4.1 电机正常运行时

由式(25)到式(34)可知，电磁径向力是随电流和时间变化的函数，从图4可以看出，当三相永磁同步电机定子三相绕组均正常运行、内转子正常转动且负载保持不变时，电机定子齿与转子内嵌式四对磁极永磁体之间的电磁径向力波形呈现规律周期且平稳变化，近似正弦交变。

图4 电磁径向力

4.2 负载变化时

从图5可以看出，当三相永磁同步电机定子三相绕组均正常运行，负载在0.04s由低向高增大时，电磁径向力波形仍然保持正弦，幅值范围由3.15×1012Nm到1.07×1013Nm增至4×1011Nm到1.38×1013Nm，但是其抖振明显增加；当三相永磁同步电机定子三相绕组均正常运行，负载在0.04s由高向低减小时，电磁径向力波形仍然保持正弦，幅值范围由7×1011Nm到1.33×1013Nm降至3.12×1012Nm到1.07×1013Nm，但是其抖振明显降低。

图5 电磁径向力

4.3 缺A相故障时

从图6可以看出，当三相永磁同步电机较低负载保持不变，定子三相绕组A相在0.083s断开时，电磁径向力变化为近似正弦变化，幅值由3.13×1012Nm到1.07×1013Nm增至-1.01×1014Nm到1.15×1014Nm，其抖振尤为剧烈并呈现一定规律；当三相永磁同步电机较高负载保持不变，定子三相绕组A相在0.083s断开时，电磁径向力变化为近似正弦变化，幅值由4×1011Nm到1.4×1013Nm增至-2.25×1014Nm到2.4×1014Nm，其抖振更加剧烈并呈现一定规律。

图6 电磁径向力

5 结 论

本文通过对三相永磁同步电机电磁径向力动态特性分析研究，发现:

(1)定子三相绕组均正常运行、内转子正常转动且负载保持不变时，电磁径向力波形呈现规律周期且平稳变化，近似正弦交变。

(2)定子三相绕组均正常运行，但负载由低向高增大时，电磁径向力幅值范围随之增大，反之则相反。

(3)定子三相绕组缺A相故障下，电磁径向力幅值范围增大数十倍以上。

以上结论以及对电机的电磁径向力动态特性的理论与仿真分析可以为三相永磁同步电机振动分析与控制以及电机振动噪声控制提供理论参考，特别为三相永磁同步电机缺相故障下电磁径向力控制以及电机振动噪声控制提供理论参考。