基于摩擦因数的螺旋密封性能影响因素分析

黎义斌，李建忠，白小榜

(1. 兰州理工大学能源与动力工程学院，甘肃 兰州 730050； 2. 重庆水泵厂有限责任公司，重庆 400033)

螺旋密封是1种非接触式流体动密封，其最显著的特点在于即便密封转子与定子之间存在间隙，也能够起到良好的密封作用.比起其他形式的密封，螺旋密封的安装和维修更为简便，因此得到广泛运用.

国外学者从不同的角度研究了螺旋密封，工程上普遍运用CREASE[1]基于“流量平衡”建立的封液能力求解公式.CHILDS等[2]通过试验研究了不同雷诺数下螺旋角对密封泄漏量和摩擦因数的影响.MCGREW等[3]通过理论和试验的方法对螺旋密封内部的层流和湍流流动进行了研究，分析了影响螺旋密封性能的因素.RICHARD等[4]通过数值模拟研究了螺旋槽上游泵送机械密封槽型对泄漏率的影响.SHAHIN等[5]通过数值模拟研究并分析了螺旋槽和楔形槽的干气密封气膜流场.张彩云等[6]通过对螺旋密封内泵送速度分布规律和沿环形缝隙的泄漏流量进行修正，重新建立了封液能力求解公式.杨晓宗[7]通过引入黏度因子并考虑转子偏心率对螺旋密封性能的影响，对封液能力求解公式进行了修正.刘忠伟等[8]利用Matlab对密封系数进行了优化.宋鹏云等[9]以开漏比作为性能指标，研究了锯齿形螺旋槽干气密封的性能.薄相峰等[10]采用试验方法研究了参数对螺旋密封性能的影响.陈果等[11]以幂律流体为研究对象，研究了介质为非牛顿流体的螺旋槽上游泵送机械密封性能.ZHANG等[12]研究了不同螺旋角下螺旋密封的泄漏特性和动力学特性.

目前，国内外关于螺旋密封的相关研究较多，但在离心泵用螺旋密封的机理方面的研究不系统，工程应用仍然面临很大的不确定性.文中基于CFD数值模拟，从摩擦因数的角度研究螺旋角、相对槽宽和相对槽深对螺旋密封性能的影响，为螺旋密封的研究与应用提供理论依据.

1 计算模型与网格

1.1 三维模型

螺旋密封结构如图1所示，基本参数bg为螺纹槽宽，mm；bL为螺纹齿宽，mm；h为螺纹槽深，mm；c为密封间隙，mm；α为螺旋角，(°)；D为密封直径，mm；L为密封长度，mm；i为螺纹头数；r=bg/(bg+bL)为相对槽宽，量纲一；H=(h+c)/c为相对槽深，量纲一.三维模型如图2所示.为了能获得准确的模拟结果，参照文献[13]所采用的流域划分方法，将流域分为动区域和静区域2部分.

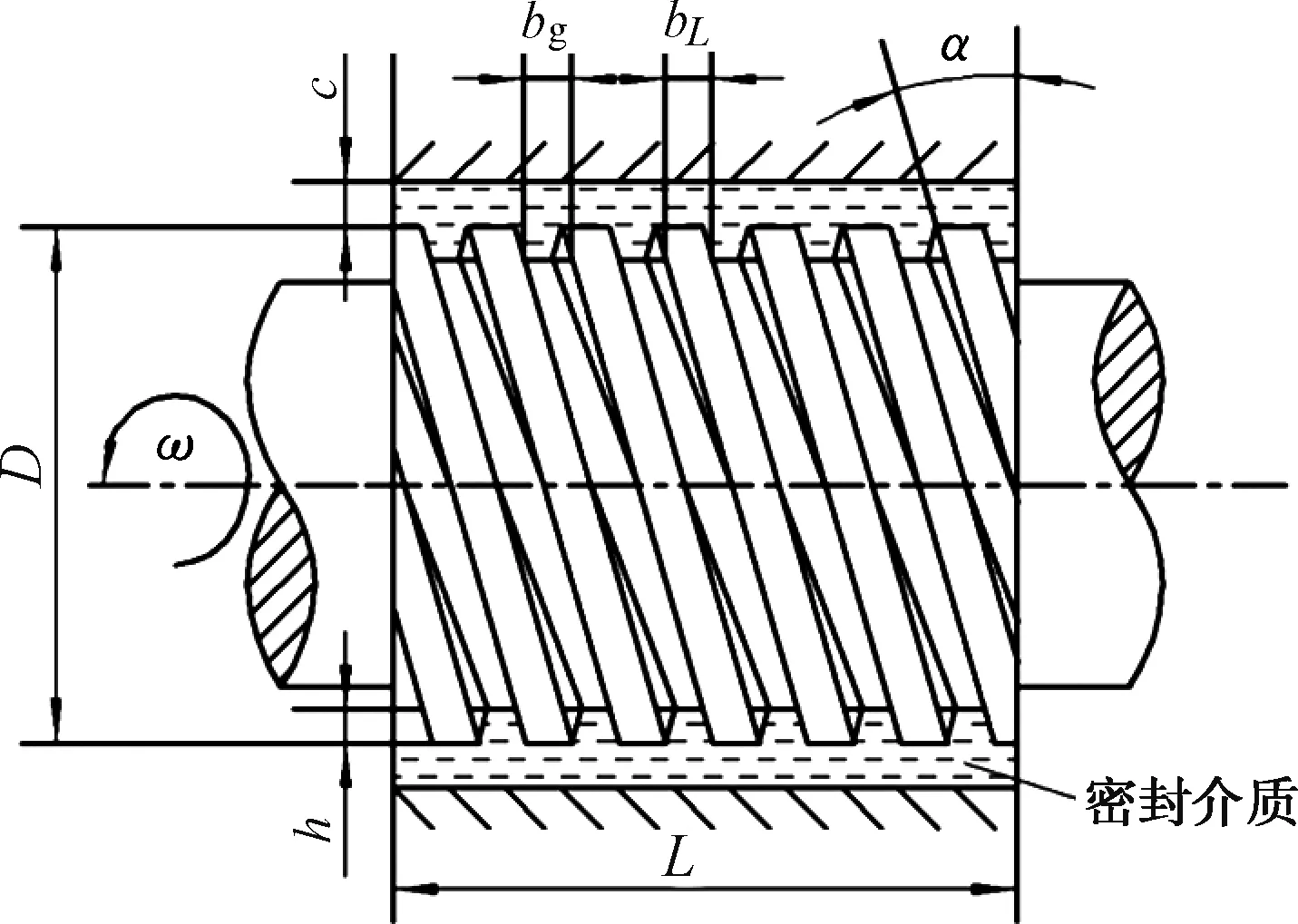
图1 螺旋密封结构简图

图2 螺旋密封三维模型

封液能力求解公式[1]为

(1)

其中

(2)

式中：Cs为螺旋密封几何形状系数，通过Matlab对Cs进行优化，可得出r=0.5,H=3,α=21.05°时Cs取得最大值0.577.在此基础上控制其他影响因素不变，对不同螺旋角、相对槽宽和相对槽深的螺旋密封进行定常数值模拟，具体研究参数如表1所示.

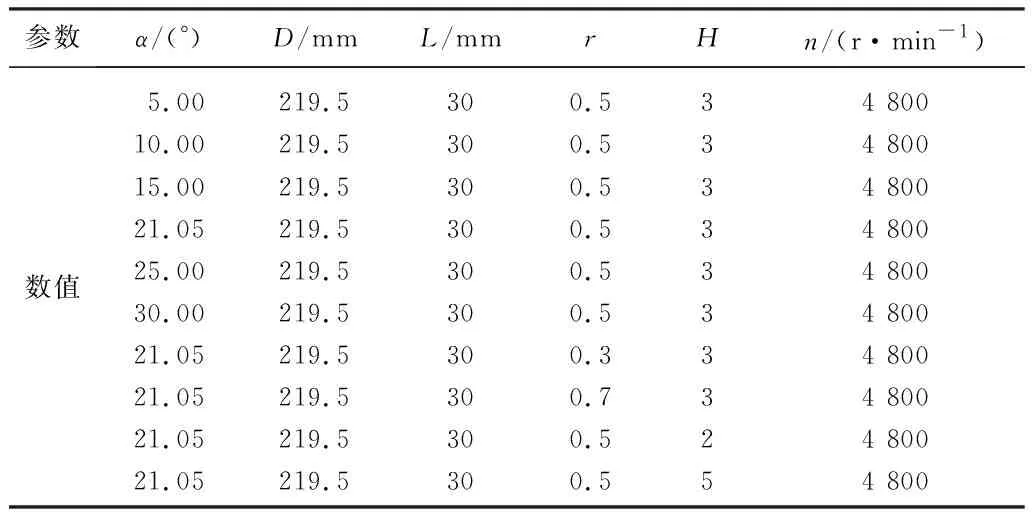
表1 螺旋密封研究参数

1.2 网格划分

采用ICEM CFD对计算域进行六面体网格划分，静止区域及进、出口延长段结构简单，网格划分难度小，螺旋槽道区域结构复杂，网格划分难度大，需要先对1条螺旋槽道创建Block，定义网格参数和周期性，然后将几何与Block进行周期复制，生成完整区域网格，将各部分网格合并得到完整计算域网格，如图3所示.

因壁面剪切作用对流动影响较大，需对近壁面处网格进行加密，以便能准确地捕捉壁面剪切应力和压力分布.

近壁面处剪切方程为

(3)

其中U*为量纲一数，

(4)

网格节点到壁面的距离量纲一化为

(5)

式中：Cμ为湍流黏度系数，其值为0.09；κ为von Kármán系数，其值为0.4187；E为经验系数；UP为近壁面处点的平均流速；κP为点P的湍动能；yP为点P到壁面的距离；μ为流体动力黏度.y*表达式准确度要高于y+，能更准确地表达边界层厚度.文中所划分的网格保证壁面y*在10以下.

图3 螺旋密封计算域网格

网格独立性研究用于验证网格数量对压力计算的影响，图4为螺旋密封进口压力pin随网格数量N的变化曲线，网格数量由105增加到106时，进口压力减小0.006 4%.为确保模拟准确性，减少计算时间，文中控制网格数量在2 500 000左右.

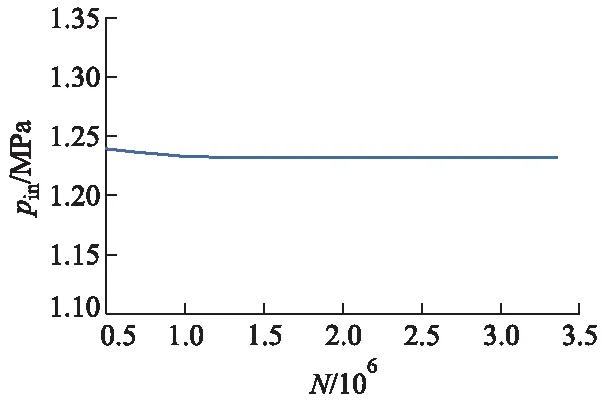
图4 螺旋密封网格无关性验证

2 数值计算方法

2.1 湍流模型

假设螺旋密封内部流动为三维、定常、黏性、不可压流动，介质的动力黏度为常数.

湍流模型选用RNGk-ε模型，该模型体现出了小尺度运动的影响，在科学研究和工程实际中都得到了广泛的应用.

2.2 边界条件

进口条件：采用速度入口以控制轴向雷诺数.出口条件：采用压力出口边界条件，出口设置总压50 000 Pa.壁面条件：无滑移.

求解器选用Fluent，介质常温清水.

2.3 参数定义

轴向雷诺数计算公式为

Ra=2vcρ/μ，

(6)

式中：v为平均轴向速度；c为密封间隙；ρ为密度；μ为动力黏度.

参照文献[2]并重新定义摩擦因数，即

(7)

式中：pin为螺旋密封进口静压；pex为螺旋密封出口静压；L为密封长度.

3 计算结果与分析

3.1 螺旋角和相对槽宽对螺旋密封性能的影响分析

图5为不同螺旋角下的螺旋密封摩擦因数特性曲线，从图5a可以看出，随着轴向雷诺数增大，不同螺旋角下螺旋密封的摩擦因数逐渐减小且趋于收敛，螺旋角为21.05°时摩擦因数最大.从图5b可以看出，随着螺旋角增大，摩擦因数先增大后减小.这是因为当螺旋角越小时，螺旋密封对介质的泵送作用越弱，因此在一定范围内增大螺旋角有利于提升密封性能；由螺旋密封几何关系式可知，螺旋角增大时，有效螺旋槽宽也相应增大，这会使螺旋槽道上附着的介质减少，当螺旋角过大时泵送作用便会减弱.因此，存在最优螺旋角，由模拟结果可知，当螺旋角为21.05°，螺旋密封性能最好.

图5 螺旋密封摩擦因数特性曲线

图6为不同螺旋角下螺旋槽道内的压力psc分布.可以看出，压力从密封进口到出口逐渐降低，螺旋角为21.05°时密封两端压差比其他螺旋角时高，螺旋角由5°增大到30°的过程中，螺旋槽道内的压力先增大后减小，说明螺旋角变化对螺旋槽道内的压力分布有显著影响.

图6 螺旋槽道内压力分布

图7为螺旋密封0.5倍密封长度横截面压力pis和湍动能ε分布.从图7a可以看出，由于螺旋槽道对密封介质的挤压，横截面压力的最大值出现在螺旋槽道的末端，螺旋角由5°增大到30°的过程中，压力呈先增大后减小的趋势.从图7b可以看出，随着螺旋角变化，湍动能分布存在明显差异，湍流脉动剧烈程度不同.螺旋角为21.05°时湍动能最大.

图8为不同相对槽宽下螺旋密封摩擦因数特性曲线，从图8a可以看出，当轴向雷诺数增大时，不同相对槽宽下摩擦因数逐渐减小且趋于收敛，相对槽宽为0.5时摩擦因数最大.从图8b可以看出，随着相对槽宽增大，摩擦因数先增大后减小.这是因为当螺旋槽道的宽度变小时，通流面积也相应减小，介质沿螺旋槽泄漏的阻力增大，有利于减小泄漏量；当螺旋槽道的宽度过大，螺旋槽道两侧旋转壁面对螺旋槽道中间位置处介质的剪切作用将减弱，泵送效果将会变差.因此，存在最优相对槽宽，由模拟结果可知，当相对槽宽为0.5时，螺旋密封性能最好.

图7 螺旋密封0.5倍密封长度横截面压力和湍动能分布

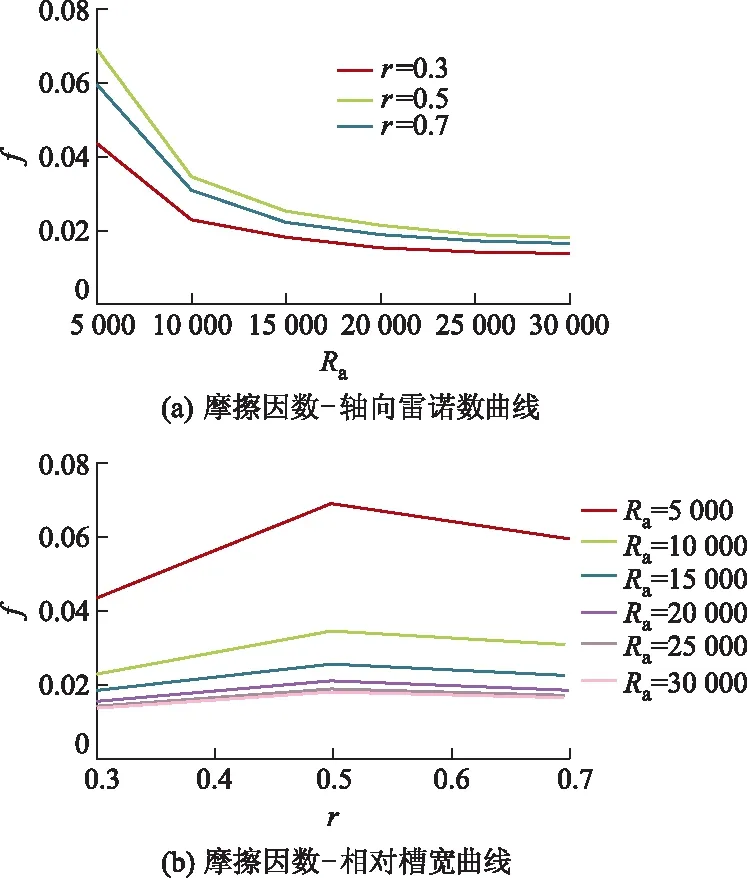
图8 螺旋密封摩擦因数特性曲线

图9为不同相对槽宽下螺旋密封螺旋槽道内的压力分布.从图中可以看出，压力分布很规则，压力最大值出现在密封进口，且压力从密封进口到出口逐渐降低，相对槽宽为0.5的螺旋槽道内压差最大，不同相对槽宽下螺旋槽道内的压力分布有很大差异.

图9 螺旋槽道内压力分布

图10为螺旋密封0.5倍密封长度横截面压力和湍动能分布.从图10a可以看出，相对槽宽影响螺旋密封在所示流域内的压力分布，整体上相对槽宽为0.5时螺旋槽道内的压力最高.从图10b可以看出，随着相对槽宽变化，湍流脉动剧烈程度也不同，相对槽宽为0.5的螺旋密封湍动能最大.

图10 螺旋密封0.5倍密封长度横截面压力和湍动能分布

3.2 相对槽深对螺旋密封性能的影响

控制其他影响因素一定，h+c=0.75 mm，改变相对槽深.如图11所示为不同相对槽深下螺旋密封的摩擦因数特性曲线，从图11a可以看出，当轴向雷诺数增大时，摩擦因数逐渐减小且趋于收敛，相对槽深为3时摩擦因数最大.从图11b可以看出，随着相对槽深增大，摩擦因数先增大后减小.这是因为h+c一定，相对槽深增大时，一方面密封间隙减小，间隙对介质泄漏的阻力增大，另一方面螺旋槽深增大，通流面积也相应增大，螺旋槽对介质泄漏的阻力减小.因此，存在最优相对槽深，由模拟结果可知，相对槽深为3时，螺旋密封性能最好.

图11 螺旋密封摩擦因数特性曲线

图12为螺旋槽道内的压力分布.图13为0.5倍密封长度横截面压力和湍动能分布.

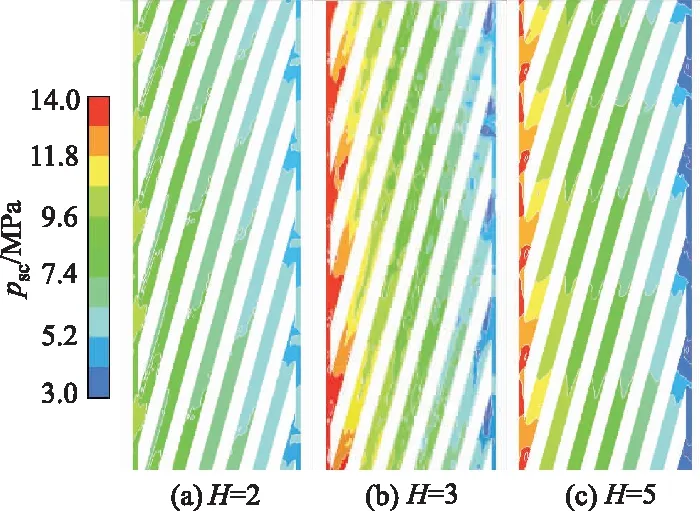
图12 螺旋槽道内压力分布

图13 0.5倍密封长度横截面压力和湍动能分布

Fig.13 Pressure and turbulent kinetic energy con-tours in cross-section at 0.5 axial length

从图12可以看出，相对槽深变化影响螺旋槽道内的压力分布，相对槽深为3时螺旋槽道内压差最大.从图13a可以看出，压力最大值出现在螺旋槽道末端，相对槽深为3时压力明显高于其他情形.从图13b可以看出，随着相对槽宽变化，湍动能分布发生变化，湍流脉动剧烈程度也不同，相对槽深为3的螺旋密封湍动能最大.

4 结 论

通过对不同螺旋密封模型内部流场的数值模拟，从摩擦因数的角度研究了螺旋角、相对槽宽和相对槽深对螺旋密封性能的影响，得到如下结论：

1) 轴向雷诺数对螺旋密封的性能有一定影响，轴向雷诺数增大时密封性能变差，在高轴向雷诺数区，密封性能受轴向雷诺数变化的影响很小.

2) 在其他影响因素一致的情况下，螺旋角、相对槽宽和相对槽深对螺旋密封性能有显著的影响.螺旋角增大时，摩擦因数呈现出先增大后减小的趋势，在最优螺旋角下螺旋密封的摩擦因数最大.相对槽宽增大时，摩擦因数呈现出先增大后减小的趋势，在最优相对槽宽下螺旋密封的摩擦因数最大.相对槽深增大时，摩擦因数呈现出先增大后减小的趋势，在最优相对槽宽下螺旋密封的摩擦因数最大.因此，在设计螺旋密封时需要选择合理的参数.

致谢：本论文得到重庆水泵厂有限责任公司合作委托项目资助.