基于CFD的斜三通管水力特性分析及流场计算

2020-12-04许虎吴文勇王振华王秋良

排灌机械工程学报 2020年11期

许虎，吴文勇，2*，王振华,王秋良

(1. 石河子大学水利建筑工程学院，新疆石河子 832000； 2. 中国水利水电科学研究院，北京 100048； 3. 深圳市广汇源环境水务有限公司，广东深圳 518000)

三通管件在水利建筑行业、农田灌溉、城市生活用水饮水及排污等方面应用广泛.斜直三通管能作为分流管件在管道输配水系统起到重要的作用.水流在三通管内流动的过程中由于边界条件的变化，使得内部流场发生改变，产生强烈的紊动而消耗大量能量.造成水头损失、取水首部需要动力源较大、管道系统运行不稳定等问题.在实际的管道输水工程中，由于三通管夹角的存在，出水口会因为管间夹角的变化而产生不同大小的局部水头损失.管间夹角对于出流能力的影响直接决定了管道输水过程中的输水效率高低.

随着计算流体力学的发展以及计算机性能的提升，数值模拟软件的应用成为流体试验研究分析的重要工具[1].近年来国内外学者对三通管进行试验和数值模拟，得出各种工况下三通管内部压强、温度、流态、局部水头损失等试验结果.

孙鑫[2]通过对T形、Y形、圆弧形三通管进行数值模拟研究，通过压力、流速分布和能量损失计算，得到圆弧形和Y形三通管水头损失较小，T形水头损失最大且水流运动紊乱.朱锦霞等[3]对三通管阀门进行试验和数值模拟，阐明了阀门关闭的时间与管道所受水击压强大小、阀门开度与流量系数关系.石喜等[4]通过对三通管设置不同的分流比，揭示了内部流场分布特性及局部阻力系数与雷诺数、管径比的变化关系.卢冬华等[5]通过数值模拟不同夹角、不同流速比、不同支管位置下的斜三通管内部流动及传热过程，提出支管位置对壁面平均换热系数影响最大、流速比次之、管间夹角最小.刘沛清等[6]通过对抽水蓄能电站的三岔管水流特性数值模拟分析，得出不同工况下分流比、分岔角对岔管水头损失影响.

目前，市场中以90°三通管居多，而对于特殊夹角(30°，45°，60°，120°，135°，150°)的三通管却很少涉及.由于三通管边界条件复杂，仅仅依靠理论和试验分析将会造成很大成本，并且很难将管道水流内部形态、紊乱形成机理清晰地描述.因而，文中通过对不同夹角的斜直三通管数值计算，得出不同进口雷诺数下夹角θ与局部水头损失ζ关系曲线，并直观显示不同夹角管道内部水流形态、各部位流速及压强分布，为特殊夹角的三通管设计与研究提供依据.

1 材料与方法

1.1 物理模型

使用建模软件建立斜直三通管几何模型如图1所示.斜直三通管竖直放置分别由进水管、出水管和支管组成，支管和出水管夹角为θ，角度分别为30°,45°,60°,90°,120°,135°,150°.管道内径32 mm，壁厚为2 mm，为了保证管内水流流态充分发展，压力与速度计算断面取进水管后2倍管径处作为上游断面，出水管、支管前1～2倍管径处作为下游断面[7].

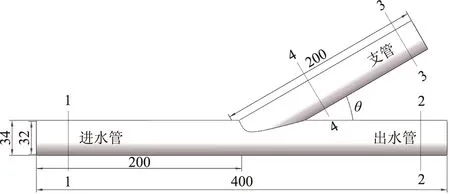
图1 几何模型

入口水流速度分别设置为v1=0.2 m/s，v2=0.4 m/s，v3=0.8 m/s，v4=1.6 m/s，v5=3.2 m/s，v6=6.4 m/s.水体温度为20 ℃，运动黏度νi=1.003×10-6m2/s.相应雷诺数为Re1=31 904，Re2=63 808，Re3=127 616，Re4=255 232，Re5=510 464，Re6=1 020 928.计算式为

(1)

式中：Re为雷诺数；v为管道平均流速，m/s；d为管道内径，m；ν为运动黏滞系数，m2/s.

1.2 计算数学模型

由于标准k-ε模型对于分岔流动具有较高的准确性与试验结果偏差较小，此次模拟计算采用标准k-ε模型.在关于湍动能k方程基础上，引入关于湍动耗散率ε的方程，即为k-ε双方程模型.

湍动耗散率ε表示为

(2)

湍动黏度μi可表示为

(3)

标准k-ε模型的输运方程为

(4)

(5)

式中：Cμ为经验常数；Gk为平均速度梯度引起的湍动能k的产生项；Gb为浮力引起的湍动能k的产生项；Ym为可压缩湍流脉动膨胀对总的耗散率的影响；C1ε，C2ε，C3ε为经验常数，分别为1.44，1.92，0.09；σk，σε分别为湍动能和湍动耗散率对应的普朗特数，分别为1.0，1.3；Sk，Sε为用户定义的源相.

1.3 网格划分

非结构四面体网格具有划分简便、适应性强等特点，本次采用非结构网格划分，在网格划分过程中对于模型交界处和管壁处进行网格加密以保证网格整体质量，提高计算精度.

网格划分如图2所示，为验证网格单元个数与网格质量的联系，以逐渐加密的方式生成网格并检验其质量，如图3所示，M为网格单元质量0.5以上所占整体风格比重.发现当网格单元个数达到一定数值后再增加网格数量反而会降低网格质量.

7种模型分别生成网格个数见表1，网格质量基本在0.5以上且满足计算精度要求.

图2 网格划分

图3 网格无关性分析

表1 不同夹角下网格单元个数

1.4 数值求解方法与边界条件

求解模型采用三维稳态模型，Y方向设置重力9.8 m/s2.进水管设为速度入口，水力直径为0.016 m，出水管和支管设为自由出流.流场采用基于压力修正法的SIMPLE算法迭代计算，压强采取一阶迎风格式、动量和能量方程离散格式均采取二阶迎风格式.残差收敛值为0.000 1，迭代步数为2 000步.

2 结果与分析

2.1 模型可行性分析

为了验证标准k-ε模型对于数值模拟试验的准确性.选取参考文献[8]中的2种工况对模型设置相同的边界条件进行数值计算，并将计算结果与参考文献中的试验结果进行比对，分析其误差σ.如表2所示，表中P1,P2为支管单独供水.文献试验所测局部水头损失与数值模拟计算所得结果误差全部小于10%.表明所选标准k-ε模型可以应用到该模型三通管的数值模拟计算，并具有较高精度.

表2 4种工况下局部水头损失试验值与数值模拟值

2.2 局部水头损失计算

对斜直三通管水头损失进行计算.取进水管至出水管为断面1-2，进水管至支管为断面1-3,其断面能量守恒方程为

(6)

(7)

式中：α为动能修正系数，通常取α≈1.0；ρ为水体密度，103kg/m3；λ为沿程阻力系数；l为管线长度，m；d为管径，m；ΔP13,ΔP12为断面1-3和断面1-2之间的局部水头损失，计算式为

(8)

(9)

式中：ζ13,ζ12为断面1-3,1-2间局部阻力系数.

图4,5为断面局部水头损失系数，从图中可以看出，相同夹角下，局部水头损失随雷诺数增大而减少，当θ值大于90°后增加的趋势更加强烈，这是因为当θ值小于90°时，水流从进水管流向支管的方向与主流的方向一致，在此过程中水流仅需要克服壁面摩擦力、重力、黏滞力做工消耗机械能；当θ值大于90°时，水流从进水管流向支管的方向与主流的方向相反，在此过程中水流因流向改变而额外消耗能量.并且随着夹角的增大水流流向改变越来越明显，水流动能消耗的也越多，局部水头损失系数ζ13增大的趋势越强烈.相同的雷诺数下，ζ13随着夹角增大而增大，ζ12随着雷诺数增大而减小，ζ12在雷诺数大于127 616之后呈现缓慢降低的趋势，并且降低的趋势越来越小，逐渐趋向于稳定[9].当θ小于90°时，支管内单元水流重力分力为2个部分，其中一部分垂直于管壁斜向下方，另一部分平行于管壁斜向下方并且与出水管水流方向相反，此时支管水流有阻碍进水管水流流向出水管的趋势；当θ大于90°时支管内单元水流的重力分力为2个部分，其中一部分垂直壁面斜向下方，另一部分平行于管壁斜向下方，并且与出水管水流方向相同.此时支管水流有推动进水管水流流向出水管的趋势，即出现出水管的水流被支管水流加速现象.水流过流能力随着夹角θ的增大而增大，局部水头损失系数ζ12随着夹角θ的增大而减小.

图4 断面1-3局部水头损失系数ζ13

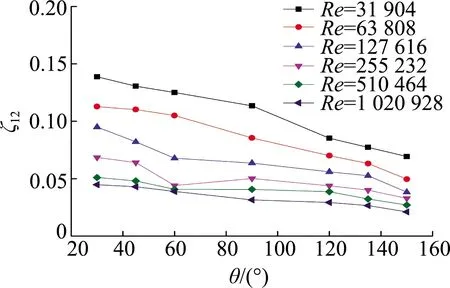
图5 断面1-2局部水头损失系数ζ12

表3为不同进口雷诺数下断面1-3局部水头损失系数ζ13和断面1-2局部水头损失系数ζ12与夹角θ之间的函数关系表达式，断面1-3与断面1-2局部阻力系数均与夹角呈现较好的一次线性关系.ζ12与夹角θ呈现负相关，ζ13与夹角θ呈现正相关，且两者相关性较强，说明回归模型具有可靠性.

表3 不同雷诺数下局部水头损失系数ζ与夹角θ之间函数表达式

2.3 压力云图

图6分别为进口雷诺数Re=255 232时，不同夹角下压力云图分布情况.夹角θ逐渐增大的过程中，进水管处压强一直处于均匀分布状态，夹角的改变对于进水管压强分布影响较小.出水管处压强有降低的趋势，但变化程度较小.支管处压强有明显的随着夹角θ增大而降低的趋势，当夹角θ小于90°时，支管处压强呈现均匀分布状态；当夹角θ等于90°时，支管水流方向垂直于主流方向，水流流出支管时因承受重力而变得困难.支管处压强变低，在主管与支管的交界处出现负压；当夹角θ大于90°时，支管水流因承受重力和改变水流流向的因素，水流流出支管变得十分困难.支管水流有产生回流、倒流的倾向，水流在主管与支管的交界处做无规律旋转、掺混.整个支管出现负压，压力极小处位于主管与支管的交界处.

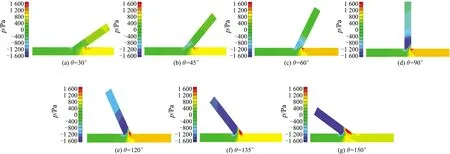
图6 Re=255 232时不同夹角压力云图

2.4 流线及速度云图

图7分别为进口雷诺数Re=255 232时，不同夹角下流线及速度分布情况.进水管速度分布较为均匀，基本不随夹角的改变出现变化.由于分流的原因，水流流速在出水管与支管内变低，总体呈现为出水管内水流流速略大于支管内水流流速.流体存在易流动的特性，水流在流动过程中具有抵抗剪切变形的能力，在垂直于流动方向上便产生了速度梯度，靠近壁面的水流流速略低于远离边界层水流流速.水流从进水管流向支管的过程中随着夹角θ的增大，水流流态变得越来越复杂.当夹角θ值为30°,45°,60°时，水流流线较为简单旋涡比较清晰；当夹角θ为90°,120°时旋涡开始出现凌乱、不成形的趋势；当夹角θ为135°,150°时水流开始无规则的碰撞、回流、旋转.此时水流掺混最为强烈，流态最不稳定，消耗的机械能最多，局部阻力损失最大.

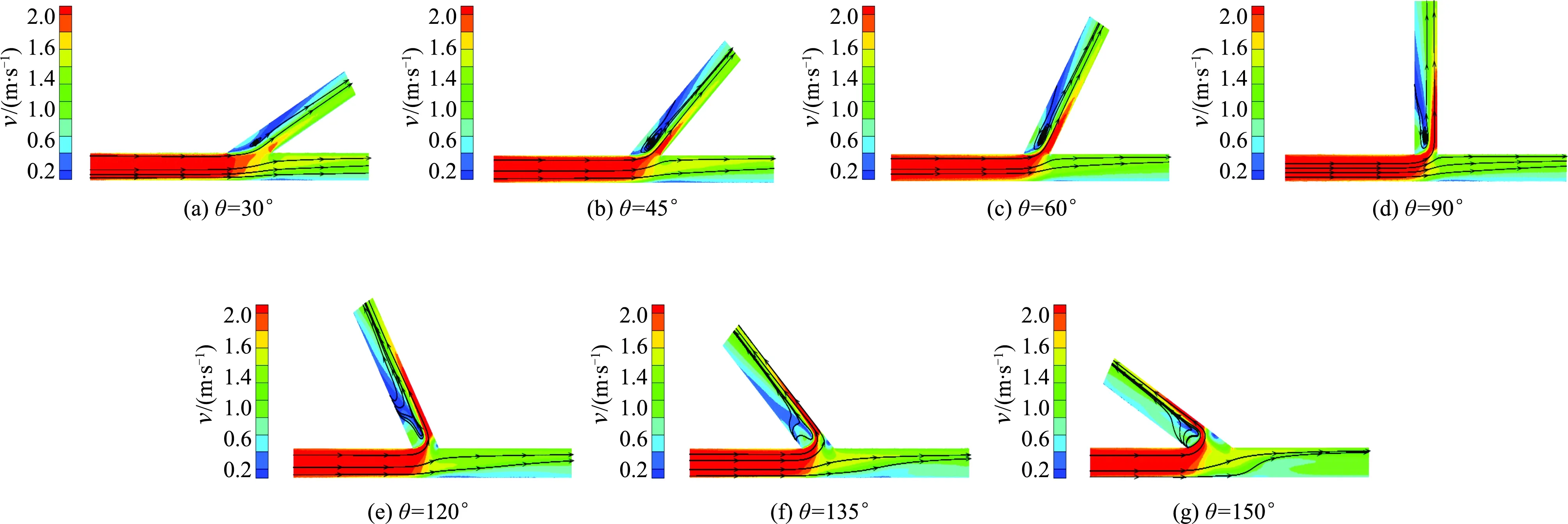
图7 Re=255 232时不同夹角流线分布及速度云图

2.5 湍动能分布云图

为探究三通管内出水管与支管交界处湍动能分布情况，取距交界处1倍管径且平行于支管方向断面4-4作为计算断面.计算公式为

(10)

(11)

式中:I为湍流强度；U为平均流速,m/s

图8为Re=255 232时不同夹角下支管断面湍动能k值，且随着夹角θ增大呈现增大的趋势.当边界条件一定时，湍流强度随着雷诺数的增大而减小.当雷诺数大小一定时，湍流强度随着边界条件的改变而改变.夹角θ小于90°时，支管水流方向与主流方向一致，此时支管内水流流态较为稳定.分子间能量传递较少湍动能及湍动能耗散率较低[10].夹角θ为90°时，支管水流垂直于主流向上，此时重力成为阻碍水流流动的主要障碍，支管内水流开始无规则的旋转并与壁面碰撞.分子间能量的传递逐渐加剧湍动能及湍动耗散率增大.夹角θ大于90°时，由于支管水流方向与主流方向相反，水流流态愈加复杂、紊乱.分子间相互碰撞摩擦，加剧能量的传递与消耗，此时断面湍动能达到最大化，局部水头损失与能量的消耗也最大.湍动能随着夹角的增大而增大，夹角小于90°时湍动能数值及变化程度较小，夹角为90°时湍动能发生显著增长，此时水体所受重力分力最大，重力成阻碍水流出流的主要因素.夹角大于90°时湍动能持续增大，此时水体所受重力分力变小，因流向改变产生的阻力不断增大，是湍动能增大的根本原因.可以得出结论：因支管夹角改变造成的水流流向改变，是影响三通管出流能力的主要原因.

3 讨论

对于直管而言，当水流型态为紊流时，沿程阻力系数随着雷诺数Re的增大由紊流光滑区过渡到紊流粗糙区，黏性底层厚度和雷诺数呈负相关关系.当雷诺数增大到一定程度之后黏性底层所产生的黏滞阻力基本可以不用考虑，此时对沿程阻力系数的影响因素为管壁的粗糙度.石喜等[4]对2种三通管进行研究得出局部阻力系数在雷诺数大于1.00×105之后趋于稳定，此时水流进入到紊流粗糙区.由图3,4得出结论当雷诺数大于1.27×105水流开始进入紊流粗糙区，此时雷诺数对于局部阻力系数的影响可以忽略.管道输水过程中局部阻力损失一般会出现在等径管道的转弯处或者非等径管道的突扩、突缩段.水流型态与内部结构随着固体边界形状的改变而发生改变，水流产生旋涡和脱离壁面现象[11-12].此时水流中各液体质点发生无规律的碰撞、摩擦，机械能转为内能.当夹角θ值较小时，进水管至支管方向的水流方向和主流方向一致，此时局部阻力损失仅仅考虑克服重力、黏滞力做工所消耗掉的部分能量.水流流态较为稳定并且对进水管至出水管的水流影响较小；当夹角θ逐渐增大时，进水管至支管的水流方向与主流的方向相反，此时的阻力损失要考虑因克服水流方向改变而额外消耗的能量，由于消耗大量的机械能水流流出管道的能力变弱，开始出现大量回流以及不规则的旋涡.