湍流发生器径比对剪切室内流体黏度的影响

2020-12-04刘在伦王虎芦维强苏丹枫

排灌机械工程学报 2020年11期

刘在伦，王虎，芦维强，苏丹枫

(1. 兰州理工大学能源与动力工程学院，甘肃兰州 730050； 2. 兰州理工大学温州泵阀工程研究院，浙江温州 325105； 3. 重庆三峡学院环境与化学工程学院，重庆404000)

在中浓纸浆泵中，湍流发生器位于泵入口位置，其主要作用是在泵入口提供1个高剪切流场，在流场内通过旋转剪切作用，使中浓纸浆进入叶轮前湍流化，从而增加浆液的可流动性，实现中浓度纸浆的运输.梁晓瑜[1]指出，中浓纸浆(7%≤C≤15%)在高剪切流场中实现湍流化后可用中浓纸浆泵输送.叶道星等[2]通过试验测量，发现中浓度纸浆湍流化过程存在湍流化前与湍流化后2个阶段，且湍流发生器的外径与纸浆性质、湍流化点及对应的剪切速率、中浓纸浆泵的转速有直接关系.李红等[3]采用Fluent内嵌Heschel-Bulkley流体模型，数值模拟得出通过减小输送管道直径以接近于湍流发生器叶轮外径的方法，实现纸浆的湍流化.叶道星等[4]基于声纳流量测试系统，设计了1种中浓度纸浆泵性能试验台，发现中浓纸浆泵的扬程、效率随着纸浆浓度的增加逐渐下降.叶道星等[5]提出了正交试验可用于纸浆泵性能的优化.李智等[6]根据中浓纸浆的流动特性，推导了湍流发生器外径的计算方法.李瑞瑞等[7]采用试验研究，分析提出了螺旋叶片式湍流发生器有效剪切速度的概念，优化了螺旋叶片式湍流临界转速的计算公式，验证了湍流临界转速不仅与叶片直径有关，还与叶片的螺旋升角、螺距密切相关.目前，国内外专家学者针对湍流发生器进行的试验与数值计算还比较少，关于剪切室内流体黏度的研究尚不完善.因此，探究湍流发生器剪切流场内流体黏度的变化规律具有重要意义.

文中提出1种中浓纸浆泵湍流发生器的新型设计方法，设计5种不同径比的湍流发生器方案，采用数值计算方法，通过改变径比系数e，研究不同径比条件下剪切室内流体黏度的变化规律.

1 湍流发生器的设计

1.1 设计思想与径比的定义

实现湍流发生器与纸浆泵的合理过渡是湍流发生器设计的关键.针对独立结构的湍流发生器，相比整体式结构，其优点是可以与叶轮进口保持适当的距离，便于湍流化的纸浆浆液在进入叶轮前实现气体的排除，且与螺旋式湍流发生器相比具有更紧凑的结构.如图1所示，湍流发生器安装在纸浆泵进口，实际运转过程中应与纸浆泵相互匹配.

泵入口直径是直接与流量相关的参数，计算公式为

(1)

式中：v1为离心纸浆泵进口流速，在离心泵设计中一般取3 m/s；Q为泵设计流量，m3/s；Dj为泵入口直径，m.

为了将湍流发生器和纸浆泵从水力和结构上系统地联系起来，以纸浆泵入口直径Dj为基准，对中浓纸浆泵湍流发生器进行量纲一参数化设计，引入了径比e的定义，计算公式为

(2)

式中：D为湍流发生器外径，m.

1.2 叶片型线的确定

湍流发生器叶顶型线在外径为D的圆周面上，在确定包角α后，将直径为D的圆周面按图2所示的方格区域截取出来，展开后便得到叶轮外径为D、包角为α的方格网参数控制图，如图3所示.

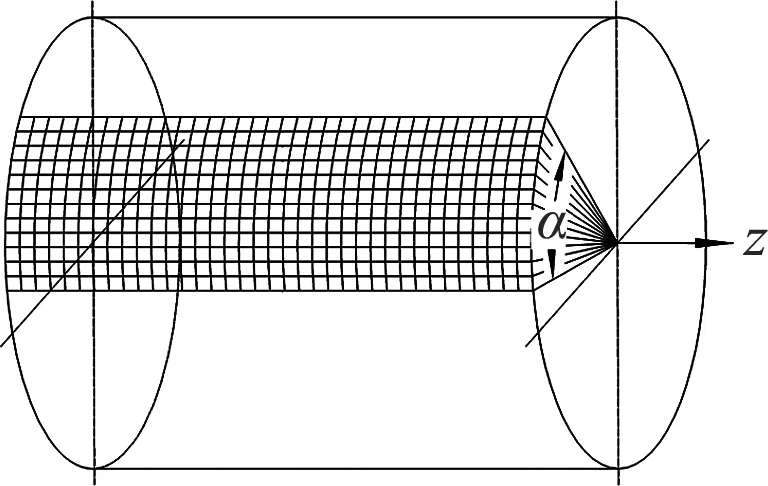
图2 圆周面方格网示意图

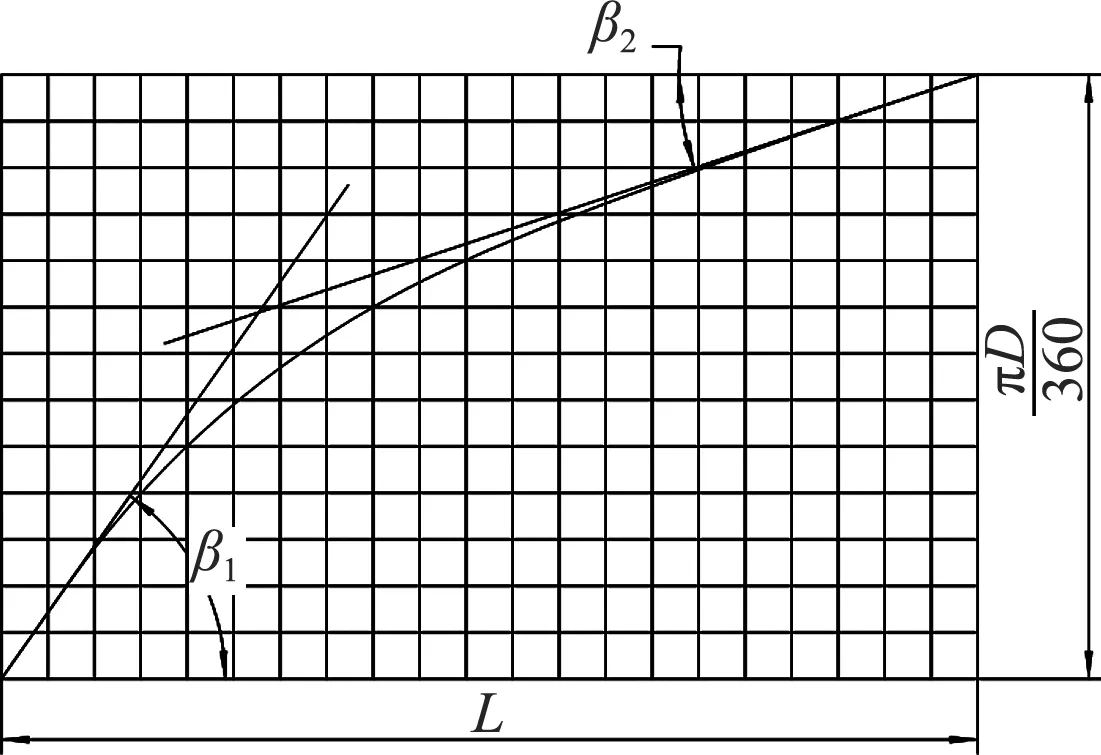
图3 型线方格网示意图

1.3 湍流发生器的几何尺寸及模型

以150XJ125-25型无堵塞纸浆泵的入口直径Dj=150 mm作为设计条件，根据以上的设计思路和方法，确定出湍流发生器的基本参数:入口角β1=42°，包角α=40°，出口角β2=16°，轴向总长L=70 mm，叶片伸出段L1=25 mm，叶片轮毂直径d=53 mm，叶片厚度λ=5 mm.

其他参数不变，取湍流发生器径比e为0.5,0.6,0.7,0.8,0.9，对应三维实体模型如图4所示.

图4 湍流发生器三维实体模型

2 H-B流体模型及纸浆物性参数

Heschel-Bulkley(简称H-B)流体模型是由宾汉流体和幂律流体组合的非牛顿流体模型，可以表现出剪切稀化或剪切增稠行为，n>1时表现为剪切增稠，n<1表现为剪切稀化，其本构方程为

(3)

H-B模型数学通常用于描述混凝土、纸浆、泥浆、面团和牙膏等非牛顿流体,计算公式为

(4)

(5)

式中：μ为动力黏度，Pa·s；γ为剪切速率，s-1；γc为临界剪切速率，s-1.

当γ<γc时，剪切应力和剪切速率之间变化可描述为幂指函数；当γ>γc后，其剪切应力与剪切速率可近似为线性关系[8].中浓纸浆是一种具有屈服极限的剪切稀化流体，只有当流动产生的剪切力大于自身的屈服极限时，纸浆才会流动.在不同剪切力作用下，其黏度的变化满足H-B流体模型中n<1的情形，当剪切速率大于临界剪切速率时，中浓纸浆被湍流化，其黏度变化近似地按牛顿流体处理[9].

3 数值计算

在纸浆泵入口直径为150 mm的情况下，保持其他几何参数不变，仅改变外径，并建立不同结构的几何模型.全流道区域均采用高质量的六面体结构化网格划分，如图5所示.

选择适用于计算速度梯度较大、考虑旋转效应以及可计算低雷诺数效应的RNGk-ε湍流模型[10]，设置进口边界条件为速度进口v=2 m/s，出口边界条件为outflow，转速n=1 450 r/min.固壁面采用无滑移边界条件，近壁面采用标准壁面函数法处理，控制方程为连续性方程和基于雷诺时均RANS的动量守恒方程，采用在通量修正方法上改进后的SIMPLEC算法，收敛精度设为10-4.采用Fluent内与温度无关的H-B流体模型，取浓度为12.5%的卫生纸浆为模拟介质，根据文献[11]对12.5%卫生纸浆剪切特性的试验结果，将H-B流体参数设置为屈服应力τy=936 Pa，浓度系数k=204 Pa·s，剪切稀化指数为n=0.08，取临界剪切速率γc=200 s-1.模拟中黏度数量级与试验结果相一致[12].通过数值模拟的方法，分析湍流发生器径比对剪切室内流体黏度的影响，进而找出合理的径比e取值范围.

图5 湍流发生器流动区域网格划分

4 结果与分析

4.1 径比对轴向截面内黏度分布的影响

图6为轴向截面位置示意图，取Z为10，30和70 mm共3个轴向截面，观察其黏度与径比的变化规律.在Z=10 mm轴向截面内，径比e由0.5增大至0.9过程中，截面上高黏度区域逐渐减小，而在径比e=0.8～0.9，靠近轮毂的高黏度区域逐渐增大，且轮缘叶顶部位出现高黏度流体；在Z=30 mm轴向截面内，径比e由0.5增加至0.9过程中，低黏度流体所占区域在此截面内不断扩大，截面内靠近轮毂的高黏度区域逐渐增大；在Z=70 mm轴向截面内，径比e=0.5～0.9的变化时，可以观察到其上低黏度流体区域逐渐增大，且截面内靠近轮毂的高黏度区域逐渐减小.

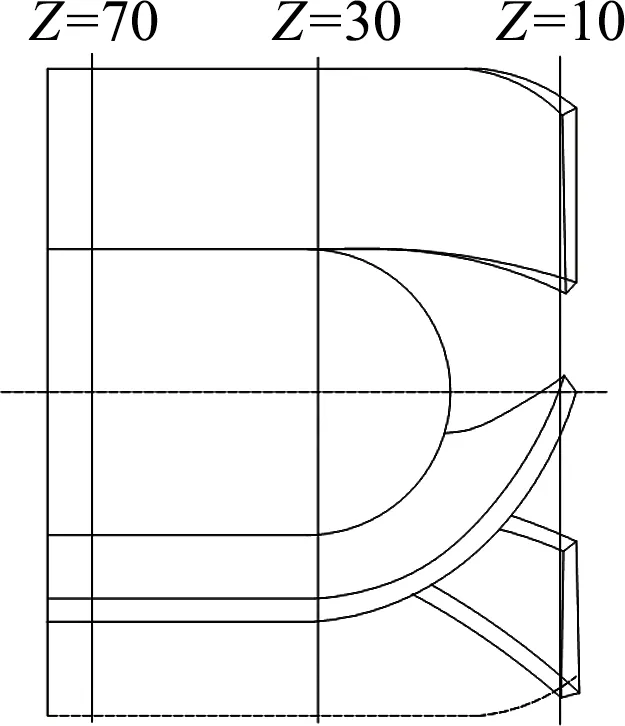
图6 轴向截面位置示意图

从流体力学的角度分析，径比e较小时，剪切室内仅湍流发生器叶片周围的流体获得较大的剪切速率，使得黏度降低，而湍流发生器叶顶与管壁之间的流体所受剪切速率很小，仍保持较高的黏度[13].在径比增大的过程中，湍流发生器叶顶与管壁的距离逐渐减小，靠近管壁的流体所获剪切速率逐渐增大，使得靠近管壁的低黏度区域逐渐增大.如图7所示，湍流发生器主要由叶片表面和叶顶为流体提供高剪切流场，径比增大后，靠近轮毂且离叶片较远的流体，所受剪切速率逐渐减小.文中设计的湍流发生器进口部位叶片弯扭程度较大，因此叶片对流体所做的功没有完全用来提供高剪切速率，导致剪切室进口至中间轴向截面上该部分流体的黏度增大，出现了明显的高低黏度分离现象.而在剪切室出口位置处，叶片对流体所做的功几乎完全用来提供高剪切速率，因此，在径比增大时，剪切室出口位置流体的黏度逐渐降低.

图7 不同径比下过流断面黏度分布

4.2 径比对黏度均值和标准差的影响

以统计学的思想引入黏度均值和黏度标准差作为评价湍流发生器性能的参数，其计算公式为

(6)

(7)

通过观察剪切室内的黏度云图，发现其黏度变化为中心轴对称分布，每隔120°为1个周期.因此，取包含单个叶片的120°剪切区域为研究对象，在整个剪切室内各个部位均匀设置了105个监测点，如图8所示，并获取其黏度值.

图8 剪切室监测点分布示意图

监测点黏度平均值是以更直观的数值方式反映剪切室内流体黏度的整体值，黏度标准差则表示各个监测点的黏度值与平均值的远近程度.如图9所示，在径比e不断增大过程中，湍流发生器剪切室内所设监测点黏度平均值曲线呈逐渐减小趋势，其值由234.01 降至199.73 Pa·s.随着径比的增大，剪切室内黏度均值降低，说明在已设计的5种湍流发生器中，单从黏度整体值降低的角度，大半径的湍流发生器是对湍流化有利的.监测点黏度标准差曲线呈先降低后增大的趋势，径比在0.5～0.7，黏度标准差由97.26 Pa·s降低至86.18 Pa·s，在0.7～0.9，黏度标准差又从86.18 Pa·s增加到96.60 Pa·s，最低点在e=0.7附近.随着径比的增大，湍流发生器提供更大的剪切速率，使得剪切室内黏度均值降低，但同时导致了高低黏度的分离现象，使得剪切室内黏度分布的不均匀程度增加.

图9 黏度均值、标准差随径比e的变化

4.3 剪切室内黏度的径向分布

如图10a所示，径比由0.5增至0.9时，黏度大于300 Pa·s的等值体逐渐减小，剪切室小半径区域的高黏度等值体增大，在大半径区域高黏度等值体减小；黏度小于100 Pa·s的等值体逐渐增大，剪切室内低黏度等值体沿径向逐渐增大，在大半径区域高黏度等值体减小，如图10b所示.

图10 不同径比下剪切室内黏度等值体的分布

为了更进一步研究径比对剪切室内黏度径向分布的影响，在Z=10，30，50，70 mm的轴向截面内120°轴对称区域，取4条径向直线L1，L2，L3，L4，其中L1位于湍流发生器叶片压力面，如图11所示.

图11 径向直径分布示意图

图12为各个轴向截面内，径比对剪切室内黏度径向分布的影响.从图中可以看出，在Z=10 mm轴向截面内，半径增大的过程中，L1，L2，L3，L4上黏度曲线在半径10 mm处有极小值，约为150 Pa·s，且半径r在0～20 mm，不同径比下的黏度曲线接近重合，这表明剪切室内进口小半径处黏度的变化几乎不受径比影响.其原因是，剪切室进口因湍流发生器叶片延伸段的存在，使小半径区域内剪切速率较大，径比变化时，叶片延伸段的内径dj并没有改变.说明在剪切室内的高剪切区域位于叶片表面或叶片边缘处，因此可以通过增大叶片延伸段内径，以降低剪切室进口黏度的不均匀性.

图12 各个轴向截面内，径比对剪切室内黏度径向分布的影响

在Z=30和50 mm轴向截面内，黏度最低点位于最大和最小半径位置处，曲线中间部位存在极值，并逐渐沿半径增大方向移动.L1上存在黏度最小值点，对应黏度值约为50 Pa·s，此点随径比的增大，逐渐沿半径增大方向移动，这说明叶片周围黏度极小值的位置与径比有关.在Z=70 mm轴向截面内，L1上低黏度范围随径比增大而增大，L2，L3，L4上高黏度范围明显变宽，但在同一半径处，黏度随径比的增大而减小，这表明随径比增大，低黏度区域逐渐沿半径增大方向发生扩散.在剪切室出口位置，同一半径区域的黏度对径比的变化更为敏感，靠近剪切室出口位置的轴向截面上，流体黏度受径比影响较大，且随径比增大而减小，湍流发生器出口部位对流体的湍流化作用较大.因此，湍流发生器叶片包角不易过大，较大的包角会导致叶片过度弯扭，使得剪切室对应部位的剪切速率降低.