Numerical investigation on self-priming process of self-priming pump

, , , , ,

(National Research Center of Pumps, Jiangsu University, Zhenjiang, Jiangsu 212013, China)

Abstract: In order to investigate the self-priming process of the self-priming pump, an unsteady simulation was conducted where the Navier-Stokes equations were used with the Lagrangian-Eularian mo-del. In course of this investigation, the volume fractions, pressure distribution and self-priming time were carried out. By analyzing the volume, velocity and pressure distribution of the gas-liquid two-phase flow at different time, the two-phase content via the variation law of the two-phase flow in the pump was carried out. By monitoring and analyzing the gas-liquid flow at the outlet of the pump, the self-priming time and crucial periods were given. Two phenomena were mainly characterized by the self-priming process such as the gas-liquid mixing and separation, which occur in the early stage of self-priming process. During that period the gas-liquid mixing clouds appear on the outer edge of the impeller, and the instantaneous void fraction at the inlet and outlet of the impeller decreases obviously. It was also established from the transient study that the gas has a major influence on the hydraulic performance of the pump at the early stage of operation. To increase the usage of self-priming pump and to also understand the energy conversion of the pump, it is very essential to investigate and establish the basic working principle of the self-priming pump.

Key words: self-priming pump;self-priming process;numerical simulation

A self-priming centrifugal pump is a common pump that levitates water from one point to another. It is very useful with its ability to prime itself without any human assistance. The main difference between the traditional centrifugal pump and the self-priming centrifugal pump is to start up without pre-irrigation and then to work as a common pump when air in the pump is exhausted[1].

A very complicated internal transient flow accompanies the self-priming process of self-priming centri-fugal pump which is most of the time gas-liquid (air-water in this study).

Compared with the traditional centrifugal pumps, a self-priming centrifugal pump is reliable and conve-nient to use with its robust construction and easy maintenance, it is widely used in agriculture, irrigation, fire protection, water engineering and other fields[2-4].For its more simple structure and higher efficient as no recirculating flow and related components, the outer-mixing self-priming pumps are used almost everywhere in the world.

According to the study done by STEPANOFF[5], the suction pressure is an important variable that controlled the volume entrained-air and a breaking of Head-Capacity curve happens when the volume of those two-phase flows are equal. A mixture of two-phase flow through a pump can also cause friction losses, and the more the percentage of entrained air increases, the more the head efficiency decreases[6]. It is noted that an impeller with short and curved vanes has the best ability to handle air than others, academicians carried out orthogonal test and made an improvement of the performance[7-8]. The influence of gas-liquid separation chamber on the self-priming performance of self-priming centrifugal pump was investigated by an experimented group and concluded that factors are interrelated and mutually restrictive which provide theoreti-cal design guidance, and a new type of outlet vortex chamber is explored with automatic valve[9-11]. SHA, et al.[12-13]studied the influence of the area of the reflux hole, the gap between the tongue and the impeller type on the performance of the self-priming pump through experiments, and put forward the method of improving the self-priming performance through the fluency analysis. LYU, et al.[14]summari-zed and analyzed the development history of self-priming pump, the influencing factors of self-priming performance and including the calculation parameters. LI, et al.[15]installed an integrated circulating jet system on the basis of the ordinary self-priming pump, siphon structure to see internal flow characteristics of pump and carried out hydraulic and self-priming performance tests and they concluded that the mixture speed at inlet that of the two-phase flow separation which improves the pump performance. YANG, et al.[16]through the self-priming performance test, optimized the self-priming pump and improved its perfor-mance by focusing on the the pump parameters.

However, in this paper, modeling the numerical simulation of self-priming centrifugal pump is based on the boundary conditions and void fractions at the suction pipe. Thus, inlet pipe is filled by water with the atmospheric pressure. That void fraction is reduced at the entrance of the pump, and water is sucked when the pump started working. That is why it is convenient to set the initial conditions at the suction pipe for the two-phase flows transient simulation, and the internal flow characteristics will be carried out in course of the self-priming pump process.

1 Configuration of self-priming pump and its overall performance

Fig.1 shows the configuration profile of the pump used in the study, and it is interesting that the volute outlet is downwards that it is also the hole through which the water/liquid separated in the housing flows back to the impeller to maintain the water level merging a majority of the impeller. The pump is obviously an outer-mixing one. The wide tongue is a typical design feature that ensures the mixture is able to be sufficiently separated. Meanwhile the shaft axis is designed lower than the original water level to achieve efficient mixing.

Fig.1 Configuration sketch of self-priming pump and overall performance

The diameter of the pump impeller is 127 mm, and the cascade solidity of the impeller is low as the impeller is designed to treat with flooding sewage that includes stones and clay lumps. First the steady nume-rical simulation was conducted to predict the overall performance of the pump. The numerical work was carried out by the commercial software ANSYS-CFX[17-18]and only the results are displayed in Fig.1 for brief description. The blue line is the Head-Capacity characteristic released by the manufacture, and it is interesting that the line is not a traditional one but nearly a curved line. The manufacturer stated that due to no anti-wear ring installed in the pump, there are large leakage flows that contribute the head deficiency. The rated parameter of the pump undern=2 900 r/min isQ=80 m3/h andH=10.5 m. Basic geometrical parameters of pump is following: impeller inlet diameterD1=81 mm, impeller outlet diameterD2=127 mm, impeller blade numberZ=3,volute basic diameterD3=130 mm, volute inlet widthb3=40 mm.

2 Numerical simulation

2.1 Mathematic models for two-phase flows (air-water)

Lagrangian and Eulerian methods have been used as calculation methods, the Eulerian method, being more complex but general can simulate the flows with a large interval of fraction volume. In other hand, the studied case is a turbulently biphasic flow, also the turbulent model might be properly chosen to be near to the Reynolds Average Navier-Stokes (RANS) equations[19-20].

Continuity equation:

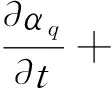
(1)

Momentum equation:

(2)

Phase stress-train tensor:

τq=αqμq(vq+vq[I],

(3)

Reynolds stress tensor:

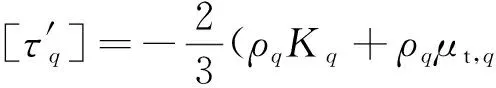
(4)

Turbulent viscosity:

(5)

Turbulent kinetic energyKq:

(6)

Turbulent dissipation ratioεq:

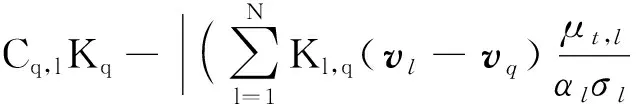
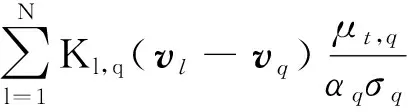
(7)

whereαqthe volume fraction of the flowq;λqandμqare bulk viscosity and shear on acceleration due to the gravity;Kp,qis the coefficient of momentum exchange term for turbulent flows (this term is the exchange of momentum at interface of the two-phase flow where air can be dispersed in water and gotten from differential of the momentum equation).Flift,FqandFvm,qare the lift force, external body force and virtual mass force, respectively.

Equations (1)—(7) constitute the closure formulations for the current simulation. The detailed relevant coefficients in the equations can be referred to Ref.[10].

2.2 Flow domain and mesh generation

The 3D model of this self-priming centrifugal pump was carried out with Pro/E software as shown in Fig.2 with its different parts such as inlet pipe, S-pipe, impeller, volute, reflux-hole, housing and the outlet pipe. For solving the problem the model was imported into the ANSYS ICEM software to generate mesh, but with the complexity of the geometry the unstructured meshes were found out with an acceptable quality 0.35 as shown in Fig.2a. The total mesh elements are 2 615 782.

Fig.2 Flow domain and mesh generation

The pump head at each operating point is evaluated using Eq.(8).

Bernoulli′s equation:

(8)

whereH,p1andp2are the head, inlet and outlet pressure respectively.

2.3 Boundary conditions and initialization

In this study, the pump is initially half filled with water and the rest part with air, in the real working conditions the check valve is considered open without any back flow. The boundary conditions of this research are set at the inlet as total pressure and outlet is defined as opening because of the atmosphere instability, both two-phase flows have a velocity equal to zero. The suction pipe is an elbow shape and 600 mm long to suck water from the suction tank as shown in Fig.2a.

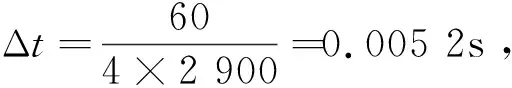
3 CFD results and analysis

3.1 The mass flow rate diagrams

The gas-liquid two-phase flow field is shown in Fig.3 in the vertical plan at different times during the flow process.

Fig.3 Contours of air volume fraction during the self-priming process of self-priming pump

As shown in Fig.3a, initially the pump is filled with water up to the mid impeller and the rest area is constituted of air void fraction, due to the gravity and buoyancy force this is obvious. It can be seen from the Fig.3b that the lower flow enters the inlet impeller, while it enters the liquid storage chamber with high air flow rate, and it mixes at the blades tip by the impeller. Fig.3c shows the moment that most of the gas enters the impeller, is highly mixed with water and the mixture flow goes to the liquid separation chamber where it is separated into two states (liquid/gas) before being exhausted from the pump. From Fig.3c the mixture becomes homogeneous and the following phenomena can be found: ① the gas gathers on the suction side of the impeller blades; ② due to the centrifugal force, the liquid, as the heavier phase, is thrown to the volute wall. The gas, as the lighter phase, concentrates around the impeller outlet and the gas upwards to the pump outlet. An important air void fraction is shown at the blades suction side withαroughly being equal to 1 (pure air) which means the blades suction side are bounded with air because of the rotational speed and the centrifugal force. As shown in Fig.3d, 3e and 3f, two phenomena are mainly characterized by the self-priming process such as the gas-li-quid mixing and separation, which occur in the early stage of self-priming process. During that period the gas-liquid mixing clouds appear on the outer edge of the impeller, and the instantaneous void fraction at the inlet and outlet of the impeller decreases obviously and the fluid mixture from the outlet volute arrives at liquid-gas separation chamber where air exhausts and water flows back into housing due to the gravity force and less pressure is required to providing head, and during the following step water exhausts out from the pump outlet. The self-priming phenomenon takes place when the whole gas is pumped, this corresponds toα=0 at 3.00 s (pure liquid) as shown in Fig.3f.

3.2 Pressure distributions

The pressure distribution in Fig.4 shows that the volute converts the kinetic into pressure energy in collection area due to the increase of the volute section from inlet to outlet.

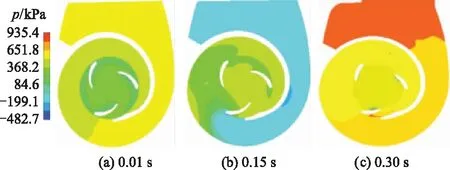
Fig.4 Pressure distribution

It can be seen from Fig.4a that the pressure distribution is much higher at the volute than impeller because of vortices and flow instability. These phenomena are more visible in Fig.4b where the pressure decreases drastically in the mixture process because of the flow instabilities and two-phase flow interaction as shown in Fig.4b. Therefore, from Fig.4c, the pressure is consi-derably increasing because there is no or less air in the pump corresponding to the end of self-priming process, also the instabilities are relatively decreasing and the kinetic energy is converted into the pressure energy. The gap noticed between the experimental and numerical is estimated around 4.47% uncertainties caused by the flow vortices friction losses, recirculation losses, clearance losses, etc.

4 Conclusions and perspectives

This study is very important because the real working conditions can be applied in in the numerical simulation process and the transient of two-phase flow is used to study the internal flow characteristic. To ensure the separation process a pre-irrigation of the pump is necessary. The gas presence in the pump reduces the performance of the pump by consuming more input power. At the early stage the impeller air volume fractions decrease rapidly while those of inlet increase and both fluctuate till zero at 3 s corresponding to the single-phase flow.

The performance of experimental and numerical is consistent with a small gap being approximately equal to 4.4% uncertainties.

From this study, it is found that the pressure distribution was lower in the early stage of self-priming pro-cess. The pressure became higher after the self-priming process since the flow is single-phase flow (water) corresponding to the self-priming time, which is 3 s.

This work can be performed by increasing or decreasing the gas-liquid separation and/or storage chamber and reflux-hole, and modify the shape of blades (short and curved blades).

Acknowledgements

The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: this work was supported by the National Natural Science Foundation of China (Grant No. 51879120).