数据分析素养观下“概率与统计”高考试题研究
——以2017-2019年高考理科数学全国卷为例*
2020-12-03涂冬雪李孝诚淮北师范大学数学科学学院235000
涂冬雪 李孝诚 (淮北师范大学数学科学学院 235000)
1 问题提出
《普通高中数学课程标准(2017年版)》提出了六大数学学科核心素养,强调在数学学习过程中着力发展学生的数学学科核心素养.对于数学高考命题,指出“命题应依据学业质量标准和课程内容,注重对学生数学学科核心素养的考查,处理好数学学科核心素养与知识技能的关系,要充分考虑对教学的积极引导作用.对于每道试题,除了要给出传统的评分标准外,还需要给出反映相关数学学科核心素养的水平划分依据.”[1]
关于“概率与统计”高考试题的研究,总体上以“概率与统计”相关试题的题型分布[2]、考生错误与剖析、考题特点与价值[3]、试题结构等方面进行分析,缺少数据分析素养观下“概率与统计”高考试题的分析.结合我国课程标准对学业质量水平的分析,需要建立数据分析素养观下的试题分析框架,深入分析试题对核心素养的反应情况,显得尤为重要.
2 数据分析素养观下“概率与统计”高考试题分析框架
2.1 “数据分析”核心素养
数据分析是研究随机现象的重要数学技术,是大数据时代数学应用的主要方法,也是“互联网+”相关领域的主要数学方法.课程标准指出,数据分析,是指针对研究对象获取数据,运用数学方法对数据进行整理、分析和推断,形成关于研究对象知识的数学学科核心素养.数据分析过程主要包括:收集数据,整理数据,提取信息,构建模型,进行推理,获得结论.
数据分析素养具体表现为学生通过高中数学课程的学习,能提升获取有价值信息并进行定量分析的意识和能力;适应数字化学习的需要,增强基于数据表达现实问题的意识,形成通过数据认识事物的思维品质;积累依托数据探索数据的本质、关联和规律的活动经验.
2.2 数学学业质量水平
学业质量是指学生在完成本学科课程学习之后的学业成就表现.而学业质量标准是以学科核心素养及其表现水平为主要维度,结合课程内容对学生成就表现的总体刻画.学业质量是学生自主学习与评价、教师教学活动与评价、教材编写的指导性要求,也是相应考试命题的依据.
数学学业质量水平,是指六个数学学科核心素养的综合表现.每一个数学学科核心素养划分为三个水平,都是通过四个方面进行表述(表1).新课标对“数据分析”学科核心素养的三个水平给出了具体表现的描述,分别为水平一、水平二、水平三.每一个水平均是通过上述的四个方面去进行描述.
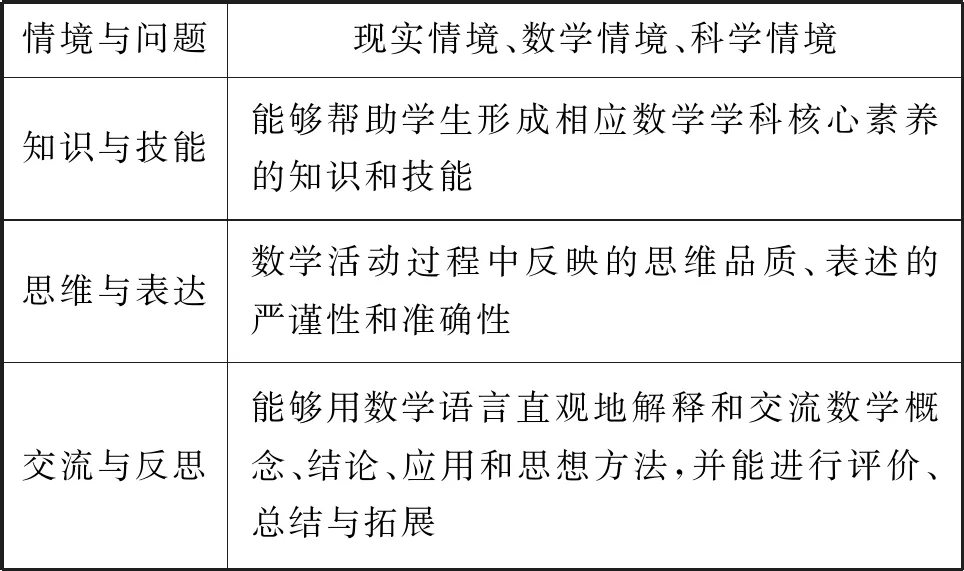
表1
2.3 分析框架
依据《普通高中数学课程标准(2017年版)》对数据分析素养的界定和水平的划分,结合“概率与统计”的学习内容,构建了数据分析素养观下的“概率与统计”高考试题三维分析框架(图1).
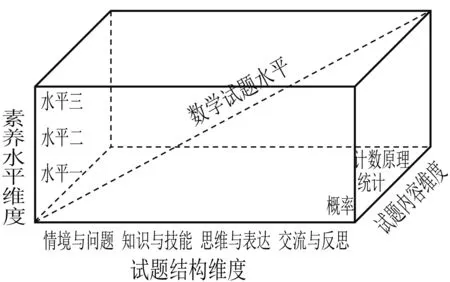
图1 数据分析素养观下的“概率与统计”高考试题三维分析框架
首先是试题结构维度.依据学业质量水平,分为情境与问题、知识与技能、思维与过程和交流与反思四个方面.其次是试题内容维度.依据课程标准的内容要求,分为概率(包括必修课程:随机事件的概率、随机事件的独立性;选择性必修:随机事件的条件概率、离散型随机变量及其分布列、正态分布)、统计(包括必修课程:获取数据的基本途径及相关概念、抽样、统计图表、用样本估计总体;选择性必修:成对数据的统计相关性、一元线性回归模型、2×2列联表)、计数原理(排列与组合、二项式定理),最后是素养水平维度,依据课程标准对数据分析素养水平划分,分为三个水平.
3 2017-2019年“概率与统计”试题分析
全国卷由国家教育部考试中心命题,使用范围广,影响力大,备受关注.先对2017-2019年高考理科数学全国卷两年的相关试题进行编号、分类,试题指的是和概率与统计内容相关的试题,本文以2017-2019三年的全国卷(Ⅰ,Ⅱ,Ⅲ),共九套试卷中的“概率与统计”为例,利用分析框架进行分析.
3.1 “概率与统计”高考试题的整体分析
从表2可以看出,“概率与统计”的内容知识基本是以1道客观题(5分)加上1道解答题(12分)的固定模式去进行考查.2017-2018年无论在题型还是分值等方面都很稳定.2019年,“概率与统计”的题目数量、分值均有所增加,这说明“概率与统计”在高考中将越来越受到重视.
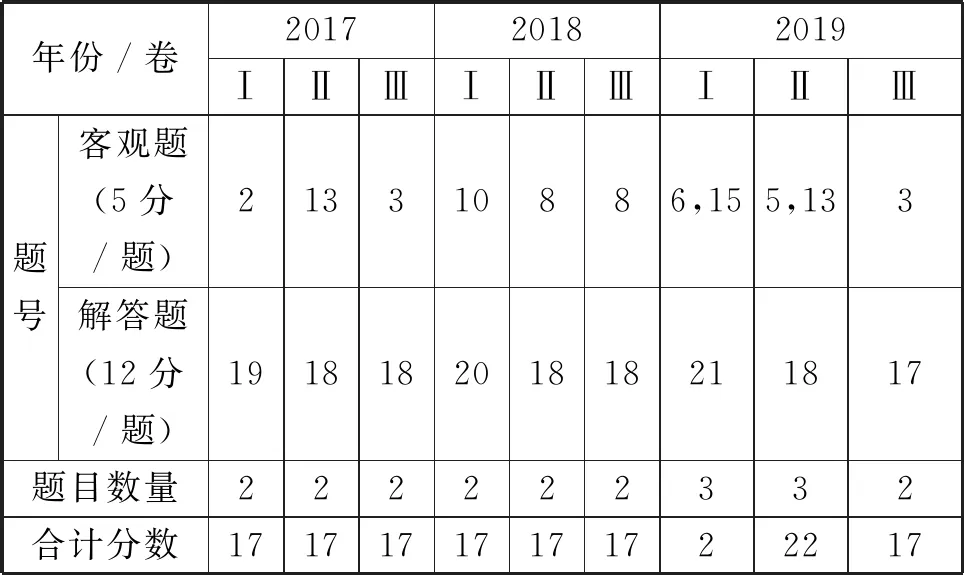
表2 2017-2019年“概率与统计”试题分布情况
3.2 试题结构维度分析
在高考试题中,选择合适的问题情是考察数学学科核心素养的重要载体.因此,本部分主要分析“情境与问题”方面.
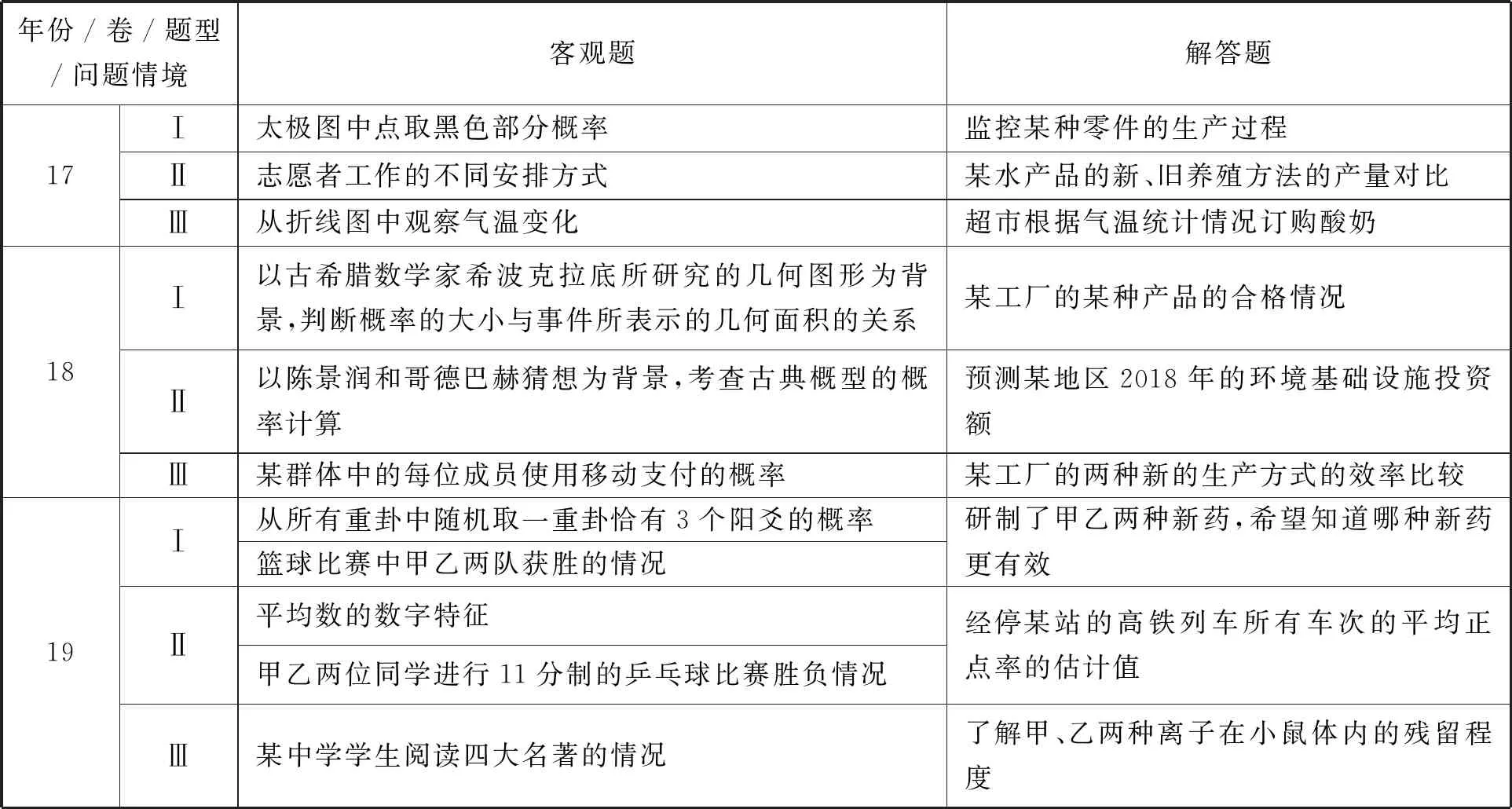
表3 2017-2019年高考理科数学全国卷问题与情景考查状况分布
由表3可见,近三年情境主要包括现实情境、数学情境、科学情景、其他情景.图2是2017-2019年高考理科数学全国卷“概率与统计”试题的情境分布情况,近三年的三套卷“概率与统计”试题都有现实情境的,共有15道题目,每种情境可分为熟悉的、关联的、综合的,数学问题是指在情境中提出的问题,从学生认识的角度分为:简单问题、较复杂问题、复杂问题.这些层次是构成数据分析素养划分的基础,也是数据分析素养评价等级划分的基础.图3表明这3年试题的问题情境大致以现实情境为主,占统计总数的75%.
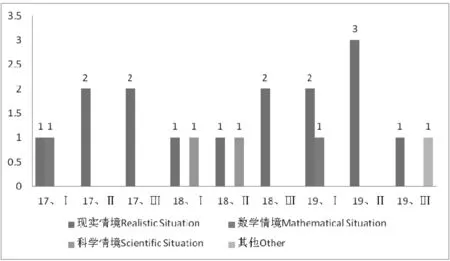
图2 2017-2019年“概率与统计”试题的情境类型
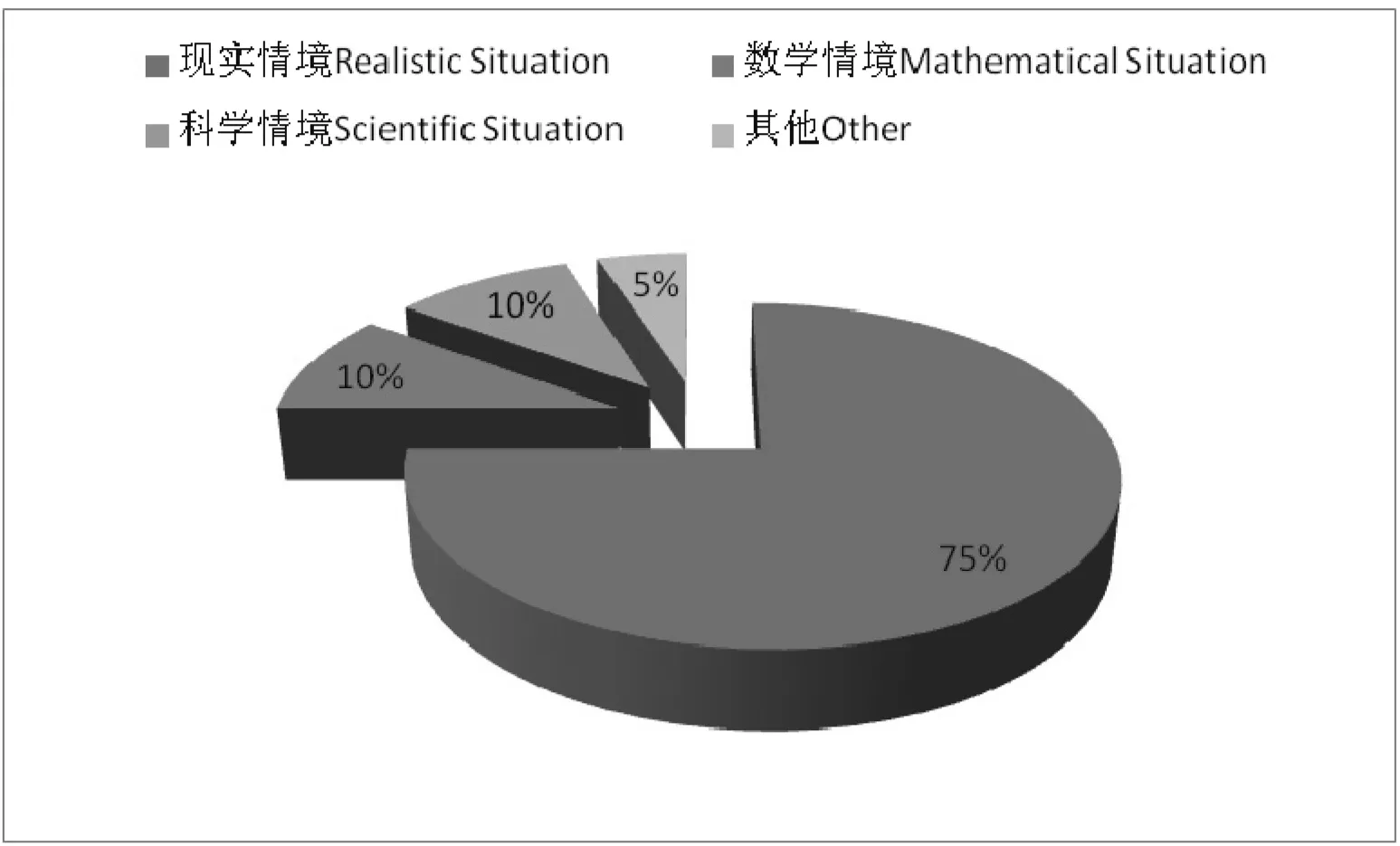
图3 2017-2019年“概率与统计”试题的情境分布
问题情境可分为熟悉的、关联的、综合的.由表4可见,2017-2019年全国卷理科“概率与统计”高考题共有20道题目,其中10道题目的问题情境属于综合的,占统计总数的50%.
3.3 试题内容维度分析
《普通高中数学课程标准(2017年版)》指出高考命题中需要突出内容主线和反应数学本质的核心概念、主要理论、通性通法、数学应用和实际应用.表5统计了考查内容的具体情况.
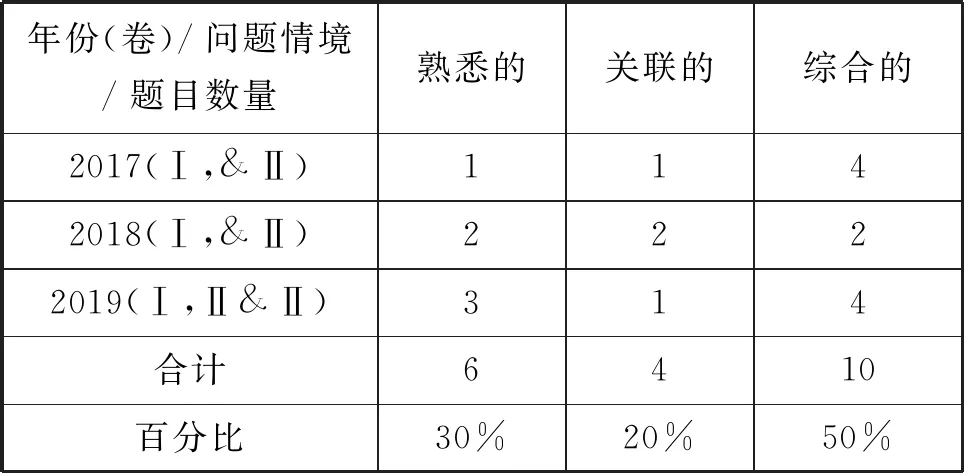
表4 2017-2019年“概率与统计”试题的情境难度
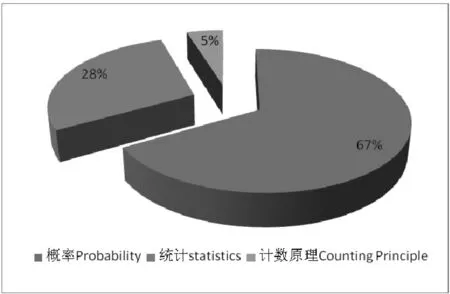
图4 2017-2019年概率与统计考查内容分布情况
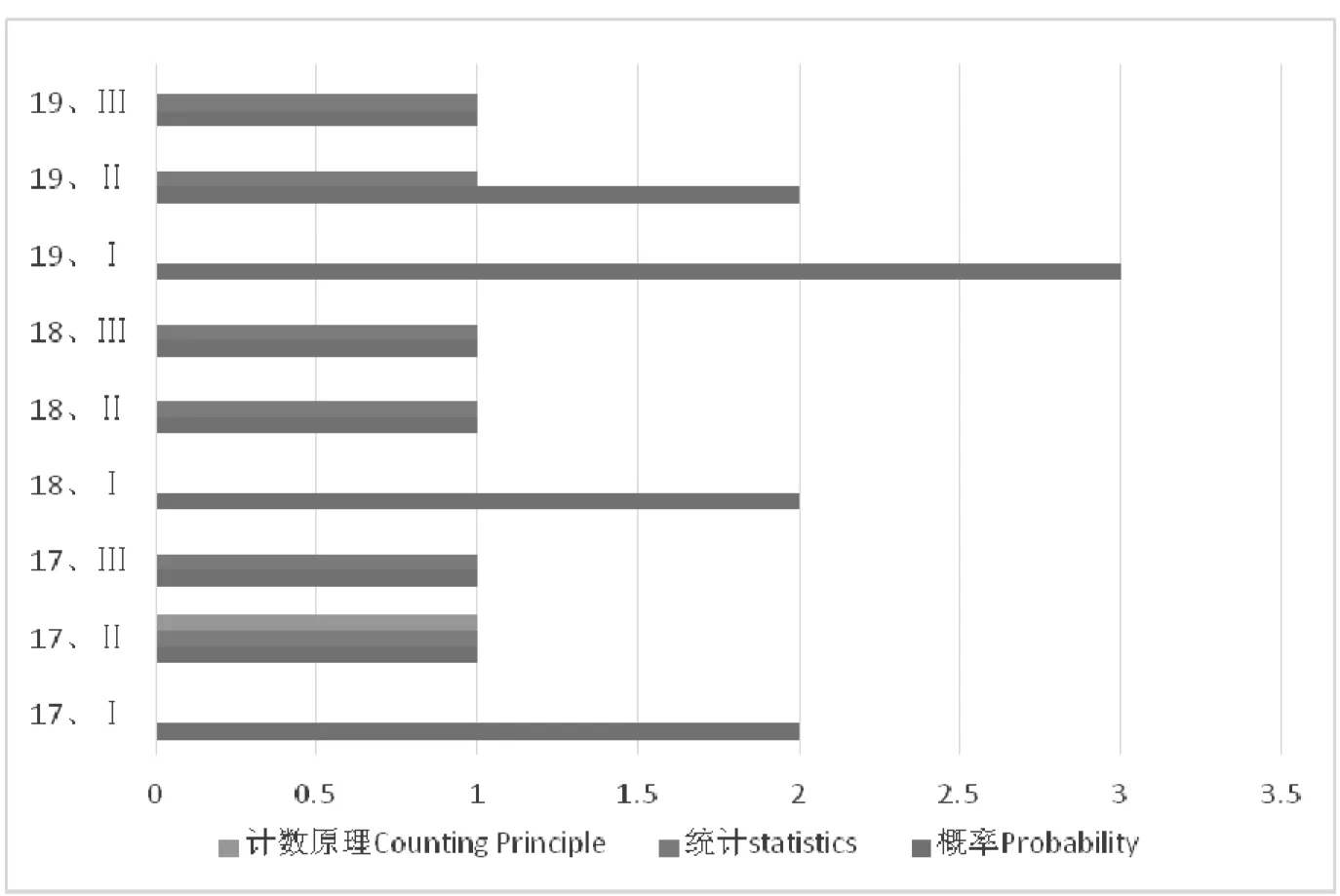
图5 2017-2019年概率与统计考查内容试题分布情况
图4是近三年试题内容的分布情况.其中,概率内容(随机事件的概率、随机事件的独立性、随机事件的条件概率、离散型随机变量及其分布列、正态分布)是主要考察内容,其次是统计内容,计数原理最少,只有2017年1道题考察过,仅占4%(图5).
3.4 素养水平维度的分析
近三年的11道客观题的考查基本处于“数据分析”的水平一;近三年的9道解答题的考查则基本处于“数据分析”的水平二.故整体而言,近三年高考试卷关于“概率与统计”的命题难度基本可以达到“数据分析”的水平二.而之所以说是“基本”,则是因为从知识与技能方面去看,上述的解答题可以说达到了“水平二”状态,但从客观题和解答题这两种题型的解题情况,无法确定学生是否在思维与表达这个方面上同样达到“数据分析”的水平二.这需要继续分析学生的答题情况.
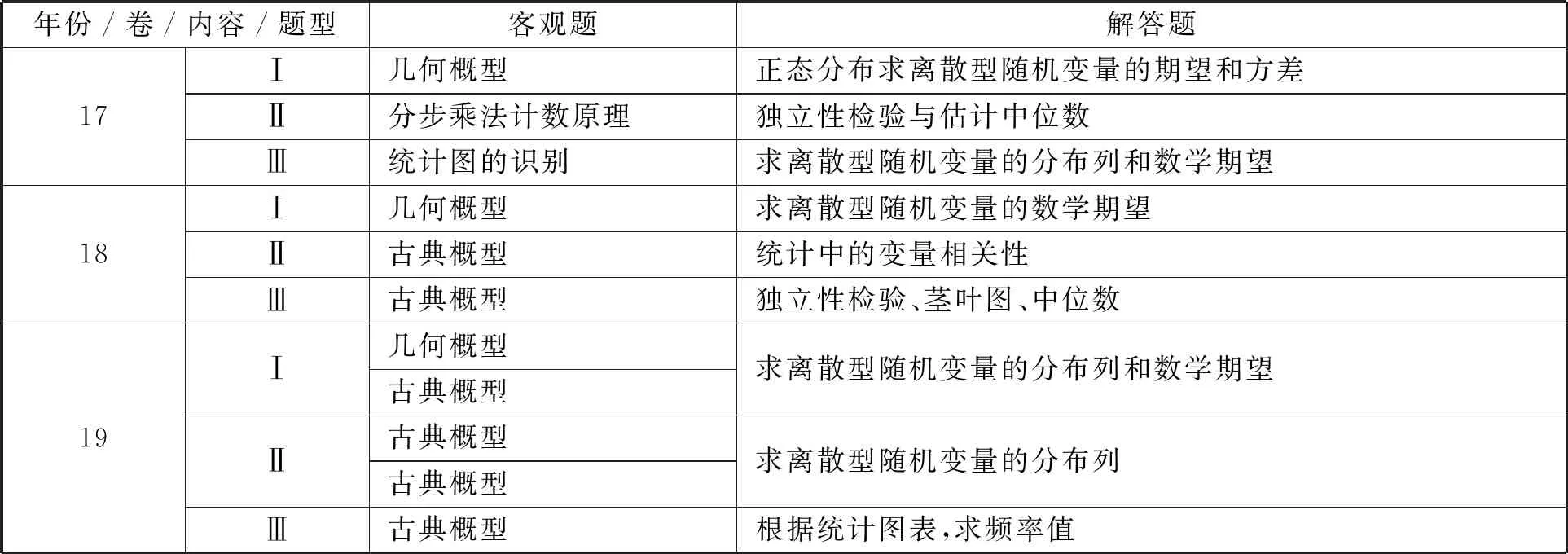
表6 2017-2019概率与统计考查内容基本情况
4 结论与建议
4.1 结论
基于数据分析素养观下的高考试题分析框架,对2017-2019年高考理科数学全国卷“概率与统计”试题进行了纵向分析,结果表明:(1)近三年,特别是2018-2019年,试题均较好地反映了数据分析素养,且客观题基本上处于水平一,解答题处于水平二;(2)试题情境设置灵活,更侧重生活情景,学生熟悉情境较多,解答题主要是综合的;(3)试题知识考查面全,重点突出,在考査概率知识的同时,注重渗透统计推断思想;(4)试题越来越强化数学应用和数学文化方面的考查力度,重视数据分析素养,充分体现“概率与统计”知识在生活中的应用;(5)试题越来越重视学生的数学建模能力和数学探究能力的考查.
4.2 建议
(1)注重数据分析素养的考查,适当降低计算量、计算复杂度
关于“概率与统计”内容的试题设置要注重让学生认识到确定性数学和不确定性数学之间的差异,理解并接受不确定性思维,并懂得运用统计思想和概率模型思想去解决问题.也就是说命题应侧重让学生了解统计方法的基本思想及其应用[4].新课标提出通过四个方面去综合评价学生“数据分析”核心素养水平,实质就是降低计算量、计算难度,避免学生单纯记忆和机械套用公式进行计算,是进一步对学生在思维与表达、交流与反思等方面提出具体的要求,这就要求试题设置要考察学生是否很好地理解了不确定性思维并初步运用其相关思想去解决问题.对于每一道试题,命题人除了要给出传统的评分标准外,还需要给出反映相关数学学科核心素养的水平划分依据.综合上述分析,试题设置应注重数据分析素养的考查,适当降低计算量、计算复杂度.
(2)设置开放题,综合考查“数据分析”素养
在上述对于解答题的分析当中,我们只能根据学生的解题情况去判断知识与技能这个方面上的水平,难以确定学生是否运用了相应水平的思维去解题,而上述也得到:未来的高考命题很有可能会从多个维度去综合考查学生的学业质量水平.因此建议,设置合理的开放题,可以从答题情况和答题理由中观察学生的思维和表达过程,显然这种类型的命题形式可以从多个维度上综合反映学生“数据分析”核心素养的水平,故认为未来的高考命题可能会出现这类型题目.但由于开放题是遵循满意原则和加分原则进行评分(达到测试的基本要求视为满意,有所拓展或创新可以根据实际情况进行加分),由于这种评分方式往往会带来评分的公平性问题,故命题时往往要考虑这类题目阅卷的公平性和可操作性.
(3)设置综合题,对不同数学学科核心素养的综合考查
前面提到未来的高考命题会趋向于从多个方面去综合考查学生的“数据分析”学科核心素养.而这里讲的不同数学学科核心素养的综合考查,则是指一道高考题目综合考查了不同的数学学科核心素养,其中不同数学学科核心素养是指新课标提出的六种数学学科核心素养.比如在一道估计总体性质的题目中,用样本空间的数字特征估计总体的数字特征或性质,是统计建模的基本思想和基本手法,既可以表现数据分析素养水平,也可以表现数学建模素养水平,像这道题目在考查了“数据分析”素养的同时,也考查了“数学建模”素养.未来的高考命题可以对不同数学学科核心素养进行综合考查.
