中国与加拿大初中数学教材中数学文化的比较研究
——以“勾股定理”内容为例
2020-12-03吴超萍马俊海浙江师范大学教师教育学院321004
吴超萍 马俊海 (浙江师范大学教师教育学院 321004)
自20世纪80年代以来,随着数学家、数学教育家等专家学者对数学文化的研究日益深入,数学和数学教育的社会文化属性已经越来越获得数学教育共同体的共识.例如,《义务教育课程标准(2011年版)》[1]指出:“数学文化作为教材的组成部分,应渗透在整套教材中.”教科书作为学校课堂中教与学的工具和媒介,是课程的“法定”文本,有目的地选择和传承一定价值取向的文化[2],对教科书的分析是研究课程编制水平的一种有效方式.加拿大教学质量一流,注重发展学生综合素养的培育,且教育体制与我国接近.以“勾股定理”内容为例,从文化视野分析中、加初中数学教材中数学文化的组织与编排,以期为我国数学教师批判性认识和使用教科书提供参考.
1 研究设计
本文选取使用范围广泛的、人民教育出版社出版的《义务教育教科书·数学》(八年级下册)(简称“人教版”)和加拿大MikeCzukar出版社的初中数学八年级教科书(简称“MMS版”)中“勾股定理”内容作为研究对象,主要分析两版数学教科书中“勾股定理”内容是如何被表征的,进而分析数学教科书中的数学文化.两版教材具体信息如表1所示.
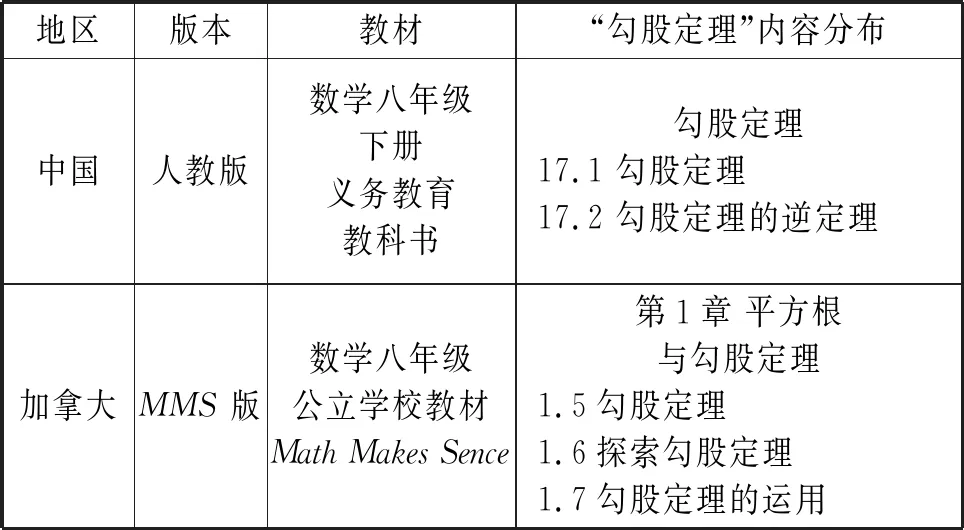
表1 两国教材基本信息
本研究在汪晓勤[3]等人研究的基础上,从数学文化的栏目分布、内容类型、运用水平三个维度加以分析.其中,栏目分布划分为非正文、引入、例题和习题,内容类型分为数学史、数学与生活、数学与科学和数学与艺术,数学史的运用水平按数学史与数学知识的关联程度的高低分为点缀式、附加式、复制式、顺应式和重构式,其余类型的数学文化运用水平分为外在型、可分离型和不可分离型.
研究进一步对数学文化的运用水平进行量化,对数学史的五种运用水平(分别记为A1,A2,A3,A4,A5)从低到高分别赋值1~5,并采用函数H1表征数学史运用水平
对其余类型数学文化的三种运用水平:外在型(B1)、可分离型(B2)、不可分离型(B3)分别赋值1~3,采用如下函数H2表征数学史运用水平
2 “勾股定理”中数学文化内容的比较分析
根据分析维度,对我国人教版和加拿大MMS版数学教科书中“勾股定理”中的数学文化内容进行统计分析,相关结果如下.
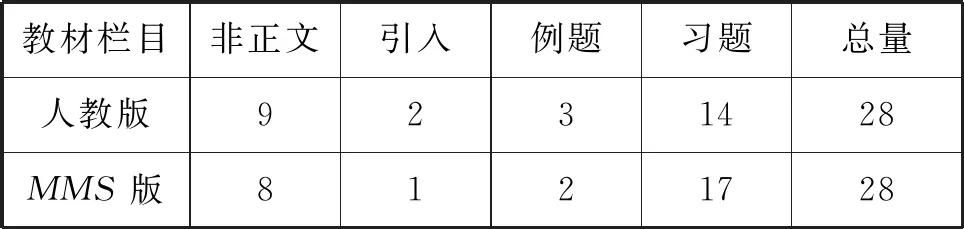
表2 两版“勾股定理”中数学文化的栏目分布
栏目分布数量上,两版教科书中数学文化内容相当丰富,多达28处.在各个栏目中分布数量相当,习题栏目占比最多,详见表2.在数学教育传统上,常把数学视为解题的活动,以及“孰能生巧”等传统文化观念的影响,教科书中习题的数量一向占比最多,同时,数学教学中以问题引领和问题驱动,习题中数学文化数量之多也表明数学文化为数学问题提供了一定的社会文化背景.进一步运用SPSS对两版“勾股定理”中数学文化在不同栏目的数量进行差异性分析,从卡方检验P值(P=0.830>0.05)可知,两种教材在数学文化栏目分布上无显著性差异.但从各部分的均衡性来看,人教版分布相对更佳.
在内容类型上,两版教材“勾股定理”中的数学文化丰富集中,分布不均匀,详见表3.其中,人教版在数学史方面数量多于MMS版,在数学与生活上,MMS版多于人教版,共出现了18处,两版教材在数学与科学、数学与艺术上均涉及较少.进一步运用SPSS对两版“勾股定理”中数学文化在内容类型的数量进行差异性分析,从卡方检验P值(P=0.029<0.05)可知,两种教材在数学文化类型上有明显的差异.以下分别对数学史、数学与生活、数学与科学、数学与艺术进行详细分析.
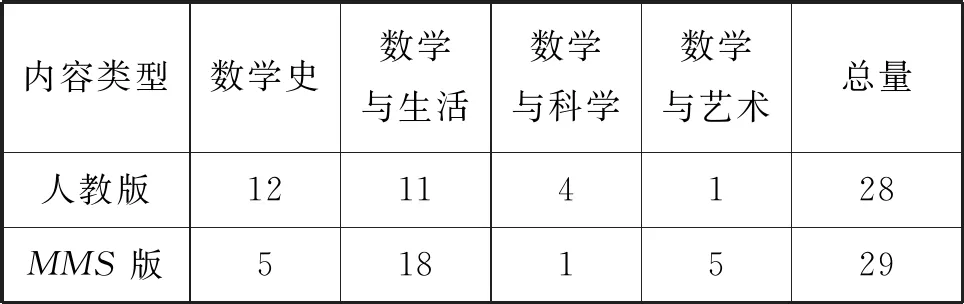
表3 两版“勾股定理”中数学文化的内容类型分布
在数学史上,人教版中“勾股定理”中显性数学史和隐性数学史分别占比58.3%和41.7%,MMS版中显性数学史和隐形数学史分别占比60.0%和40.0%.通过SPSS进行卡方检验,从P值(P=0.949>0.05)可知,两版教材在数学文化之数学史无显著性差异.人教版和MMS版都对数学史的应用采用显性与隐性相结合的方式,显性与隐性之间大约6∶4.显性数学史出现的方式集中在章头、阅读材料等栏目中,例如“介绍毕达哥拉斯、费马、怀尔斯等数学家生平,展示数学家的肖像等;隐性数学史出现的方式集中在例题和习题中,例如改编中国古代《周髀算经》和《九章算术》中记载的数学题.
在数学与生活上,人教版中“勾股定理”中个人生活和公共生活分别占比54.5%和45.5%,MMS版中个人生活和公共生活分别占比55.6%和44.4%.通过SPSS进行卡方检验,从卡方检验P值(P=0.958>0.05)可知,两种教材在数学文化之数学与生活无显著性差异.两版均涉及个人生活与公共生活,相对均衡.例如,人教版中个人生活包括“测量学校旗杆高度”“学生走路上学距离问题”等,公共生活包括计算“港口方向和距离”等.MMS版中的数学与生活内容总量略高于人教版,教材中列举了系列诸如“放风筝”“棒球场”“学生制作物品”等与学生个人生活情境有关的实例,在公共生活上融入了“坡道停铲雪机”等情景.
在数学与科学上,人教版中“勾股定理”中生命科学和物质科学分别占比25.0%和75.0%,MMS版中都为物质科学.通过SPSS进行卡方检验发现,两版教材在数学与科学类型上无显著性差异.两版教材涉及科学部分都较少,人教版主要涉及生命科学和物质科学;MMS版主要只涉及物质科学.这表明在“勾股定理”的教材编排中,与生物、化学、政治等多学科知识与内容相结合有待加强.
在数学与艺术上,人教版中“勾股定理”中都为人文内容(100%),MMS版中人文与美术分别占比40.0%和60.0%,通过SPSS进行卡方检验发现,从卡方检验P值(P=0.273>0.05)可知,两版教材在数学与艺术类型上无显著性差异.两版教材涉及数学与艺术的数量较少,MMS版在数量上相对较多,例如在人文方面融入了原住民所带的帽子和被子图案;在美术方面融入了图标的涉及、画框的制作等,这与加拿大对艺术教育的重视有关,我国在数学与艺术方面也应适当加强重视.
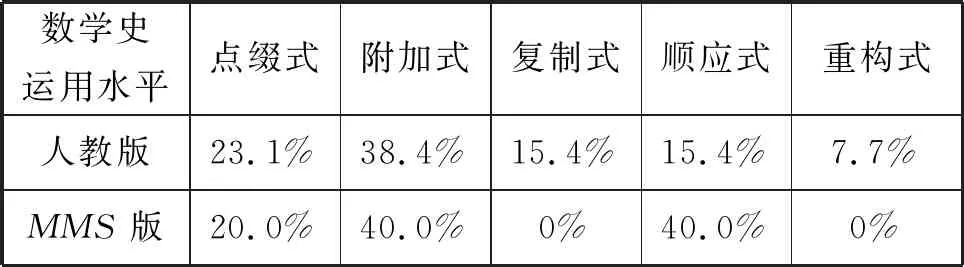
表4 两版“勾股定理”中数学史的运用水平分布
在数学文化运用水平上,人教版“勾股定理”中数学史运用水平比MMS版更为丰富,详见表4.人教版中数学史的各运用水平均有涉及.进一步聚焦到每类运用水平可知,两版教材在点缀式和附加式占比相当且较大.在顺应式上,人教版中将《九章算术》中水池和芦高问题进行改编重新呈现,MMS版和人教版都将特奥多鲁斯螺旋进行改编重现,丰富了学生对数学史的了解.利用数学史运用水平计算公式可得人教版数学史运用水平得分为2.5,MMS版得分为3.2.总体而言,人教版在数学史方面分布和数量占优,在运用水平方面,MMS运用水平更高一些,换言之,教材中数学史的数量与数学史运用水平并无直接关联.
在其余文化运用水平上,两版教材在本章中均未出现“外在型”运用水平,数学文化的运用水平相对较高,且二者在内在型分类占比上差别不大,有30%左右的题目属于不可分离型,如人教版中“零件两孔距离”“木杆折断”“两人不同方向行走距离”等情境;MMS版中“飞机落地”“铺地板”“制作画框”等情境,这些内容的加入有利于将数学问题和生活中真实情境加以联系.在可分离型上,两版教材占比都超过了70%,原因可能是在数学与生活的分类上,出现了较多可以分离的应用情境.通过计算得到人教版其他数学文化运用水平得分为1.25,MMS版其他数学文化运用水平得分为1.27,说明MMS版在其他数学运用水平上略高于人教版.总体而言,两版教材都需要进一步提高对生活素材的运用水平,使之让数学文化与数学知识的关联程度更高.
3 结论与建议
基于上述分析结果,给出以下结论和建议.
(1)均衡教科书中数学文化栏目分布
中加在数学文化栏目分布上呈现相似性,主要都集中在习题部分,而非正文,引入和例题部分较少.事实上,分布于不同栏目的数学文化都有其存在的不同意义.非正文的数学文化能够引导学生进入数学知识的学习,提升数学兴趣;引入部分是教师开展教学很好的素材,起到铺垫作用;例题和习题部分的数学文化多与生活息息相关,并且融入历史、天文、地理等,让数学知识真正来源于生活并服务于生活.因此,在教材的编写上要合理分配各栏目数量,不局限在某一栏目中,让学生从不从角度感受数学文化的价值与力量.
(2)呈现多样数学文化类型
从整体上看,虽然两版教材都对数学史、数学与生活、数学与科学、数学与人文艺术等内容进行了关注,涉及领域广,但通过卡方检验可知,中加两版教材在数学文化类型上差异性显著,原因在于人教版在融入数学史的总量上明显高于MMS版,MMS版则更加侧重数学与生活的呈现.聚焦于特定类型进行细分,人教版和MMS版在数学史类型上更多停留在显性数学史,在数学与生活类型上占比相当,而在科学和艺术方面都有所空缺,呈现出分布不均匀的现象.因此,教材编写时应呈现多样的数学文化类型,在数学与科学方面可以融入计算机、统计学等运用于操作;在数学与艺术方面可以融入民族数学文化、影视作品中出现的相关数学知识,不仅能够丰富教材的编写内容,也能够开阔学生的视野,提高创新能力和实践能力.
(3)提升数学文化运用水平
当前中学教学普遍存在“高评价、低应用”的现象,很重要的一个原因在于对教材中数学文化的运用水平不高.从上述分析也可知,人教版在数学史的总量上明显多于MMS版,但在计算运用水平时发现MMS版运用水平高于人教版,即运用水平的高低不止是数量上的取胜,更要在质量上过关.如果教材中的数学史的呈现多停留在点缀式、附加式等方式上,其他数学文化类型多停留在外在型、可分离型上,那么就无法真正将数学文化融入数学学习中,也就无法真正促进数学文化的发展.因此,教材中应采用更高水平的数学文化运用方式,数学史融入采用顺应式和重构式;其他数学文化方式向不可分离型转变,从而改善“高评价,低应用”的问题,让数学文化自然而又有内涵地与数学问题结成一个统一的有机体.借助数学文化进行数学问题的解答、判断与学习,让学生形成数学意识,真正让数学文化发挥作用.
