数学解题中“会而不对”的现象分析与对策研究
2020-12-03江苏省无锡市第一中学214031
钱 铭 (江苏省无锡市第一中学 214031)
朱福进 (江苏省无锡市辅仁高级中学 214123)
1 问题提出
作为一名数学教师,我们常常会碰到这样一种奇怪的现象:许多学生对一些题目感觉会做,也能下笔求解,但就是不能得出正确的答案,在做作业与考试时自己浑然不知,满以为是对的,等到与别人交流或老师讲评时才恍然大悟,这就是所谓的“会而不对”的现象.有些教师将学生解题时出现的“会而不对”的现象称之为“低级错误”,不少学生则将其归咎为“粗心大意”或“一时疏忽”,都误以为只要在解题时细心一些就可以避免.然而,在后续的作业和考试中,这种“会而不对”的现象仍然频频出现,成为阻碍学生进步的一个难以治愈的“顽疾”,不仅极大地影响了学生的学习成绩,也严重地挫伤了学生学习的积极性,制约了数学教学质量的提高和学生的长效发展,既困惑着学生,也困惑着老师.[1]那么,在数学学习中,学生解题“会而不对”的主要现象有哪些?产生这种现象的深层原因究竟是什么?在我们的数学教学中怎样才能有效地予以解决?下面结合笔者的教学实践作一些探索和研究,与同行交流,供大家参考.
2 现象分析
学生在数学解题中出现的“会而不对”的现象形式是多种多样的,其中的“会”是指有了解题思路,基本拟定了解题计划,“不对”是指解题的过程中出现了问题,或不能正确运用概念、定理、公式和性质,或不能合理地进行转化,或运算不过关造成差错,或书写过程丢三拉四、漏洞百出等等.结合“会而不对”的表现形式和产生的原因分析,常见的情形有以下几种.
2.1 概念模糊、似懂非懂导致会而不对
从知识层面看,不少学生因课堂上没有专心听讲或基础知识薄弱、悟性不够,或由于教学进度太快,留给学生思考、消化、理解的时间过少,导致他们对基本概念和基础知识表面上像是懂了,甚至还可以复述出来,但对其本质、内涵与外延并未真正地理解,其实不是真懂,而是似懂非懂,解题时只能机械地模仿,无法灵活和准确地加以运用,面对具体问题看起来会,做起来错,造成遗憾.
案例1已知点F1(-4, 0)和F2(4,0),平面上的一动点P满足PF1-PF2=6,试求动点P的轨迹方程.
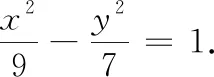
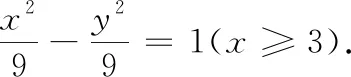
学生所犯的错误,根本原因在于对双曲线定义的理解似懂非懂,只是形式上、断章取义地记住了双曲线的定义,是浅层次的懂,没有能全面地把握双曲线定义的本质,对其内涵和外延缺乏足够的认识和了解,这样解题,会而不对就难以避免了.
2.2 审题偏差、遗漏条件导致会而不对
审好题是解好题的前提和关键,只有审好题才能解好题,稍有疏忽,便会“差之毫厘,谬以千里”.不少学生解题时急于求成,盲目自信,对审题重视不够,拿到题目匆匆忙忙地浏览一遍就仓促动笔,以致于题目的条件没有看清,要求没有吃透,甚至对已知条件有那些、解题目标是什么都没有弄明白,至于如何从题目中挖掘隐含条件、寻找内在联系、启发解题思路就更无从谈起,不可避免地要产生偏差,导致“会而不对”.
案例2抽样统计甲、乙两位射击运动员的五次训练成绩(单位:环),结果如下:

运动员第1次第2次第3次第4次第5次甲8791908993乙8990918892
则成绩较为稳定(方差较小)那位运动员的成绩的方差为.
这是2013年江苏高考第5题,是一道容易题,学过这一内容的学生应该都会做.在教学抽样统计时,笔者将这道试题给学生练习,许多人的解答如下:
易知甲、乙两人的均值都是90.
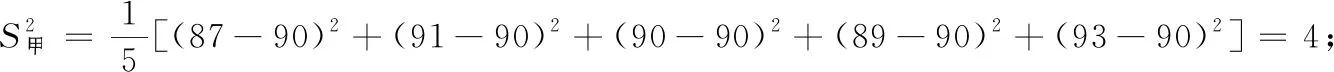

所以乙的方差较小,成绩较稳定的那位运动员是乙,故答案为乙.
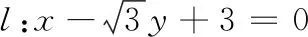
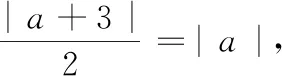
2.3 分类不全、顾此失彼导致会而不对
主要表现在运用分类讨论的思想方法解决问题时,所运用的知识和大体思路是正确的,运算和书写也不存在问题,但思维过程不严谨,对问题的思考不深入,对各种情况的分类不全面,忽略了对一些特殊情况或某些具体细节的讨论,忘记了数学概念、公式、法则和定理在具体运用时的限制条件,导致逻辑上的欠缺,致使“会而不对”,产生以偏概全、丢三拉四、顾此失彼的错误.
案例3过点A(2,3)作直线l,使得点B(-1,6)和点C(4,5)到直线l的距离相等,试求出直线l的方程.
许多学生的解法如下:
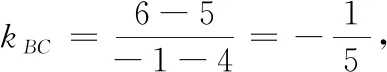
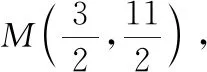
2.4 盲目变形、忽视等价导致会而不对
著名的数学家、莫斯科大学教授C.A.雅洁卡娅曾在一次向数学奥林匹克参赛者发表《什么叫解题》的演讲时提出:“解题就是把要解题转化为已经解过的题.”数学的解题过程,就是从未知向已知、从复杂到简单的不断进行化归转换过程,许多情况下,也是一个寻找充要条件的过程.若转化恰当,问题往往能迅速获解,若盲目变形,忽略转化过程中的等价性,则自然会导致做错题的现象发生.
案例4已知数列{an}是递增数列,且an=n2+bn+2(n∈N*),求实数b的取值范围.
我们常会见到如下的错误解法:


一般地,“y=f(n)(n∈N*)为增函数”是“函数y=f(x)(x∈R*)在区间[1,+∞)上是增函数”的必要不充分条件.本案例中所用的基础知识(数列、递增数列、二次函数、函数的单调性等概念)学生都“懂”,求解的思路也很难清楚,但因“数列递增”转化为“连续函数递增”时,进行了不等价转化,故而致错.
2.5 书写马虎、计算出错导致会而不对
数学习题的解决在绝大多数的情况下都是离不开运算的,在解题的过程中,即使思路和方法都正确,但书写马虎,运算不过关,不注意计算细节的处理,例如算理混淆、算法不优、过程繁琐、誊写失误,由上一步到下一步,把加号写成减号、把3写成5、把加减看成乘除、括号前是负号的情况下去括号时括号里的有些项不变号等,也会形成计算上的错误,导致会而不对.

这是一道高三理科数学模拟试题,难度不大,但做错的学生不少,一种比较典型的错误解法如下:
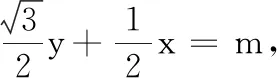
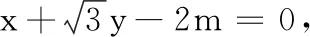
3 对策研究
课堂教学是一个师生的双边活动过程,教师是外因,是变化的条件,学生是内因,是变化的根据.导致学生在解题中出现会而不对的现象,其原因是多方面的,有学生学的因素,也有教师教学中教的问题.在我们的教学中,作为教师,需要从哪里入手,在何处着力,才能有效地帮助学生克服和解决会而不对的问题呢?
3.1 突出概念教学,建构深度理解,解决“似懂非懂”的问题
“数学根本上是玩概念的,不是玩技巧,技巧不足道也.”概念是反映事物特性或本质的一种思维形式,是构成数学知识、进行判断和推理的基础,数学的建构完全依赖于一个个明确的概念,没有数学概念就没有系统的数学思维,正确地理解数学概念是掌握数学知识的前提.数学概念是培养数学技能的沃土,对数学概念的深刻理解可以促进学生以此为生长点探索数学技能,而数学技能的操作又可以反过来加深对数学概念的认识,为更高层次的生长提供可能.因此,强化学生数学技能的一个重要对策,就是加强学生对数学基础知识的认识和理解,指导学生多动手实践,多练习基本技能,学会从不同角度思考问题,学会运用多种方法解决问题,在一题多解和变式训练中深化认识,建构理解.章建跃博士曾经说过:“要让学生养成‘回到概念去’思考和解决问题的习惯.”抓住了概念也就从本质上抓住了解决问题的关键,对数学概念理解越深刻,解题就越简洁越流畅.[2]因此,在进行概念教学时,教师要不惜时、不惜力,让学生充分经历概念发生和发展的过程,深刻揭示概念的本质,深入挖掘概念的内涵和外延,帮助学生建构起自己对概念的正确认识和深层理解,从而提高学生分析问题和解决问题的能力,提升学生的核心素养,促进学生有效地破解数学解题中由于似懂非懂而造成的会而不对的问题.
3.2 加强学法指导,养成良好习惯,解决“审题偏差”的问题
有一句名言:“学习数学意味着什么?那就是解题.”但笔者以为,学生学习数学的主要任务并不只是解题,更重要的是学解题,教师教的重点和学生学习的重点不在于解而在于学解,数学教学要注意加强学法指导,让学生学会学习、学会解题,帮助学生养成良好的习惯.美国著名的数学家G· 玻利亚在《怎样解题》一书中总结出科学的解题步骤:明确题意、制定计划、执行计划、总结解题过程.[3]在解题中,任何一个环节的错误都可能导致会而不对现象的发生.认真细致地审清题意、真正意义上吃透题意是解好题的第一步,若审题出错,则满盘皆输.怎样审准题,确保自己对题目的理解与题目本身的含义完全一致,这是教学中必须加强训练、着力解决的问题.教师在平时的教学中要注意帮助学生养成“用心、耐心、细心”的周密思考的好习惯.例如可以教会学生,在读题时要把关键的部分画出来,从心理学的角度来分析这个过程,圈出关键词的过程同时具有动作和视觉的输入,两种信息的同时输入,可以加深对题目中重要信息的短时间记忆.对于有些学生在解题的过程中书写潦草、缺乏依据、遗漏条件等问题,要引导学生注意换行、对齐书写、回代检验.学生如果能够养成良好的学习习惯,就可以有效地避免数学解题中由于审题偏差而导致的会而不对的问题.
3.3 注重解题回顾,提升反思能力,解决“顾此失彼”的问题
G·玻利亚认为:数学问题的解决仅仅只是一半,更重要的是解题后的回顾.罗增儒教授也曾经说过:“检验解题过程也是提升解题能力、积累解题经验、锻炼数学思维的一个重要途径.”[4]学生的错误和思维的优化是一个自我否定的过程,即以自我反思为前提.所谓“反思”,就是引导学生解题后再思考,对解难题过程中思维的受阻点及出现的原因进行分析.题目做过以后,应习惯性地回过头来望一望、想一想,题目的条件是否用全?方法是否正确?计算有没有出错?是否做到了每步都有理有据?还有其他解法吗?各种解法之间有什么区别?哪种解法最优?等等.通过回顾,整理出整个问题的经历过程,做到层次分明,以达到画龙点晴的目的.学生在检查中往往会受思维定势的影响,难以发现自已解题中的问题,这时教师应注意加强指导,例如指导学生换一种方法试一试,借助另一种思路来验证自己的答案是否正确,也可以应用逆向运算法来验证答案,来查出遗漏的部分,避免错误的发生.在平时的教学中,教师要善于引导学生反思探究,探寻知识与方法之间的联系,发现条件与结论之间的差异,提升对问题本质的认识,让学生在不断的联系和整合中,丰富和完善认知结构,站在系统的高度理解数学,构建更广泛、更有效的解题经验,破解数学解题中因分类不全、顾此失彼等原因造成的会而不对的问题.
3.4 渗透化归思想,优化思维品质,解决“忽视等价”的问题
数学问题的解决过程,实质上是一种思维活动的化归和转化过程.所谓化归和转化,就是在分析解决问题时,把那些待解决或难解决的问题,通过有意识的“联想—转化”,由未知向已知化归,把不熟悉的、不规范的、复杂的问题化归为熟悉的、规范的甚至模式化的、简单的问题,从而求得原问题的解.化归与转化是分析问题和解决问题的重要思维模式,是数学解题的必经之路.化归和转化包括等价转化和非等价转化两种.等价转化要求转化过程中前因后果是互相逆推的,是充分必要的,它能保证转化后得到的结果仍为原问题的结果;非等价转化其过程是充分或必要的,所得到的结果不一定是原问题的结果,要对结论进行必要的检验和修正.许多学生在解题的化归转化过程中,不能区分等价转化与非等价转化,常常将不等价的转化过程误以为是等价转化的过程,而产生解题错误.因此,在教学的过程中,一定要高度重视化归转化思想的渗透,帮助学生明确化归转化的等价性与非等价性的不同要求,在实施化归转化时确保其等价性,保证逻辑上的正确,如果出现不等价转化,一定要附加约束条件,或注意回过头来进行解题检验.要注意让学生学会从多角度考虑问题,形成科学的思维习惯,掌握正确的思维方法,使学生的思维品质得到优化,思维能力得到提升,从而有效地破解由于忽视等价而形成的会而不对的问题.
3.5 强化运算训练,培养运算能力,解决“计算出错”的问题
运算能力是一种集算理、算法、计算、推理、转化等多种思想、方法于一体的综合性能力,解决数学问题,不仅要能正确地运用数学的知识、思想和方法,也离不开计算方面的技能和技巧.准确是运算的基本要求,运算的准确性来自对知识的正确理解和掌握,只有切实掌握有关知识,才能使运算明确方向,为运算提供可靠的依据.运算不准确在很大程度上是由于对基本概念理解不深,对基本公式、法则掌握不够透彻,以及对它们的运用不够熟练.这就要求我们在教学时把概念、定义、定理、公式等讲清楚,高度关注学生在运算中反映出来的知识上的缺漏,不要把解题错误的原因,简单地归结于粗心大意.运算能力还表现在对算理的理解和运用上,以及根据问题的条件寻找并设计合理、有效的运算途径,通过运算进行推理和探求.其中算法和算理是基础,基础不扎实,能力培养只能是空中楼阁.因此,必须指导学生在弄懂、弄通必要的算法和算理上下工夫.要着眼于细节的处理,引领学生通过反思抓住问题的本质求解,逐步使运算简洁合理.实践表明,提高运算能力是一项复杂的系统工程,是一项长期的任务,不可能一蹴而就.我们要珍惜每一次训练机会,有计划、有目标、有意识地进行长期的渗透和强化,使学生养成正确、合理、快速地进行运算的习惯,从而有效地破解由于计算出错导致的会而不对的问题.
总之,作为一名数学教师,要深入研究学生解题时出现会而不对现象的原因以及应对之策,改进教学,牢记细节决定成败,规范自己和学生的解题行为.在实施解题教学的过程中,要以提高数学素养、发展思维能力、培育理性精神为核心,重视概念教学和运算能力的培养,坚持以学生为主体,多角度、多途径地示范解题分析,充分地展示和暴露解题的思维与探究过程,挖掘背景知识,揭示问题本质,渗透数学思想方法,注重解后反思,及时归纳总结知识和方法,并不断地将其纳入已有的认知系统,使学生在掌握知识的过程中学会思考,帮助学生养成良好的解题习惯,积累更多的解题经验,加强学生对数学的理解,提高学生的数学能力,提升学生的核心素养,真正解决学生在数学解题中出现的各种会而不对的问题.
