每一道题目都是一个课程
——现象教学视角下的解题教学*
2020-12-03李宏铭江苏省苏州市吴江盛泽中学215226
李宏铭 (江苏省苏州市吴江盛泽中学 215226)
1 引言
案例1(全国一等奖课例)课题“一元二次方程的判别式”,有下面的一个细节:在讲完一元二次方程判别式的概念以后,教师给出了方程x2+12x+16=0,并说:“请同学们帮老师计算一下Δ,看它的符号是正还是负.”
在这里,教师向学生布置的是一个“计算”的任务,而不是理解和应用判别式的素材!学生没有对判别式的意义进行思考,没有将判别式和情境做联结.他们虽然在计算,却不知道为什么要计算,不知道计算以后要干什么.尽管最后教师揭示了“符号是正还是负”的实际意义(用来判断根的存在性),但是在活动之前和活动之中学生都没有对活动本身有整体认知和价值判断.不知道活动目的、没有对活动的意义作评估,学生的活动是机械的、被动的.不得不说,这样的任务布置已经脱离了本节课的教学主旨,把学生引到了无关的方向上去了.这样的课能被层层推荐到全国最高级别的比赛上并最终获得一等奖,说明当时数学教育界对这种做法是认同的.虽然这是十几年前的赛课,可以说代表的是十几年前的认识状况,现在我们的教学观念已经发生了很大的变化,但是此种做法仍然普遍存在,在杂志上把它当作经验来介绍的文章还有很多(见后文),这就是笔者要谈这个话题的缘由.
2 关于解题教学
解题教学可以说是数学课堂永恒的主题.怎样看待解题教学、怎样进行解题教学,可能永远都讨论不完(本文涉及的仅是其中很小一部分).
第一,如果把题目当作任务来布置,学生就成了执行者;如果再把任务分解成一道道的工序让学生去执行,学生就成了机器人.若换个角度,把题目当作一个现象,当作现实世界或数学世界中的客观存在,让学生去观察、分析、解构、整合,经历一阵大脑风暴后生成心理表征和语言表达,学生就成了一个探究者和发现者.后一过程就是一个动态的过程、生长的过程,是视野逐步打开和立足点逐渐提升的过程.
第二,教师讲题肯定不是从头到尾展示题目解法,而应该开启与学生互动的平台.教师需要找准学生需要辅助的地方,以确定讲课的目标、重点、难点,确定讲解方法.而所有这些都必须是结合学生活动才能确定,也只有在互动中才能收到实效.
第三,给学生讲的每一个题目都不应当仅仅是一个题目.对人类的发展而言,完全不需要学生去解决教材上的任何一个问题,因为它的答案已经被知晓.讲题是为了什么?为了使学生获得知识的增加、能力的增强和素养的提高,一句话,为了学生的生命成长.而这个使命显然不是单纯的一个题目所能承载的,更不是告诉他们一个答案就能奏效的.怎么办?
我们希望每一道题目都是一个课程,是教学活动得以实施的蓝本和载体,而不仅仅是布置下去的一个固定的任务.学生在与题目、与教师以及与同伴互动的过程中,可能发现预期的结论,也可能发现预期结论之外的东西,还可能演化出新的问题、新的现象,进而引发新一轮的互动……这就带来了无尽的可能性和无限的生长空间.若如此,创新与创造也就是水到渠成的事了.
3 把题目当作现象
教师讲的题和练习册上的题,有区别吗?有!前者有教师在场而后者没有.教师是教学的主导因素,如果教师在场和不在场时解题教学的形态没有变化,“主导作用”的发挥就无从谈起了.有教师在场,可以把题目处理成动态的、开放的、不完整的甚至是“错误”的,让学生在活动中完善它或者更正它,实现对本质和非本质、正面侧面和反面的完整认识,这些是练习册所不能做到的.练习册上的题只能是静态的、完整的,必须有明确具体的条件罗列和清晰无误的任务条目.
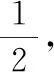
案例2求椭圆的标准方程.
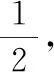
生:(活动)……好像不对.
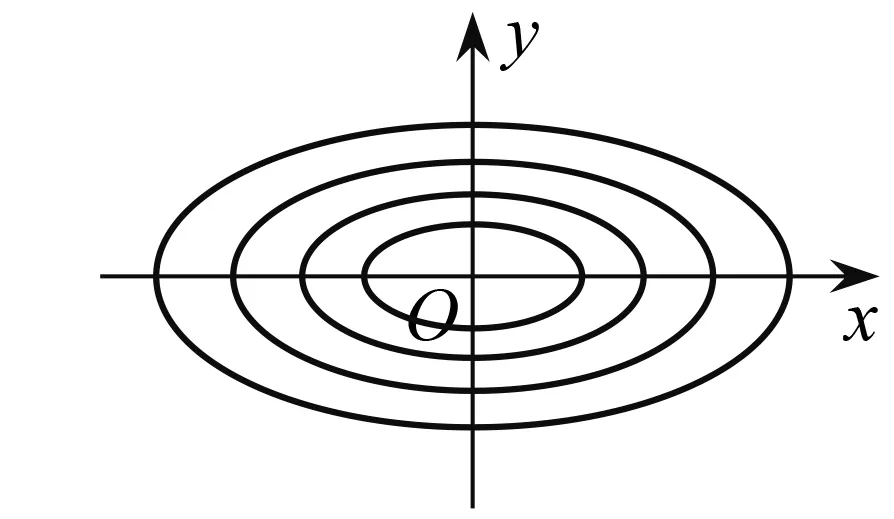
图1
生众:不对,这是个错题.
师:错题?不能求吗?
生:不能求.
师:知道离心率,难道不能把椭圆确定下来吗?
生:不能,只能确定椭圆的圆扁程度.
师:比如,这个题目中是什么样的椭圆?请画示意图.
(学生画出图1)
师:这样的椭圆有无穷多个.怎样才能确定一个?
生:需要加条件.
师:加几个条件?
生:只要一个就够了.
师:要一个什么条件?
生:可以加焦点坐标.
师:我们来试一下,加“一个焦点是(3, 0)”,求其标准方程.
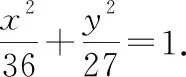
师:还可以加其他条件吗?
生:可以加长轴长、短轴长、焦距、准线方程……
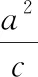
师:是的.下面我们出一个题看看.(师生合作出题)
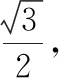
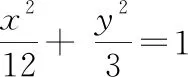
练习2:请你自己出一道求椭圆标准方程的题,与同桌交换做一下.并把你认为好的题目推荐给大家.
至此,学生已经领会到了求椭圆标准方程的基本方法.值得注意的是,这里解决了求椭圆标准方程的“所有”基本问题,却没有经过大量的解题训练,甚至没有把10种基本题型全做一遍(只做了3道题),这是与题海战术完全不同的学习形态.教师提供的不是一个题目,而是一个课程!学生从这里得到的不是对操作技能的总结,而是对数学思想的感悟.这个案例中学生感悟到的是方程思想,解几个未知数就需要几个方程.在遇到其他形式的题目或者在更复杂的情境里,学生也可以洞悉到问题的原型和本质,并用数学的普遍思想统领对问题的思考,比如去寻找两个基本条件、建立方程组并求解.这就相当于把所有的具体形态都忽略了,只剩下一个抽象形态的知识,而这个知识又是无所不包的,也许这就是我们的“道”吧.当学生把所有具体题目都忘掉(也必然会忘掉)以后还剩下的部分,就是这个现象所要教给他们的.这就是“题目”和“现象”带给学生的不同影响,也是二者的本质区别.唯有后者才提供了真正的教育,它给人的意识和行为带来了长久而稳定的改变.
4 用现象提供课程
课程天然地与“教育”连在一起,不能被用于教育的材料就不能说是课程.相应地,提供低效教育的就是低质量的课程,提供高效教育的就是高质量的课程.所以,《大辞典》不是课程,《百科全书》不是课程,《技术手册》不是课程.《教材》能不能成为高质量的课程,还要看教师们的二次开发.“用教材教而不是教教材”,也许是对这一意思的通俗表达.
为了证明此处的说法,请看案例2中接下去的教学活动:
(学生思考)
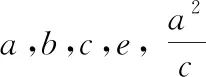
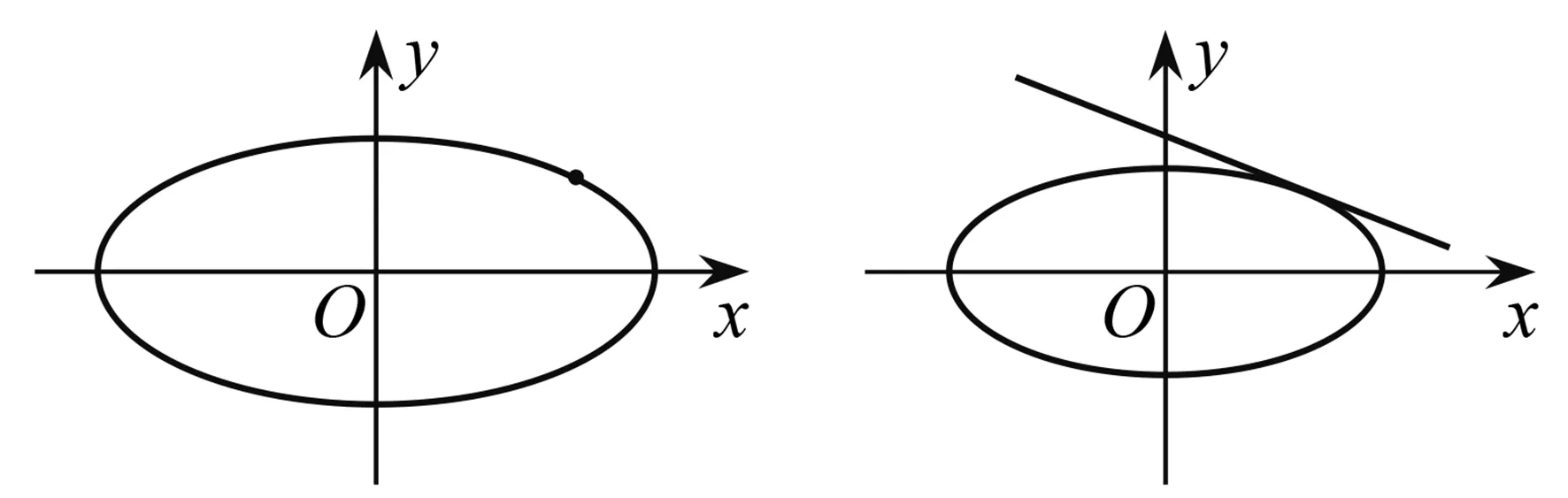
图2 图3
生:也可以给一个量再让椭圆和一条直线相切(图3).
生:还可以再让椭圆截一条直线所得弦长为已知数.
……
师生:啊?
生:比如知道椭圆上两个点的坐标……
这样的课程开发,学生似乎不是在学习解题,但却已经实实在在地能够解题.师生都渴望有超强的解题能力,而“超强的解题能力”必然是超越于题目之上的,若局限于题目之中就无法进入自由王国.
5 课程应该是问题串
把一道题目变成一个课程,必然要经过对题目的改造,而改造的手段究竟有多少,我们还不得而知(这是很有价值的研究课题).目前我们所掌握的主要是“问题串教学”,即用一连串不断推进或扩展的问题引领思维走向深入或开阔(就像前面的案例2),得到更本质的认识或更广泛的联系,单个的题目是不足以形成高效优质课程的.
这里要特别强调一点,那就是必须留意避免这样的错误:把“问题串”变成“任务串”.比如在一元二次方程判别式的教学中,给出一个未定的方程x2+3x+( )=0,然后现场在括号内填数,比如填上1, 5, 100, 2 018等,还可以“让学生决定填什么数”,一起来计算判别式的值是正的还是负的.每填一个数,学生只是去做道算术题,这样做看似热热闹闹实则是无所用心、不得要领.其实,我们只要改问“括号内填哪些数能使得方程有解?请你把所有这些数都找出来”,学习的形态就能大为改观,“任务串”也就恢复到了“问题串”.
问题串和任务串的差别在于前者引发思维、后者圈定范围.面对问题时,学生会主动开展猜想、试证、推翻、调整等,直至最后得出结论;面对任务时,学生会局限于任务本身,那是被动的、目标单一的活动.基于这个原因,笔者对“任务串教学”抱有警惕,对“任务群教学”抱有更大的警惕.我们平时见到的“任务群教学”提供的大多是一组没有逻辑结构的工作清单,连“任务串”的顺序性和递进性都失去了,那是“任务串”的混乱版、题海战术的加强版.有些地方干脆取了个“任务单教学”的名字,推广那种教学方式,这倒显得更直白、更实在(也更快速),当然也给我们带来了更大的不解和无奈.
为了形成对比,下面提供一个反面案例.
案例3函数单调性.
这个案例源于某一刊物,此处的讨论仅代表个人看法,欢迎批评指正.
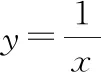
问题2在x轴上,从左到右自变量在增大,如何用数学符号反映?
问题3若自变量x在x1,x2处的值分别为f(x1),f(x2),那么当自变量在增大,引起函数增大(减小),如何用数学符号表示?
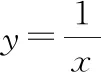
追问:由问题4可知,自变量任取两个值x1,x2,当x1
问题5结合上述问题的认识,你认为函数是递增的(或递减的),需要抓住那些关键因素?
问题6函数是递增的、递减的应该如何定义?
这里教师提供的问题多数不具有启发思维的功能而是任务布置,即使作为任务,也没有体现出逻辑递进关系.这从反面说明了讨论的必要性.
6 结语
韩愈在《师说》里讲到:“师之所存,道之所存.”教师怎样才能给学生以“道”?又能给他们怎样的道呢?“道可道,非常道”,这就给教师带来了极大的挑战.实际上,我们能给学生的都是具体的题目,但题目本身不是“道”,如果我们抱有“传道”的情怀,就必须去寻找一条切实可行的路径,本文的做法不妨一试.让有形的题目动起来,让它在不同的“形”之下显现出共同的“质”,如此则“道在其中矣”.“大道无形”,实乃因其形可变,具体的不变的“形”便显不出“道”的存在,这似乎是不言自明的.
变式教学被看做中国数学教育的最大特色,在世界上驰誉已久,这是我们自信心的源泉.“每道题目都是一个课程”,这一理念直接脱胎于变式教学,但是对它提出了一个新的目标或称原则.如何对待题目?“课程开发”的视角比“问题解决”的视角更具深度和广度,更利于落实核心素养教育,这是我们在现象教学实践中得到的一个体会,这个话题才刚刚开启.
