载人深潜器钛合金耐压球壳极限强度可靠性分析
2014-06-27,
,
(上海交通大学 海洋工程国家重点实验室,上海 200240)
目前全国产化的4 500 m载人深潜器正在研制中,将初步形成4 500 m水深的综合探查和作业能力。载人深潜器的耐压壳是保证潜水器正常工作和人员生命安全的重要结构构件,其设计的优劣直接关系到深潜器工作安全性和总体性能。对于工作深度大于800 m的载人潜水器,耐压壳基本采用球形结构[1]。目前大深度载人潜水器的耐压壳材料多选用钛合金,具有较高的比强度,并且在海水中抗腐蚀能力强。耐压球壳结构的极限强度和可靠性是评价深潜器安全性的重要指标,相关研究较多[2-6]。整体来看,国内外关于球壳极限强度的研究已有了一定的成果,但绝大多数局限于开孔或缺陷单独作用时的球壳极限强度,没有分析开孔、初始缺陷共同影响下极限强度的分布规律,也没有明确地给出可以用于工程设计参考的开孔球壳极限强度计算公式,并且分析中选取的变量较少、范围较小。为此,以全国产化4 500 m载人深潜器的研制为背景,结合国外载人深潜器下潜数据的统计资料,利用响应面方法对钛合金球壳的结构可靠性进行计算,分析了各随机变量的灵敏度。
1 钛合金耐压球壳极限强度的拟合
钛合金耐压球壳极限强度可靠性分析的关键之一在于获得耐压壳结构极限强度的表达式。完整球壳极限强度的经典理论公式适用于不考虑初始缺陷的情况,当需要考虑初始缺陷时,可采用数值分析方法将经典理论公式作为原型进行拟合。而实际耐压壳上存在开孔,则可进一步将完整球壳的拟合公式作为原型,拟合出考虑初始缺陷的开孔耐压球壳的极限强度表达式。
1.1 含初缺陷完整球壳极限强度的拟合公式
不考虑初始缺陷的球壳极限强度考虑的变量主要有球壳内半径R、厚度t,材料屈服强度σy,其经典公式为
(1)
式中:R——球壳内半径;
t——球壳厚度;
σy——材料的屈服强度。
根据计算,有限元计算结果与上述经典公式的计算结果之间保持线性关系,因此可以采用下式来表示完整球壳的极限强度。
(2)
初始缺陷有多种形式,为了简化分析,采用文献[4]中的缺陷模拟方法,考虑一阶弹性屈曲模态下的缺陷,见图1。
这种屈曲模态缺陷引入方式反映了最容易出现结构稳定性失效的形式,其中只需要初始缺陷幅值的一个参数即可表示整体缺陷情况,使分析更为快捷方便。
由于缺陷幅值Δ沿球壳径向分布,其与球壳中面半径的比值能够反映出缺陷相对于球壳的大小。此外,缺陷幅值的增加会引起球壳极限强度的降低,因此以上述完整球壳极限强度公式为原型进行修改,含初始缺陷幅值Δ的完整球壳极限强度基本表达式可以写成如下形式。

图1 初始缺陷示意
(3)
式中:a、b、c——待定系数;
Δ——初始缺陷幅值。
1.2 含初始缺陷开孔球壳极限强度的拟合公式
开孔球壳有多种结构形式,其开孔在一定程度上会对结构的极限承载能力产生影响。开孔球壳主要考虑的基本参数有开孔孔径Dk,开孔宽度bk,开孔加强处宽度bs,开孔连接处夹角θ、以及球壳厚度、内半径等,开孔处的封闭则以开孔处厚度tk来等效,见图2。

图2 开孔球壳结构示意
一般来说,潜水器耐压球壳开孔内径Dk以及开孔宽度bk都是由耐压球壳的布置要求确定的,因此在拟合公式中,不考虑这两项的变化,但在拟合公式的系数确定过程中,包含这两项的具体影响。
开孔连接处转角θ在耐压球壳设计过程中是一个重要的参数。为了分析θ对球壳极限强度的影响,保持球壳的半径、厚度、材料屈服强度不变,仅改变转角θ的大小。计算结果表明θ与极限强度之间基本呈线性关系,所以可以在完整球壳极限强度公式的基础上增加转角的线性项,表示转角对极限强度的影响。考虑开孔结构参数的影响,可以得到拟合公式:
(4)
如果进一步考虑初始缺陷的影响,则同样可以参考完整球壳极限强度的拟合公式(2),得到开孔球壳的极限强度拟合公式:
(5)
以上各式中a、b、c、d均为待定系数。
2 4 500 m HOV钛合金耐压壳的极限状态方程
2.1 极限强度表达式
分析对象为全国产4 500 m载人深潜器钛合金耐压球壳,该装置属于多开孔结构,设置了人员货物出入舱口、观察窗窗座等。球壳共有4个开孔,本文主要分析单开孔对球壳极限强度的影响,即分析开孔最大的人员出入孔。球壳开孔处内径Dk=480 mm,球壳开孔处宽度bk=60 mm,开孔处厚度tk为140 mm,主要考虑开孔加强处宽度、球壳开孔连接处转角、球壳内半径、球壳厚度等对结构极限强度的影响。球壳内半径考虑范围为950~1 050 mm,球壳厚度考虑范围为45~55 mm,加强处宽度考虑范围为100~200 mm,球壳开孔连接处转角范围为2.55~2.90 rad,初始缺陷范围为0~4 mm。
采用有限元方法计算含初始缺陷耐压球壳的极限强度,模型见图3。通过对模型计算时间和结果精度的综合考虑,有限元单元尺寸取为50 mm大小。

图3 开孔球壳有限元模型示意
4 500 m载人深潜器耐压球壳所采用的钛合金材料的弹性模量为115 GPa,泊松比为0.3,塑性本构关系见表1。

表1 钛合金材料塑性本构关系
通过批量的有限元计算之后,获得相应的计算结果(见图4、5)。利用拟合公式(5)进行拟合,最终得到含初缺陷开孔球壳的极限强度表达式为

(6)
经检验,相关系数R为0.995 2,相关系数平方和为0.990 4,决定系数DC为0.990 4,拟合的相关程度很高。
2.2 极限状态方程
对于载人深潜器耐压球壳可以建立如下抗力-载荷效应模型的极限状态方程:

图4 开孔球壳厚度半径比、开孔连接夹角与极限强度间关系

图5 不同初始缺陷下厚度半径比与极限强度间关系
式中:X1——球壳极限强度计算不确定系数;
X2——载荷不确定系数。
将式(6)代入到式(7)中,得到关于开孔球壳初始缺陷和开孔参数影响的极限状态方程。
G(R,t,σy,θ,X1,X2,Δ,P)=

(8)
利用式(8)的极限状态方程可以进行后续的结构可靠性分析。
3 极限强度可靠性计算与讨论
3.1 随机变量统计特性
参考图6中ALVIN号的下潜数据进行载荷分析,利用Gumbel分布函数进行拟合,拟合结果见图7所示,概率分布函数可以表示为
(9)

图6 ALVIN号下潜载荷谱

图7 Gumbel分布拟合结果图
再利用JC法[7]将非正态分布变量当量正态化,得到近似的正态分布函数的均值和变异系数。正态化后下潜深度的均值为2 408 m,变异系数为0.31。计算过程中考虑的参数还有球壳厚度t,球壳内半径R等,其统计特征值见表2[8]。
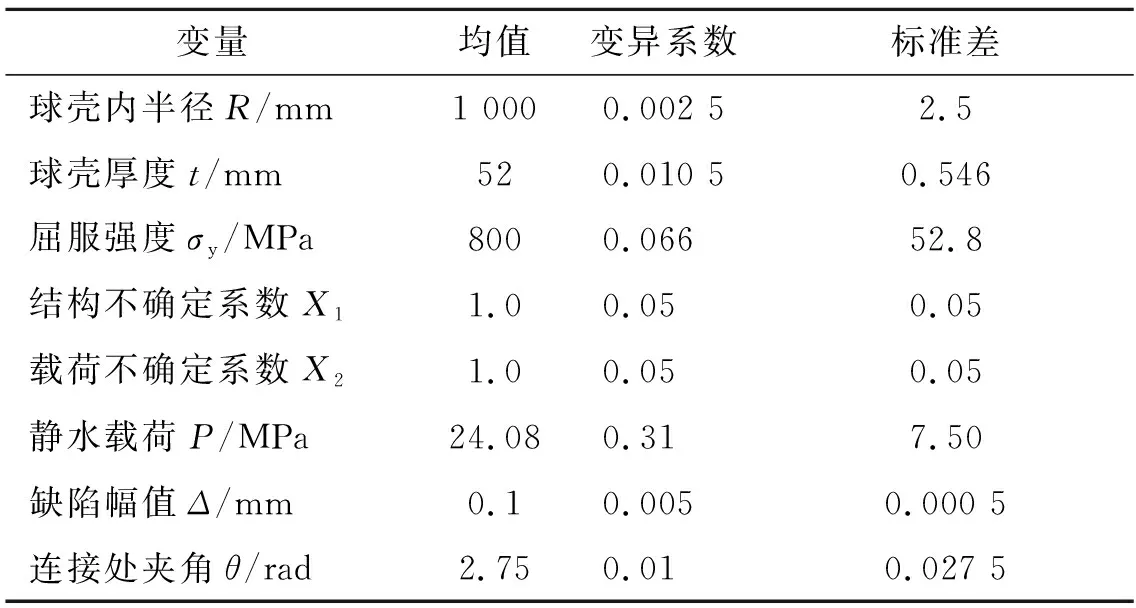
表2 钛合金耐压球壳基本变量的统计特性(均服从正态分布)
3.2 可靠性计算结果
采用改进一阶二次矩法对式(8)球壳极限强度可靠性指标β进行计算,迭代结果见表3。

表3 含初始缺陷4 500 m钛合金耐压壳可靠性指标计算结果
由迭代结果可以看出,在迭代第5次时可靠性指标最后收敛在5.379 5。参考《工程结构可靠性设计统一标准》[9]和《建筑架构可靠度设计统一标准》[10]设定目标可靠性指标应不小于4.2。因此可以认为初始缺陷影响下4 500 m载人深潜器钛合金开孔球壳结构极限强度可靠性是满足要求的,结构失效的概率较低。
3.3 随机变量对可靠性指标的影响
在潜水器耐压球壳极限强度可靠性强度计算中包含了许多随机变量,这些随机变量的概率分布以及变异系数对可靠性指标的计算会产生一定的影响,且影响程度不一。
针对式(8)结构极限状态方程分析各随机变量变异系数对可靠性指标的影响。各随机变量的影响程度,或极限强度可靠性对随机变量灵敏度,可以通过变量的变异系数变化0.001时可靠性指标的变动幅值来评价。不同参数变异系数改变0.001时的可靠性指标变化幅值计算结果见表4。

表4 变异系数改变0.001时可靠性指标变动幅值
各随机变量的影响程度由大到小排列为材料屈服强度σ,连接处夹角θ,结构极限强度计算不确定系数X1,载荷不确定系数X2,球壳厚度t,球壳内半径R,初始缺陷幅值Δ。各参数中影响最大的是材料的屈服强度,所以在考虑材料随机特性的情况下要尽量保证材料均匀一致,其屈服强度在一个稳定的范围内,进而提高球壳整体的安全性。连接处夹角θ对结构可靠性指标的影响较为明显,应该在设计的过程中考虑弧度角过渡。
4 结论
1)提出球壳极限强度拟合公式的原型,通过大批量的有限元分析得到考虑开孔和初始缺陷的极限强度拟合公式,对于不同的开孔球壳可以由该拟合公式为基础得到极限强度计算值。
2)基于极限强度拟合公式得到4 500 m载人深潜器钛合金球壳极限状态方程,可靠性指标计算表明,开孔和初始缺陷共同影响下钛合金球壳极限强度可靠性指标为5.38,满足目标可靠性要求,结构失效概率小。
3)通过可靠性指标计算分析了材料屈服强度、开孔连接处夹角、极限强度计算不确定系数、载荷不确定系数、球壳厚度、球壳内半径、初始缺陷幅值等参数的对球壳极限强度可靠性的影响程度,并对钛合金球壳的设计提出了建议。
[1] 施德培,李长春.潜水器结构强度[M].上海:上海交通大学出版社,1991.
[2] 陆 蓓,刘 涛,崔维成.深海载人潜水器耐压球壳极限强度研究[J].船舶力学,2004,8(1):51-58.
[3] 王仁华,俞铭华.初始缺陷对深海载人潜水器耐压球壳塑性稳定性影响[J].海洋工程,2005,23(4):111-115.
[4] PAN Binbin.An overview of buckling and ultimate strength of spherical pressure hull under external pressure[J].Marine Structures,2010,23:227-240.
[5] PAN B B,CUI W C,SHEN Y S.Experimental verification of the new ultimate strength equation of spherical pressure hulls[J].Marine Structures,2012,29:169-176.
[6] 陈承皓,薛鸿祥,唐文勇.基于全寿命扩展模型的钛合金球壳疲劳可靠性分析[J].上海交通大学学报,2013,47(2):307-311.
[7] 赵国藩.工程结构可靠度[M].北京:科学出版社,2011.
[8] 谢祚水,王自力.潜艇结构分析[M].武汉:华中科技大学出版社,2004.
[9] GB50153-2008.工程结构可靠性统一设计标准[S].北京:中华人民共和国建设部,2008.
[10] GB50068-2001.建筑结构可靠性统一设计标准[S].北京:中华人民共和国建设部,2001.
[11] 江晓俐.船舶结构极限强度可靠性分析方法研究[J].船海工程,2005(4):1-3.
