时间比对融合算法分析与比较∗

王威雄董绍武 武文俊 郭 栋张 健

(1中国科学院国家授时中心西安710600)(2中国科学院时间频率基准重点实验室西安710600)(3中国科学院大学天文与空间科学学院北京100049)

1 引言

高精度时间比对是实现国际原子时(International Atomic Time,TAI)和协调世界时(Coordinated Universal Time,UTC)的必要环节,卫星双向时间比对(Two-Way Satellite Time and Frequency Transfer,TWSTFT)和GPS精密单点定位(Precise Point Positioning,PPP)时间比对是目前精度较高的两种远距离时间比对手段,全球主要守时实验室一般都采用这两种手段参与TAI计算,且两者互为备份[1].TWSTFT的A类不确定度优于1 ns且长期稳定度较好,但其采样率较低且在长期比对过程中发现受到周日效应的影响.GPS PPP有优良的短期稳定度和高分辨率,但在实际比对结果中发现在日边界处会有明显不连续的“天跳”现象出现[2].2009年,国际计量局(Bureau International des Poids et Mesures,BIPM)的Jiang等人结合TWSTFT和GPS PPP长期和短期稳定度特性,通过Vondr´ak-ˇCepek组合滤波方法将GPS PPP和TWSTFT进行了融合,改善了TWSTFT的周日效应和比对链路的短期稳定度,并将其用于TAI的计算[3].

为提高时间比对链路的可靠性,BIPM鼓励采用多种方法对融合结果进行相互验证.因此,本文利用Kalman滤波算法首次将TWSTFT和GPS PPP两种独立而又互补的数据进行融合,并将结果分别与稳定度加权、Vondr´ak-ˇCepek组合滤波融合结果进行比较.由于目前德国物理技术研究院(Physikalisch-Technische Bundesanstalt,PTB)是全球时间比对网的中心节点,所以本文选取中国科学院国家授时中心(National Time Service Center,NTSC)和PTB间的欧亚链路一个月的实际比对数据进行分析.结果表明,3种融合算法对于TWSTFT中的周日效应以及GPS PPP结果的“天跳”现象都有不同程度的改善.

2 时间比对原理

2.1 卫星双向时间比对原理

卫星双向时间比对原理是利用地球同步卫星(Geosynchronous Earth Orbit,GEO)转发两个守时实验室的时间信号,如图1所示.将地面站1的时间信号由伪随机码(Pseudorandom Noise,PRN)信号调制到载波上,经甚小口径终端(Very Small Aperture Terminal,VSAT)发射到卫星,经卫星转发器转发到地面站2,地面站2接收经卫星转发的站1的时间信号,解调后与本地的主钟信号相比较,两站同时进行信号发射和接收,通过数据交换,扣除各项时延后就可解算出两地间的高精度钟差[4–5].

图1 卫星双向时间比对原理Fig.1 The principle of TWSTFT

站1和站2时间尺度间的差值计算公式为:

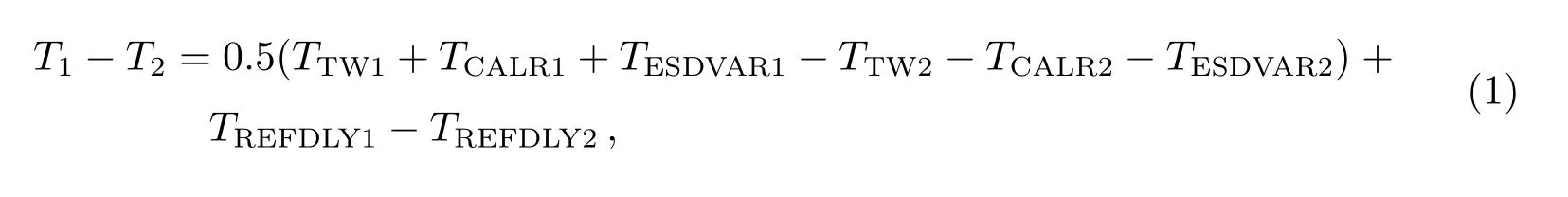
式中:Tk为本地时间尺度,k表示不同实验室1、2,下同;TTWk为本地实验室测得的信号到达时延;TCALRk为双向比对中的标定时延;TESDVARk为卫星双向链路标定后的地面站时延变化;TREFDLYk为本地时间参考点到双向设备的时延.

2.2 GPS PPP时间比对原理

GPS精密单点定位时间比对是利用国际GNSS服务中心(International GNSS Service,IGS)公布的GPS精密轨道和精密钟差数据,采用双频载波相位和伪距观测值计算得到本地接收机相对于参考时间IGS时(IGS Time,IGST)的钟差.在接收机经过校准后,该钟差可以看作本地参考时间(UTC(k))与参考时间IGST的偏差,两守时实验室通过GPS PPP的方法计算出本地时与参考时的钟差后,通过差分计算,即可得到两个实验室的时间比对结果,原理图如图2所示[6].

图2 GPS PPP时间比对原理Fig.2 The principle of GPS PPP time transfer

根据上述原理计算两时间实验室时间比对结果的公式为:

其中,∆Tutc1、∆Tutc2分别为参与比对的两个时间实验室的本地时间UTC(k)与参考时间IGST的偏差,Tutc1、Tutc2分别为两个时间实验室的本地时间.∆T1,2即为参与比对的两时间实验室的时间差.

3 数据融合方法

3.1 稳定度加权融合算法

依据各链路稳定度进行加权是时间比对融合中常用的方法,利用时间方差求得的稳定度越低,在融合计算中所占权重越小[7–8].因此权重与时间方差成反比,选择采样间隔为τ,权重设置如下:

其中和分别为TWSTFT和GPS PPP链路在采样间隔τ的时间方差,p1和p2分别为对应时间方差的倒数,ω1和ω2为相对应的权.为最大限度减小TWSTFT结果的周日效应,选取TWSTFT和GPS PPP在采样间隔τ=1 d的时间方差值计算权重.加权融合结果表示为:

式中Cn为融合结果,Tn为TWSTFT结果,Gn为GPS PPP时间比对结果,n为所用数据点数量.针对TWSTFT和GPS PPP时标不同的情况,采用3次样条插值的方法将两者时标对齐再参与计算.

3.2Vondr´ak-epek滤波融合算法

(1)曲线应该被平滑(最小化S);

(2)平滑值应该接近函数的观测值(最小化F);

(3)平滑曲线的一阶导数应该接近观测值的一阶导数值(最小化¯F).最小化以上约束条件可表示为:

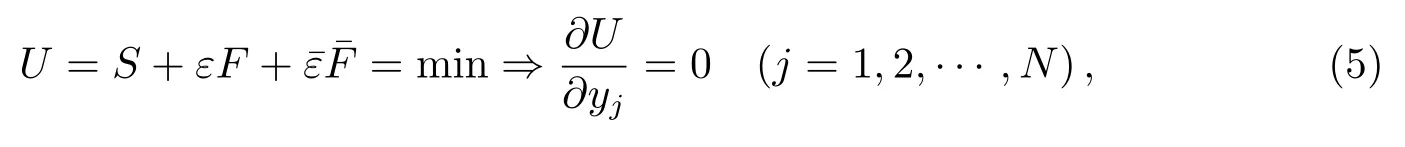
其中U为3种约束条件下的最小化结果,ε(>0)、¯ε(>0)分别是观测函数F和其一阶导数¯F的平滑因子,通过调节两个参数可以调节3种限制条件的均衡程度.平滑因子值越大,给定观测值或一阶导数的权越大,平滑后的值与观测值越接近.将TWSTFT结果作为观测值,将GPS PPP的一阶差分速率值作为一阶导数值对TWSTFT结果进行干预,以提高时间比对链路性能.平滑因子的选取通过频率响应法得到,这里频率响应为平滑数据的振幅与观测数据振幅之比,由于TWSTFT和GPS PPP融合目的是利用GPS PPP优良的短期稳定度来改善双向时间比对中的周日效应,因此对于需要抑制周日效应的TWSTFT数据我们取频率响应值为0.3,对于要充分利用的GPS PPP的一阶速率值,频率响应值取0.8,分别得到对应的平滑因子ε=26400、¯ε=6230,具体计算方法可参考文献[3].

3.3 Kalman滤波融合算法

Kalman滤波的每个递推周期中包含对被估计量的时间更新和测量更新两个过程.时间更新方程可视为预估过程,测量更新方程可视为校正方程[11–12].最后的估计算法成为一种具有数值解的预估-校正算法,假设离散时间过程由以下离散随机差分方程描述:

测量方程:

式中,Zm为m时刻对应的带噪声的测量变量,Xm为m时刻的估计状态变量;A为状态转移矩阵;Xm−1为过去m−1时刻的估计状态变量;B为控制矩阵;um−1为控制函数;wm−1为过程激励噪声;H为观测矩阵;vm为观测噪声.这里过程的状态不随时间变化,所以A=[1];B为双向时间比对的采样间隔的一半,B=[900];um−1为和双向时间比对对应时标相同的PPP速率值;包含噪声的观测值是状态变量的直接体现,所以H=[1].

随机信号wm和vm分别表示过程激励噪声和观测噪声.假设它们为相互独立、正态分布的白色噪声:

其中EQ和ER分别表示过程激励噪声协方差矩阵和观测噪声协方差矩阵.EQ=[Q],Q为过程激励噪声协方差矩阵系数.ER=[R],R为观测噪声协方差矩阵系数.通常,难以确定Q的值,因为我们无法直接观测到过程信号.一种方法是给定一个Q值,给过程信号“注入”足够的不确定性来建立一个可以接受的过程模型.

在TWSTFT和GPS PPP融合模型中,卡尔曼滤波输出的结果更多依赖于状态预测模型的精确性,因此应当给Q赋予一个较小的值,但在实际融合处理中,考虑到输入数据的不确定性以及递推过程中误差的不断积累,若Q的取值太小,数据融合后的结果会过度依赖状态预测模型的精确性,可能会导致滤波发散,因此本文取Q=0.00001.观测噪声协方差阵系数R为观测值卫星双向时间比对结果的噪声水平估计,本文取TWSTFT与GPS PPP作差结果的方差统计值作为观测噪声协方差阵系数值,经统计得R=0.5.

离散型卡尔曼滤波器的时间更新方程为:

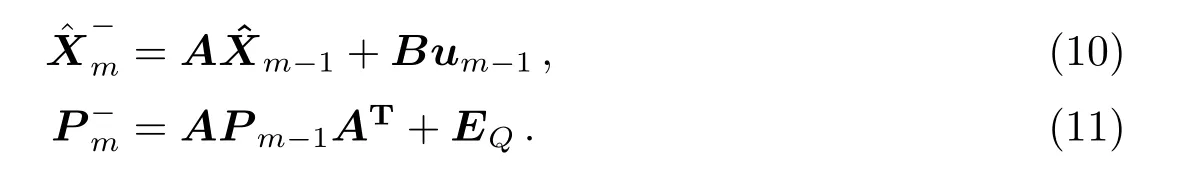
离散型卡尔曼滤波器的测量更新方程为:

Kalman滤波融合算法以TWSTFT数据为观测量,GPS PPP结果的一阶差分速率值作为Kalman滤波方程中的控制函数,利用融合算法来对Kalman滤波的预测过程进行修正,以提高滤波结果的可靠性.

4 结果与分析

选取基线长度约为7700km的NTSC-PTB链路2019年10—11月(MJD 58775—58804)TWSTFT和GPS PPP一个月的数据进行分析,参与比对的卫星双向时间比对系统和GPS PPP系统在两个实验室的参考同源且都为UTC(k).TWSTFT和GPS PPP比对结果如图3所示.

图3 TWSTFT和GPS PPP时间比对结果Fig.3 The results of TWSTFT and GPS PPP time transfer

从图3可以看出,TWSTFT结果与GPS PPP时间比对结果趋势一致,但在TWSTFT结果的某些天中有明显的周日效应存在,短期稳定度较差,在GPS PPP时间比对结果中也有明显的“跳变”现象出现.因此为提高时间比对链路性能,利用第3节的3种方法分别对TWSTFT和GPS PPP结果进行融合,融合结果如图4所示.

图4 不同方法融合结果Fig.4 The fusion results of di ff erent methods

从图4可以看出,3种不同融合方法的结果相近,对于TWSTFT中的周日效应以及GPS PPP结果的“天跳”现象都有不同程度的改善.Vondr´ak-ˇCepek融合结果的平滑程度更高,Kalman滤波融合和稳定度加权融合结果的平滑度虽然没有Vondr´ak-ˇCepek法的高,但它们能保留更多的原始比对信息.为对3种融合结果的一致性进行评估,我们以GPS PPP链路差值DCD结果为参考,分别计算其与3种不同融合方法结果的差,如图5所示,相关统计情况如表1所示.

图5 3种不同融合方法与GPS PPP DCD结果Fig.5 The DCD results of three methods against GPS PPP

表1 DCD结果统计Table 1 The statistics of DCD results

目前BIPM校准的GPS PPP链路的总不确定度为1.7 ns,从图5并结合表1可知,基于稳定度加权融合结果与GPS PPP的差值绝对值最大为0.95 ns,Vondr´ak-ˇCepek融合结果与GPS PPP的差值绝对值最大为1.18 ns,Kalman融合结果与GPS PPP的差值绝对值最大为1.34 ns,都在1.7 ns的不确定度范围内,说明3种方法融合的结果与GPS PPP结果有很好的一致性,可以满足国际时间比对要求.基于稳定度加权融合结果与GPS PPP DCD的标准差最小,因为PPP结果在权重计算中占有较大比重,Kalman融合结果和Vondr´ak-ˇCepek融合结果的均值和标准差相近,说明利用这两种方法的融合结果较为接近.为评价不同融合方法结果的稳定度,绘制不同方法相对应的时间偏差(TDEV)和修正Allan偏差(MDEV)如图6和图7所示.

从图6和图7可以看出,3种融合方法对于TWSTFT的短期稳定度和周日效应都有明显改善,3者1 d的时间和频率稳定度可以达到亚纳秒和10−15量级.在平均时间小于1 d时,由于Vondr´ak-ˇCepek融合的平滑性更强,其稳定度最高,但会丢失原始比对结果的固有信息,保真度较差;稳定度加权融合结果的保真度较好,但其主要是以牺牲PPP结果的短稳为代价,所以稳定度较差;Kalman滤波融合结果在不牺牲短期稳定度的同时,还具有很高的保真度,但在滤波初始化时收敛较慢.

图6 不同方法的时间偏差Fig.6 Time deviation of di ff erent methods

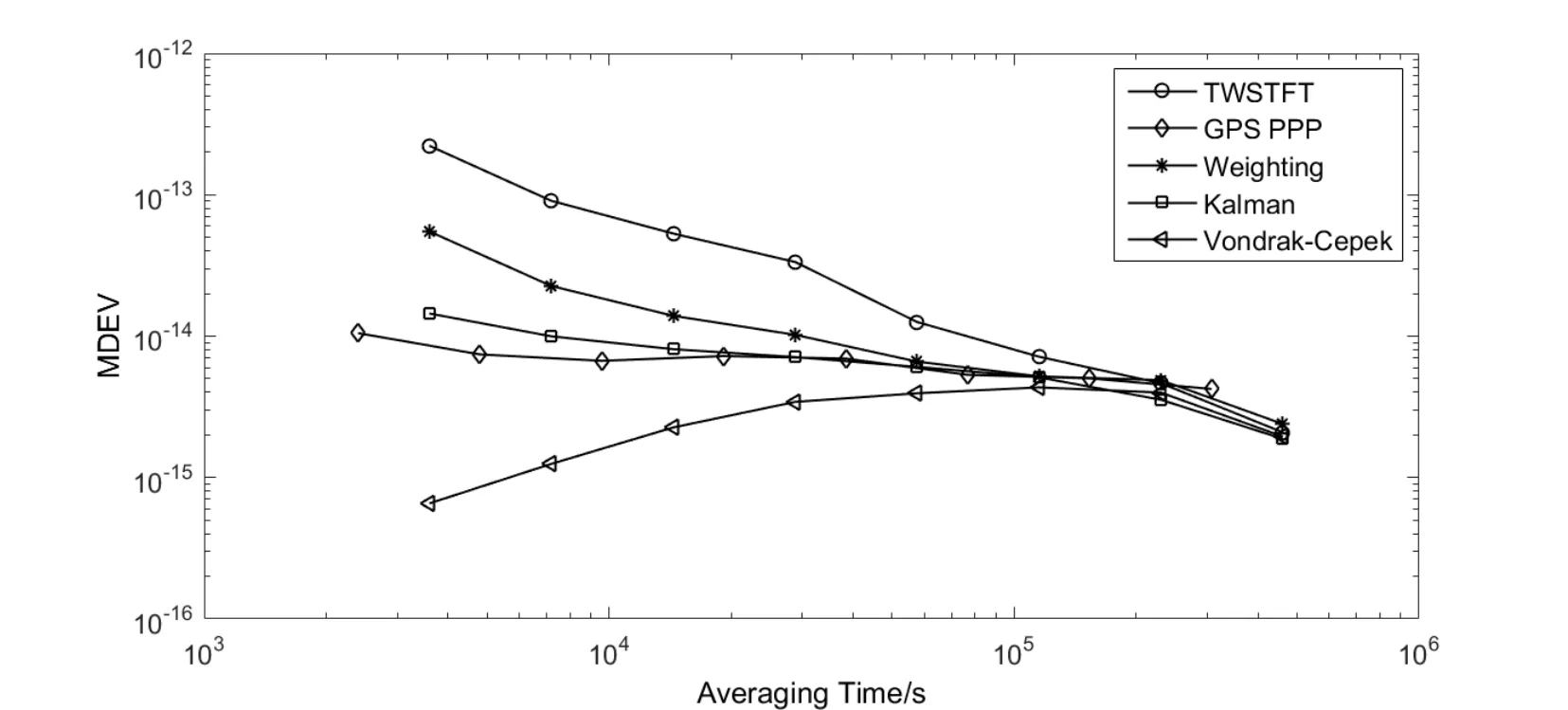
图7 不同方法的修正Allan偏差Fig.7 Modi fied Allan deviation of di ff erent methods

5 结论

本文首次实现了利用Kalman滤波的TWSTFT和GPS PPP融合,并与稳定度加权、Vondr´ak-ˇCepek滤波的融合结果进行对比,以DCD结果为参考,从时间偏差和修正Allan偏差等指标上对融合结果性能进行了评估.通过实测数据分析表明,3种融合算法都可提高时间比对链路的可靠性,对TWSTFT中的周日效应和GPS PPP的“天跳”问题有不同程度改善,且与GPS PPP的DCD结果在链路校准的不确定度范围内,符合当前国际时间比对精度要求.3者1 d的时间和频率稳定度分别可以达到亚纳秒和10−15量级.Vondr´ak-ˇCepek融合方法1 d以内的稳定度最高,保真度较差,适用于注重短期稳定度的时间比对链路融合.稳定度加权、Kalman滤波融合保真度较好,适用于对准确度要求高的时间比对链路融合,其中,稳定度加权融合计算简单、稳定度较差,Kalman滤波融合稳定度较高,但其计算过程复杂,可根据实际中不同时间比对要求选取不同的融合算法.