遗传算法优化的BP神经网络卫星钟差预报∗

孙鹏超 魏东平 孙碧娟

(1中国科学院大学地球与行星科学学院北京100049)(2西安邮电大学通信与信息工程学院西安710061)

1 引言

北斗卫星导航系统(BeiDou navigation satellite system,BDS)是中国自主实施研发,独立运行的卫星导航定位系统.在利用全球导航定位系统(Global Navigation Satellite System,GNSS)导航、定位和授时的过程中,时间同步技术在一定程度对结果的精度起着决定性的作用.时间同步技术中,对于卫星钟参数的合理估计以及钟差的预报研究是关键点[1].这就需要我们通过对卫星钟的运行性能分析,建立一种实时高精度的卫星钟差预报模型.

目前,许多学者在卫星钟差预报方面进行了深入研究,提出了很多高精度钟差预报模型.其中常见的模型主要有:灰色模型(GM(1,1))、序贯二次多项式模型、时间序列模型、卡尔曼滤波模型和神经网络模型等[2].文献[3]通过二次多项式、灰色模型和线性组合模型对BDS钟差预报,结果表明随拟合时长增加,预报精度逐步提高且趋于稳定.文献[4]提出附加周期和神经网络补偿的实时钟差预报模型,获取的BDS超快速钟差产品相比德国地学中心超快速钟差产品和国内iGMAS(International GNSS Monitoring&Assessment System)超快速钟差产品精度均有较大提升.文献[5]将神经网络模型应用于卫星钟差短期预报,预测结果可以为实时GPS动态精密单点定位提供服务,但是神经网络模型容易陷入局部最小,导致预报结果的精度难以满足要求.文献[6]用灰色模型和神经网络的混合模型进行钟差预报,实验显示该模型优于经典加权方法的线性组合灰色模型.文献[7]提出一种基于指数平滑法的GPS卫星钟差预报方法,利用少量数据建模且计算结果优于二次多项式,与灰色模型精度相当.

星载原子钟的时频特性复杂且极易受外部环境的影响[4],研究表明原子钟钟差变化整体的趋势项是一个二次多项式,剩余部分是周期项.因此我们得到的卫星钟差数据通常具有非线性和周期性变化的特点.BP(Back Propagation)神经网络具有较强非线性映射能力,无需依据严密的数学方程进行推算.相比常规预报模型处理非线性无规律误差,BP神经网络可以通过对大量非线性钟差数据的学习来建立映射关系并进行钟差的预报.通常我们采用“滑动窗”[8]划分数据,输入层为钟差数据序列前T个时刻值,目标输出层为第T+1个值,权值是输入层到隐含层以及隐含层到输出层连接的权值,阈值为隐含层每个神经元的值.BP神经网络的训练是不断修正权值和阈值使得输出误差不断减小的过程,但容易陷入局部极小,是一种局部搜索的最优化方法,无法达到全局最优.为此针对BP神经网络卫星钟差预报模型建立过程中输入层、隐含层和输出层权值和阈值的全局最优化问题,提出了遗传算法(Genetic Algorithm,GA)优化的BP神经网络模型(GA-BP),通过寻求BP神经网络模型在预报过程中全局最优权值和阈值,进一步提高BP神经网络卫星钟差短期预报的精度.

2 遗传算法优化BP神经网络

BP神经网络是一种有效的多层神经网络学习方法,其主要特点是信号前向传递,而误差后向传播,通过不断调节网络权值,使得网络的最终输出与期望输出尽可能接近,以达到训练的目的[9].在算法实现中这个调节的过程是反复进行的,直到网络最终的输出结果的误差小于预设定的误差精度或是达到设定的迭代次数.BP神经网络是由输入层、隐含层和输出层组成的.BP神经网络也具有局限性,如对初始权值十分敏感,容易陷入局部最优.

图1为BP神经网络的拓扑结构,其中输入层神经元个数为n,p1,p2,···,pn为输入值,隐含层神经元个数为m,激活函数为f1,输出层神经元个数为l,a21,a22,···,a2l为输出值,激活函数为f2,wij为第j个输入层神经元与第i个隐含层神经元的连接权值,wki为第i个隐含层神经元与第k个输出层神经元的连接权值[10].

图1 BP神经网络的拓扑结构Fig.1 The topology of BP neural network

本文在建立BP神经网络模型预报钟差时,隐含层神经元个数m根据经验公式:

确定.式中,α为1–10之间的常数.

隐含层中第i个神经元的输出为:

其中,a1i表示输入钟差值经隐含层计算输出的值;b1i表示隐含层各神经元的阈值.输出层第k个神经元的输出为:

其中,a2k表示预测的钟差值;b2k表示输出层各神经元的阈值.

遗传算法是一种进化算法,其基本原理是效仿自然界的“物竞天择,适者生存”的演化法则,进行每代的选择、交叉重组和变异,直至种群逐渐趋于平衡态,即遗传过程中那些具备相对优势的特征被极大地保留,劣势的特征趋于消失的结果.遗传算法是一种自适应性全局搜索最优解的迭代算法,不依赖梯度信息,具有良好的并行性和鲁棒性,能进一步提高算法效率[11].

遗传算法优化BP神经网络的思想就是遗传算法在目标信息的解空间进行综合性的搜索,BP算法在遗传算法搜索到一个比较优的网络形式时进行定位,寻找到问题需求的最优解[11].遗传算法优化BP神经网络的过程主要包括:(1)确定要建立的BP神经网络的结构;(2)根据训练数据利用遗传算法优化建立的BP神经网络模型的权值和阈值;(3)将优化后的权值和阀值赋予BP神经网络模型进行预测,如图2所示.基于遗传算法优化BP神经网络的步骤如下[11–12]:

(1)确定BP神经网络的拓扑结构.根据文中所提及的“滑动窗”思想和隐含层确定方法,我们确定输入层神经元(输入钟差数据)个数为15、隐含层神经元个数为6、输出层神经元(输出钟差数据)个数为1;

(2)对BP神经网络的权值和阈值进行编码.根据BP神经网络数据为[−1,1]之间的小数且数量巨大的特点,我们采用实数编码规则,得到初始种群;

(3)适应度函数为f(C)=1/C.用个体代表神经网络初始的权值和阈值,利用个体初始化BP神经网络进行钟差预测,将预测输出值和实际输出值的误差绝对值作为适应度函数变量值C,并判断是否满足优化的标准,若符合则进入步骤(4),否则剔除此个体;

(4)选择满足适应度要求的个体,进行复制、交叉以及变异产生新的个体.具体操作方法如下[13]:

复制操作采用轮盘赌的选择方法,选择概率Pu由下式决定:

其中,Xu为第u个个体;N为总个体数.将当前群体中适应度高的个体完整复制到下一代中.

图2 遗传算法优化BP神经网络的流程图Fig.2 Flow chart of BP neural network optimized by genetic algorithm

交叉操作中个体的编码方式为实数编码,因此交叉采用实数交叉法[14],具体的计算方式为:

其中,vxt、vyt分别为第x和第y个基因的第t位;β为[0,1]之间的随机数.

变异操作的方式为:

其中,vmax、vmin分别为基因vzt取值的上、下界;r为[0,1]上的随机数;r0为随机数;g为当前迭代次数;Gmax为最大进化代数.

(5)查看产生的新个体是否满足最优个体的标准,若是满足则继续进行下一步骤,若不满足,则返回到步骤(2);

(6)将最终获取的最优个体进行解码,分别作为BP神经网络的权值和阈值;

(7)建立BP神经网络模型,计算全局误差,反向调整网络中的参数,重复迭代训练,直至达到误差精度要求或迭代次数上限;

(8)使用遗传算法优化后的BP神经网络模型进行钟差预报.

3 算例与数据分析

为了验证本文方法的效果,采用德国地学研究中心(GFZ)提供的采样间隔为5 min的事后精密钟差数据进行建模分析.选取3种类型不同的北斗卫星钟差数据,我们以C03(Geosynchronous Orbit,GEO)、 C08(Inclined Geosynchronous Orbit,IGSO)和C11(Medium Earth Orbit,MEO)号卫星为代表,分别进行模型建立以及钟差预报.

3.1 数据预处理

卫星钟差原始数据通常为相位数据,数值大于其频率数据,粗差往往隐藏于钟差序列中不利于粗差探测,导致钟差数据质量伪高.当将相位数据转化为频率数据时,钟差数据值会缩小,但粗差值相对于频率数据集会放大[15].因此可以有效地发现其中的粗差,进而提高数据的质量.卫星钟差数据与频率数据之间的转换关系如下:

式中,Is+1为第s+1个历元对应的相位数据;Is为第s个历元对应的相位数据;Ys为第s个相位数据对应的频率数据;∆t为采样间隔.

图3–5分别是本次实验卫星C03、C08与C11所对应的钟差相位数据和频率数据.

从图3–5的图(a)中可以看出,卫星钟差的相位数据为线性,没有明显的不连续点位或者突兀点位.图3–5的图(b)为钟差频率数据,通常为了提高数据模型的可靠性和预报精度,需要对其中的粗差进行探测并剔除.

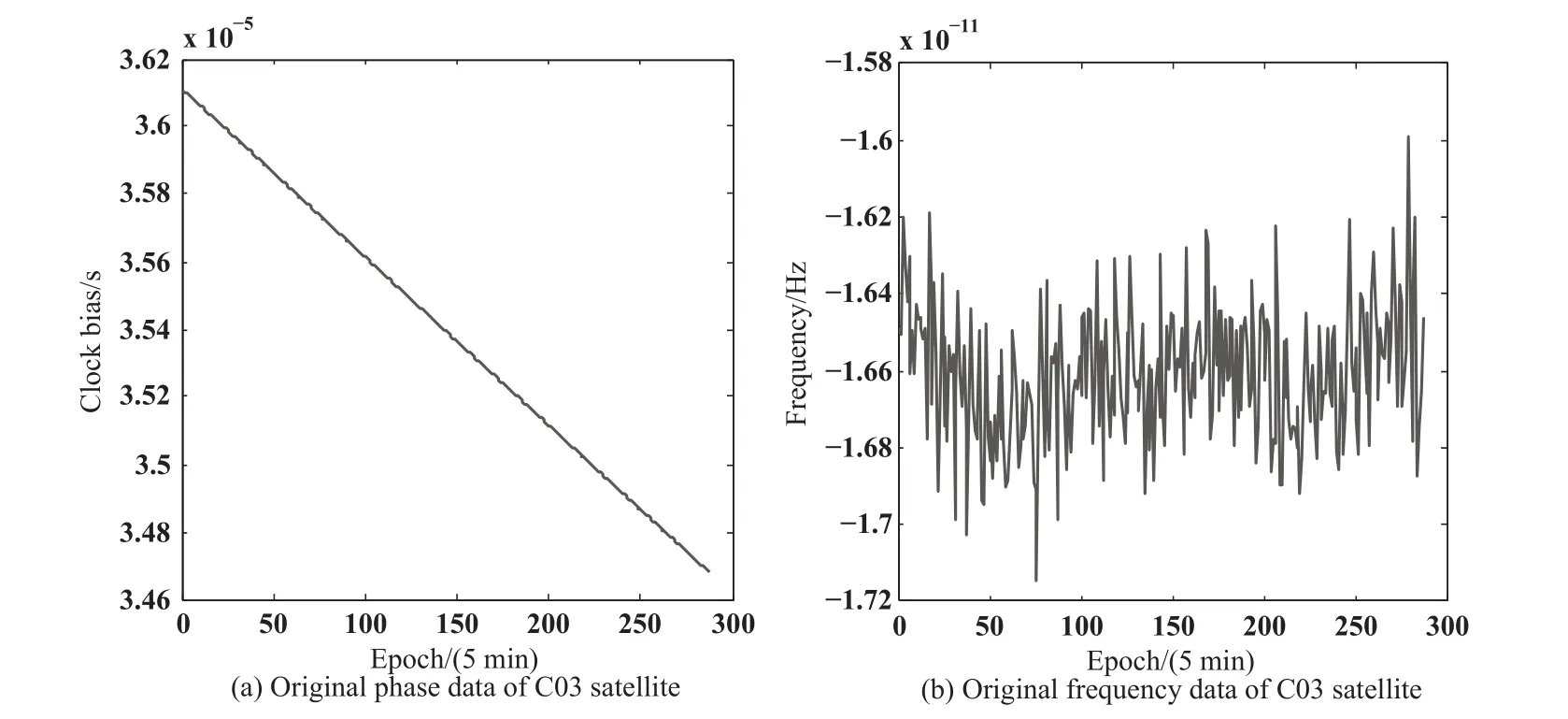
图3 C03卫星钟差数据Fig.3 Clock bias data of C03 satellite

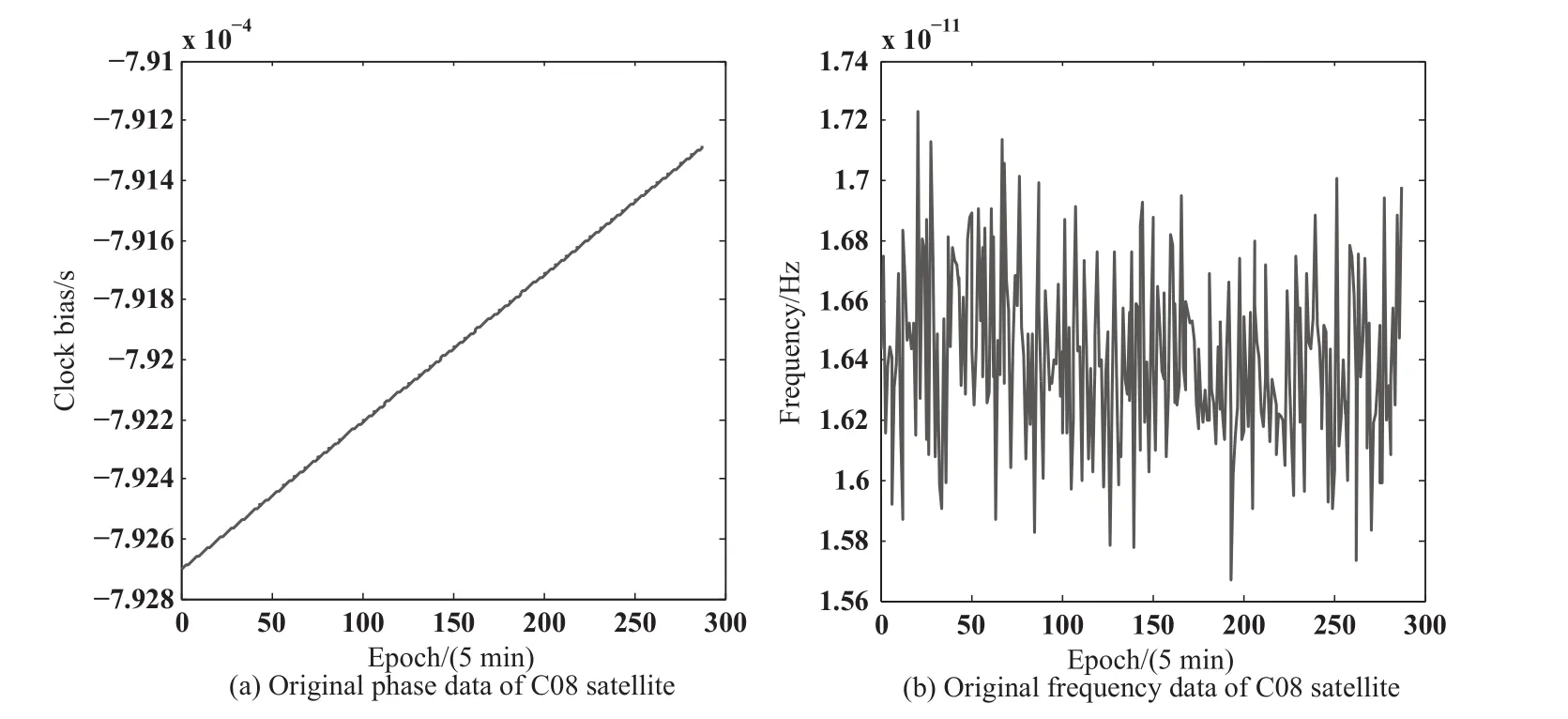
图4 C08卫星钟差数据Fig.4 Clock bias data of C08 satellite

图5 C11卫星钟差数据Fig.5 Clock bias data of C11 satellite

本文采用常用的粗差探测方法—中位数粗差探测法,其具体的表达式如下[12]:

式中,median为中位数运算符;M为频率数据的中位数;P为实际情况下所确定的正整数;MAD为频率序列偏差绝对值的中位数.

从(9)–(10)式可以看出,当频率值大于其中位数M和P倍频率序列偏差绝对值的中位数之和时,我们便判定其为粗差,并将粗差值剔除.同时利用拉格朗日插值对缺失数据点插值,以保证数据在处理后的完整性.通过实验我们确定P为4,经测试此次选取的卫星钟差数据并未存在明显的粗差,故不需要进行插值流程.

本文选取均方根误差(root mean square error,RMSE)作为评价模型预报精度好坏的依据,其中均方根误差计算的公式如下[16–18]:

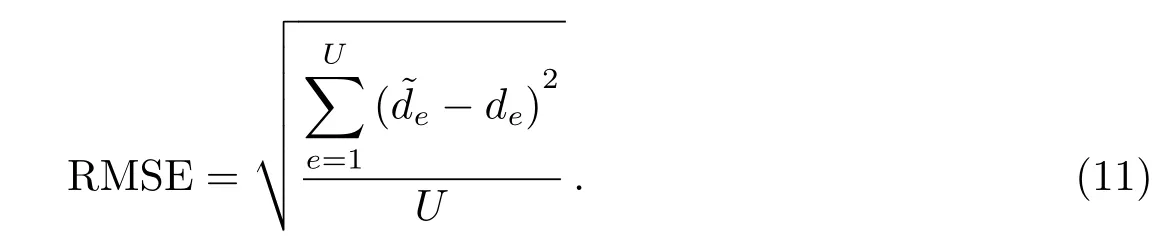
3.2 预报结果及精度分析

分别选取2015年4月4日24 h共288组数进行遗传算法优化的BP神经网络模型建模,并对4月5日1 h、3 h以及6 h的钟差进行预测,同时利用相同数据进行GM(1,1)模型、BP神经网络的建模以及相同时间段钟差预测,对比3种模型预报结果的优越性.

利用数据进行3种模型的建模得到C03、C08和C11卫星钟差的各个模型预测值和GFZ发布的事后精密钟差值(可以视作真值)的离散程度如图6–8所示.

图6 C03卫星钟差预测值和真值离散程度Fig.6 Dispersion of predicted and true values of C03 satellite clock bias

图7 C08卫星钟差预测值和真值离散程度Fig.7 Dispersion of predicted and true values of C08 satellite clock bias

通过计算各个时段预报值与真值的差值,我们可以得到相应的预报误差折线如图9–11所示,同时我们根据误差值计算出不同时间段的均方根误差如表1所示.

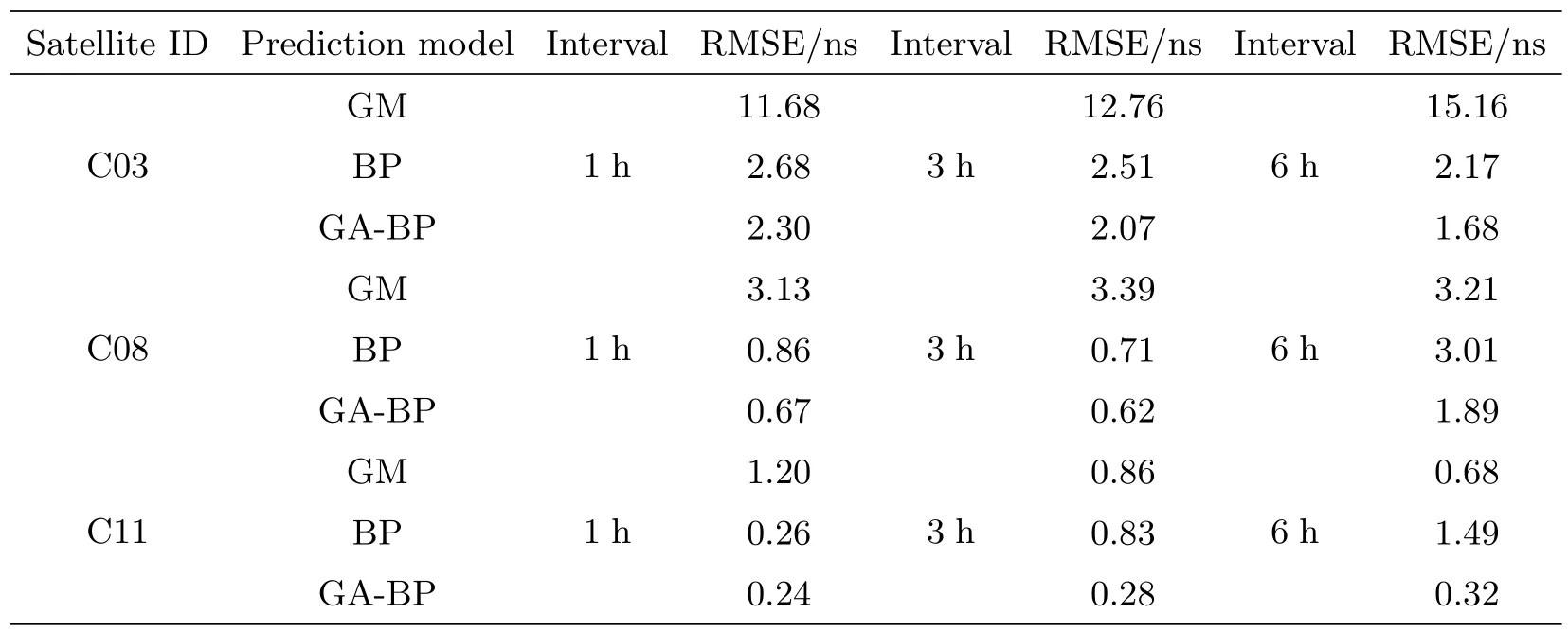
表1 卫星钟差预报误差统计Table 1 Statistics of satellite clock bias prediction errors

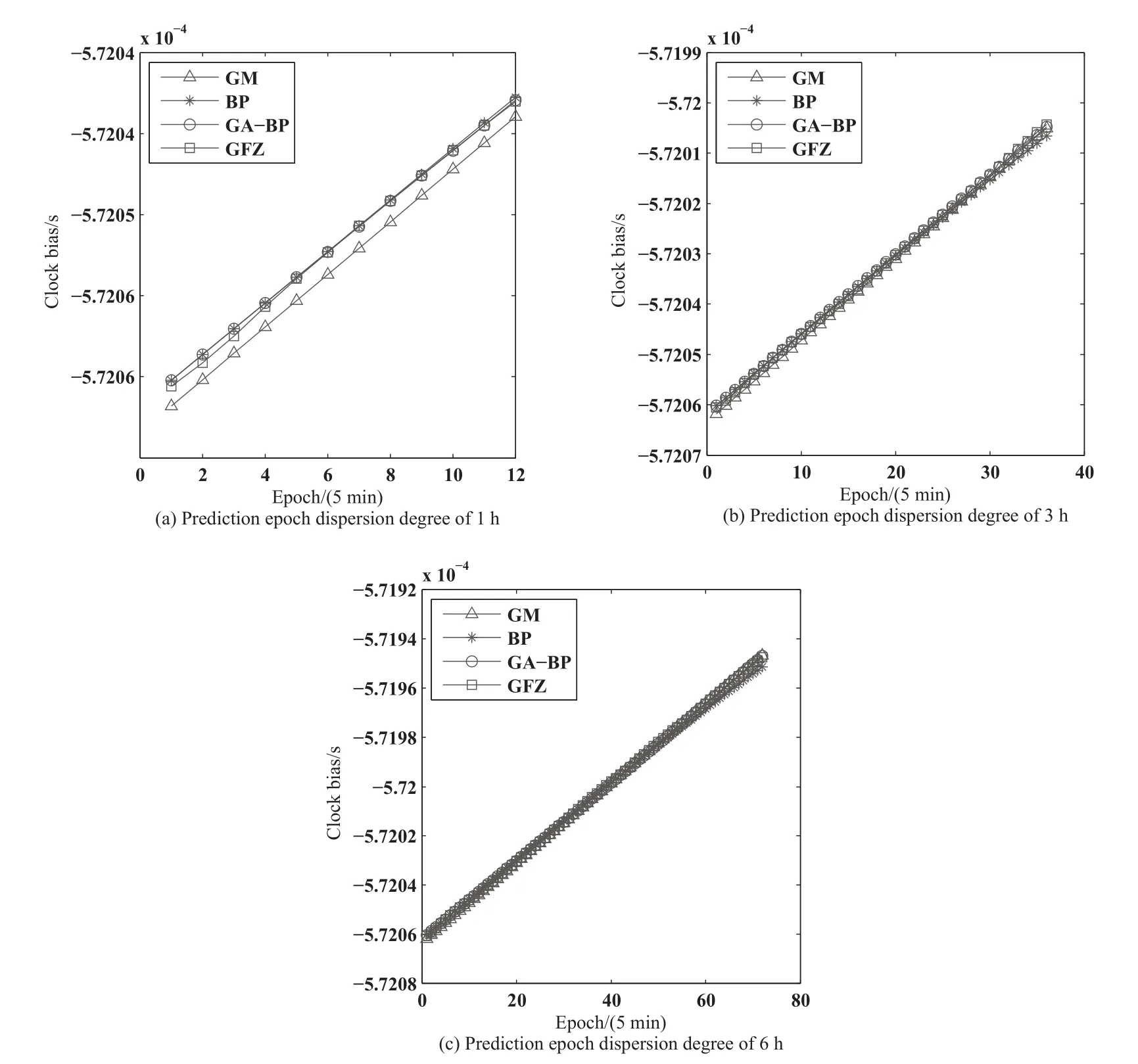
图8 C11卫星钟差预测值和真值离散程度Fig.8 Dispersion of predicted and true values of C11 satellite clock bias

结合图6–11以及表1分析:

(1)对C03号卫星分析,图6中GM(1,1)模型、BP神经网络模型以及GA-BP神经网络预报结果对比,我们可以看出GM(1,1)模型预报值较真值的偏离程度较大,BP神经网络模型以和GA-BP神经网络预报结果和真值比较接近.图9为预报误差,从中我们可以看出GM(1,1)模型在起始历元的预报中相对于BP神经网络和GA-BP神经网络的预报精度表现出极大的误差.随着预报历元的增长,GM(1,1)的均方根误差随着时间不断扩大.反观BP神经网络和GA-BP神经网络,预报误差则呈现出减小的趋势,精度远远优于GM(1,1).可能是从GEO卫星获取的钟差数据质量不高,使得GM(1,1)模型累加得到的时间序列并不够光滑,因此导致建模过程中确定的参数未能很好表现出原数据序列的变化趋势.GA-BP神经网络模型预测的结果在相同预报时段精度优于BP神经网络,说明使用遗传算法对BP神经网络权值和阈值优化后,钟差数据的预报精度有所提高;

图9 C03卫星钟差预报误差图Fig.9 Prediction error of C03 satellite clock bias

(2)从C08卫星钟差的预报结果,我们可以看出GM(1,1)模型、BP神经网络模型和GA-BP神经网络模型均方根误差总体趋势为随着预测历元的增加逐渐增大.BP神经网络和GA-BP神经网络在前3 h内精度可达到亚纳秒级,GM(1,1)模型则误差在3–3.5 ns范围内.GA-BP神经网络、GM(1,1)预报误差呈减小趋势,BP神经网络的预报误差曲线则呈现较大变化且整体趋势呈现增大,说明遗传算法对BP神经网络在一定程度上进行了优化并提高了精度.从整体看GA-BP神经网络模型精度均优于其他两种模型;

(3)对于C11卫星钟差的预报,3种模型的预报精度处于或接近亚纳秒,可以看出C11卫星的钟差数据精度比较高,在建模过程中各个参数的求解精度较好.其中GM(1,1)模型的预报均方根误差呈现减小趋势,猜想GM(1,1)在中长期的钟差预报中可能具有较好的精度.在钟差预报中GA-BP神经网络预报误差整体表现平稳,相比GM(1,1)和BP神经网络模型在预报精度上总体较好;

图10 C08卫星钟差预报误差图Fig.10 Prediction error of C08 satellite clock bias

(4)通过图9(a)、(b),图10(a)、(b)和(c)以及图11(a)、(b)的对比,我们发现GA-BP神经网络和BP神经网络模型预报误差的总体变化趋势相近,但GA-BP神经网络模型较为平稳,说明BP神经网络的初始参数对遗传算法的优化趋势有一定的影响,因此初始值选取是否合适对于遗传算法搜索BP神经网络权值和阈值最优值、提高模型钟差预测的精度有很大影响;

(5)在图9(c)和图11(c)中,对比BP神经网络和GA-BP神经网络的预报误差曲线图,我们可以看出当BP神经网络预测出现较大误差时,经过遗传算法优化后能够在一定程度改变误差的大小和变化方向,有效地保证预报的精度.

图11 C11卫星钟差预报误差图Fig.11 Prediction error of C11 satellite clock bias

4 总结

本文提出遗传算法优化的BP神经网络卫星钟差预报模型,为利用BP神经网络进行钟差预报过程中权值和阈值的最优化问题提供了一种解决方法.利用优化后的BP神经网络对BDS钟差进行短期预报,结果显示其精度优于BP神经网络和GM(1,1)模型,说明了遗传算法优化BP神经网络进行钟差预报的可行性和有效性.但优化模型未用于中长期钟差的预报,所以应用于中长期预报的可行性有待验证.文中BP神经网络钟差预报模型在数据训练过程中初始权值和阀值均采用随机生成,但实验过程发现BP神经网络初始值对于模型优化具有影响,因此还需探究如何合理选取初值,进一步提高优化模型的预报精度.

致谢感谢审稿专家和编辑老师对文章提出问题和给予宝贵的建议.感谢德国地学中心提供的BDS卫星精密钟差产品数据.